特殊结论 与 思维
Tom17
·
·
个人记录
目录
-
遇到二选一,或者某种互斥关系的,一般考虑建图。
-
斯特林数与 NTT
-
某一个变量范围比较小,然后又是求类似交/并的,考虑容斥反演。
-
遇到一些需要动态开点线段树的题目,考虑是否可以先进行离散化。
-
曼哈顿转切比雪夫:(x,y) 映射到 (x+y,x-y) 那么则有 |x_A-x_B|+|y_A-y_B| 转为 \max(|x_A-x_B|,|y_A-y_B|)。
-
树链剖分相关的题目,建议将重心定为根,这样可以减少常数。
-
对拍去重
-
多端点定序枚举问题的优化
-
差分转换
-
计数转概率/转期望
-
图论问题/排列问题和基环树森林
-
树上选路径问题的思路
-
指数分治
-
排列枚举 (x!!=x(x-2)(x-4)\cdots)
-
三维偏序转二位偏序
-
加和字符串偏序
-
线性基异或和为 x 的方案数
-
一个 01 序列相邻删除相同/不同元素
-
若干个单调性询问考虑转二分为扫描线
-
树上问题一个点是否为另一个点的祖先
-
二项式定理:(a+b)^n=\sum_{i=0}^{n}\binom{n}{i}a^ib^{n-i}。
-
Kruskal 重构树
-
点覆盖区间模型
-
Ad-hoc 计数题中的 DP 状态优化
-
随机化技巧和骗分
-
数据结构维护,考虑独立的操作能否分别维护
-
把 n 个物品分成若干份,每份为 d 或 d+1,那么合法 d 数量为 O(\sqrt n) 级别
-
把一个有向图添加一个虚点和一些边,使其变为欧拉回路图,添加最少边数的方案是,把每个点入度和出度补成相等(不考虑连通性)
-
快速变换:对于不能直接操作点积的变换快速幂,可以考虑采用朴素分治快速幂。
-
当打表发现有一些数列类似于组合数的行,但是不像,且中间有若干个数相同,且是 2 的幂次,要注意其是否是组合数平移若干个相加的结果。
-
条件概率
-
系数倒推的技巧
-
区间连通块/区间生成树问题,考虑扫描线并用 \min(u,v) 为权值,用 LCT 维护最大生成树
-
模意义下高斯消元和行列式计算
正文
1. 遇到二选一,或者某种互斥关系的,一般考虑建图。
- BSOI 13304 【8.11NOIP模拟】旋转 对向格子必须一边放,一边不放。
- BSOI 13319 【8.15NOIP测试】整数二元组 每对数必须选其中一个,不选另一个。
2. 斯特林数与 NTT
- BSOI 13320 【8.15NOIP测试】序列修改 中的 \sum_{d=0}^m(-1)^d\binom{m}{d}(m-d)^q 在 q<m 时为 0。
待补 NTT 求斯特林数结论。
第二类斯特林数表:
| n |
n\brace 0 |
n\brace 1 |
n\brace 2 |
n\brace 3 |
n\brace 4 |
n\brace 5 |
n\brace 6 |
n\brace 7 |
n\brace 8 |
n\brace 9 |
| 0 |
1 |
|
|
|
|
|
|
|
|
|
| 1 |
0 |
1 |
|
|
|
|
|
|
|
|
| 2 |
0 |
1 |
1 |
|
|
|
|
|
|
|
| 3 |
0 |
1 |
3 |
1 |
|
|
|
|
|
|
| 4 |
0 |
1 |
7 |
6 |
1 |
|
|
|
|
|
| 5 |
0 |
1 |
15 |
25 |
10 |
1 |
|
|
|
|
| 6 |
0 |
1 |
31 |
90 |
65 |
15 |
1 |
|
|
|
| 7 |
0 |
1 |
63 |
301 |
350 |
140 |
21 |
1 |
|
|
| 8 |
0 |
1 |
127 |
966 |
1701 |
1050 |
266 |
28 |
1 |
|
| 9 |
0 |
1 |
255 |
3025 |
7770 |
6951 |
2646 |
462 |
36 |
1 |
第二类斯特林数表乘 m!:
| n |
n\brace 0 |
n\brace 1 |
n\brace 2 |
n\brace 3 |
n\brace 4 |
n\brace 5 |
n\brace 6 |
| 0 |
1 |
|
|
|
|
|
|
|
|
|
| 1 |
0 |
1 |
|
|
|
|
|
|
|
|
| 2 |
0 |
1 |
2 |
|
|
|
|
|
|
|
| 3 |
0 |
1 |
6 |
6 |
|
|
|
|
|
|
| 4 |
0 |
1 |
14 |
36 |
24 |
|
|
|
|
|
| 5 |
0 |
1 |
30 |
150 |
240 |
120 |
|
|
|
|
| 6 |
0 |
1 |
62 |
540 |
1560 |
1800 |
720 |
|
|
|
观察技巧:
第二类斯特林也要背,有一道例题:
[【51nod】 1229 序列求和 V2](https://vjudge.net/problem/51Nod-1229/origin) / [P4948 数列求和](https://www.luogu.com.cn/problem/P4948)
> 给定 $n,k,r$,求
> $$
> \sum_{i=1}^n i^kx^i
> $$
>
> (范围:$1\le n,r\le 10^{18},1\le x\le 2000$)
>
> 直接做不是很好做。从边界入手,注意 $k$ 是可以枚举的,我们考虑思考 $k=0$、$k=1$ 和 $k=2$ 的情况。
>
> $k=0$ 是等比数列求和。
>
> $k=1$ 是系数为等差的等比数列求和。发现这个差分一下就可以得到与 $k=0$ 相似的式子。
>
> $k=2$ 比较难,因为差分之后不是很相似。
>
> 考虑倒着来。我们将 $k=1$ 时的数组前缀和得到类似 $k=2$ 的式子,不断可以得到 $F_k$ 的式子。系数如:
>
>
> ||$x^1$|$x^2$|$x^3$|$x^4$|$x^5$|$x^6$|
> |:-:|:-:|:-:|:-:|:-:|:-:|:-:|
> |$F_0$| $1$ | $1$ | $1$ | $1$ | $1$ | $1$ |
> | $F_1$| $1$ | $2$ | $3$ | $4$ |$5$| $6$ |
> | $F_2$| $1$ | $3$ | $6$ | $10$ | $15$ | $21$ |
> | $F_3$| $1$ | $4$ | $10$ | $20$ | $35$ | $56$ |
> | $F_4$| $1$ | $5$ | $15$ | $35$ | $70$ | $126$ |
> | $F_5$| $1$ | $6$ | $21$ | $56$ | $126$ | $252$ |
>
> ($F_k$ 均为无穷项多项式。)
>
> 有 $[x^p] F_q=\binom{p+q-1}{p-1}$。
>
> 考虑用 $F(0)\sim F(k)$ 来表示 $S(k)=\sum_{i=1}^{\infty} i^kx^i$。
>
> 则有
>
> $$
> S(k)= \sum_{i=0} {k \brace i} i!(-1)^{k-i} F(i)
> $$
>
> 可见,组合数多项式和方幂多项式可以通过斯特林数转换。
>
> 同时也有其逆变换
>
> $$
> F(k)=\frac 1 {k!} \sum_{i=0}{k \brack i} S(i)
> $$
>
> 由此可以窥见:方幂转下降幂,下降幂转方幂,斯特林恒等式等。
第一类斯特林数表:
|$n$| $n\brack 0$ | $n\brack 1$ | $n\brack 2$ | $n\brack 3$ | $n\brack 4$ | $n\brack 5$ | $n\brack 6$ | $n\brack 7$ | $n\brack 8$ | $n\brack 9$ |
|:-------:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
| $0$ | $1$ | | | | | | | | | |
| $1$ | $0$ | $1$ | | | | | | | | |
| $2$ | $0$ |$1$| $1$ | | | | | | | |
| $3$ | $0$ |$2$| $3$ | $1$ | | | | | | |
| $4$ | $0$ |$6$| $11$ | $6$ | $1$ | | | | | |
| $5$ | $0$ |$24$| $50$ | $35$ | $10$ | $1$ | | | | |
| $6$ | $0$ |$120$| $274$ | $225$ | $85$ | $15$ | $1$ | | | |
| $7$ | $0$ |$720$| $1764$ | $1624$ | $735$ | $175$ | $21$ | $1$ | | |
| $8$ | $0$ |$5040$| $13068$ | $13132$ | $6769$ | $1960$ | $322$ | $28$ | $1$ | |
| $9$ | $0$ |$40320$| $109584$ | $118124$ | $67284$ | $22449$ | $4536$ | $546$ | $36$ | $1$ |
#### 3. 某一个变量范围比较小,然后又是求类似交/并的,考虑容斥反演。
- [BSOI 13317 【8.13NOIP模拟】最惡の記者 6](http://oi.bashu.cn/p/13317) $k$ 比较小,对 $k$ 进行容斥。
- 某一道 AC 自动机 + 容斥的题目。
#### 4. 遇到一些需要动态开点线段树的题目,考虑是否可以先进行离散化。
- [BSOI 13316 【8.13NOIP模拟】网格染色](http://oi.bashu.cn/p/13316) 先将左右节点离散化再上线段树。
- [BSOI 13321 【8.15NOIP测试】最小化](http://oi.bashu.cn/p/13321) 先将值域离散化后再线段树优化 DP。
#### 5. 曼哈顿转切比雪夫:$(x,y)$ 映射到 $(x+y,x-y)$ 那么则有 $|x_A-x_B|+|y_A-y_B|$ 转为 $\max(|x_A-x_B|,|y_A-y_B|)$。
- [BSOI 3185 「NOI模拟」图论科技](http://oi.bashu.cn/p/3185) 考虑转成切比雪夫距离再上费用流。
- [AT_arc076_b [ABC065D] Built?](https://atcoder.jp/contests/abc065/tasks/arc076_b) 受到启发:如果是最小曼哈顿生成树,考虑转化为切比雪夫,然后再考虑贪心。
#### 6. 树链剖分相关的题目,建议将重心定为根,这样可以减少常数。
- [P4751 【模板】动态 DP(加强版)](https://www.luogu.com.cn/problem/P4751) 可以用重心当根。
- [BSOI 13324 「NOIP模拟」树上的回忆 II](http://oi.bashu.cn/p/13324) 用重心当根,然后再加快读快写就会快不少。
#### 7. 对拍去重
直接将其扔到 `set` 里面再拿出来。
#### 8. 多端点定序枚举问题的优化
即枚举一个序列 $\{p_i\}$ 满足 $1\le p_1\le p_2\le \cdots\le p_{k-1}\le p_k$,这个复杂度是 $O(n^k)$,但是实际上有一个 $\cfrac{1}{k!}$ 的常数,所以时间复杂度应该是 $O(\cfrac{n^k}{k!})$。
#### 9. 差分转换
- [ABC421G - Increase to make it Increasing](https://atcoder.jp/contests/abc421/tasks/abc421_g) 这里区间加,全局单调不降不好描述,把整个数组差分一下,就变成点对前面点加 $1$,后面点减 $1$,使得整个数组大于等于 $0$。转为网络流模型。
- [AGC006C - Rabbit Exercise](https://atcoder.jp/contests/agc006/tasks/agc006_c) 期望分析一下,变为单点进行这样的操作:$f_i=f_{i+1}+f_{i-1}-f_i$。数形结合,相当于沿着 $x=\frac{f_{i+1}+f_{i-1}}{2}$ 翻折。
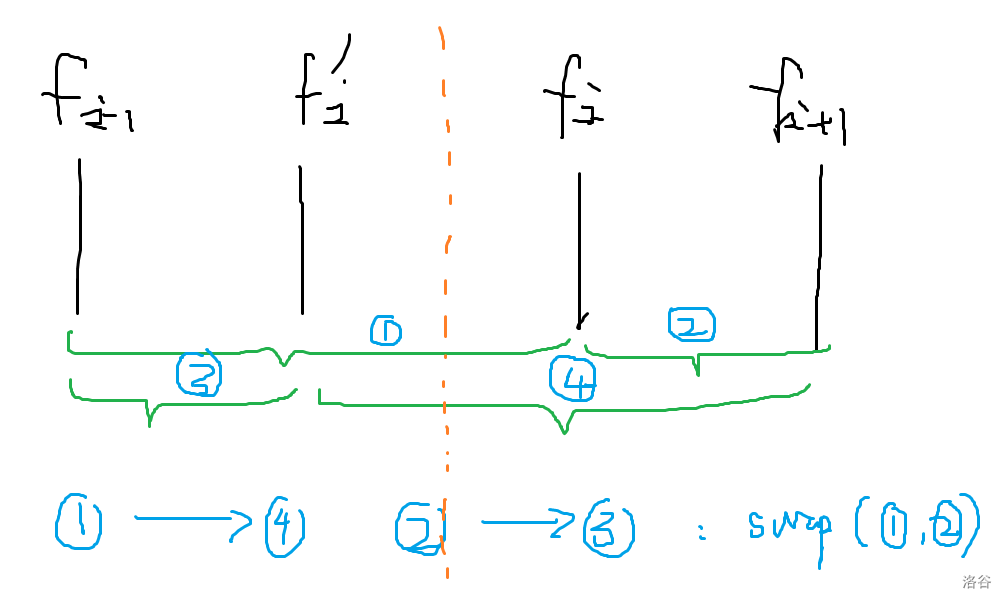
类似这样,相当于反转差分数组,然后我们考虑差分数组,就相当于每次反转相邻的两个位置。根据置换,可以用环大小来表示这个到达的位置。
#### 10. 计数转概率/转期望
- [ARC086C Smuggling Marbles](https://atcoder.jp/contests/arc086/tasks/arc086_c) 列出转移方程,用长链剖分优化。发现要维护一个全局乘的乘法标记,较难维护。**我们考虑将对象从计数转为概率,一开始状态为计数每一层出现石子的情况数量,改为求每一层出现石子的概率**。此时不用因为当前结点选还是不选将整个 DP 数组乘 $2$。 原因是我当前结点选和不选,DP 数组对应的原计数对象的所有情况,都会出现相同次,换言之,我相当于用概率来把这个某个点乘 $2$ 的贡献,转到了最后相乘。
#### 11. 图论问题/排列问题和基环树森林
每个点恰有一条出边,是内向基环树森林;每个点恰有一条入边,是外向基环树森林。
- [AT_agc008_e [AGC008E] Next or Nextnext](https://www.luogu.com.cn/problem/AT_agc008_e) 考虑建基环树森林并分类讨论。
#### 12. 树上选路径问题的思路
##### **[P5021 [NOIP 2018 提高组] 赛道修建](https://www.luogu.com.cn/problem/P5021)**
树上选路径问题,首先考虑二分,然后从下往上贪心选边。
**这里采用这样的贪心思路:对于一个结点,其所有儿子结点传上来的路径只有一条路径可以传到其父亲结点上。所以在儿子结点优先匹配两条断头的路径,一定比传上父结点要优。**
原题中我们需要选出若干条长度 $\ge l$ 的路径,考虑怎么选最好,维护儿子传上来的所有路径长度的 `multiset`。
- 先把所有 $\ge l$ 的路径计入答案并删除。
- 然后从小到大扫,对于一个 $x$,每次找到一个 $y$ 使得 $x$ 和 $y$ 不是同一个元素并且 $x+y\ge l$,则把 $x,y$ 同时删除,计入答案。
- 否则直接删除,作为最大值的一部分,将最大值传上父亲。
- 通过 `multiset` 的 `begin()` 函数 $O(1)$ 找到最小值。
这里有个问题,为什么不能选最大值然后扫最小值?因为如果选最大值,有可能把传上父亲的 `maxn` 劣化了:比如现在 $l=23$,集合元素为 $\{5,18,19\}$,扫 $19$ 会把 $5$ 算到,然后传最大值为 $18$。但如果扫最小值则不会有这样的问题。
那为什么扫最小值是对的?我们的目的是,我们求出子树内最大的匹配次数,然后在此基础上使得传上去的值最大。从小到大扫最小值,可以保证如果当前 $x$ 能匹配到 $y$,那就不存在比 $x$ 小的 $x'$ 使得 $x'+y\ge l$(因为 $x'$ 在此之前已经扫过了,否则其一定可以在先前就将 $y$ 匹配到)。所以选 $x$ 匹配能够传上去的值保证最优。
##### **[AT_arc088_d [ARC088F] Christmas Tree](https://www.luogu.com.cn/problem/AT_arc088_d)**
这里是,**在保证每条路径均 $\le B$ 下,使得路径数量最少,并能覆盖整棵树**。
和上一题比较一下,“**在保证每条路径 $\ge l$ 下,使得路径数量最多。**”
这道题这样描述:把路径数量最少,转化成合并树边使得合并次数最多。
沿用上一题思路:维护 `multiset` 从大往小扫,每次对于最大的 $x$,找到最大的 $y$ 使得 $x+y\le B$,并删除 $x,y$,计入答案。把子树最小值传上去(没有则为 `inf`)。
#### 13. 指数分治
指数分治是一个常见的技巧,多用于一般复杂度无法接受的范围。更广泛地,当一道题目因复杂度瓶颈时,思考能否将某两半东西,取较小地部分枚举,快速算较大部分的值。
#### [AT_abc423_g Small Multiple 2](https://atcoder.jp/contests/abc423/tasks/abc423_g)
枚举前后数字长什么样。朴素枚举是枚举后面的数字,在 $[0,10^d)$ 枚举,其中 $d$ 是满足 $10^d\ge k$ 的最小 $d$。其中等于 $d$ 时一定存在解。
发现这样一个性质,考虑数位对数字的偏序关系,发现当 $x>y$ 时,任意 $x$ 位数一定比任意 $y$ 位数大。既然 $|S|+d$ 一定存在解,那么所以这个数数位不可能超过 $|S|+d$。
引导我们对前后数字进行分治。
枚举后面的数,用 Exgcd 算出前面最小的值。
枚举前面的数,用取模算出后面最小的值。
最后比较可以这样,如果两个答案串中 $S$ 在答案串位置,那么则直接比较数字大小。
最后只会剩下 $O(d)$ 个候选答案串,直接暴力比较即可。
其实这道题还有一个坑。
**数据范围是 $10^9$ 时,不一定与复杂度没有关系,有可能是根号分治/bitset 优化。**
**不要下意识认为其只是为了卡暴力/防止爆 `long long`**。
#### 14. 排列枚举 ($x!!=x(x-2)(x-4)\cdots$)
[AT_arc095_c](https://atcoder.jp/contests/arc095/tasks/arc095_c)。
对称性排列枚举,考虑先枚举排列的匹配,然后再枚举其在排列一边的位置。这样复杂度是 $O(n!!)$ 的。关于如何枚举:首先在 DFS 时,假设 $x,y$ 匹配,在枚举到 $x$ 时往后枚举,并钦定 $y$ 与 $x$ 是一对匹配元素。
本质上,排列对称性与不同相对位置无关,例子就是 $1,3,2,4$ 和 $1,2,3,4$ 、$3,1,4,2$ 是一致的。
#### 15. 三维偏序转二位偏序
[BSOI B3444. 【10.13NOIP模拟】接雨滴](http://oi.bashu.cn/p/B3444)
考虑三维偏序转二维偏序:考虑能否去掉一维条件,使得另外两维自动推导到这一维条件;或者如果遇到对称分类讨论,比如绝对值等,可以考虑能否直接用两部分讨论式子直接拼凑出来,省去分类讨论。
比如:
$$
\begin{aligned}
t_j\ge t_i \space\space\space (t_j-t_i)v_c\ge |p_j-p_i|
\end{aligned}
$$
满足这两个条件偏序。
朴素做法,考虑拆绝对值:
$$
\begin{aligned}
t_j\ge t_i \space\space\space (t_j-t_i)v_c\ge \max(p_j-p_i,p_i-p_j)
\end{aligned}
$$
转为三维偏序:
$$
\begin{aligned}
t_j\ge t_i \space\space\space p_j\ge p_i \space\space\space(t_j-t_i)v_c\ge p_j-p_i\\
t_j\ge t_i \space\space\space p_j< p_i \space\space\space(t_j-t_i)v_c\ge p_i-p_j\\
\end{aligned}
$$
发现没有必要这样,考虑 $(t_j-t_i)v_c\ge |p_j-p_i|$ 成立,又因为 $v_c\ge 0$ 则 $t_j\ge t_i$ 一定成立。或者两个三维偏序中后两个条件都可以推导出前一个条件成立。
#### 16. 加和字符串偏序
考虑对字符串新定义一种偏序,具体地对于 $S$ 和 $T$:
$$
S+T < T+S \Rightarrow S <' T\\
S+T \le T+S \Rightarrow S \le' T
$$
有如下性质:
1. 其具有传递性,即对于 $A<'B$ 且 $B<'C$ 则 $A<'C$。所以可以排序。
- 证明考虑:$S<'T$ 等价于 $S^{\infty}<T^{\infty}$,后者具有偏序关系,则前者具有。($S^{\infty}$ 指 $S$ 不断重复的串。)
- 考虑直接证明可以把小的串不断拼在后面,讨论其前缀相同时后面的相等性。
- 感性理解可以考虑这样,把两个串当作一个向量,拼在一起则是向量相加:
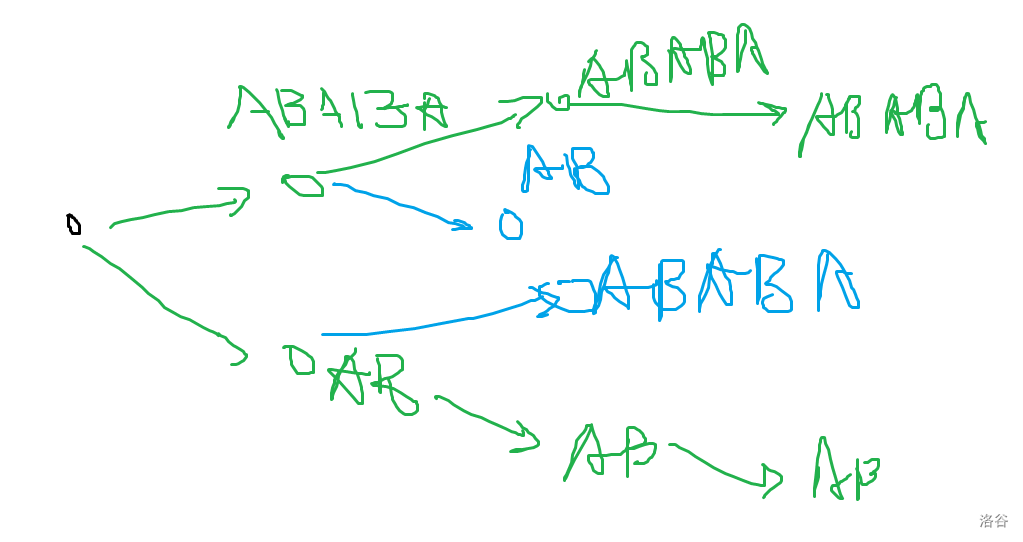
- 比如 `ABABA` 和 `AB` 比较,考虑后面的向量的角度要比相同向量在前面的位置的角度要小,所以可以理解为后面向量对加和的向量的影响更小。**考虑不断往两边走,等价于走一次之后往中间走,然后比较哪一个对向量的影响更大。** 可以假想中间有一条线割开两边。
- 以后遇到一些向量的无限项加和的比较,并且后面的向量的影响越来越小,考虑能否把其交换一下,考虑前一个向量先导得更多。
- 就是
$$\vec A+\vec A+\cdots <=> \vec B+\vec B+\cdots$$
- 考虑
$$\vec A + \vec B <=> \vec B + \vec A $$
- 这个可以考虑优化复杂度。
- 也可以:
$$\vec A + \vec B <=> \vec B + \vec A $$
- 考虑
$$\vec A+\vec A+\cdots <=> \vec B+\vec B+\cdots$$
- 这个可以使比较式两边用同一种变量表示,考虑可以优化偏序关系、定序。
2. 对于 $n$ 个字符串按某种顺序拼接使得合成串字典序最小,等价于对这 $n$ 串按 $<$ 偏序排序。
- 证明考虑调整法。考虑两个 $>'$ 转为 $\le'$ 一定不劣。冒泡排序最后可以转为上升段。
- 实际例题:[AT_abc225_f](https://atcoder.jp/contests/abc225/tasks/abc225_f)。
#### 17. 线性基异或和为 $x$ 的方案数
[BSOI B3510. 【10.14NOIP模拟】AND 和 XOR](http://oi.bashu.cn/p/B3510)
根据打表发现,对于一个大小为 $S$ 的线性基有 $n$ 个自由元,则对于线性基能异或出来的 $2^S$ 个数的每个数,都恰好有 $2^n$ 种表示方法。所以一个线性基表述要么为 $2$ 的自由元个数次幂,要么为 $0$。
#### 18. 一个 01 序列相邻删除相同/不同元素
[P14015 [ICPC 2024 Nanjing R] 生日礼物](https://www.luogu.com.cn/problem/P14015)
考虑可以将偶数位翻转,那么现在就变为了删不同/相同元素,**原理是每删除两个数,剩下所有元素的奇偶性不发生改变。** 可以对正解有一定提示作用。
需要做:[CF1615F LEGOndary Grandmaster](https://www.luogu.com.cn/problem/CF1615F)。
#### 19. 若干个单调性询问考虑转二分为扫描线
[BSOI B3525 【10.18NOIP模拟】单调不降序列](http://oi.bashu.cn/p/B3525)
如果若干个询问呈单调性,考虑不去二分,转为指针去扫一遍。
#### 20. 树上问题一个点是否为另一个点的祖先
[BSOI B3525 【10.18NOIP模拟】单调不降序列](http://oi.bashu.cn/p/B3525)
不要什么都想树剖,考虑 DFS 序是否包含/被包含。
所以这个题,考虑先二分答案,然后转为贪心选择大于等于前一项的最小值,**在增加下标的同时维护一个 $J$ 表示当前点是否可以选这个值,双指针增加 $J$ 并检查这个点是否可以在 $lth$ 步到达**。然后发现其实是基环树是否包含,如果是在同一个基环树内,先判断环上距离,**然后再考虑 `dfn-bot` 是否包含,来 check 祖先关系。** 用深度数组算出这个值即可。
#### 21. 二项式定理:$(a+b)^n=\sum_{i=0}^{n}\binom{n}{i}a^ib^{n-i}$。
[B3527 【10.18NOIP模拟】米奇与数字](http://oi.bashu.cn/p/B3527)/[P8362 [SNOI2022] 数位](https://www.luogu.com.cn/problem/P8362)。
如题。
#### 22. Kruskal 重构树
[P11985 [JOIST 2025] 比太郎之旅 2 / Bitaro's Travel 2](https://www.luogu.com.cn/problem/P11985)
1. 两个点的最大边权最小路径中其中一个最大的点在两点 K 树的 LCA 上。
2. 对于边权建 K 树考虑直接把边当作点,把边当作点,把边权当作点权。把点权用极大/极小值忽略掉即可。
3. 一个图上,每个点有点权 $a_i$。考虑求一个点游走,到达的点点权不能超过 $a_i+L$ 的点中的最大点权。**这恰好等于点权 K 树中 $i$ 往上跳父亲跳到深度最小的使得 $a_j\le a_i+L$ 的最大 $a_j$。**
- 考虑这样证明:
- 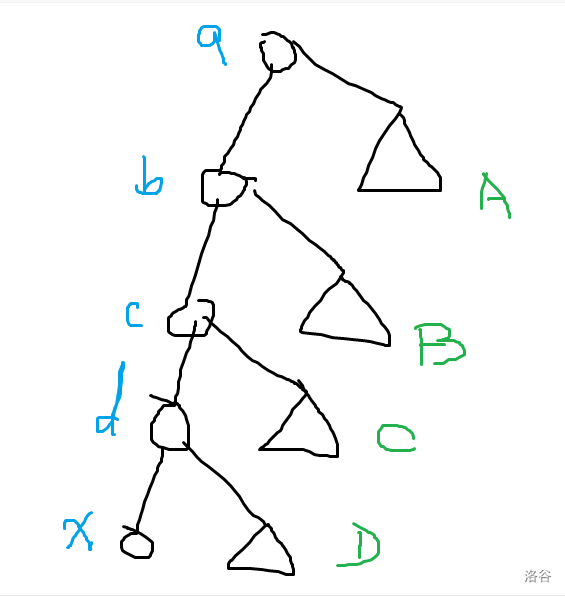
- 考虑 K 树性质,对于某个点对其权值为 LCA 的权值。那么对于一个点 $x$ 不断往子树上爬父亲时,其兄弟子树的所有点到 $x$ 的距离 **恰好** 等于当前父亲的权值。比如说从 $x$ 爬到 $d$,那么从 $x$ 到 $d$ 的其它子树的所有点的权值都等于 $d$ 的权值。
- 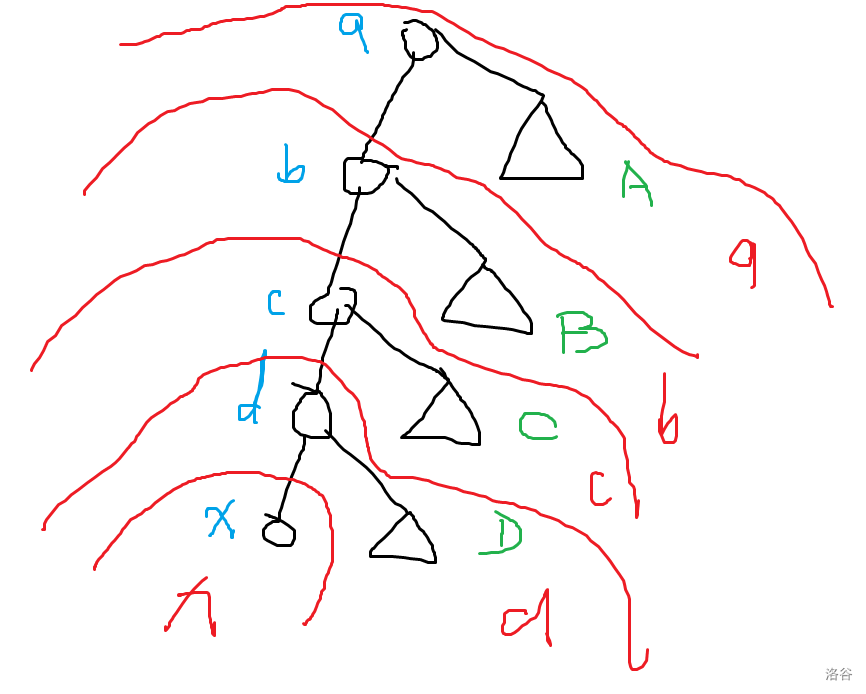
- 最终从 $x$ 出发,到达其他点的路径最小权值恰好如 **辐射状** 往外散开,且每一部分以 $x$ 的父亲作为割分,越往外权值越不优。(注意点权相同时,割分段不能直接用 LCA 来表示,而是一段连续段来表示。)
#### 23. 点覆盖区间模型
最朴素的问题是:给出 $n$ 个区间,然后选出若干个点,使得覆盖所有区间,且选出的点数量最少。
一个常见的贪心思路是:“右排左扫”,就是将其按右端点排序,然后从左边开始依次扫描到右边,每一次贪心选择该区间选不选,若需要选择,则选择这个区间的最右端。
考虑为什么要这样子做:发现对于一个区间,每次把要选区间的右端点 $r$ 选择,等价于说:右端点小于 $r$ 的已经用最优策略解决了,此时 $r$ 又必须要选择,所以选择 $r$ 是最优的。
这种贪心实际上在说这个:我用恰好 $i$ 个点最多能覆盖多大的区间,希望最小化 $r$ 使得右端点小于等于 $r$ 的都被覆盖了。
某个点覆盖后,未覆盖的区间一定被分成了两部分。这就启发我们这个可以做区间 DP。
- [BSOI B3544 【10.25NOIP模拟】修复故障](http://oi.bashu.cn/p/B3544)
> 考虑设 $f_{l,r}$ 表示将左右端点都在区间 $[l,r]$ 的区间的答案。枚举区间的某个端点并强制选择其,分治到两边。
所以:点覆盖区间模型 的 一个偏序关系 是:对于 [l,r] 包含的区间构成一个偏序集。
也可以这么来理解,我当前选了之后,后面的区间会被割开变为两半,且分界点无交。这个同时可以在 DP 时用作,状态为在这里选择时的贡献。可以从上一次分割点转移,保证没有区间完全在两个分割点之间即可。
- [BSOI B3529 【10.20NOIP模拟】超速检测](http://oi.bashu.cn/p/B3529) / [P12761 [POI 2018 R2] 列车员 Conductor](https://www.luogu.com.cn/problem/P12761)。
#### 24. Ad-hoc 计数题中的 DP 状态优化
##### 若干的子序列计数方法
- [B3570 【11.03NOIP2025模拟】构了个造](http://oi.bashu.cn/p/B3570)
#### 25. 随机化技巧和骗分
- [B3570 【11.03NOIP2025模拟】构了个造](http://oi.bashu.cn/p/B3570)
这道题为什么场上没有做出来。发现第一个原因是 checker 写得不够简洁。
常见的子序列 DP 可以这样设置状态:以当前位置结尾的,计数以第一次出现时当前位置为结尾的子序列数量。DP 就是从 $|\Sigma|$ 个字符转移。
转移类似于 $f_0=0$,$f_i=\sum{f_{last_{c_i}}}+1$。
答案为 $f_{n+1}$。
也有将这个过程取反,那么就变为 $f_0=1$,$f_i=\sum{f_{last_{c_i}}}$,答案为 $\sum_{i=1}^n{f_i}$。
然后就会有线性的两种转移方法:
[here](https://www.cnblogs.com/hzy1/p/16878663.html)。
一种是前缀优化,设 $f_i$ 表示以 $i$ 结尾且之前没出现过的子序列个数,那么 $f_i=\sum_{j=last_{arr_i}}^{i-1} f_j$。
另一种是容斥,设 $g_i$ 表示前缀的答案,发现当前的贡献为 $2g_{i-1}$,但是会算重已经算过的部分为 $g_{last_{arr_i}}$,减去。然后加上自己这一位置的贡献。
但是发现这个也不行。
这样才行。就是算 $f_{i,0/1}$ 表示在 $1$ 到 $i$ 的子序列以 $0/1$ 结尾的数量。然后发现当前这个结点首先只会对 $f_{i,arr_i}$ 有影响。考虑转移,要么前面为 $0$ 为 $f_{i-1,0}$,要么为 $1$ 为 $f_{i-1,1}$,要么单独开一个为 $1$。所以:$f_{i,arr_i}=f_{i-1,0}+f_{i-1,1}+1$,$f_{i,1-arr_i}=f_{i,1-arr_i}
考虑刻画为向量则为:现在有两个数 A,B:一开始全为 0,然后每一次要么 A\leftarrow A+B+1,要么 B\leftarrow A+B+1。一种方法是整体替换,把 A 写成 A+1 然后就变为 (A+1)\leftarrow (A+1)+(B+1),发现是更相减损法。
题解的做法是直接随机最后的 A 和 B,然后就判断是否互质和是否 60 步以内有解。Felix72 提供了一种做法,是在 \frac 1 x=\frac x {1-x} 的位置,即黄金分割点附近找。速度会快一些。
所以做不出来的时候可以适当考虑一下随机化做法,比如之前的 CF2151G2/CF2150E2,已经在 G1 有分治做法,考虑直接将第一次得到的做法,直接作用于第二题的一开始,然后将剩下的随机化。
考虑如果没有发现可以整体替换(把 A 写成 A+1 然后就变为 (A+1)\leftarrow (A+1)+(B+1))的时候能否做?讨论一下,其实可以直接减去即可。
26. 数据结构维护,考虑独立的操作能否分别维护
-P9776 [HUSTFC 2023] 狭义线段树
考虑操作 1 和 2 可以分开。如果某个思路断了的时候,考虑能否用两个数据结构分开维护。
27. 把 n 个物品分成若干份,每份为 d 或 d+1,那么合法 d 数量为 O(\sqrt n) 级别
(from AI)
给定 n 个小球,若存在一种方式将小球分成若干份,每份大小为 d 或 d+1,则称 d 是合法的。需要证明合法 d 的数量为 O(\sqrt{n})。
证明
合法 d 的条件等价于:存在正整数 k(总份数),使得:
k d \leq n \leq k(d+1)
或等价地:
d \leq \frac{n}{k} \leq d+1
其中 k \geq 1,d \geq 1 为整数。该条件意味着存在整数 k 使得区间 \left[\frac{n}{d+1}, \frac{n}{d}\right] 包含至少一个整数(即 k)。
由整除分块的知识,\lfloor\frac n k\rfloor 的数量为 O(\sqrt n)。所以合法 d 的取值数量也为 O(\sqrt n) 个。
28. 把一个有向图添加一个虚点和一些边,使其变为欧拉回路图,添加最少边数的方案是,把每个点入度和出度补成相等(不考虑连通性)
P8291 [省选联考 2022] 学术社区
这个的 AC 性质的部分,需要解决一下问题:
(一开始我想的时候,是想得有所偏差,即认为只有每个学术消息可以引出一条路径,但是题目其实每条边都会在最后的总体输出上出现,所以一条没被学术消息引出的路径,它只是在一开始没有得到这个权值,但是在路径的中间还是可以得到权值。)
路径覆盖可以想一下欧拉回路。(补一下思维链的内容)
你发现一个点有入度有出度,同时删除 1 入度和 1 出度使两条链连起来一定不劣。
最后每个点只剩下若干入度,或者只剩下若干出度。若干出度可以用学术消息抵消一部分,剩下的发现这里没有可以优化的地方。若干入度代表链到达这里已经终止。看势能,全图的若干入度和恰好等于若干出度和,而每个出度恰好对应一条链的开头。
注意,学术信息的冗余的多少对答案没有影响。
所以此时再贪心选择学术信息,没有的则说明这个链开头不是学术信息。
发现这个不是很能算方案。考虑如何往欧拉路径上靠。
发现出度大于入度的点,其多余的出度恰好作为一条链的开头;对于入度大于出度的点,其多余的入度恰好作为一条链的结尾。
我们只需要在入度出度不等的地方补上其入度/出度,就可以使所有路径头尾都在虚点处相连。那么就可以得到一个欧拉路径图。
29. 快速变换:对于不能直接操作点积的变换快速幂,可以考虑采用朴素分治快速幂。
- 任意模数多项式快速幂(指数在模意义环上进行,即序列长度为 n,则有 x^a \cdot x^b = x^{(a+b) \bmod n}))
30. 当打表发现有一些数列类似于组合数的行,但是不像,且中间有若干个数相同,且是 2 的幂次,要注意其是否是组合数平移若干个相加的结果。
比如:
1,3,4,4,4,4,4,4,3,1\\
1,4,7,8,8,8,7,4,1\\
1,5,11,15,15,11,5,1\\
看到这个数列感觉很像组合数,两边对称,且有组合数的影子。考虑是否为多个组合数平移得到的结果。
1,4,7,8&,8,7,4,1\\
1,3,3,1&\\
1,3,3&,1\\
1,3&,3,1\\
1&,3,3,1\\
&\,\,\, 1,3,3,1
\end{aligned}
其它的也同理。
来源启发:CF1784F Minimums or Medians 的暴力打表。
31. 条件概率
P13350 「ZYZ 2025」遗传 / B5531. 【1.19省选模拟】观测
原题面比搬题人给的题面还要抽象。
就是说如何描述这样的条件概率题目?
把全局找出来,也就是对于枚举所有 S=(a_i,b_i)^n 元组,对其概率乘上其在“观测结果下”的合法性(合法为 1,不合法为 0)求和。即为在“观测结果下”合法相对于不考虑“观测结果”的比值。即 {P(S')}。S' 表示所有合法集合。
然后找到二元组钦定的概率,即 S'=(a_i,b_i)^n 再钦定某个 (a_{cu},b_{cu})=(x,y) 的。我们这种集合为 S''。要算即为 \cfrac {P(S'')}{P(S')}。
直接用条件概率理解就是:已知 S' 发生算 S'' 发生的概率,等于 S' 和 S'' 同时发生的概率除以 S' 发生的概率。
由于这里 S''\subseteq S' 所以就是 P(S'') 除以 P(S')。
但是如果不是包含,算 P(B|A)(事件 B 基于 A 发生的前提下发生的概率)。那么可以理解为,我画一个维恩图,然后将 A 的圆圈拿出来看一下 B 交 A 的比例有多大,那么就有 B 发生的概率。即是 A 作为全体样本空间下 B 样本的比例。
互相独立的两个集合,其在韦恩图上形如
其中有 B 基于 A 发生而发生的概率(P(B|A))等于 \cfrac {P(B\cap A)}{P(A)},由于其独立,那么 P(B|A)=P(B)。所以 A\cap B 在 A 的占比等于 B 在全体样本空间的占比。可以理解为 A 对整个样本空间进行了一个线性等比例变换。
互相排斥的两个集合形如:
即在 A 作为全体样本空间下,B 发生的概率为 0。在 B 视角下同理。
32. 系数倒推的技巧
P13350 「ZYZ 2025」遗传 / B5531. 【1.19省选模拟】观测
接 31。
列出 DP 方程,发现求解的时候我们每次只会改变某个点的 DP 数组,使得其中某个值保留,其它值变为 0。求解其对最后根节点的值的影响。
可以考虑变为 0 的三个数对最后数组的影响。
可以理解为:如果其它都不发生改变,那么只考虑这个点向上的这一条链,那么其它的点都给到了一个系数,最后这三个点变为 0 的影响,是其向上的所有系数之和乘上其权值改变的大小。
所以倒着求一遍系数即可。
CF1810G The Maximum Prefix
正着做后效性太强,倒着做可以,但是发现每次概率要重新推,但是你发现其是平移概率,所以考虑把 DP 倒过来,那么每次相当于在后面新添加一个概率。
还有一种记录“与目标距离”,即不钦定一个最大值位置,转而钦定当前位置和最大值的距离,以及是否到达最大值来转移。那么怎么记录贡献呢?我们可以把贡献扔到 DP 中,直接将初态设为权值,那么我们就不是在算方案而是再算贡献。
参考文章。
所以:
- 如果 DP 平移转移,或者使得初态端点相对于终态发生相对移动时,考虑从终态出发倒推初态。
- 可以不算方案,直接计算贡献,钦定某个贡献在达到某个要求即可得到,那么把其算在一开始的 DP 中,就不用记贡献的后效性了。
33. 区间连通块/区间生成树问题,考虑扫描线并用 \min(u,v) 为权值,用 LCT 维护最大生成树
这两道都是要维护区间的连通性,第一道维护区间的点是否通过这些边连通,第二道维护的是区间连通块个数。这些可以转为区间生成树森林的树的个数,再转为区间生成树森林的点数减去边数。
那么我们维护点数和边数即可。
边数怎么维护?对于每个区间,我们肯定是希望先选这个区间内的边,那么选出来的就是一个生成树森林。然后我们发现对于 r 相同的一组区间,当 l 不断减小时,其区间包含的边形成集合的偏序关系。由于 MST 具有边集合的偏序关系,那么我们希望用 MST 来刻画这个问题。
对于每条边 (u,v) (u<v),其的生效的 r 处于 [v,n],其的加边优先级为 u(优先级大为优先) ,那么我们将其的权值标为 u,在 v 时刻加入,此时的 MST 即可以完全表示一个后缀区间的连通性。
注意到,这样维护,区间的信息我们是完全掌握的,包括和,最值等。
34. 模意义下高斯消元和行列式计算
有可能没有给到模数为质数的情况,不一定要求逆元,考虑可以从辗转相除法入手,不断两个相消,最后可以得到合理的线性方程组。
35. 二分图的最大匹配等于最小顶点覆盖,最大独立集等于总点数减去匹配
最大匹配可以 Dinic。
如何构造覆盖和独立集?
覆盖
考虑最后的匹配形成的交错树,会发现我们希望每一个匹配两边恰好选择一个点使得其完全覆盖。那么就思考每条边选哪种。
考虑上面四种情况,其中第四种不存在(可以更优)。
第一种要求选右部点,第二种要求选左部点,第三种可以任选一边(或上面一部分选右边,下面一部分选左边)。如何区分这种情况。
这样做,先钦定选右边的,再把要求选左部点的第二种情况特判掉。
特判的方法是走交错树,把其上面的左部点标记为强制选,把其上面的右部点标记为强制不选。恰好发现右边没有标记的点都是匹配点。
怎么保证覆盖完所有的点?考虑每个点至少属于一个交错树,因为不会有第四种情况,那么第二种情况这样走不会和第一种情况撞上,所以其钦定的点,不会和第一种情况的冲突。
所以右部走交错树(匹配边走完的所有非匹配边都要走),然后左部的标记点,右部的非标记点即为所求。
怎么证明最优?因为少于匹配数一定这些边存在一条没有覆盖。
独立集
可以直接用覆盖点的补集即可。
因为如果有两个点是一条边两个端点,那么这条边可作为新的匹配。之所以不能更优,是因为更优则一定存在一条边两边都选。
所以思考路径是:
二分图独立集 \rightarrow 二分图点覆盖补集 \rightarrow 交错树上标记,一边选标记,一边不选标记 \rightarrow 最大匹配
同时有这个问题也是转到独立集上:
有 n 个集合,每个集合分别包含 1 到 m 的某些整数,选择 k 个集合,令这 k 个集合交大小为 d,最大化 k+d。(其中 k 无限制,特殊地如果 k=0 则 d=m。)
这个问题就这样想,假设有一个方案合法,那么其二分图上的这 k 个点和 k 个集合的交都存在两两的跨越边,就变为二分图上的最大团(假装左部点和右部点内部都有连边),转补图即为求最大独立集。