哈希学习笔记
三点水一个各
·
·
个人记录
经过某膜你赛不堪入目的暴击(AK->200)后,菜鸡开始学习哈希了:
什么是哈希?
对于线性表(1,43,46,75,90,324,1353)
如果用一维数组直接存储,只需要A[1..7],虽然空间是O(7)但是查找某元素需要时间是O(log n),时间上欠佳。
如果定义A[key]=key,那么需要A[1..1353],虽然时间是O(1),但空间是O(1353),也就是O(\max a[i]),空间上欠佳
能不能有一种数据结构使时间空间都相对优呢?
她就是哈希表。
设计一个函数h(key)=key \bmod 13
然后把key存储在A[h(key)]中,即A[h(key)]=key
使数据都能存储在A[0..12]中。
此时建表和查找所需时间均为O(1),空间也为O(mod) (mod为模数)。
一般实现
设计一个函数h(key)(不一定是\bmod)
然后把key存储在A[h(key)]中,即A[h(key)]=key
若有冲突(A[h(key)]已有另一数值),用另一函数I进行映射,计算出I(h(key)),若还是冲突,则继续I(I(h(key)),直到不冲突为止。
例如I可以是I=h(key)+1。
要巧妙选择h与I函数。
选择h有以下六种常见方法:
1.直接定址法
#### 2.除余法
$h(key)=key\mod C$($C$为一个常数)
#### 3.数字分析法
去除一些辨识度低的数字(重复出现频率过高)
| key | h(key) |
| :----------: | :----------: |
| $000309526 $ | $326$ |
| $000217442 $ | $242$ |
| $000417414 $ | $414$ |
| $000319628$ | $328$ |
| $000509457$ | $557$ |
| $000619471$ | $671$ |
第$1,2,3$列全是$0$完全没有辨识度,第$5,6,7$列都由两个数组成,故删去。
#### 4.平方取中法
先将数平方,取中间几位。
| $key$ | $key^2$ | $h(key)$ |
| :---------------: | :---------------: | :---------------: |
| $0100-$ | $0010000$ | $100$ |
| $0110-$ | $0012100$ | $121$ |
| $1010-$ | $1020100$ | $201$ |
| $1001-$ | $1002001$ | $020$ |
| $0111-$ | $0012321$ | $123$ |
(我谢罪表格制作有些恶心)
平方后,取$3,4,5$位数字。
#### 5.折叠法
把数字分成若干段,逐位相加
如分解$1919810$:
```cpp
1 9 1
9 8
1 0
_______
2 9 9
```
#### 6.基数转换法
转换进制,然后分析数字,取若干位数。
***
处理冲突有以下两种常见方法
#### 1.拉链法
冲突后,拉出一条链子(链表)存储冲突的元素。
就像这样:
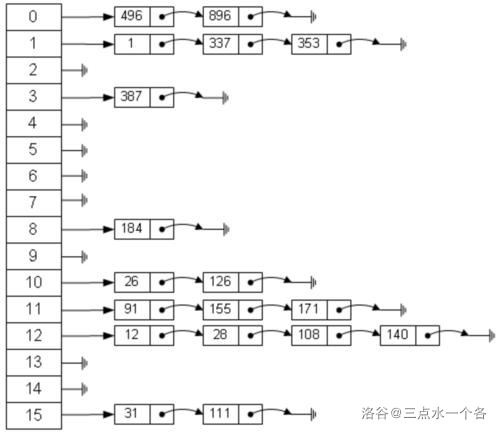
拉链法的另一种办法就是从后往前找空的地方,找到了就插进去,并用链表把他接进去。
#### 2.开地址法
冲突后,按照探查序列查找空的地方,找到了就插进去。
与拉链法不同的是,开地址法按照一定的顺序,也就是前面提到的$I$函数映射,一般为:
$$I(i)=(h(key)+i)\%m(1\le i\le m)$$
开地址法不能处理数据的删除,因此要删除数据时,只能用拉链法。
还有一种探查法叫做双哈希探查法,就是冲突时用另一个哈希函数,且 $h2(key)$ 与 $m$ 互质,可以简单的定义为
(菜鸡看不懂1.2在讲什么,大概就是再讲哈希的意义,没啥用这里就不记了)
###
参考资料:林厚从《青少年信息学奥林匹克竞赛实战辅导丛书高级数据结构》