【LGR-(-11)】CSP 2020 第一轮(初赛)模拟 题解
bifanwen
·
·
个人记录
博客园同步
CSDN同步
前言
一开始查排名的时候不知道为啥翻遍了排名榜都没找到。
后来才找到了?94 分竟然没找到,佩服佩服。
链接在这 \rightarrow 2020 洛谷初赛模拟
如果乐意直接看答案的话,公布一手:
ABCBA CABCB DBACD
FTTTBA
FFTTAA
FFFTCC
CDDAC
CBDCB
题解
单项选择题
第 1 题,首先符号位是 1(负数),其次 124_{(10)} = 01110010_{(2)},补码即为 10001101,然后接上符号位是 10001110. 选 A.
第 2 题排除法,ACD 都是著名 \text{OJ},选 B.
第 3 题,考虑一个类似 \text{Cantor} 的做法。
所以编号为 $2022$,选 $C$.
第 $4$ 题,~~我竟然错了~~ $\frac{4096 * 2160 * 24 bit}{1024 * 1024 * 8} = 25MB$(物理上的等号,约等于)。选 $B$.
第 $5$ 题,本人也没搞懂是什么算法(后来知道是一个叫 `nth_element` 的东西)可以做到 $\mathcal{O}(n)$,但是好像没说能用算法解决,所以问题转化为四个复杂度最优的是哪个?选 $A$.
第 $6$ 题,$(1)$ 必然是错的,因为没有强调 **连通图**。$(2)(3)$ 都是对的,$(4)$ 也是错的。因为树是无向无环的。选 $C$.
第 $7$ 题,~~我也错了~~ 其实这题类似于合并果子的最小代价,不过是反向的合并果子(拆分果子?),最优方案是:$42 = 15 + 27 = (10 + 5) + (13 + 14)$,代价为 $42 + 15 + 27 = 84$,选 $A$.
第 $8$ 题,根据先中遍历可以唯一确定树。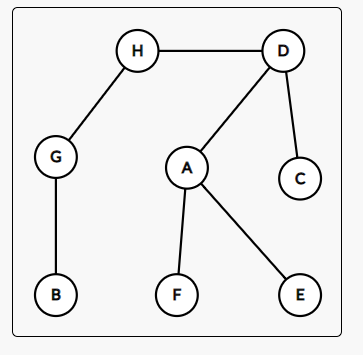
$H$ 是根。然后按照题目的方法(即完全二叉树的存储方法,学过线段树的应该都知道),最大的 $E$ 为 $13$. 选 $B$.
第 $9$ 题,暴力题,不说了,选 $C$.
第 $10$ 题,最优的情况是,第一次查找的就是链表第一个元素,第 $i (i > 1)$ 次查找的是第 $i-1$ 次查找后插入的元素。$\mathcal{O}(k)$,选 $B$.
第 $11$ 题,可以枚举。
|$A$|$B$|$C$|
|---|---|---
|$5$|$1$|$0$|
|$5$|$0$|$1$|
|$4$|$2$|$0$|
|$4$|$1$|$1$|
|$4$|$0$|$2$|
|$3$|$3$|$0$|
|$3$|$2$|$1$|
|$3$|$1$|$2$|
|$3$|$0$|$3$|
|$2$|$4$|$0$|
|$2$|$3$|$1$|
|$2$|$2$|$2$|
|$2$|$1$|$3$|
|$1$|$4$|$1$|
|$1$|$3$|$2$|
|$1$|$2$|$3$|
|$0$|$4$|$2$|
|$0$|$3$|$3$|
$18$ 种,选 $D$.
第 $12$ 题,只有插入排序复杂度为 $\mathcal{O}(n^2)$. 选 $B$.
第 $13$ 题,大概像我这种出题比较多的造数据都会用到。
$[a,b-1] \rightarrow [0,b-a-1] + a \rightarrow \text{rand()}\%\text{(b-a)} + a$,选 $A$.
第 $14$ 题,完全图有 $7 \times 6 \div 2 = 21$ 条边,森林有 $7-1=6$ 条边,删去 $15$ 条,选 $C$.
第 $15$ 题,常识题,选 $D$.
### 阅读程序题
#### 第 $1$ 篇
该程序的功能就是记忆化计算了 $gu$ 函数的值。$gu$ 没有应用意义。可以发现 $gu_{i,j} = gu_{i,j-1} (j \% 2 =0)
- 显然 m 是奇数不影响做法。F.
- 会改变,因为那样会把 =m 的答案也加上了。T
- 删去记忆化的代码会增高时间复杂度,但不影响答案。T.
- 显然,T.
- 建立二维表即可,B.
- 记忆化计算 nm 个值,每次计算复杂度为 \mathcal{O}(m),所以为 \mathcal{O}(m^2n),选 a。
第 2 篇
我也不知道这程序是干嘛的,题错了 1 个。???
不过 f 存的是最短路,老 \text{Floyd} 家都知道。
- 老 \text{Floyd} 家了,肯定影响答案。F.
- 该程序复杂度为 \mathcal{O}(n^4 + m),虽然 m 影响很小,但还是含有的。F.
-
- 显然不变,对 x 和 y 类似的松弛操作没有顺序。T.
- 我是人工算的,A.
- 都说了是 \text{Floyd} 了,A.
第 3 篇
写过 \text{NOIP2016 tg} 组合数问题的人应该都知道,A_{i,j} = C_i^j,\text{sum} 就是杨辉三角的前缀和。
- 显然,i=j 时为 1,F.
- 不是排列数,是组合数。可枚举验证。F.
- 本来应该是对的,但是由于有模数,1000 之内的组合数远远大于 19260817,可能出现加和模之后变小。F.
- 没有溢出问题的话,这样写是对的。这个写法也常用来对负数取模。T.
-
- 手算一下前缀和即可。答案为 50,选 C.
完善程序题
第 1 篇
理解程序的原理很重要,本人在第 2 小题也卡了一会儿。
该原理就是,可以建立树,a_i 为 i 的父亲。从不被关注的叶子节点开始,叶子节点首先枪毙。然后往上走,如果 当前节点不被枪毙 并且 没有人关注当前节点的父亲节点,则毙掉父亲节点。边也要断掉。
- 断边操作需要减掉一个度。选 C.
- 只有不被关注的节点(叶子节点)才会被 \text{dfs},选 D.
- 很显然,对于一条链,分奇偶枪毙。选 D.
- 毙掉叶子节点,选 A.
- 最后出现的是没有访问过的节点,选 C.
第 2 篇
显然,这道题是反向扫一遍,程序原理很简单。反向更新最小值和和,然后直接算、打擂就行。用栈记录最后的答案。
- 初始的和为 s_n,选 C.
- 统计和,选 B.
- 计算除最小值以外的平均值。[i,n] 共 n-i+1 个数,去掉最小值是 n-i 个,特此说明。选 D.
-
- 同样的答案直接加入栈中,熟悉栈的操作。选 B.