浅谈勾股数
COsm0s
·
·
个人记录
今天做暑假作业的时候碰到两组勾股数:\{9,40,41\}\{5, 12, 13\}。
猛然想起似乎很多勾股数都包含相邻两个自然数。
所以在此随笔。
注:本文所包含的勾股数一般指三个数都 \in \mathbb{Q} 且大于 0。
\mathcal{Part\ 1}
此节讨论关于勾股数中包含两个相邻自然数。
对于两个相邻自然数 x,x+1,设剩下一条边为 y,分类讨论。
大的边做斜边。则 x^2+y^2=(x+1)^2。
\begin{aligned}
x^2+y^2&=(x+1)^2\\
x^2+y^2&=x^2+2x+1\\
y^2&=2x+1
\end{aligned}
由此可见,当这相邻两个数之和为完全平方数时,问题可解。
两边分别做直角边。
\begin{aligned}
x^2+(x+1)^2&=y^2\\
2x^2+2x+1&=y^2
\end{aligned}
也就是当函数 f(x)=2x^2+2x+1 取到平方数时,原式有解。
由于作者太菜,无法证明此类勾股数的充要条件。
但是已知在 10^9 范围内,满足此条件的勾股数只有以下几对。
3 4 5
20 21 29
119 120 169
696 697 985
4059 4060 5741
23660 23661 33461
137903 137904 195025
803760 803761 1136689
4684659 4684660 6625109
27304196 27304197 38613965
下面给出 QB 老师的正解。
设 a_n 为第 n 项满足此式的 x。
则有 a_n=7\times a_{n-1}-7\times a_{n-2}+a_{n-3}。
前三项为 0,3,20。
同时我们也可以采用一般公式,即:
## $\mathcal{Part\ 2}
这一节讨论关于勾股数中出现奇数的情况。
首先观察 part\ 1 中第一种情况。
由于相邻两项自然数之和一定为奇数,所以此时的 y 也一定为奇数。
所以我们可以知道,当直角三角形的较短直角边为奇数时可以出现三数都 \in \mathbb{Z}。
下面证明此结论的一般性。
设此奇数边 a 为 2n+1。
\begin{aligned}
a&=2n+1\\
a^2&=(2n+1)^2\\
b&=\lfloor\frac{(2n+1)^2}{2}\rfloor=2n^2+2n\\
c&=b+1=2n^2+2n+1\\
c^2&=a^2+b^2=(2n+1)^2+(2n^2+2n)^2\\
c^2&=(2n^2+2n)^2+2(2n^2+2n)+1\\
c^2&=[(2n^2+2n)+1]^2
\end{aligned}
显然,当 n\in \mathbb{Q} 时,a 都可以取到奇数值,即除一以外所有奇数都有对应勾股数。
下面证明 1 为什么不可取。
显然, 1 只能为短直角边。
设另两边 x,y 使 \{x,y\in\mathbb{Q}|x,y > 1\}。
\begin{aligned}
x^2+1^2&=y^2\\
y^2-x^2&=1\\
(y-x)(y+x)&=1
\end{aligned}
由 x,y > 1 可知,(y+x)>1。
所以方程无非零自然数解。
对于此结论,我们可以推出两个定理。
关于这两个定理的唯一性详见 Part\ 4。
\mathcal{Part\ 3}
本节讨论勾股数中出现偶数的情况。
首先我们暴力打表,发现当偶数为短直角边时,有以下数列满足。
4 3 5
6 8 10
8 15 17
10 24 26
……
容易发现,当另外两数 y,z 为 (\frac{x}{2})^2-1,(\frac{x}{2})^2+1 时,可以满足条件。
下面证明此结论。
设短直角边为 2n。
\begin{aligned}
b&=n^2-1\\
c&=n^2+1\\
a^2+b^2&=n^4+2n^2+1=(n^2+1)^2=c^2
\end{aligned}
由于 a,b,c>0,所以 n>1。
故大于 2 的所有偶数都有勾股数配对。
\mathcal{Part\ 4}
本节讨论组成勾股数的一般通项公式。
由 Part\ 1,Part\ 2 可知,任意大于 2 的自然数都可以组成勾股数。
那么当我们需要任意构造勾股数时,又该怎么办呢。
先给结论:
给出任意两个自然数 m,n,且 m>n,我们可以构造以下勾股数。
下面给出证明。
$$
\begin{aligned}
a^2+b^2&=(m^2-n^2)^2+(2mn)^2\\
&=m^4-2m^2n^2+n^4+4m^2n^2\\
&=m^4+2m^2n^2+n^4\\
&=(m^2+n^2)^2\\
&=c^2
\end{aligned}
$$
由此我们推导出了构造勾股三元组的一般公式。
不难看出,每一个三元组对应其唯一 $m,n$。
## $\mathcal{Part\ 5}
本节讨论互质勾股数。
互质勾股数,顾名思义,就是三元组中三个勾股数公因子为 1 的数。
当然,你也可以说成两两互质,这两个命题等价。
关于为什么等价,这里给出证明。
假设 a,b,c 是勾股数,则 a^2+b^2=c^2,
反设 a,b 不互质,有最大公约数 k(k>1),
则 c^2=a^2+b^2 一定有约数 k^2,
则 $a,b,c$ 有公约数 $k$($k>1$),$a,b,c$ 不互质。
所以勾股数中,只有“两两互质”,才能“三个互质”。
当“三个互质”时,一定“两两互质”。
------------
接着我们再看互质勾股数的通项公式。
在一般公式的基础上,我们仅需要再加一点限制条件:
**$n,m$ 互质,$n+m=$ 奇数。**
前者很好理解,对于后者,我们可以这样理解:
若 $m$ 和 $n$ 都是奇数,$a,b,c$ 就会全是偶数,不符合互质。
## $\mathcal{Part\ 6}
本节讨论反勾股定理。
大部分人只听到过勾股定理 a^2+b^2=c^2,可是我们还有另一个公式——反勾股定理。
如下:
\dfrac{1}{a^2}+\dfrac{1}{b^2}=\dfrac{1}{h^2}
其中 h 是斜边上的高。
给出证明。
$\therefore a^2+b^2=c^2$.
$\because ab=ch
得到 $(a^2+b^2)h^2=a^2b^2$.
$\therefore c^2h^2=a^2b^2,ch=ab$。
命题得证。
------------
当然,此公式也可用射影定理求证。
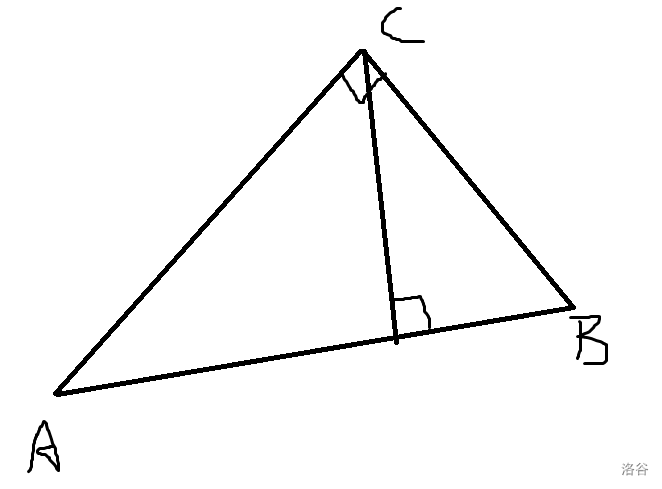
证明如下:
设斜边上的垂足为 $D$,则:
$$
\begin{aligned}
a^2&=BD\times c\\
b^2&=AD\times c\\
h^2&=BD\times AD\\
BD&=\frac{a^2}{c}\\
AD&=\frac{b^2}{c}\\
h^2&=BD\times AD = \frac{a^2}{c}\times \frac{b^2}{c}=a^2\times \frac{b^2}{c^2}\\
\frac{1}{h}&=\frac{c}{ab}=\frac{\sqrt{a^2+b^2}}{ab}=\sqrt{\frac{a^2+b^2}{a^2b^2}}=\sqrt{\frac{1}{b^2}+\frac{1}{a^2}}
\end{aligned}
$$
证毕。
------------
此公式在初中数学竞赛中应用较广,对于一些 $Rt.$ 三角形的题目,可以运用此公式。
## $\mathcal{Part\ 7}
本节讨论复数概念的勾股定理。
请注意,本节的勾股数并不一定是 \in \mathbb{Q} 的。
(此节由于作者太菜,基本是搬的,由于复数域的勾股比较重要)
一个实部与虚部皆为整数且皆不为零的复数,当与其共轭复数之积是一个完全平方数时,这个复数是勾股数。
任意一个复数 a+bi,必定存在 b-ai 与它垂直,以 a+bi 与 b-ai 的模长为边可作一直角三角形,这个直角三角形的斜边是一个复数,且这个斜边是由 a+bi 与 b-ai 的模唯一确定的。假定它是 c+di ,则 a+bi 的模长的平方与 b-ai 的模长的平方之和等于 c+di 的模长的平方,可以总结成下面这个公式。
\vert m(a+bi)\vert^2+\vert n(b-ai))\vert^2=\vert c+di\vert^2
此公式的所有字母都不得取零。
注意:只有像 a+bi 与 b-ai 这样的一对复数才满足勾股定理。在这里,a 和 b 是可以相等的,即 a+ai 与 a-ai 这样的一对复数也满足勾股定理。
对于任意一个复数 a+bi ,由于复数包括实数和纯虚数,因此,复数 a+bi 可以看成是复数 a 与复数 bi 的和。由于 a 和 bi 相互垂直,且 a 的模是 a,bi 的模是 bi,所以 a+bi 的模的平方等于 a 的模的平方加上 bi 的模的平方,即
\vert a\vert^2+\vert bi\vert^2=\vert a+bi\vert^2
上式表明,a+bi 的模的平方等于 a 的模的平方加 bi 的模的平方。
推导过程在此: (其中 norm 即为模运算)
\mathcal{Part\ 8}
本节讨论关于勾股数的一些小性质,小规律。
给出结论:三元组 \{a,b,c\} 之积一定可以被 60 整除,同时 \{a,b\} 之积一定能被 12 整除。
下面给出证明。
设 a^2+b^2=c^2。
首先判定 a,b 的奇偶性。
若 a,b 同为奇数,根据奇数的平方 \bmod\ 8=1 (证明在此),我们可知 (a^2+b^2)\bmod\ 8=2 。
而 c 必定为偶数,所以 c^2\bmod\ 4=0。
故 a,b 必不可能全是奇数,其中至少有一个是偶数。
分类讨论:
-
如果 a,b 都为偶数,则 ab\bmod\ 4=0。
-
当 a,b 有且仅有一个偶数,我们不妨设 b 为奇数。
首先 c 必为奇数。
那么 c^2-b^2=a^2,由于 c^2\equiv b^2(\bmod\ 8) ,则 a 为 4 的倍数。
综上,ab 必为 4 的倍数。
再设 a 为 3k+n(n\in \{0,1,2\})。
当 a 不是 3 的倍数时,显然 a^2\bmod\ 3 只能为 1。同理 b 亦是如此。
那么 (a^2+b^2)\bmod\ 3 只能为 2,而此时 c^2\bmod\ 3=1 或 0,这与原等式矛盾。
所以 ab 必为 3 的倍数。
又设 a 为 5k+n(n\in \{0,1,2,3,4\})。
当 a 不是 5 的倍数时,显然 a^2\bmod\ 5 只能为 1,4。同理 b,c 亦是如此。
那么 (a^2+b^2)\bmod\ 5 只能为 2,3,而此时 c^2\bmod\ 5=1 或 4,这与原等式矛盾。
所以 abc 必为 5 的倍数。
由以上三个定理我们可以推出:三元组 \{a,b,c\} 之积一定可以被 60 整除,同时 \{a,b\} 之积一定能被 12 整除。
\mathcal{Part\ 9}
本节讨论关于三维形式上的勾股定理,即德古阿定理。
我们考虑在一个正方体截取一个角锥。
如图黄色部分。
则有 S^2_{ABC}=S^2_{ABD}+S^2_{ACD}+S^2_{BCD}。
至此,本文结束。
或许作者在未来某个时候又一次看到了关于勾股的其他东西,还会来更。
不过那是后话了。
Good\ Bye!
Update on 2024.2.16:增加 part 9.