数列的极限
tiancai_1234
·
2023-12-24 00:09:00
·
个人记录
说在前面的话
这一章的内容是大家初学高数时都比较头疼的主题----极限。请拾起你的信心,和我一起学习这节内容,相信对于你理解数列极限会有很大的帮助。请耐心“品”完这节内容,以你的聪明才智肯定能搞定它。不过,如果你真正理解后不要急着离开,请再仔细过目一两遍,因为第一遍只是理解,第二遍第三遍甚至更多遍才能使你把极限定义的本质牢记于心!时隔多日你可能会生疏,那时最好再回过头来看看。希望大家看到支持我一下,记得关注我呦,让我们共同努力吧!虽然现在学业很忙,但是我会持续更新的呦~
1. 数列极限的定义
$\quad$ 设有一个圆,首先在园的里面放上一个正六边形,把正六边形的面积记作 $A_1$;再放一个正十二边形,再将面积记作 $A_2$;再放一个正二十四边形,把它的面积记作 $A_3$;以此类推,每次边数加倍,一般地,把正 $6\times 2^{n-1}$ 边形的面积记作 $A_n(n\in N_+)$。这样,就得到一系列正多边形的面积
$$A_1,A_2,A_3,...,A_n,...,$$
它们构成一列有次序的数。当 $n$ 越大,~~鱼越贵~~,正多边形与圆的差别就越小,从而以 $A_n$ 作为圆面积的近似值也就越精确。但是无论 $n$ 取得如何大,只要 $n$ 取定了, $A_n$ 终究只是多边形的面积,而还不是圆的面积。因此,设想 $n$ 无限增大(记作 $n\to\infty$,读作 $n$ 趋于无穷大),即正多边形的变数无限增加,在这个过程中,正多边形无限接近于圆,同时 $A_n$ 也无限接近于某一确定的数值,这个确定的数值也就理解为圆的面积。这个确定的数值在数学上称为上面这列有次序的数(所谓**数列**)$A_1,A_2,A_3,...,A_n,...$ 当 $n\to\infty$ 时的**极限**。在圆的面积问题中我们看到,正是这个数列的极限才精确地表达了圆的面积。
$\quad$ 在解决实际问题中逐渐形成的这种极限方法,已成为高数的一种基本方法,因此有必要做进一步的阐明。
$\quad$ 先说明数列的概念。如果按某一法则,对每个 $n\in N_+$,对应着一个确定的实数 $x_n$,这些实数 $x_n$ 按照下标 $n$ 从小到大排列得到的一个序列
$$x_1,x_2,x_3,...,x_n,...,$$
就叫做**数列**,简记为 $\{x_n\}$.
$\quad$ 数列中的每一个数叫做数列的**项**,第 $n$ 项 $x_n$ 叫做数列的**一般项**(或**通项**)。例如:
$$\frac{1}{2},\frac{2}{3},\frac{4}{3},...,\frac{n}{n+1},...;$$
$$2,4,8,...,2^n,...;$$
$$\frac{1}{2},\frac{1}{4},\frac{1}{8},...,\frac{1}{2^n},...;$$
$$1,-1,1,-1,...,(-1)^{n+1},...;$$
$$2,\frac{1}{2},\frac{4}{3},...,\frac{n+(-1)^{n-1}}{n},...$$
都是数列的例子,它们的一般项依次为
$$\frac{n}{n+1},2^n,\frac{1}{2^n},(-1)^{n+1},\frac{n+(-1)^{n-1}}{n}.$$
$\quad$ 在几何上,数列 $\{x_n\}$ 可看做数轴上的一个动点,它一次取数轴上的点 $x_1,x_2,x_3,..,x_n,...
$$x_n=f(n),n\in N_+$$
当自变量 $n$ 依次取 $1,2,3...$ 一切正整数时,对应的函数值就排列成数列 $\{x_n\}$。
$\quad$ 对于我们要讨论的问题来说,重要的是:当 $n$ 无限增大时(即 $n\to \infty$ 时),对应的 $x_n=f(n)$ 是否能无限接近于某个数值?如果能的话,这个数值等于多少?
$\quad$ 我们对数列
$$2,\frac{1}{2},\frac{4}{3},...,\frac{n+(-1)^{n-1}}{n},...\quad(2-1)$$
进行分析。在这数列中
$$x_n=\frac{n+(-1)^{n-1}}{n}=1+(-1)^{n-1} \frac{1}{n}.$$
$\quad$ 我们知道,两个数 $a$ 和 $b$ 之间的接近程度可以用这两个数的绝对值 $|b-a|$ 来度量(在数轴上 $|b-a|$ 表示点 $a$ 和点 $b$ 之间的距离), $|b-a|$ 越小, $a$ 和 $b$ 就越接近。
$\quad$ 就数列 $(2-1)$ 来说,因为
$$|x_n-1|=|(-1)^{n-1}\frac{1}{n}|=\frac{1}{n}$$
由此可见,当 $n$ 越来越大时,$\frac{1}{n}$ 越来越小,从而 $x_n$ 就越来越接近于 $1$。因为只要 $n$ 足够大,$|x_n-1|$ 即 $\frac{1}{n}$ 可以小于任意给定的整数,所以说,当 $n$ 无限增大时, $x_n$ 无限接近于 $1$。例如,给定 $\frac{1}{100}$,欲使$\frac{1}{n}<\frac{1}{100}$,只要 $n>100$,即从第 $101$ 项起,都能使不等式
$$|x_n-1|<\frac{1}{100}$$
成立。同样滴,如果给定 $\frac{1}{10000}$,那么从 $10001$ 项开始,都能使不等式
$$|x_n-1|<\frac{1}{100}$$
成立。一般地,不论给定的整数 $\epsilon$ 多么小,总存在一个正整数 $N$,使得当 $n>N$ 时,不等式
$$|x_n-1|<\epsilon$$
都成立。这就是数列 $x_n=\frac{n+(-1)^{n-1}}{n}(n=1,2,...)$ 当 $n\to\infty$ 时无限接近于 $1$ 这件事的实质。这样一个数 $1$,叫做数列 $x_n=\frac{n+(-1)^{n-1}}{n}(n=1,2,...)$ 当 $n\to\infty$ 时的**极限**。
$\quad$ 一般地,有以下数列极限的定义:
$\quad$ 定义:**设 $\{x_n\}$ 为一数列,如果存在常数 $a$,对于任何给定的整数 $\epsilon$(不论它多小),总存在正整数 $N$,使得当 $n>N$ 时,不等式**
$$|x_n-a|<\epsilon$$
**都成立,那么称整数 $a$ 是数列 $\{x_n\}$ 的极限,或者称数列 $\{x_n\}$** **收敛于** $a$,记为
$$\lim\limits_{n\to\infty}x_n=a,$$
或
$$x_n\to a(n\to \infty).$$
$\quad$ 如果说不存在这样的常数 $a$,就说数列 $\{x_n\}$ 没有极限,或者说数列 $\{x_n\}$ 是**发散**的。习惯上也说 $\lim\limits_{n\to\infty}x_n$ 不存在。
$\quad$ 上面定义中正数 $\epsilon$ 可以任意给定是重要的,因为只有这样,不等式 $|x_n-a|<\epsilon$ 才能表达出 $x_n$ 与 $a$ **无限接近**的意思。此外因还注意到:定义中的正整数 $N$ 是与任意给定的正数 $\epsilon$ 有关的,它随着 $\epsilon$ 的给定而给定。
$\quad$ 我们给“数列 $\{x_n\}$的极限为 $a$”一个几何解释:
$\quad$ 将常数 $A$ 及数列 $x_1,x_2,x_3,..,x_n,...$ 在数轴上用他们对应的点表示出来,再在数轴上作点 $a$ 的 $\epsilon$ 邻域,即[开区间](https://baike.baidu.com/item/%E5%BC%80%E5%8C%BA%E9%97%B4/9594680) $(a-\epsilon,a+\epsilon)$,如下图:
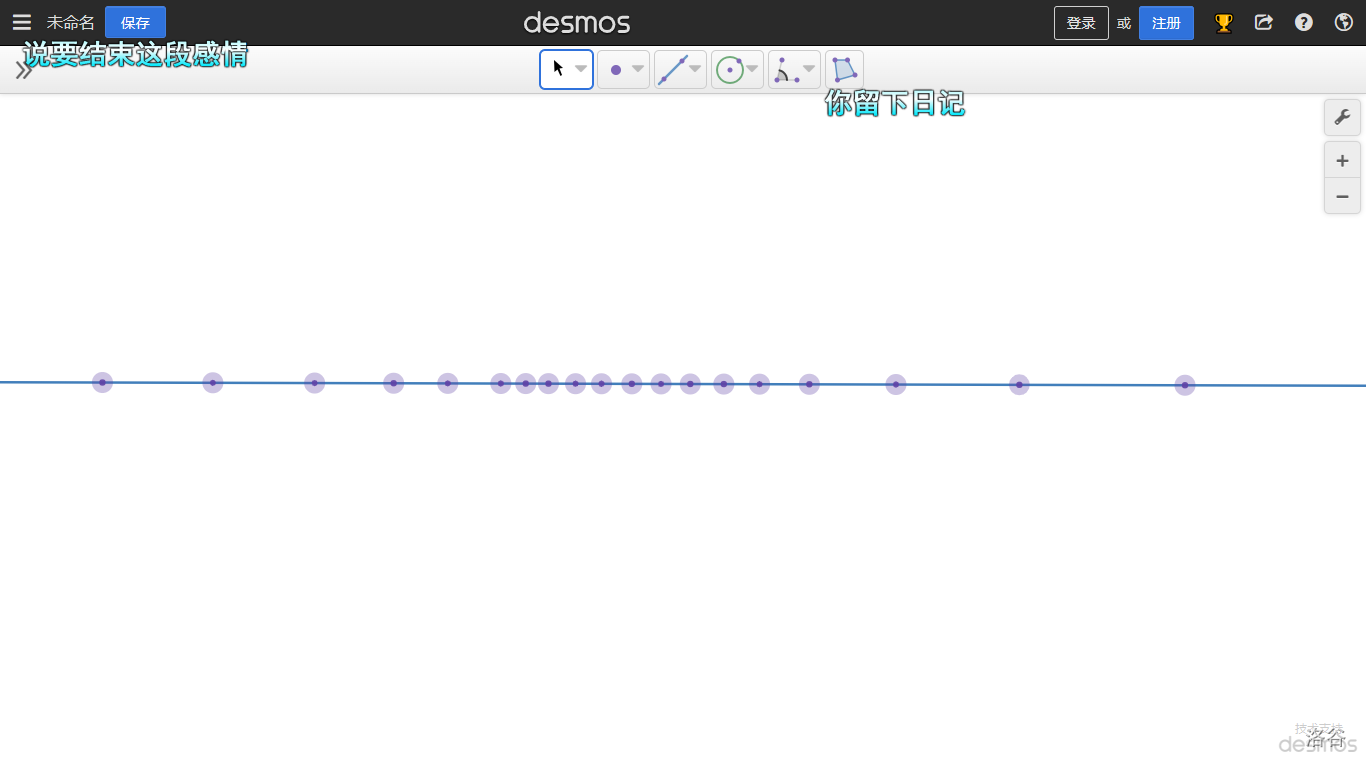
因不等式
$$|x_n-a|<\epsilon$$
与不等式
$$a-\epsilon<x_n<a+\epsilon$$
等价,所以当 $n>N$ 时,所有的点 $x_n$ 都落在开区间 $(a-\epsilon,a+\epsilon)$ 内,而只有有限个(至多有 $N$ 个)在这区间以外。
$\quad$ 为了表达方便,引入记号“$\forall$”表示“对于任意给定的”或“对于每一个”,浙大的苏德矿教授将它简称为“任给”,记作“$\exists$”表示“存在”。于是,“对于任给的 $\epsilon>0$”写成“$\forall \epsilon>0$”,“存在正整数 $N$”写成“$\exists$ 正整数 $N$”,数列极限 $\lim\limits_{n\to\infty}x_n=a$ 的定义可表达为
$\lim\limits_{n\to\infty}x_n=a\Leftrightarrow\forall \epsilon>0,\exists$ 正整数 $N$,当 $n>N$ 时,有 $|x_n-a|<\epsilon$.
$\quad$ 数列极限的定义并未直接提供如何去求数列的极限,以后再讲数列极限的求法,而现在先举几个说明极限概的例子。
1. 证明数列
$$2,\dfrac{1}{2},\dfrac{4}{3},...,\dfrac{n+(-1)^{n-1}}{n},...$$
的极限是 $1$。
证 $\quad$ $|x_n-a|=|\dfrac{n+(-1)^{n-1}}{n}-1|=\dfrac{1}{n}
这个 $\dfrac{1}{\epsilon}$ 是一个确定的实数,而对于任何一个实数都有无穷多个大于它的正整数存在。所以,任取一个大于 $\dfrac{1}{\epsilon}$ 的正整数作为 $N$,例如,取 $N=[\dfrac{1}{\epsilon}]+1$,则当 $n>N$ 时,就有
$$|\dfrac{n+(-1)^{n-1}}{n}-1|<\epsilon,$$
即
$$\lim\limits_{n\to\infty}\frac{n+(-1)^{n-1}}{n}=1$$
2. 已知 $x_n=\dfrac{(-1)^n}{(n+1)^2}$,证明数列 $\{x_n\}$ 的极限是 $0$.
证 $\quad$ $|x_n-a|=|\dfrac{(-1)^n}{(n+1)^2}-0|=\dfrac{1}{(n+1)^2}<\dfrac{1}{n^2}.
\forall \epsilon>0$,为了使 $|x_n-a|<\epsilon$,只要$\dfrac{1}{n^2}<\epsilon$ 或 $n>\dfrac{1}{\sqrt{\epsilon}},
这个 \dfrac{1}{\sqrt{\epsilon}} 是一个确定的实数,大于 \dfrac{1}{\sqrt{\epsilon}} 的正整数有无穷多个存在,任取其中一个作为 N ,例如,取 N=[\dfrac{1}{\sqrt{\epsilon}}]+1 ,则当 n>N 时,就有
|\dfrac{(-1)^n}{(n+1)^2}-0|<\epsilon,
即
\lim\limits_{n\to\infty}\dfrac{(-1)^n}{(n+1)^2}=0.
注意! \quad 在利用数列极限的定义来论证某个数 a 是数列 \{x_n\} 的极限时,重要的是对与任意给定的整数 \epsilon ,要能够指出定义中所说的这种正整数 N 确实存在。如果知道 |x_n-a| 小于某个量(这个量与 n 存在函数关系),那么当这个量小于 \epsilon 时,|x_n-a|<\epsilon 当然也成立。若令这个量小于 \epsilon 能推出符合定义要求的正整数 N 必定存在,就可采用这种方法。例 2 便是这样做的。当然,在利用极限定义证明极限时,如果能具体找出一个满足定义要求的正整数 N ,那么也就证明了这种 N 的存在。在以后的证明中,多采取这种找出一个符合要求的正整数 N 的方法。
设 |q|<1 ,证明等比数列
1,q,q^2,...,q^{n-1},...
的极限是 0 。
证 \quad \forall\epsilon>0( 设 \epsilon<1) ,因为
|x_n-0|=|q^{n-1}-0|=|q|^{n-1},
要使 |x_n-0|<\epsilon ,只要
|q|^{n-1}<\epsilon
取自然对数,得 (n-1)\ln|q|<\ln\epsilon 。因 |q|<1,\ln|q|<0 ,故
n>1+\dfrac{\ln\epsilon}{\ln|q|},
取 N=\begin{bmatrix}1+\dfrac{\ln\epsilon}{\ln|q|} \end{bmatrix} ,则当 n>N 时,就有
|q^{n-1}-0|<\epsilon,
即
\lim\limits_{n\to\infty}q^{n-1}=0.
收敛数列的性质
下面四个定理都是有关收敛数列的性质。
定理1(极限的唯一性)\quad 如果数列 \{x_n\} 收敛,那么它的极限唯一。
证 \quad 用反证法。假设同时有 x_n\to a 及 x_n\to b ,且 a<b 。取 \epsilon=\dfrac{b-a}{2} 。因为 \lim\limits_{n\to\infty}x_n=a ,故 \exists 正整数 N_1 ,当 n>N_1 时,不等式
|x_n-a|<\dfrac{b-a}{2}\quad (2-2)
都成立。同理,因为 \lim\limits_{n\to\infty}x_n=b ,故 \exists 正整数 N_2 ,当 n>N_2 时,不等式
|x_n-b|<\dfrac{b-a}{2}\quad (2-3)
都成立。取 N=\max\{N_1,N_2\} (这式子表示 N 是 N_1 和 N_2 中较大的那个数),则当 n>N 时,(2-2) 式及 (2-3) 式会同时成立,但由 (2-2) 式有
4. 证明数列 $x_n=(-1)^{n+1}(n=1,2,...)$ 是发散的。
证 $\quad$ 如果这数列收敛,根据定理 $1$ 它有唯一的极限,设极限为 $a$,即$\lim\limits_{n\to\infty}x_n=a$。按数列极限的定义,对于 $\epsilon=\dfrac{1}{2}$,$\exists$ 正整数 $N$ ,当$n>N$ 时,$|x_n-a|<\dfrac{1}{2}$ 成立;即当 $n>N$ 时,$x_n$ 都在开区间 $\begin{pmatrix}a-\dfrac{1}{2},a+\dfrac{1}{2}\end{pmatrix}$ 内。但这是不可能的,对于 $n\to \infty$ 时,$x_n$ 无休止地一再重复取得 $1$ 和 $-1$ 这两个数,而这两个数不可能同时属于长度为 $1$ 的开区间$\begin{pmatrix}a-\dfrac{1}{2},a+\dfrac{1}{2}\end{pmatrix}$ 内。因此这数列发散。
$\quad$ 由函数有界性的概念可得以下的数列有限性概念。
$\quad$ 对于数列 $\{x_n\}$,如果存在正数 $M$,使得对一切 $x_n$ 都满足不等式
$$|x_n|\leqslant M$$
那么称数列 $\{x_n\}$ 是**有界的**;如果这样的正数 $M$不存在,就说数列 $\{x_n\}$ 是**无界的**。
$\quad$ 例如,数列 $x_n=\dfrac{n}{n+1}(n=1,2,...)$ 是有界的,因为可取 $M=1$,而使
$$|\dfrac{n}{n+1}|\leqslant 1$$
对于一切正整数 $n$ 都成立。
$\quad$ 数列$x_n=2^n(n=1,2,...)$ 是无界的,因为当 $n$ 无限增加是时,$2^n$ 可超过任何正数。
$\quad$ 数轴上对应于有界数列的点 $x_n$ 都落在某个区间 $[-M,M]$ 上。
**(收敛数列的有界性)$\quad$ 如果数列 $\{x_n\}$ 收敛,那么数列 $\{x_n\}$ 一定有界。**
证 $\quad$ 因为数列 $\{x_n\}$ 收敛,设 $\lim\limits_{n\to\infty}x_n=a$。根据数列极限的定义,对于 $\epsilon=1$,$\exists$ 正整数 $N$,当 $n>N$ 时,不等式
$$|x_n-a|<1$$
都成立。于是,当 $n>N$ 时,
$$|x_n|=|(x_n-a)+a|\leqslant|x_n-a|+|a|<1+|a|.$$
取 $M=\max\{|x_1|,|x_2|,...,|x_N|,1+|a|\}$,那么数列 $\{x_n\}$ 中的一切 $x_n$ 都满足不等式
$$|x_n|\leqslant M.$$
这就证明了数列 $\{x_n\}$ 是有界的。
$\quad$ 根据上述定理,如果数列 $\{x_n\}$ 无界,那么数列 $\{x_n\}$ 一定发散。但是,如果数列 $\{x_n\}$ 有界,却不能**断定**(注意是断定)数列 $\{x_n\}$ 一定收敛,例如数列
$$1,-1,1,...,(-1)^{n+1},...$$
有界,但例 $4$ 证明了这数列是发散的。所以数列有界是数列瘦脸的必要条件,但不是充分条件。
**定理3(收敛数列的保号性)$\quad$ 如果 $\lim\limits_{n\to\infty}x_n=a$,且 $a>0($ 或 $a<0)$,那么存在的正整数 $N$,当 $n>N$ 时,都有 $x_n>0($ 或 $x_n<0)$。**
证 $\quad$ 就 $a>0$ 的情形证明。由数列极限的定义,对 $\epsilon=\dfrac{a}{2}>0$,$\exists$ 正整数 $N$,当 $n>N$ 时,有
$$|x_n-a|<\dfrac{a}{2}.$$
从而
$$x_n>a-\dfrac{a}{2}=\dfrac{a}{2}>0.$$
$\quad$ **推论 $\quad$ 如果数列 $\{x_n\}$ 从某项起有 $x_n\geqslant 0($ 或 $x_n<0)$。**
证 $\quad$ 设数列 $\{x_n\}$ 从第 $N_1$ 项起,即当 $n>N_1$ 时有 $x_n\geqslant0$。现在用反证法证明。若 $\lim\limits_{n\to\infty}x_n=a<0$。则由定理 $3$ 知,$\exists$ 正整数 $N_2$,当 $n>N_2$ 时,有 $x_n<0$。取 $N=\max\{N_1,N_2\}$,当 $n>N$ 时,按假定有 $x_n\geqslant0$,按定理 $3$ 有 $x_n<0$ 的情形,这引起矛盾。所以必有 $a\geqslant 0$。
$\quad$ 数列 $\{x_n\}$ 从某项起有 $x_n\leqslant0$ 的情形,可以类似地证明。
$\quad$ 最后,介绍子数列的概念以及关于收敛数列与其子数列间关系的一个定理。
$\quad$ 在数列 $\{x_n\}$ 中任一抽取无限多项并保持这些项在原数列 $\{x_n\}$ 中的先后次序,这样的到的一个数列称为原数列 $\{x_n\}$ 的**子数列**(或**子列**)(其实有点像高中的子集)。
$\quad$ 设在数列 $\{x_n\}$ 中,第一次抽取 $x_{n1}$,第二次抽取 $x_{n2}$,第三次在 $x_{n2}$ 后抽取 $x_{n3}......$ 这样无休止地抽取下去,得到一个数列
$$x_{n1},x_{n2},x_{n3},...,x_{nk},...,$$
这个数列 $\{x_{nk}\}$ 就是数列 $\{x_n\}$ 的一个子数列。
**注意!**$\quad$ 在子数列 $\{x_{nk}\}$ 中,一般项 $x_{nk}$ 是第 $k$ 项,而 $x_{nk}$ 在原数列 $\{x_n\}$ 中却是第 $n_k$ 项,显然,$n_k\geqslant k$。
**定理4(收敛数列与其子数列间的关系)$\quad$ 如果数列 $\{x_n\}$ 收敛于 $a$,那么它的任一子数列也收敛,且极限也是 $a$。**
证 $\quad$ 设数列 $\{x_{nk}\}$ 是数列 $\{x_n\}$ 的任一子数列。
$\quad$ 由于 $\lim\limits_{n\to\infty}x_n=a$,故 $\forall\epsilon>0$,$\exists$ 正整数 $N$,当 $n>N$ 时,$|x_n-a|<\epsilon$ 成立。
$\quad$ 取 $K=N$,则当 $k>K$ 时,$n_k>n_K=n_N\geqslant N$。于是 $|x_n-a|<\epsilon$。这就证明了 $\lim\limits_{n\to\infty}x_n=a$。证毕。
$\quad$ 由定理 $4$ 可知,如果数列 $\{x_n\}$有两个子数列收敛于不同的极限,那么数列 $\{x_n\}$ 是发散的。例如,例 $4$ 中的数列
$$1,-1,1,...,(-1)^{n+1},...$$
的子数列 $\{x_{2k-1}\}$ 收敛于 $1$,而子数列 $\{x_{2k}\}$ 数列于 $-1$,因此数列 $x_n=(-1)^{n+1}(n=1,2,...)$ 是发散的。同时这个例子也说明,一个发散的数列也有可能有收敛的子数列。
大家可以做一下下面几题:
求数列 $\{\dfrac{1}{2^n}\},\{(-1)^n\dfrac{1}{n}\},\{2+\dfrac{1}{2^n}\}$ 那些数列发散?那些收敛?
本文结!
后语:本文参考《高等数学》同济八版第一章第二节。
感兴趣的同学可以看一下[这里](https://zhuanlan.zhihu.com/p/256419158)