树状数组合集
zzx0102
·
·
算法·理论
声明一下:这里没有可持久化树状数组是因为我太菜,而不是做不了,想看的可以去看最后一篇参考资料。
我永远喜欢树状数组。
前置知识:线段树。
1. 基础树状数组:
引入问题:P3374 【模板】树状数组 1
显然如果直接暴力一定会 T,考虑优化。
考虑将这些区间拆分成更少的区间数,再对区间暴力求和,就可以起到优化的作用。
于是考虑任何一个数 x 在二进制下均只有 \mathcal{O}(\log x) 位为 1。
于是,我们考虑将 [1,x] 这个区间拆分成 \mathcal{O}(\log x) 个区间的和。
令 x=2^{d_1}+2^{d_2}+\cdots +2^{d_k},且 \forall i\in[2,k],d_i>d_{i-1},设 s_i=s_{i-1}+2^{d_i},s_0=0,则 [1,x] 被我们拆分成了 \bigcup\limits_{i=1}^k(s_{i-1},s_i]。
例:当 x=15 时,x=(1111)_2,即 [1,x]=(0,8]\cup(9,12]\cup(12,14]\cup(14,15]。
我们用 \operatorname{lbt}(x) 表示 \operatorname{lowbit}(x),指 x 在二进制中最低位的 1 的值,即当 x=2^{d_1}+2^{d_2}+\cdots 2^{d_k} 时,\operatorname{lbt}(x)=2^{\min\limits_{i=1}^k d_i}。
所以一般的树状数组大致长这样:
考虑这样分有一个性质:对于每一个区间的右端点 r,都只对应一个 l。
首先,根据我们的拆分规则,r=l+2^x,并且 x=\log_2\operatorname{lbt}(r),所以 l=r-\operatorname{lbt}(r)。
所以一共有 n 个不同的子区间。
接下来快速维护 n 个子区间。
由于 n 个区间的右端点各不相同,所以每个区间的区间和可以标记在右端点的位置上。考虑建立一个数组 tr,则 tr_x 表示以 x 为右端点的子区间的和。即
tr_x=\sum\limits_{i=x-\operatorname{lbt}(x)+1}^{x} a_x
其中 a_x 表示单点值。
接下来考虑如何修改和查询。
查询显然直接每次将 x 减去 \operatorname{lbt}(x),每次累加 tr_x,直至 0 就完事了,复杂度 \mathcal{O(\log x)}。
考虑如何修改。
修改其实也不难,考虑修改 x 即将所有包含 x 的区间都求出来。
考虑 tr_{x+\operatorname{lbt}(x)} 这个区间包含 x。
然后 tr_{x+\operatorname{lbt}(x)+\operatorname{lbt}(x+\operatorname{lbt}(x))} 包含 x+\operatorname{lbt}(x),也包含 x。
所以每次将 x 加上 \operatorname{lbt}(x),一直到 n 即可。
到了这里,已经可以写出修改和查询的代码了。
void chg(int x, int k) {for(; x <= n; x += lbt(x)) tr[x] += k;}
int ask(int x) {int sum = 0; for(; x; x -= lbt(x)) sum += tr[x]; return sum;}
这里有一个常数优化,可以使树状数组查询常数变小。
考虑查 [l,r] 的区间和,那么可以用前缀和的方式去求,这当中会有一些重复计算。忽略这些重复计算即可优化。
int ask(int l, int r){
l--; int sum = 0;
while(r > l) sum += a[r], r -= lbt(r);
while(l > r) sum -= a[l], l -= lbt(l);
return sum;
}
大约快了一倍。
于是考虑如何求 \operatorname{lbt}(x)。
这个总不能 \mathcal{O}(\log n) 枚举,不然复杂度会多一个 \log。
当然您可以考虑预处理 \forall i\in[1,n],\operatorname{lbt}(i),不过这样就显得有些没有技术含量,而且会使树状数组常数增大。
计算机用补码存储和表示数值。考虑 -x(x > 0)的补码,它等于 x 的反码 +1。设 \mathrm{lbt}(x) = 2 ^ k,我们发现 -x 的补码在低 k - 1 位(第 0\sim k - 1 位)都是 0;在第 k 位和 x 相同,均为 1;在高于 k 的位和 x 相反。
例如,对于二进制数 (0\cdots 010100)_2,其 \operatorname{lowbit} 值为 4,其反码为 (1\cdots 101011)_2,相反数的补码为 (1\cdots 101100)_2。又因为正数的补码就是它本身,所以一个数的 \operatorname{lowbit} 值就等于它和它的相反数的按位与,即 x & -x。
P3374 CODE
接下来,考虑如何用树状数组维护区间加区间和。
这里使用差分。设差分数组为 d,原数组为 a。则
a_i=\sum\limits_{j=1}^i d_j
区间查询即
\sum\limits_{i=l}^r a_i
=\sum\limits_{i=l}^r\sum\limits_{j=1}^i d_j
考虑计算贡献,得原式为
\sum\limits_{i=1}^{l-1} (r-l+1)d_i+\sum\limits_{i=l}^r (r-i+1)d_i
=\sum\limits_{i=1}^{l-1} (r-l+1)d_i+(r+1)\sum\limits_{i=l}^r d_i- \sum\limits_{i=l}^r d_i\times i
=(r+1)\sum\limits_{i=1}^{l-1}d_i-l\times \sum\limits_{i=1}^{l-1}d_i+(r+1)\sum\limits_{i=l}^r d_i- \sum\limits_{i=l}^r d_i\times i
=(r+1)\sum\limits_{i=1}^r d_i-l\times \sum\limits_{i=1}^{l-1} d_i- \sum\limits_{i=1}^r d_i\times i+\sum\limits_{i=1}^{l-1} d_i\times i
考虑用两个树状数组维护 d_i 以及 d_i\times i 的前缀和,直接计算即可。
P3372 CODE
二维树状数组:
在以为数组上直接加一维即可。
注意这里加入和修改传入的第二维变量不能直接作为循环变量,否则第二次循环时这个变量被永久改变了,就只能修改第一行。
那么如何处理矩形加矩形和的问题呢?
考虑直接将上面的差分沿用过来即可,维护四个树状数组,分别表示 d_{i,j},d_{i,j}\times i,d_{i,j}\times j,d_{i,j}\times i\times j。
P4514 CODE
树状数组也可以 \mathcal{O}(n) 建树,就是利用类似于 DP 的思想刷新后面的。
for(int i = 1; i <= n; i++) if(i + lbt(i) <= n) tr[i + lbt(i)] += a[i];
2.权值树状数组及其进阶
考虑维护一个数据结构:
- 插入 x 数
- 删除 x 数(若有多个相同的数,应只删除一个)
- 查询 x 数的排名(排名定义为比当前数小的数的个数 +1 )
- 查询排名为 x 的数
- 求 x 的前驱(前驱定义为小于 x,且最大的数)
- 求 x 的后继(后继定义为大于 x,且最小的数)
离散化后值域为 [1,n]。
考虑维护一个树状数组去解决。
我们令这个桶叫作 t。
加入一个数:即 t_x\gets t_x+1。
删除一个数:即 t_x\gets t_x-1。
查询排名:\sum\limits_{i=1}^{x-1}t_i+1 即为答案。
查询排名为 x 的数:
令 x 的排名为 f(x)
考虑求 \max\limits_{f(k)\le x}k 即为所求答案,得
\sum\limits_{i=1}^k t_i\le x-1
看上去可以二分,但是这样复杂度变成 \mathcal{O}(n\log^2 n),不太行。
考虑在树状数组上倍增,令当前位置是 p,和是 s。
考虑不断将 p 往后跳,如果跳过去排名仍然小于 x 就直接跳,否则就啥都不干。
举个例子,比如目前加入了 8 个数 \{1,2,3,4,5,6,7,8\},并且 p=0,s=0。
则树状数组 tr=\{1,2,1,4,1,2,1,8\},查询排名为 5 的数。
考虑将 p 向后跳 2^3 到 p=8 处,则 s\gets s+tr_p=0+8>5,不行。
接下来将 p 向后跳 2^2 到 p=4 处,则 s\gets s+tr_p=0+4<5,可行,此时 p=4,s=4。
然后将 p 向后跳 2^1 到 p=6 处,则 s\gets s+tr_p=4+2>5,不可行。
最后将 p 向后跳 2^0 到 p=5 处,则 s\gets s+tr_p=4+1=5,不可行。
所以最后答案为 p+1=5。
前驱和后继可以用操作 1,2,3,4 组合一下求出。
总复杂度 \mathcal{O(n\log n)}。
P3369 CODE
您也可以用类似的方法实现 区间 MEX 问题。
考虑直接对整个序列像 HH 的项链那样直接扫描线,然后同样在树状数组上倍增。
不过这个树状数组不属于本文讲的权值树状数组。
练习:P3224 [HNOI2012] 永无乡
这里介绍一下树状数组合并。
考虑用 pbds 哈希表实现动态开点树状数组。
由于树状数组具有可以整体相加的性质,所以合并两棵树状数组时,直接将这两个哈希表启发式合并一下即可。
启发式合并是指合并两个数据结构时,把少的合并到多的上,考虑每一个元素,它每被合并一次,所在堆的大小至少是原来的两倍。
这里每个节点合并最多合并 \log n 次,总共 n\log w 个节点,所以复杂度 \mathcal{O(n\log w\log n)},第 y 小可以使用权值树状数组解决。
P3224 CODE
习题:P9176 [COCI2022-2023#4] Vrsta
这种水题大家一定都会,这里不做介绍。
权值树状数组其实也是可以实现树套树的。
考虑我们已经写好了动态开点树状数组。
由于两棵树状数组满足整体加减的性质,所以将一般的权值线段树换成权值树状数组即可。复杂度 \mathcal{O}(n\log ^2 n)。
P3380 CODE
3. 树状数组维护不可差分信息
以最大区间子段和为例,$tr_x$ 表示 $[x-\operatorname{lbt}(x)+1,x]$ 的区间最大子段和
那么每一段都要维护:
$sum$ 区间和,后面有用。
$lmax$,左半边的区间最大子段和。
$rmax$,右半边的区间最大子段和
$ans$,区间最大子段和。
那么一次合并操作,合并两个区间 $[l_1,r_1]$ 和 $[l_2,r_2]$,要求 $l_1\le r_1+1=l_2\le r_2$。
$sum$ 即为两端区间和。
$lmax$:可以考虑选 $[l_1,r_1]$ 的 $lmax$,也可以选整段 $[l_1,r_1]$ 和 $[l_2,r_2]$ 的 $lmax$。
$rmax$:同理要么选 $[l_2,r_2]$ 的 $rmax$,也可以选整段 $[l_2,r_2]$ 和 $[l_1,r_1]$ 的 $rmax$,
$ans$:即为 $[l_1,r_1]$ 的 $ans$ 或 $[l_2,r_2]$ 的 $ans$,也可以是 $[l_1,r_1]$ 的 $rmax$ 与 $[l_2,r_2]$ 的 $lmax$ 拼接而成。
~~所以考虑线段树上进行合并区间操作。~~
令 $\operatorname{merge}(a,b)$ 表示合并 $a,b$ 区间后的四个值。
令 $\operatorname{Max}(x,y)$ 表示 $x$ 到 $y$ 的维护区间最大子段和的四个值,然后树状数组叫做 $tr$,$tr_x=\operatorname{Max}(x-\operatorname{lbt}(x)+1,x)$。
考虑查询,查询时当 $y-\operatorname{lbt}(y)>x$ 时,之间用 $tr_y$ 更新。$\operatorname{Max}(x,y)=\operatorname{Merge}(\operatorname{Max}(x,y-\operatorname{lbt}(y)),tr_y)$。
否则,就开始单点的暴力查询,令 $w_x$ 为 $x$ 的单点值。
$$\operatorname{Max}(l,r)=\operatorname{merge}(\operatorname{Max}(l,r-1),w_r)$$
这是因为需要访问单点值,所以这种方法只支持单点修改。
单点修改呢?
设修改 $x$ 变为 $k$。
其实就是先把 $w_x$ 设成 $k$,然后从 $x$ 开始,到 $x+\operatorname{lbt}(x),x+\operatorname{lbt}(x)+\operatorname{lbt}(x+\operatorname{lbt}(x))\cdots$ 都用 $\log$ 的复杂度暴力修改。
这样做复杂度 $\mathcal{O}(n\log^2 n)$,虽然线段树可以 $\mathcal{O}(n\log n)$,但是 BIT 常数小无伤大雅。而且这么写码量小。
当然你也可以用类似的方法求区间最值,不过这样显得很落后时代。
[P4513 CODE](https://www.luogu.com.cn/paste/dizm38oz)
$\mathcal{O}(\log n)$ 做法:
以区间 $\min$ 为例:
我们考虑建立两颗树状数组,其中 $tr2_x$ 表示 $\min\limits_{i=x-\operatorname{lbt}(x)+1}^x a_x$,$tr1_x$ 表示 $\min\limits_{i=x}^{\operatorname{lbt}(x)+x-1} a_x$。
考虑如何查询 $\min\limits_{i=l}^r a_i$。
注意到这个 $\min$ 是不可差分信息,所以必须覆盖整个区间的信息并且不重不漏,任何区间范围超出了查询范围都是不可取的。
所以考虑直接在 $tr1$ 上爬树,爬到右端点大于 $y$ 为止,再从 $tr2$ 上爬树,爬到左端点小于 $x$ 为止。
然后发现中间有可能有一段区间没有覆盖到,暴力查询即可。
不难发现中间这一段的长度非常小。
我们以区间 $[5,13]$ 为例:
首先,在 $tr1$ 上爬树,分别访问 $tr1_{13},tr1_{12}$,而 $tr1_8$ 的覆盖范围是 $[1,8]$,超出了 $[5,13]$,所以不能取。
然后在 $tr2$ 上爬树,访问 $tr2_{5},tr2_{6}$,$tr2_8$ 的覆盖范围是 $[8,15]$,超过了范围,依旧不能取。
不难发现此时查询覆盖了 $[5,7]$ 和 $[9,13]$ 的最小值,暴力查 $[8,8]$ 即可。
结论:剩下的区间最多只有一个数。
证明:假设
$$
l=(c_1c_2\cdots c_x 0l_1l_2\cdots l_n)_2\\
r=(c_1c_2\cdots c_x 1r_1r_2\cdots r_n)_2\\
k=(c_1c_2\cdots c_x 100\cdots0)_2
$$
$c$ 表示 $l$ 和 $r$ 前半段二进制相同的部分。
我们从 $l$ 开始往后枚举的时候,必然会枚举到 $k$,$tr2_k$ 对应的区间右端点显然不小于 $r$,所以从 $l$ 开始向后枚举可能只能枚举到 $[l,k)$ 这一段。
同理,我们从 $r$ 向前枚举的时候,也必然会枚举到 $k$,所以从 $r$ 开始向前枚举,所以从 $r$ 开始向前枚举只能枚举到 $(k,r]$ 这一段。
那么只有 $k$ 可能枚举不到,单独更新 $a_k$ 即可。
复杂度 $\mathcal{O}(q\log n)$。
修改:
这里只考虑单点修改,即对于一个位置 $p$ 和值 $v$,将 $a_p$ 修改为 $v$($v$ 和 $a_p$ 的大小关系未知)。
有一种方法,就是在两棵树上从 $p$ 开始向上爬树,这样可以搞出来所有含 $p$ 的节点 $u$ 对应的区间 $[x,y]$,将 $u$ 对应的值改成 $[x,p)$、$(p,y]$ 和 $v$ 的最小值即可,但是这样复杂度就变成了 $O(\log^2n)$ 了,这要是能比线段树快就过于逆天了。
单 $\log$:
对于区间 $[x,p-1]$ 和 $[p+1,y]$,他们都有一个端点是定值。
有一个结论:对于树 $BIT1$ 来说,$u$ 的父亲一定是 $u+1$ 或 $u+1$ 的祖先。
证明:如果 $u$ 是奇数,$u$ 的父亲是 $u+lbt_u=u+1$。
如果 $u$ 是偶数,那么 $u+1$ 是奇数。
还是令
$$
u=(u_1u_2u_3\cdots u_{x}100\cdots0)_2\\
u+1=(u_1u_2u_3\cdots u_{x}100\cdots1)_2
$$
并且 $lbt_u=2^k$,显然 $k>0$。
$u$ 的父亲是 $u+lbt_u=u+2^k$。
$u+1$ 的父亲是 $(u+1)+1=u+2^1$。
从 $u+1$ 开始爬树,会爬到 $u+2^1,u+2^2,u+2^3,\cdots,u+2^k$,所以必然会爬到 $u$ 的父亲。
同理,对于树 $BIT2$ 来说,$u$ 的父亲一定是 $u-1$ 或 $u-1$ 的祖先。
这样我们可以从 $p+1$ 开始爬 $BIT1$,把爬到的节点 $y$ 时经过的所有节点的最小值都记录下来,就是 $[p+1,y]$ 的最小值。
同理我们可以从 $p-1$ 开始爬 $BIT2$,可以得到 $[x,p-1]$ 的最小值。
这样我们就可以把答案记录下来,再从 $p$ 开始爬树得到包含 $p$ 的区间 $[x,y]$,这样我们已经预处理过了 $[x,p-1]$ 和 $[p+1,y]$ 的最小值了,就可以单次 $O(1)$ 更新。
这样我们可以在 $O(q\log n)$ 的复杂度内用树状数组完成单点修改区间查询不可差分信息。
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
#define I inline
#define gc getchar
#define DISABLE_MMAP
const int N = 10000010, inf = 2e9;
int a[N], n, q;
int tr1[N], tr2[N];
I int read() {
int x = 0, f = 1; char ch = gc();
while(ch < '0' || ch > '9') {if(ch == '-') f = -f; ch = gc();}
while(ch >= '0' && ch <= '9') x = x * 10 + (ch ^ 48), ch = gc();
return x * f;
}
I int query(int x, int y) {
if(x > y) return inf;
int u = x, mi = inf;
while(u + (u & -u) <= y) {
mi = min(tr2[u], mi);
u += u & -u;
}
int k = u;
mi = min(mi, a[k]);
u = y;
while(u - (u & -u) >= x) {
mi = min(tr1[u], mi);
u -= u & -u;
}
return mi;
}
int p1[N], p2[N];
int main() {
long long ans = 0;
n = read(), q = read();
for(int i = 1; i <= n; i++) a[i] = read(), tr1[i] = tr2[i] = a[i];
for(int i = 1; i <= n; i++) {
int j = i + (i & -i);
if(j <= n) tr1[j] = min(tr1[j], tr1[i]);
}
for(int i = n; i; i--) {
int j = i - (i & -i);
tr2[j] = min(tr2[j], tr2[i]);
}
for(int i = 1; i <= q; i++) {
int o = read(), x = read(), y = read();
if(o == 1) {
int u = x + 1, mi = inf;
while(u <= n) {
p1[x] = min(tr1[x], mi);
mi = min(mi, tr1[x]);
u += u & -u;
}
u = x - 1;
while(u) {
p2[x] = min(tr2[x], mi);
mi = min(mi, tr2[x]);
u -= u & -u;
}
u = x;
while(u <= n) {
tr1[u] = min({p2[u - (u & -u) + 1], p1[u], y});
u += u & -u;
}
u = x;
while(u) {
tr2[u] = min({p2[u], p1[u + (u & -u) - 1], y});
u -= u & -u;
}
a[x] = y;
}
else {
ans ^= 1ll * query(x, y) * i;
}
}
cout << ans;
return 0;
}
```
[P3865 CODE](https://www.luogu.com.cn/paste/ajmr67l4)
## 4. 树状数组实现懒标记
如果说我们像维护线段树那样子直接在树状数组上每个节点维护懒标记的话,每次 pushdown 就需要传递 $\mathcal{O}(\log n)$ 个节点,复杂度就会退化成 $\mathcal{O}(\log ^2n)$,不太行。
我们可以对每个节点和它们右边的空白位置都建立一个延迟标记,就像下面这幅图。
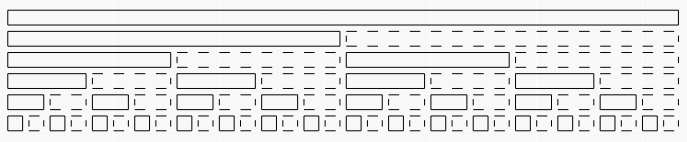
实线矩形表示原树状数组,在所有矩形(包括实线矩形和虚线矩形)内都要维护懒标记。
考虑修改。
对刚好覆盖到的区间直接修改和并且维护懒标记,对于没有完全覆盖的区间直接修改一下,由于深度越大的节点代表的区间长度越小,所以要类似于倍增,自底向上暴力爬树。
查询类似于线段树,边走边 pushdown,但是注意最后需要正常查询。
这个东西类似于线段树,但是相较于线段树有不少优点:
1. 空间小,线段树需要 $8n$ 的数组维护,而树状数组只需要 $3n$。
2. 常数小,线段树需要递归,而树状数组只用位运算。
3. 码量略小于线段树。
[P3372 CODE](https://www.luogu.com.cn/paste/cu242ehq)
加上参考资料里面的可持久化 BIT,至此我们已经基本完成了用树状数组代替线段树。
参考资料:
<https://ioi.te.lv/oi/files/volume9.pdf#page=41>
<https://www.luogu.com.cn/blog/388651/about-RBIT>
<https://www.luogu.com.cn/blog/countercurrent-time/qian-tan-shu-zhuang-shuo-zu-you-hua>