记本次 GESP 八级
leo120306
·
·
个人记录
提示:本文没有正解!!!
总体来说海星。
首先是选判题,这次还是挺简单的。几何题只考了勾股定理 ,不会三角函数的六年级生狂喜。代数题套一下组合数和二项式的公式就行了。语法算法题也还行。
重头戏当然是编程题。我先把自己回忆的题面放一下(可能与原题有出入,但不影响理解)。
题面
T1
给定一棵 n 个节点的无根树(无边权),每个节点是黑色或白色,求这棵树中相距最远的不同色节点的距离。
另外 $30$%:$n\le 10^3$。\
所有:$n\le 10^5$。
## T2
给定一个二维平面,上面有 $n$ 个水平于 $x$ 轴的挡板。第 $i$ 个挡板的左端点 $x$ 坐标为 $l_i$,右端点 $x$ 坐标为 $r_i$,$y$ 坐标为 $h_i$。保证所有挡板两两无交点。你初始在第 $s$ 个挡板的左端点处,目标是移到第 $t$ 个挡板上。在挡板上左右移动 $1$ 单位需要 $1$ 秒。当你在挡板的左右端点时,你可以下坠直到下面的挡板(下坠过程中不能左右移动)。下坠 $1$ 单位同样需要 $1$ 秒。求最短时间花费,无解输出 $-1$。
$20$%:对于所有 $1\le i\le n$,$l_i=1$。\
另外 $40$%:对于所有 $1\le i\le n$,$l_i=i,r_i=i+1$。\
所有:$n\le 10^3,1\leq l_i\leq r_i \leq 10^5,1\leq h_i \leq 10^5$。
# 思路
## T1
容易发现我太弱了。我想不出正解,就先把 Task 2 打了暴力。从每个点开始广搜记录答案,时复 $O(n^2)$。
然后是 Task 1,链式图只需要从两头开始搜就行了,时复 $O(n)$。
不过我还不知道正解。好像比较接近的是只搜叶子节点?不过最坏时复依然是 $O(n^2)$(菊花图)。好像又有点像要求 LCA 的节奏,不过又不完全像 ~~(我连 LCA 的板子都没背)~~。知道正解/场上拿满的 dalao 可以告诉我一下 qwq。
后面想着随机化拼人品骗 Task 3(GESP 可以 $32$ 次测试),然后 Task 3 拿到了 $0pts$ 的好成绩。
考场上 $15pts$(即 $25pts\times 60\%$),拿了前两个部分分。
## T2
好像要 dp,但我连状态都不会设,一看部分分有 $15pts$,果断地去骗部分分了。
### Solution 0
学习⑨,输出 $-1$。\
预计得分 $0-25pts$。\
考场实测 $7.5pts$,~~比我旁边那个辛辛苦苦打了半天的老哥还高 2.5pts hhh~~。
### Solution 1
首先有一个好想的无解情况:$h_s\leq h_t$,毕竟你总不可能往上跳或者跨过空隙吧。\
那么排除这种情况,我们直接去想 Task 1。既然所有挡板左端点都在 $1$,开局直接从左端点跳下去就行了。到达第 $t$ 个挡板的左端点只需要 $h_s-h_t$ 秒。答案即为 $h_s-h_t$。
剩下情况,传承⑨的优良品德,输出 $-1$。
预计得分 $5-25pts$。\
考场实测 $10pts$,~~看来对 CCF 来说,学习⑨还是有用的。~~
### Solution 2
在 Solution 1 的基础上,我们拼命地想 Task 2。\
容易发现 Task 2 有解的前提是 $h_s$ 至 $h_t$ 单调(严格)递减,因为你只能往下跳。\
那么有解的情况答案是怎样的呢?画一张图:(可能有点丑,见谅)
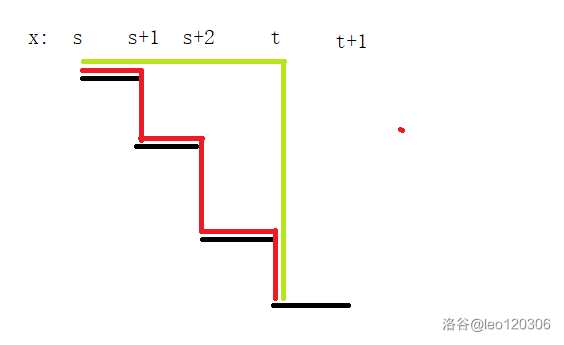
红线是实际要走的路径。把它们移补一下就变成了等长的绿线。我们发现,绿线的长度就是 $t$ 与 $s$ 的差加上上下高度差!形式化地说,答案为 $t-s+h_s-h_t$。
剩下情况,继续传承⑨的优良品德,输出 $-1$。
预计得分 $15-25pts$。\
考场实测 $15pts$,~~看来对 CCF 来说,有时学习⑨是没用的。~~
考场上实现了 Solution 2,得到 $15pts$(即 $25pts\times 60\%$),同样拿了前两个部分分。
有 dalao 知道正解吗 qwq。
## 总结
挺难的。现在编程题已经扣 $20pts$ 了,选判再扣一下就会 $80$ 不保。当然 $60$ 是稳的。
**暑假真的来了,祝大家暑假快乐!**
奶嘴可爱捏,所以奶嘴来镇文了。$↓