Lyndon & Runs
command_block
2021-01-17 17:14:56
读者可能需要前往 [Border理论小记](https://www.luogu.com.cn/blog/command-block/border-li-lun-xiao-ji) 学习相关知识，否则可能无法理解某些内容。
本文包含的内容 ：
- Lyndon 分解
- Lyndon 树 （未完）
- The Runs Theorem
- 本原平方串 primitive square
参考资料 ：
- `WC2019` 课件《The Runs Theorem and Lyndon Tree》。
- [《The “Runs” Theorem》- 2014](https://xueshu.baidu.com/usercenter/paper/show?paperid=1s6n0x702n350an09g5808q0wc380925&site=xueshu_se)
其中，前者的部分内容是后者的翻译。
# 0. 初步的定义 & 约定
字符串一般记为小写字母，确定的字符用 $\texttt{abcdef}$ 字体表示，单独的不定字符用 $\overline a$ 表示。
对于字符串 $s$ ，有如下概念。
- **长度** ：记为 $|s|$ ，在针对单串集中的讨论中也约定为 $n$。（ 本节下面一律有 $n=|s|$ ）
- **字符** ：用 $s[i]$ 表示串 $s$ 的第 $i$ 个字符。$s$ 中的字符标号为 $1,2,\dots,n$。
单个字符也被视作字符串。
- **字符集** ： 记为 $\Sigma_s$ 。
为了简化边界条件，若取到标号在 $[1,n]$ 之外的字符，定义其不在字符集内。
- **字符串的比较** ： 若 $s$ 的字典序比 $t$ 小，记为 $s<t$。
若字符串集合 $D$ 中的所有串都小于 $s$ ，记为 $D<s$。
类似地有 $\leq ,>,\geq $。
- **子串** ： $s[l,r]$ 表示将 $s[l],s[l+1],\dots,s[r]$ 顺次连接而成的字符串。
- **前缀&后缀** ： 简记 $s\langle i]=s[1,i],\ s[i\rangle=s[i,n]$。（注意里面填的是位置而非长度）
称一个前缀/后缀为严格的，当且仅当它 $≠$ 原串 $s$。
记 ${\rm pre}(s)$ 为 $s$ 的前缀集合， ${\rm suf}(s)$ 为 $s$ 的后缀集合。
记 ${\rm pre}'(s)$ 为 $s$ 的严格前缀集合， ${\rm suf}'(s)$ 为 $s$ 的严格后缀集合。
- **出现位置** ： 对于串 $t$ ，记：
${\rm Beg}_s(t)$ 为 $t$ 在 $s$ 中所有出现位置的左端点集合。
${\rm End}_s(t)$ 为 $t$ 在 $s$ 中所有出现位置的右端点集合。
对于区间集合 $L$ ，类似地记 ：
${\rm Beg}(L)$ 为 $L$ 的左端点集合。
${\rm End}(L)$ 为 $L$ 的右端点集合。
- **字符串的拼接，幂** ： 记 $st,\ s\cdot t$ 为字符串 $s,t$ 顺次连接而得的串。
定义 $s^k=\overbrace{ss\dots s}^{\text{共 k 个}}$ ，即 $s$ 重复 $k$ 次后形成的串。
- **循环节** $\bf period$ ： 若对于所有 $1\leq i\leq n-c$ ，均有 $s[i]=s[i+c]$ ，则称 $c$ 是 $s$ 的一个循环节。
若 $c|n$ 则称 $c$ 为整周期。
记 ${\rm period}(s)$ 为 $s$ 的循环节集合。
- **$\bf Border$** ： 若有 $s\langle i]=s[n-i+1\rangle\ (1\leq i<n)$（等于后缀的**严格**前缀），则称之为 $\rm Border$ ，简称为 $\rm Bd$。
记 ${\rm Bd}(s)$ 为 $s$ 的 $\rm Bd$ 集合。（ 注意 $s\not\in {\rm Bd}(s)$ ）
$\rm Bd$ 和 $\rm period$ 是一一对应的。其中，一个长度为 $k$ 的 $\rm Bd$对应一个长度为 $n-k$ 的循环节。
- **$\bf Lyndon\ Word$** ： 若字符串 $s$ 的最小后缀是其本身，即 $s<{\rm suf}'(s)$ ，则称之为 $\rm Lyndon Word$ ，简称为 $\rm Ly$。
另一个等价的定义 ： $s$ 是自己的所有循环位移中最小的一个。
例 ： $\texttt{abc,ababc}$ 是 $\rm Ly$，而 $\texttt{ba,acabc}$ 不是。
- **$\bf Runs$** ： 三元组 ${\bf r}=(l,r,p)$ 是串 $s$ 的一个 $\rm run$ ，当且仅当 ：
- $s[l,r]$ 的**最小**循环节为 $p$ ，满足 $2p\leq \big|s[l,r]\big|=r-l+1$
- 该循环不能延伸，即 $s[l-1]≠s[l+p-1],s[r+1]≠s[r-p+1]$
实数 $e_{{\bf r}}=\dfrac{r-l+1}{p}$ 被称为该 $\rm run$ 的指数。
记 ${\rm Runs}(s)$ 为 $s$ 的所有 $\rm run$ 构成的集合。
$ρ_{\rm run}(n)$ 表示长度为 $n$ 的字符串中至多含有的 $\rm run$ 个数。
$σ_{\rm run}(n)$ 表示长度为 $n$ 的字符串的 $\rm run$ 的指数和的最大值。
为了方便，上面的约定了一些不正规的缩写，相信大家很容易就能感性理解。（逃）
# 1. Lyndon Word 的性质
在不能理解证明的时候，建议画图。在一些关键的地方我也会制作图示。
- $\color{blue}\bf\Delta$ **定理(1.1)** : 对于任意一个 ${\rm Ly}\ s$ ，其不存在 $\rm Bd$。
若存在某个 ${\rm Bd}\ t$，则显然 $t<s$ ，同时 $t$ 又是 $s$ 的严格后缀，和 $\rm Ly$ 的定义矛盾。
- $\color{blue}\bf\Delta$ **定理(1.2)** : 对于 ${\rm Ly}\ s=ab$ ，有 $a<b$。（$a,b$ 均非空）
由定义有 $ab<b$ ，且显然有 $a<ab$ ，所以 $a<b$。
- **引理(1.1)** ： 若 $a$ 不是 $b$ 的前缀，则 $ac_1<bc_2\Leftrightarrow a<b$。证明较为显然，从略。
- $\color{blue}\bf\Delta$ **定理(1.3)** : 对于 ${\rm Ly}\ b$ 和另一个串 $a$， 有 $a<b\Leftrightarrow ab<b$
由 **引理(1.1)** ，若 $a$ 不是 $b$ 的前缀 ，则结论成立。
现在针对 $\rm Ly$ 来证明 $a$ 恰为 $b$ 前缀的情况。令 $b=at$。
显然有 $a<b$ ，所以必要性不必证明。
假设 $at=b<ab$ ，则有 $t<b$ ，由于 $t$ 是 $b$ 的一个后缀，这违反 $\rm Ly$ 的定义，矛盾。
- $\color{blue}\bf\Delta$ **定理(1.4)** : $s$ 是 $\rm Ly$ **当且仅当** $s=ab$，$a<b$ 且 $a,b$ 均为 $\rm Ly$。（$a,b$ 均非空，$|s|\geq 2$ ）
这个定理告诉我们，$\rm Ly$ 总是由两个更小的 $\rm Ly$ 按字典序拼成的。
- **充分性** ： $\big(a<b$ 且 $a,b$ 均为 ${\rm Ly}\big)\Rightarrow\big(ab$ 是 $\rm Ly\big)$。
$ab$ 的严格后缀可以分为 ${\rm suf}'(a)b,\ b,\ {\rm suf}'(b)$ 两个部分。
由 $a<{\rm suf}'(a)$ ，显然有 $ab<{\rm suf}'(a)b$。
由 **定理(1.3)** 有 $ab<b<{\rm suf}'(b)$ ，证毕。
- **必要性** ： $\big(s$ 是 ${\rm Ly}\big)\Rightarrow \big($ 存在 $i$ 使得 $s\langle i-1]<s[i\rangle$ 且 $s\langle i-1],s[i\rangle$ 均为 $\rm Ly\big)$。 （证明较为复杂，可暂时跳过）
找出 $s$ 的最小严格后缀 $s[i\rangle$。
- Part1. 由 **定理 (1.2)** 即可得到 $s\langle i-1]<s[i\rangle$。
- Part2. $s[i\rangle$ 为 $\rm Ly$
由最小严格后缀，不存在其他严格后缀比它还小，所以其是 $\rm Ly$。
- Part3. $s\langle i-1]$ 为 $\rm Ly$
假设前缀 $s\langle i-1]$ 存在长为 $k$ 的 $\rm Bd$。显然 $k+1<i$。
由最小严格后缀，可得 $s[k+1\rangle>s[i\rangle$，又因为 $s[1,k]=s[i-k,i-1]$ ，在这两个串后面分别接上不等式中的串，则有 $s>s[i-k\rangle$ ，与 $\rm Ly$ 的定义矛盾。所以， $s\langle i-1]$ 没有 $\rm Bd$。
对于 $1<j\leq i-1$ ，考虑 $s\langle i-1]s[i\rangle=s<s[j\rangle=s[j,i-1]s[i\rangle$。
由 **引理(1.1)** ，因为 $s\langle i-1]$ 无 $\rm Bd$ ，即 $s[j,i-1]$ 不是 $s\langle i-1]$ 的前缀，可得 $s[j,i-1]>s\langle i-1]$ ，则 $s\langle i-1]$ 是 $\rm Ly$。
- $\color{blue}\bf\Delta$ **定理(1.5)** : 若字符串 $s$ 和字符 $\overline x$ 满足 $s\overline x$ 是某个 $\rm Ly$ 的前缀，则对于 $\overline y>\overline x$ ，$s\overline y$ 是 $\rm Ly$。
设 $s\overline xt$ 是 $\rm Ly$ ，考虑 $1<j\leq |s|$。
若 $s[j\rangle \overline x$ 是 $s$ 的前缀，则由 $s[j\rangle \overline x<s[j\rangle \overline y$ （两者互不为前缀）使用 **引理(1.1)** 能导出 $s\overline y<s[j\rangle \overline y$。
若 $s[j\rangle \overline x$ 不是 $s$ 的前缀，考虑 $s[j\rangle \overline xt>s\overline xt$ ，使用 **引理(1.1)** 替换后面的东西，即得 $s[j\rangle \overline y>s\overline y$ 。
综上，总有 $s\overline y<s[j\rangle \overline y$ ，证毕。
- $\large\color{blue}\bf\circledast$ **定义** : 串的 $\rm Lyndon$ 分解
将字符串 $s$ 分解成 $s_1,s_2\dots s_m$ ，满足 $s_1,s_2,\dots,s_m$ 均为 $\rm Ly$ ，且 $s_1\geq s_2\geq \dots\geq s_m$。
- $\color{blue}\bf\Delta$ **定理(1.6)** : $\rm Ly$ 分解唯一
假设 $s$ 有两种 $\rm Ly$ 分解 ： $s=s_1s_2\dots s_i\dots s_m$ 且 $s=s_1's_2'\dots s_i'\dots s_m'$。
设 $i$ 为第一个满足 $s_i≠s_i'$ 的，不妨设 $|s_i|>|s_i'|$ ，且 $s_i=s_i's_{i+1}'...s_k's_{k+1}'\langle j]$。
有 $s_i<s_{k+1}'\langle j]\leq s_{k+1}'\leq s_{k}'\leq ...\leq s_i'<s_i$ ，矛盾。
- $\color{blue}\bf\Delta$ **定理(1.7)** : $\rm Ly$ 分解必然存在
开始时将 $s$ 分解为 $n$ 个串，每个串都只有一个字符。显然，单字符都是 $\rm Ly$。
接下来，若相邻的两个串满足 $s_i<s_{i+1}$ ，则合并。由 **定理(1.4)**，合并后仍是 $\rm Ly$。
容易发现，合并不会一直进行下去，停止时得到的就是 $\rm Ly$ 分解。
# 2. 求 Lyndon 分解 ： Duval 算法
前面在证明 $\rm Ly$ 分解存在性时，已经给出了一个构造，不过时间复杂度还不能令人满意。
不难发现，对于串 $s$ ，其唯一 $\rm Ly$ 后缀即为其最小后缀。每次取出最小后缀即可得到 $\rm Ly$ 分解。
这可以利用后缀数组求解，不过这样太复杂了。
接下来介绍 $\rm Duval$ 算法，其可以在 $O(n)$ 的时间内算得一个串的 $\rm Ly$ 分解。且代码实现非常简短。
其思想是 ： 不断求一个串的最长 $\rm Ly$ 前缀。
- $\color{blue}\bf\Delta$ **定理(2.1)** : 设 $s=u^ku'\overline a$ ，其中 $u$ 是 $\rm Ly$ ，$u'$ 是 $u$ 的严格前缀，$\overline a$ 是某个字符，且 $≠u\big[|u'|+1\big]$（接不上 $u$ 的循环）。
- ① 若 $\overline a>u\big[|u'|+1\big]$ ，根据 **定理(1.5)** ，这说明 $u'\overline a$ 是 $\rm Ly$ 。
由于此时 $u<u'\overline a$ ，可以将前面的 $t^c$ 全都合并。所以 $s$ 已经是一个 $\rm Ly$ 串。
- ② 若 $\overline a<u\big[|u'|+1\big]$ ，所有以 $s$ 开头的字符串，最长 $\rm Ly$ 前缀是 $u$。
若选择 $u^ku'$ 的长度大于 $|u|$ 的前缀，则会产生 $\rm Bd$ ，矛盾。
若选择 $u^ku'\overline a t$，由于 $u'\overline a$ 不是 $u$ 的前缀，使用 **引理(1.1)** 可得 $u'\overline a <u\Rightarrow u'\overline a t<u^ku'\overline a t$ ，则显然不是 $\rm Ly$。
.$\rm Duval$ 算法的主要过程是，在字符串中不断迭代，并不断保持 **定理(2.1)** 的形式。
维护两个指针 $p,i$ ，其中 $s[1,p-1]$ 的分解已经确定 ，$s[p,i]$ 是目前的一段待定串。
维护 $s[p,i]$ 的 $\rm Ly$ 循环，设 $s[p,i]=u^cu'$，其中 $t$ 是一个 $\rm Ly$ 串，$u'$ 是 $u$ 的严格前缀。需要维护 $|u|,c,|u'|$。
当加入字符 $s[i+1]$ 时 ：（若 $k+1>n$ 则 $s[k+1]=-∞$）
- ① $s[i+1]=s[i-|u|+1]$ ： 这说明目前的 $\rm Ly$ 循环可以延续下去。
- ② $s[i+1]>s[i-|u|+1]$ ： 根据 **定理(2.1)** ，$s[p,i+1]$ 为 $\rm Ly$，也是新的 $u$。
- ③ $s[i+1]<s[i-|u|+1]$ ： 根据 **定理(2.1)** ，此时的最长 $\rm Ly$ 前缀是 $u$ ，我们在确定的分解中加入 $c$ 个 $u$ ，然后令 $i$ 回到新的 $p$ 处重来。
不难发现， $i+p$ 总是递增。①② 中仅有 $i$ 增加，③ 中由于 $|u'|<|u^k|$ 所以 $p$ 的增加量大于 $i$ 的减少量。
所以，算法的时间复杂度为 $O(n)$。
- $\color{green}\bf\Delta$ **模板** ： [P6114 【模板】Lyndon 分解](https://www.luogu.com.cn/problem/P6114)
```cpp
#include<cstring>
#include<cstdio>
char s[5005000];
int main()
{
scanf("%s",s+1);
int n=strlen(s+1);
int p=0,i=1,u=1,c=1,u2=0,ans=0;
for (;i<=n;i++){
if (s[i+1]==s[i-u+1]){
u2++;
if (u2==u){c++;u2=0;}
}
else if (s[i+1]>s[i-u+1]){
u=i+1-p; u2=0; c=1;
}
else if (s[i+1]<s[i-u+1]){
for (int t=1;t<=c;t++)
{p+=u;ans^=p;}
i=p; u=1; c=1; u2=0;
}
}printf("%d",ans);
return 0;
}
```
[评测记录](https://www.luogu.com.cn/record/45097847)
- **扩展应用**
可以利用 $\rm Duval$ 算法求出 $s$ 的每个前缀的最小/最大后缀。
还可以求 $s$ 的最小表示，即求出最小的 $T=S[i\rangle S\langle i-1]$。
令 $s'=s+s$ ，求出 $s'$ 的 $\rm Ly$ 分解，找到起始位置 $\leq |s|$ 且最小的 $\rm Ly$ 串，即为最小表示的开头。
先咕了。
- $\color{green}\bf\Delta$ **例题** ：
- [HDU6761 Minimum Index](http://acm.hdu.edu.cn/showproblem.php?pid=6761) （模板）
- [CF594E Cutting the Line](https://www.luogu.com.cn/problem/CF594E) | [Sol] ()
# 3. Runs 的性质 : The Runs Theorem
- $\color{blue}\bf\Delta$ **定理(3.1)** : 两个周期为 $p$ 的 $\rm run$ 的交长度 $<p$。
若交的长度 $\geq p$ ，在交中选出一个循环节扩展，能导出矛盾。
- $\large\color{blue}\bf\circledast$ **定义** : $\rm run$ 的 $\text{Lyndon Root}$ （简称为 $\rm LyRoot$）
令 ${\bf r}=(l,r,p)$ 是串 $s$ 的一个 $\rm run$ 。
一个长为 $p$ 的区间 $[i,j]$ 被称为 $\rm LyRoot$ ，当且仅当 $s[i,j]$ 是 $\rm Ly$ ，且 $l\leq i\leq j\leq r$。
也就是说，$\rm LyRoot$ 是 $\rm run$ 的**循环节**中最小的那些。
显然，对于任意的一个 ${\bf r}$ ，其至少有一个 $\rm LyRoot$ （循环节的最小表示）。且所有 $\rm LyRoot$ 代表的串相等（只是位置不同）。
- $\color{blue}\bf\Delta$ **定理(3.2)** : $\text{The Runs Theorem} : ρ_{\rm run}(n)<n,σ_{\rm run}(n)\leq 3n-3$
证明是一段漫长的旅程，请诸位耐心跋涉。路虽艰远，行之必达。
下面的定理理解跨度较大，叙述有些碎片化，正如不完整的拼图那样，让人一时摸不着头绪。
但在拼图完整的那一刻，将会呈现优美的宏观结构，此时就能更清晰的洞察 ： 每一块拼图都有其意义和解释。
- $\large\color{blue}\bf\circledast$ **定义** : 字典序重载
对于 $\Sigma$ 中的一个全序关系 $<$ ，可以定义出字典序 $<$。
假设有 $\Sigma$ 中两种相反的全序关系 $<_0,<_1$ ，可以定义出两种相反的字典序 $<_0,<_1$。你可以认为 $<_0$ 就是普通的字典序。
为了避免矛盾，在字符串比较时，我们自动在串后面填充无限个占位符 $\texttt{\textdollar} \not\in \Sigma$。
对于 $\overline a\in\Sigma$ 约定 $\texttt{\textdollar}<_0\overline a$ （普通字典序中空位最小），$\overline a<_1\texttt{\textdollar}$ （反字典序中空位最大）
对于不同的字典序比较方法，可以定义出不同的 $\rm Ly$。
对 $f\in\{0,1\}$ ，记 $\neg f=1-f$。
- $\large\color{blue}\bf\circledast$ **定义** : 对于串 $s$，定义 ${\rm Ly}_{s,f}(i)=[i,j]$ 其中 $j=\max\{j|s[i,j]\text{是关于}<_f\text{的}{\rm Ly}\}$
也就是说，在 $<_f$ 意义下，串 $s$ 中起始位置为 $i$ 的最长的 $\rm Ly$ 子串。
- $\color{blue}\bf\Delta$ **定理(3.3)** : 对于${\rm Ly}_{s,f}(i)$，有且仅有一个 $f\in\{0,1\}$ 使得 ${\rm Ly}_{s,f}(i)=[i,i],{\rm Ly}_{s,\neg f}(i)=[i,j]\ (j>i)$
也就是说，正反两种字典序之中，只有一个能导出非平凡 $\rm Ly$ 子串。
令 $k=\min\{k|s[k]≠s[i],k>i\}$ （第一个不同字符，由于串末有 $\texttt{\textdollar}$ ，必然能找到），找出 $f$ 满足 $s[k]<_fs[i]$。
由 **定理(2.1)** ，不难得到 ${\rm Ly}_{s,f}(i)=[i,i]$ ,以及 ${\rm Ly}_{s,\neg f}(i)=[i,j],j\geq k>i$（已经有 $s[i,k]$ 作为 $\rm Ly$ 前缀）。
- $\color{blue}\bf\Delta$ **定理(3.4)** : 令 ${\bf r}=(l,r,p)$ 是串 $s$ 的一个 $\rm run$ ，找出 $f\in\{0,1\}$ 满足 $s[r+1]<_fs[r+1-p]$，则 $r$ 的所有关于 $<_f$ 的 ${\rm LyRoot}\ λ=[i,j]$ 都与 ${\rm Ly}_{s,f}(i)$ 相等。
我们知道 $\rm LyRoot$ 就是 ${\bf r}$ 的 $\rm Ly$ 循环节，设一个循环节为 $u$ ，将 $s[l,r]$ 写作 $u^ku'$ ，其中 $u'$ 是 $u$ 的一个严格前缀。
不难发现，该定理就是 **定理(2.1)** 的体现。
由 **定理(3.3)** ，如果使用 $<_{\neg f}$ ，那么总有 ${\rm Ly}_{s,\neg f}(i)=[i,i]$ ，没多大意义。
因此，$f$ 有其特殊性，记 $<_f$ 为 ${\bf r}$ 的“正序”。
- $\large\color{blue}\bf\circledast$ **定义** : 对于 ${\rm run}\ {\bf r}=(l,r,p)$，记 ${\rm LyR}({\bf r})=\{λ=[i,j]\big|λ\text{为}{\bf r}\text{的关于}<_f\text{的}{\rm LyRoot},i≠l\}$，其中 $f$ 是 ${\bf r}$ 的正序。
即 ${\rm LyR}({\bf r})$ 表示 $r$ 的所有正序的 $\rm LyRoot$ ，但要除去开头位置 $l$ 出开始的（如果有的话）。
显然 $|{\rm LyR}({\bf r})|\geq \lfloor e_{\bf r}-1\rfloor\geq 1$。
- $\color{blue}\bf\Delta$ **定理(3.5)** : 对于串 $s$ 的两个不同的 ${\rm run}\ {\bf r}=(l,r,p),{\bf r}'=(l',r',p')$ ，有 ${\rm Beg}({\rm LyR}({\bf r}))∩{\rm Beg}({\rm LyR}({\bf r}'))=\varnothing$。
假设存在 $i\in {\rm Beg}({\rm LyR}({\bf r}))∩{\rm Beg}({\rm LyR}({\bf r}'))$ ，且有 ${\rm LyRoot}\ λ=[i,j]\in{\rm LyR({\bf r})},\ λ=[i,j']\in{\rm LyR({\bf r}')}$
令 $<_f$ 为 ${\bf r}$ 的正序，则 $λ={\rm Ly}_{s,f}(i)$ 。
不难发现一定有 $λ≠λ'$ （ $λ=λ'\Rightarrow {\bf r}={\bf r}'
$ ），所以只能是 $λ'={\rm Ly}_{s,\neg f}(i)$。
由 **定理(3.3)** ，$λ,λ'$ 必有一个为 $[i,i]$ ，不妨设 $λ=[i,i]$ ，则有 $j'>i$。
由于 $s[i,j']$ 是 $\rm Ly$ ，所以 $s[i]≠s[j']$ 。
由 **定理(3.4)** 可知，$r$ 的循环节 $p=|λ|=1$ ， $r'$ 的循环节 $p'=|λ'|=j'-i+1$。
由 ${\rm LyR}(r)$ 的定义，$r,r'$ 的左端点都 $<i$。
由周期性可推得 $s[i]=s[i-1]=s[i-1+(j'-i+1)]=s[j']$ ，矛盾。证毕。
**定理(3.5)** 表明，$\rm run$ 们拥有两两不交的非空集合 ${\rm Beg}({\rm LyR}({\bf r}))$，而且 $1$ 不在其中，所以我们已经能够证明 $ρ_{\rm rum}(n)<n$。
进一步写出 $\sum\limits_{{\bf r}\in {{\rm Runs}(s)}}|{\rm LyR}({\bf r})|\leq n-1$。
由 $e_{\bf r}-2\leq \lfloor e_{\bf r}-1 \rfloor\leq |{\rm LyR}({\bf r})|$ ，得 $\sum\limits_{{\bf r}\in {{\rm Runs}(s)}}e_{\bf r}-2\leq \sum\limits_{{\bf r}\in {{\rm Runs}(s)}}|{\rm LyR}({\bf r})|\leq n-1$
结合 $|{\rm Runs}(s)|\leq n-1$ ，即可得到 $σ_{\rm run}(n)\leq 3n-3$
至此，我们证明了 **定理(3.2)** $\text{The Runs Theorem}$。
- **扩展** ： $ρ_{\rm run,k}(n)<n/(k-1)$ ，其中 $ρ_{\rm run,k}$ 指指数达到 $k$ 的 $\rm run$ 的个数。
若某个 ${\rm run}\ {\bf r}$ 的指数达到 $k$ ，则 $|{\rm LyR}({\bf r})|\geq k-1$，利用 $\sum\limits_{{\bf r}\in {{\rm Runs}(s)}}|{\rm LyR}({\bf r})|\leq n-1$ 不难证明。
# 4. Runs 相关计算
在一些不必区分不同字典序的地方，会略去字典序参数 $f$。
- $\color{green}\bf\Delta$ **模板** ：[Loj#173. Runs](https://loj.ac/p/173)
- 找出 ${\rm Runs}(s)$ ： 暴力《优秀的拆分》
先枚举周期 $p$ ，在原串中每隔 $p$ 个位置撒一个关键点，一个 $\rm run$ 必然穿过至少两个关键点。
对相邻的两个关键点向前向后求 $\rm LCP$ ，若覆盖范围能连接，则找到一个可能的 $\rm run$。
可以利用 **定理(3.1)** 进行剪枝。
当然，目前枚举的周期 $p$ 不一定就是当前 $\rm run$ 的最小周期，所以需要按照 ${\bf r}=(l,r,p)$ ，中的 $(l,r)$ 分类，每个类中保留一个 $p$ 最小的即可。
若使用字符串 $\rm Hash$ 实现，复杂度为 $O(n\log^2n)$，可以使用后缀数组做到 $O(n\log n)$。
$O(n\log^2n)$ ：[评测记录](https://loj.ac/s/1040596) （ 能获得 $80'$，不剪枝只能得 $60'$ ）
- 计算所有的 ${\rm Ly}_{s}(i)$
维护每个后缀的 $\rm Ly$ 分解 $s_1s_2\dots s_m$，取出 $s_1$ 即可得到 ${\rm Ly}_{s}(i)$。这需要不断向前加字符。
先将字符 $\overline c$ 当作一个 $\rm Ly$ 串插入到分解开头，然后若分解中 $s_1<s_2$ 则不断合并。正确性显然。
也就是说，我们只需要支持比较两个串的字典序，这可以随便 $\rm Hash$ 一手搞定。
更进一步地，根据 **定理(1.3)** 以及 **引理(1.1)** ，$s_1<s_2\Leftrightarrow s_1s_2<s_2\Leftrightarrow s_1s_2\dots s_m<s_2\dots s_m$
这就是说，我们把两个相邻 $\rm Ly$ 串的比较转化成了后缀的比较。这可以简化代码实现。
- 找出 ${\rm Runs}(s)$ ：利用性质
由 **定理(3.3)** ，一个 $\rm run$ 所含有的 $\rm Ly$ 循环节一定是某个字典序下某个后缀的最长 $\rm Ly$ 前缀。显然，两个不同的 $\rm run$ 不可能包含同一个循环节。
利用此条性质，我们可以不必暴力枚举循环节了，可选的循环节为 $O(n)$ 个，分别前后求 $\rm LCP$ 即可。
形式化地，枚举 $l,f$ ，对于 ${\rm Ly}_{s,f}(l)=[l,r]$，求出最长的 $l_1,l_2$ 使得 $s[l,l+l_1-1]=s[r,r+l_1-1],s[l-l_2,l-1]=s[r-l_2,r-1]$
若 $l_1+l_2\geq r-l+1$ ，我们就找到了一个 ${\rm run}\ (l-l_2,r+l_1-1,r-l+1)$。
如图，两段绿色部分相等，一段紫色是一个 $\rm Ly$ 循环节。
$l_1+l_2\geq r-l+1$ 即要求绿色部分能连接起来，显然这是充要条件。
最终仍然要去重。
实现时，简便的 $\rm Hash$ 算法是个不错的选择。
$O(n\log n)$ : [评测记录](https://loj.ac/s/1041208) （有点卡常数，单模`const`了才过）
你可能对上述算法有这样的疑问 ：$\rm Lyndon$ 串和字典序有关，$\rm Runs$ 只和匹配有关，为什么求 $\rm Runs$ 的算法对 $\rm Ly$ 理论有非常强的依赖性呢？
其实，$\rm Ly$ 串只是用于在循环串中确定一个最小循环节（某种意义上构造了映射），以简化求解。
# 5. Lyndon Tree
- $\large\color{blue}\bf\circledast$ **定义** : $\rm Ly$ 的标准分解。
**定理(1.4)** 告诉我们，$\rm Ly$ 总是由两个更小的 $\rm Ly$ 按字典序拼成的。
由此定义 $\rm Ly$ 串 $s$ 的标准分解为 $s=ab$ ，其中 $b$ 恰为 $s$ 的最小严格后缀。
由 **定理(1.4)** 的证明可知，$a,b$ 均为 $\rm Ly$ 串，且 $a<b$ 。
- $\large\color{blue}\bf\circledast$ **定义** : $\text{Lyndon Tree}$
$\text{Lyndon Tree}$ 是一棵有根二叉树，每个节点代表一个 $\rm Ly$ 串。
根节点对应原串 $s$ ，要求 $s$ 是一个 $\rm Ly$ 串。
某个节点 $t$ 的两个儿子恰为 $t$ 的标准划分 $t=ab$ 中的 $a,b$。
若不能划分（只剩一个字符）则为叶子。
将 $s$ 在 $<_f$ 下的 $\text{Lyndon Tree}$ 记为 ${\rm LyTree}_f(s)$。
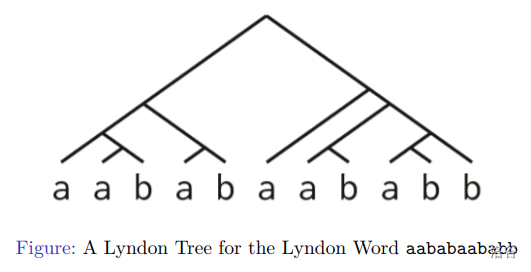
（阅读上图的正确姿势 ： 将子树内的所有字符顺次连接，即得到该节点代表的串）
一个显然的事实是，节点 $u=[l,r]$ 的子树中恰有叶节点 $l...r$。
实际上这玩意本质上是 $\rm SA$ 的 $\rm rank$ 数组的笛卡尔树。构造方法和前文计算 ${\rm Ly}_{s}(i)$ 的方法相同。
对于非 $\rm Ly$ 串，定义其 $\text{LyTree}$ 为其 $\rm Ly$ 分解中各个串的 $\rm LyTree$ 组成的森林。
- $\color{blue}\bf\Delta$ **定理(5.1)** 记 ${\rm lca}([l,r])$ 为**叶**节点 $l...r$ 在 $\rm LyTree$ 上的 $\rm lca$。
若 $s$ 的子串 $s[l,r]$ 是 $\rm Ly$ ，则 $u={\rm lca}([l,r])=[l_u,r_u]$ ，满足 $l=l_u\leq r\leq r_u$。
$l=r$ 时显然成立，考虑 $l<r$。
令 $v_0=[l_u,m_u],v_1=[m_u+1,r_u]$ 分别为 $u$ 的左右儿子。
由 $\rm LCA$ ，不难发现 $l_u\leq l\leq m_u<m_u+1\leq r\leq r_u$。
由此，可以将 $s[l_u,m_u],s[l,r],s[m_u+1,r_u]$ 分别写成 $ca,ab,bd$ 的形式。（$a,b$ 非空，$c,d$ 可空）
且 $(ca,bd)$ 是 $s[l_u,r_u]=cabd$ 的标准分解。
由 $s[l,r]=ab$ 是 $\rm Ly$ ，可得 $ab<b\Rightarrow abd<bd$ 。
若 $c$ 非空，则最小严格后缀可以是 $abd$ 而不可能是 $bd$ ，与标准分解的定义矛盾。因此 $c$ 必为空串，即 $l_u=l$。
- $\color{blue}\bf\Delta$ **定理(5.2)** 从任一个 $l$ 开始的最长 $\rm Ly$ 子串 $s[l,r]$ 必然在 $s$ 的 $\rm LyTree$ 中。
利用 **定理(5.1)** ，求 $u={\rm lca}([l,r])=[l,r']\ (r'\geq r)$。
又因为 $s[l,r]$ 是最长的，所以只能是 $r'=r$ ，故树中的 $u$ 即为 $s[l,r]$ 。
- $\color{blue}\bf\Delta$ **定理(5.3)** $s[l,r]$ 是 $l\ (l>1)$ 开始的最长 $\rm Ly$ 串 $\Leftrightarrow$ 节点 $u={\rm lca}([l,r])$ 是一个右儿子。
充分性 ： 对于任意的 $r'>r$ ， $s[l,r']$ 都不是 $\rm Ly$ ，显然 $s[l,r]$ 不可能是另一个 $\rm Ly$ 的标准分解的左半部分。
再根据 **定理(5.2)** ，其一定在树上，则只能是右儿子。
必要性 ： 若 $s[l,r]$ 不是 $l$ 开始的最长 $\rm Ly$ ，则存在 ${\rm Ly}\ s[l,r']$ 满足 $r'>r$。
根据 **定理(5.1)** 可得存在 $r''\geq r'>r$ 满足 ${\rm lca}([l,r'])=s[l,r'']$ ，且显然为 $s[l,r]$ 的祖先。
所以，$s[l,r]$ 显然不可能为右儿子。（只能从 $s[l,r'']$ 一串左链下来）
**推论** ： 结合 **定理(3.4)** ，对于任意一个 ${\rm run}\ {\bf r}$ ，若其正序为 $f$ ，其所有 $\rm LyRoot$ 都在 ${\rm LyTree}_f(s)$ 的右儿子中出现。
- **引理(5.1)** $\text{Weak Periodicity Lemma}$ : 若 $p,q$ 为 $s$ 的周期，且 $p+q\leq |s|$ ,则 $\gcd(p,q)$ 也是 $s$ 的周期。
证明见 [Border理论小记](https://www.luogu.com.cn/blog/command-block/border-li-lun-xiao-ji)。该引理简称为 $\rm WPL$。
- **子串半周期查询**
**题意** : 支持快速查询母串 $s$ 的某个子串是否有不超过长度一半的周期，如果有则求出最小周期。
记 ${\rm exrun}(l,r)$ 为满足 $l'\leq l,r\leq r',p\leq (r-l+1)/2$ 的一个 ${\rm run}\ {\bf r}=(l',r',p)$。
也就是说，能覆盖 $[l,r]$ ，且循环节长度小于区间一半的 $\rm run$。
根据 $\rm WPL$ ，若 ${\rm exrun}(l,r)$ 存在则必然唯一，否则可以在 $[l,r]$ 中构造更小的循环节。
这可以视作 **定理(3.1)** 的扩展 : 两个 ${\rm run}\ {\bf r_1}=(l_1,r_1,p_1),\ {\bf r_2}=(l_2,r_2,p_2)\ (p_1≠p_2)$ ，的交 $<p_1+p_2$ ，否则可以在相交的部分构造出更小的循环节 $\gcd(p_1,p_2)$。
不难发现，子串半周期查询问题等价于求 ${\rm exrun}(l,r)$。
算法为 ： 构造 ${\rm LyTree}_0(s),{\rm LyTree}_1(s)$ ，分别找到 $a_0={\rm lca}_0\Big(\big[l,\lceil (l+r)/2\rceil\big]\Big),a_1={\rm lca}_1\Big(\big[l,\lceil (l+r)/2\rceil\big]\Big)$ ，检查其右儿子作为 $\rm LyRoot$ 对应的 $\rm run$ 是否满足条件。
正确性证明 ：
假设有 ${\bf r}={\rm exrun}(l,r)=(l',r',p)$ ，由于 $p\leq (r-l+1)/2$ 一定存在一个 ${\rm LyRoot}\ λ =[i_λ ,j_λ]$ 包含 $\lceil (l+r)/2\rceil$ 这个位置。
设 ${\bf }r$ 的正序为 $f$ ，根据 **定理(5.3)** ，$λ$ 在 ${\rm LyTree}_f(s)$ 中作为右儿子出现。
由 $a_f={\rm lca}_f\Big(\big[l,\lceil (l+r)/2\rceil\big]\Big)$ ，可得 $a_f$ 同样包含 $\lceil (l+r)/2\rceil$ 这个位置。且 $a_f$ 的长度 $\geq\big[l,\lceil (l+r)/2\rceil\big]$ 的长度 $>p$。
综上不难推出 $a_f$ 是 $λ$ 的祖先。
若其右儿子 $b=[l_b,r_b]≠λ$ ，根据 $\rm LCA$ 的定义， $b$ 一定包含 $\lceil (l+r)/2\rceil$ 且不包含 $i$，则 $b$ 也是 $λ$ 的祖先。
由于 $λ$ 都是右儿子，可得 $i<l_b<i_λ$ 。
若 $r_b\leq r'$ ，则 $s[l_b,r_b]$ 有周期 $p$ ，与 $\rm Ly$ 矛盾。
若 $r_b>r'$ ，由正序的定义有 $s[r+1]<_fs[r+1-p]$ ，则可以发现 $s[l_λ,r_b]<_fs[l_b,r_b]$，同样与 $\rm Ly$ 矛盾。
综上，$λ$ 必为 $a_f$ 的右儿子。
# 6. 本原平方串（primitive square）
- $\large\color{blue}\bf\circledast$ **定义** : 若一个串 $s$ 的最小周期恰为 $|s|/2$ ，则称之为本原平方串，即 $\text{primitive square}$。
例 ： $\texttt{abcabc}$ 是本原平方串，而 $\texttt{abac,abababab}$ 则不是。
- **引理(6.1)** : 若 $a$ 为 $b$ 的前缀，且 $a$ 有 $p$ 的循环节，$b$ 有 $q$ 的循环节，$p|q,\ q\leq |a|$ ，则 $b$ 也有 $p$ 的循环节。
显然。
- **引理(6.2)** 若非空串 $s,t$ 满足 $ss$ 是 $tt$ 的前缀，且 $2|s|>t$ ，则 $|t|-|s|$ 是 $s$ 的周期。
画画图不难理解，这里略去严格证明。
- $\color{blue}\bf\Delta$ **定理(6.1)** ： 若非空串 $u,v,w$ 满足 $uu$ 是 $vv$ 的前缀，$vv$ 是 $ww$ 的前缀，且 $uu$ 是本原平方串，则有 $|u|+|v|\leq |w|$
> 证明比较长，建议大家记下导出的不等式和每个串已经导出的周期，而且不要把不同情况的讨论弄混了。
若 $|w|\geq 2|v|\geq |v|+|u|$ 则自然成立，所以只考虑 $|w|<2|v|$ 的情况。
由 **引理(6.2)** 可得，$|w|-|v|$ 是 $v$ 的周期。
假设 $|u|+|v|>|w|\Rightarrow |w|-|v|<|u|$，所以 $|w|-|v|$ 也是前缀 $u$ 的周期。
若 $2|u|\leq |v|$ ，则 $uu$ 是 $v$ 的前缀，可推知 $|w|-|v|$ 也是 $uu$ 的周期。此时，则有周期 $|w|-|v|<|u|=|uu|/2$ ，和本原平方串的定义矛盾。
若 $2|u|>|v|$，此时由 **引理(6.2)** 可得 $|v|-|u|$ 是 $u$ 的周期。
此外， $|u|,|w|-|v|$ 是 $v$ 的**不同**周期。但是，由于 $v$ 是本原平方串（长度超过一半的）的前缀，所以其是弱周期串（没有不超过长度一半的周期）。
若对一个串使用 $\rm WPL$ ，得到的循环节必然不超过长度一半（得到强周期串），所以可以否定其前提条件，即有 $|u|+|w|-|v|\not\leq |v|\Rightarrow |u|+|w|> 2|v|$。
令 $vs_1=w,u=s_1s_2,v=us_3=s_1s_2s_3$ ，则有 $w=s_1s_2s_3s_1$。
$|u|+|w|> 2|v|\Rightarrow |s_1s_2|+|s_1s_2s_3s_1|> 2|s_1s_2s_3|\Rightarrow |s_1|>|s_3|$
$|u|+|v|>|w|\Rightarrow |s_1s_2|+|s_1s_2s_3|> |s_1s_2s_3s_1|\Rightarrow |s_2|>0$ （保证代换有意义）
将 $uu,vv,ww$ 并排写出 ：
$$\begin{aligned}
&\boxed{\phantom{|||||||||}s_1\phantom{|||||||||}} \boxed{\phantom{|||}s_2\phantom{|||}} {\color{red}\boxed{\phantom{|||||||||}s_1\phantom{|||||||||}}} \boxed{\phantom{|||}s_2\phantom{|||}}\\
&\boxed{\phantom{|||||||||}s_1\phantom{|||||||||}} {\color{red}\boxed{\phantom{|||}s_2\phantom{|||}} \boxed{\phantom{||||||}s_3\phantom{||||||}}} \boxed{\phantom{|||||||||}s_1\phantom{|||||||||}} {\color{red}\boxed{\phantom{|||}s_2\phantom{|||}} \boxed{\phantom{||||||}s_3\phantom{||||||}}}\\
&\boxed{\phantom{|||||||||}s_1\phantom{|||||||||}} \boxed{\phantom{|||}s_2\phantom{|||}} \boxed{\phantom{||||||}s_3\phantom{||||||}} \boxed{\phantom{|||||||||}s_1\phantom{|||||||||}} {\color{red}\boxed{\phantom{|||||||||}s_1\phantom{|||||||||}}} \boxed{\phantom{|||}s_2\phantom{|||}} \boxed{\phantom{||||||}s_3\phantom{||||||}} \boxed{\phantom{|||||||||}s_1\phantom{|||||||||}}
\end{aligned}$$
由红色部分可以得出，$|s_2|$ 是 $s_2s_3$ 的周期。此外，$s_2s_3$ 是 $u=s_1s_2$ 的前缀，所以也有周期 $|v|-|u|=|s_3|$。
使用 $\rm WPL$ 可得 $s_2s_3$ 有周期 $r=\gcd(|s_2|,|s_3|)$。由 **引理(6.1)** 得 $u$ 也有周期 $r$。
接下来考虑 $u=s_1s_2$ ，其周期有 $|w|-|v|=|s_1|$ 和 $r$ ，而 $r\leq |s_2|$ ，所以继续使用 $\rm WPL$ 可得周期 $r'=\gcd(r,|s_1|)=\gcd(|s_1|,|s_2|,|s_3|)$。
这表明 $u$ 有非平凡整周期，和本原平方串的定义矛盾。证毕。
- **推论①** : 串 $s$ 中（位置不同的）本原平方串的个数不超过 $O(|s|\log |s|)$。
考虑每个开头位置，若有两个本原平方串 $uu,vv$ ，则下一个的长度至少为前两个的和（最劣为斐波那契），如此重复不超过 $O(\log n)$ 轮。
- **推论②** : 串 $s$ 中（本质不同的）本原平方串的个数不超过 $O(|s|)$。
考虑每个开头位置，若有三个本原平方串 $uu,vv,ww (|u|<|v|<|w|)$ ，则有 $|w|\geq |u|+|v|>2|u|$ ，所以 $uu$ 在每个 $w$ 中都出现了一次，并不是在此处第一次出现，暂不统计。
这样，每个开头位置出现的本质不同的本原平方串就至多两个。
听说本质不同的平方串也是 $O(|s|)$ 的。
- $\color{blue}\bf\Delta$ **定理(6.2)** ： 每个本原平方串一定属于恰好一个和它周期对应的 $\rm run$ 的一部分。
某个本原平方串 $uu$ 本身就足以成为一个周期为 $|u|$ 的 $\rm run$ ，还可能可以向两边扩展，所以这样的 $\rm run$ 一定存在。
由 **定理(3.1)** ，不会有两个周期对应的 $\rm run$ 包含同一个本原平方串。
- **找出本原平方串**
由 **定理(6.2)** ，只需要对每个 $\rm run$ 找出其中所有本原平方串即可。
由最小循环节的性质，在 ${\rm run}\ {\bf r}=(l,r,p)$ 中， $[l,r]$ 中任意连续长为 $2p$ 的子串都是本原平方串。
寻找的复杂度也可以写成 $\sum\limits_{{\bf r}=(l,r,p)\in{\rm Runs(s)}}r-l+2-2p$ ，可得该式为 $O(n\log n)$ 量级。
- $\color{green}\bf\Delta$ **例题**
- [P6629 [ZJOI2020] 字符串](https://www.luogu.com.cn/problem/P6629) | [Sol](https://www.luogu.com.cn/blog/command-block/solution-p6629)
- [Uoj#429. 【集训队作业2018】串串划分](https://uoj.ac/problem/429) | [Sol](https://www.luogu.com.cn/blog/command-block/str-ji-lu-uoj429-ji-xun-dui-zuo-ye-2018-chuan-chuan-hua-fen)