细说虚功原理

· · 个人记录

文章导航

认真讲一下。

需要简单的微积分和基础的力学知识。

向量用黑体表示。为了方便，我们会用牛顿上面加点的方式表示对时间的导数。

0. 基本概念

我们考虑一个质点系（系统）。系统内所有质点位置的集合称为位形。

然后系统要受到一些约束来限制位形的变化，比如物块放到平面上不能掉下去，平面限制了小物块位置的变化。

一般来说，约束可以写成这样的形式：

f(\bold{r}_1,\cdots,\bold{r}_n,\dot{\bold{r}}_1,\cdots,\dot{\bold{r}}_n,t)=0

上面的式子比较抽象，这里作简单说明。

约束带来的力称为约束（反）力，比如物块放在水平面上，弹力是为了满足平面约束而必须有的，它是一种与违背约束相对抗的反作用力；而对应的重力称为主动力，它不是依赖于约束而存在的。

1. 虚位移，理想约束，虚功原理

仅仅有约束我们还不足以确定运动状态。比如将静止物块放在水平面上后，仅依靠约束，它有可能向各个方向运动（也可能静止）；然而实际上由动力学规律，它只可能静止。上面所谓 “可能” 的位移指的是符合约束的位移，我们称为虚位移，这是我们想象出来的，并非实际的运动（时间并没有变化）。对于定常约束，真实的位移就是虚位移中的一个（指的是 “看上去” 一模一样）。我们研究问题的步骤就是先确定符合约束的位移，然后再判定哪个虚位移是真实位移。在传统方法中，我们需要启动牛顿第二定律才能得到真实位移；但我们也可以使用另外的方法，通过一系列判定条件（比如下面的虚功原理）来确定真实位移，这就是分析力学的思想。

上面的文字只是一个较为粗略的对思路的描述，有必要做一些更深入的说明。

我们考察的都是无穷小的虚位移，用 \delta\bold{r} 表示。这里 \delta 是等时变分符号。变分符号与微分符号的区别是，微分的 \mathrm{d}\bold{r} 指的是，实际情况中，经过极小时间 \mathrm{d}t，位置矢量的变化量，即一个极小的实位移，同时伴随时间的增加；而变分指的是，对于原来这个状态进行微扰（或者认为单纯只是另外一个位形接近的状态）带来的变化（虚位移），此时时间并没有变化，即 \delta t=0（所以称为 “等时” 变分）。画一个图：

（为了更好表示，上面的图画的是标量 r，下面推导也写标量）

我们考察 (t,r) 处的点，我们会发现，对这个点先微分再变分与先变分再微分的结果是完全相同的。于是我们有：

r+\mathrm{d}r+\delta(r+\mathrm{d}r)=r+\delta r+\mathrm{d}(r+\delta r) $$\mathrm{d}(\delta r)=\delta(\mathrm{d}r)$$ 这被称为 $\delta$ 与 $\mathrm{d}$ 的可对易性：它们可以进行任意交换，运算规则也相同，它们只是因为表示意义不同而有不同的符号。 引入虚位移的一大好处是，大多数约束力做的虚功为零。这里“虚功”的意思是力和虚位移的点乘，并不是一种实际的功。约束力做的虚功为零的约束称为理想约束。 下面这些约束都是理想约束： 与光滑表面接触；光滑铰接；质点用张紧且不可伸长轻绳连接…… > 如果是静力平衡的情况那么上面这些都是显然的。这里说明一下，在非定常条件下质点光滑表面接触（光滑表面不属于系统）也是理想约束。 > > 我们设光滑表面带来的约束为 $f(x,y,z,t)=0$（光滑表面可以运动），那么虚位移应当满足： > > $$\dfrac{\partial f}{\partial x}\delta x+\dfrac{\partial f}{\partial y}\delta y+\dfrac{\partial f}{\partial z}\delta z=0$$ > > 如果使用 $\mathrm{d}$ 的话（也就是实际情况下），应当有 $\dfrac{\partial f}{\partial t}\mathrm{d} t$ 这一项，实际做的功并不为零。然而注意虚位移的定义，$\delta t=0$，虚位移是被限制在某一时刻的切向上的。 由理想约束下约束力不做功，我们记质点 $i$ 受到的主动力为 $\bold{F}_i$，约束力为 $\bold{N}_i$，作虚位移 $\delta\bold{r}_i$。在理想约束的条件下，有： $$\delta W=\sum\limits_{i=1}^{n}(\bold{F}_i+\bold{N}_i)\cdot\delta\bold{r}_i=\sum\limits_{i=1}^{n}\bold{F}_i\cdot\delta\bold{r}_i=0$$ 这就得到虚功原理： 具有理想约束的质点系达到平衡的充分必要条件是在任何虚位移上，主动力做的虚功的和为零。 （必要性证明不难） 这给了我们只需作出主动力就能做题的方法。试试看！ **例 1.1** 如图，现有线密度为 $\lambda$ 的均质链条，它静止悬挂时两端各受的力为 $T_1,T_2$，两端高度差为 $h$。证明 $T_2-T_1=\lambda gh$. 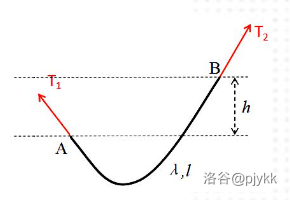![](https://cdn.luogu.com.cn/upload/image_hosting/efck99ze.png) 自然想到应当考虑沿原来绳子的方向的虚位移，但是首先有一个问题是，绳子的形状会变，然后什么都变了，算不了一点。 这里的技巧是，直接把条件改了，让绳子不是自由垂落，而是用一个和原来绳子形状相同的光滑管套在绳子外面。这样并不会改变各个力的大小，但是能使绳子只沿原方向，相当于减小了自由度。 此时仍然保证理想约束。由重力（保守力）做功的性质及虚功原理得 $$T_2\delta s-T_1\delta s-\lambda gh\delta s=0$$ 即得结论。 我们再来看一个流体的问题（帕斯卡定律）。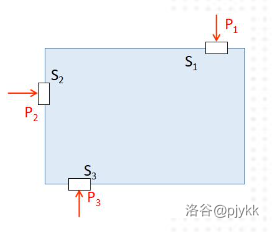 **例 1.2** 如图，容器内有不可压缩的流体且处于平衡状态，忽略活塞摩擦及重力，求证 $\dfrac{P_1}{S_1}=\dfrac{P_2}{S_2}=\dfrac{P_3}{S_3}$.（尊重原图，用 $P$ 表示力） ![](https://cdn.luogu.com.cn/upload/image_hosting/63a2kz9b.png) 考虑一个 $P_1$ 处向内压的虚位移 $\delta x_1$，此时 $P_2,P_3$ 处分别有向外虚位移 $\delta x_2,\delta x_3$，由体积不变及虚功原理： $$S_1\delta x_1-S_2\delta x_2-S_3\delta x_3=0\\P_1\delta x_1-P_2\delta x_2-P_3\delta x_3=0$$ 消去 $\delta x_1$ 得 $$\left(\dfrac{P_1S_2}{S_1}-P_2\right)\delta x_2+\left(\dfrac{P_1S_3}{S_1}-P_3\right)\delta x_3=0$$ 这时，关键在于 $\delta x_2$ 和 $\delta x_3$ 是独立的，因此我们只能让两个括号内式子都为 $0$，化简即得结论。 从这个例子可以看出，最后我们需要化为互相独立的虚位移的线性组合的形式，这就要求我们需要把不独立的虚位移消掉。 虚功原理能够大量减少约束力的分析。经典的例子是这个题： **例 1.3** 如图由四根长 $L$ 重 $mg$ 的杆和四根长 $2L$ 重 $2mg$ 的杆光滑铰接而成，杆间夹角均为直角。一根不可伸长的细绳连接两铰接点，求细绳的拉力 $T$。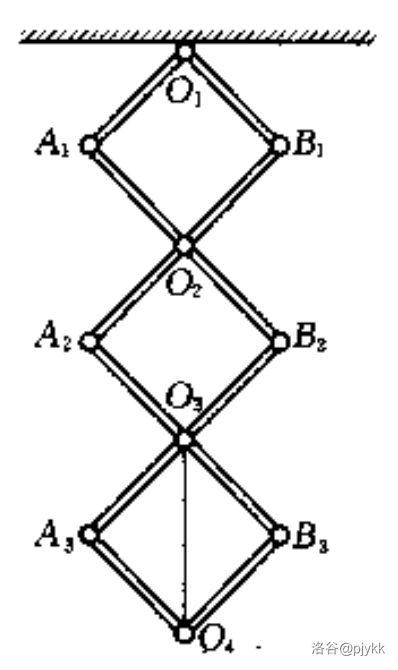 ![](https://cdn.luogu.com.cn/upload/image_hosting/8ey1ejh0.png) $T$ 是约束力，但也可以用虚功原理求。做法简单粗暴，就是直接解除约束，把绳子扬了，用两个主动力 $T$ 来替代。 设 $O_2$ 点有向下虚位移 $\delta x$，根据比例关系易得其它各点的虚位移，直接列式子： $$T\cdot 2\delta x-T\cdot 3\delta x+2\cdot mg\cdot\dfrac{1}{4}\delta x+2\cdot 2mg\cdot\delta x+2\cdot 2mg\cdot2\delta x+2\cdot mg\cdot\dfrac{11}{4}\delta x=0$$ 得 $T=18mg$，做完了。 但是来看这个平衡题： **例 1.4** 如图，质量为 $m$ 的均匀细杆与光滑表面相切，求平衡时杆与水平面的夹角 $\theta$ 与图中长度的关系。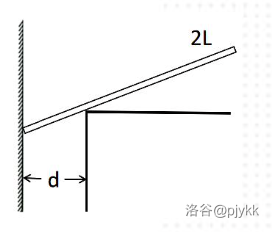 ![](https://cdn.luogu.com.cn/upload/image_hosting/ekuikse5.png) 按照之前虚位移的理论，我们考虑一个质心的虚位移 $\delta r$。只有重力为主动力，虚位移 $\delta r$ 仅有竖直方向的分量 $\delta y$ 对做功有贡献，于是 $$-mg\delta y=0$$ $m=0$ 疑似有点扯了，所以得到平衡位置 $\delta y=0$。 这里有一个问题，就是我们本来是希望是要做虚位移的，结果最后解出所设的“虚位移”根本不存在，这里所谓的虚位移是不符合定义的，只是在数学上满足这样的关系。 不过在这个题中我们可以用数学方法处理。 为了解出关系我们先用 $\theta$ 表示 $y$ （以水平面为高度零点）得 $$L\sin\theta-d\tan\theta=y$$ 同取 $\delta$ 得 $$L\cos\theta\delta\theta-\dfrac{d}{\cos^2\theta}\delta\theta=\delta y=0$$ 这下 $\delta\theta$ 总不可能为 $0$ 了，于是得到 $$\cos^3\theta=\dfrac{d}{L}$$ 我们能够明显感受到这道题与前面两道题的区别，直接用虚功原理遇到了困难。我们把一些问题总结在这里： * 首先 “虚位移” 本身就是一个比较抽象的概念。我们为消掉约束力引入了虚位移，但是虚位移这个东西又高度依赖约束，结果是找合适的虚位移反而成了困难的部分了。有时我们设了看似有的虚位移，结果最后实际上并不存在。并且我们不知道要怎么判断这种情况，只能推矛盾。 * 注意上面对于虚功原理的讨论是基于虚 “位移” 的，首先要有位移。但有时用位移来表示是相当复杂的，不如直接用一个 $\theta$。 * 虚位移的不独立。写出虚位移之后需要找出虚位移间关系进行消元。 解决这些问题的方案其实上面已经有了：不拘泥于 “位移”，也可以使用 $\theta$ 这样的东西来表示。这就引出了广义坐标。 ## 2. 广义坐标下的虚功原理 广义坐标指的是一组独立的参数 $q_1,\cdots,q_s$，用它们能够唯一确定系统位形。广义坐标的个数 $s$ 称为系统（有限运动中）的自由度。 举一个经典的例子，考虑一个单摆（摆角不超过 $90^{\circ}$）。 * 我们可以用单独的角度 $\theta$ 来表示位形，单独的 $\theta$ 是广义坐标。 * 单独的 $x$ 也是广义坐标，但是显然不如 $\theta$ 好。 * 单独的 $y$ 不是广义坐标，因为无法区分左右两状态。 * $(x,y)$ 不是广义坐标，因为两个参数不相互独立。 > “无法区分左右两状态” 这句话道出了 **例 1.4** 中出现 $\delta y=0$ 的根本原因。那个题的平衡状态就像是单摆的平衡状态（只是稳定性有差别）。 因为使用广义坐标就已经能唯一确定位形，我们无需再找出坐标间关系（不用管约束方程了）。 类比原有的运动学概念，广义坐标关于时间的导数称为广义速度。在我们目前讨论的问题（完整约束）中，广义速度、广义坐标的变分也是相互独立的。 接下来我们尝试将广义坐标代入到虚功原理的式子中。 设位矢 $\bold{r}_i=\bold{r}_i(q_1,\cdots,q_s,t)$，取变分有 $$\delta\bold{r}_i=\sum\limits_{\alpha=1}^s\dfrac{\partial\bold{r}_i}{\partial q_\alpha}\delta q_\alpha$$ 代入到虚功原理的式子中有 $$\begin{aligned}\delta W&=\sum\limits_{i=1}^{n}\bold{F}_i\cdot\delta\bold{r}_i\\&=\sum\limits_{i=1}^{n}\bold{F}_i\cdot\sum\limits_{\alpha=1}^s\dfrac{\partial\bold{r}_i}{\partial q_\alpha}\delta q_\alpha\\&=\sum\limits_{\alpha=1}^{s}\left(\sum\limits_{i=1}^n\bold{F}_i\cdot\dfrac{\partial\bold{r}_i}{\partial q_\alpha}\right)\delta q_\alpha\\&=0\end{aligned}$$ 与初始时的虚功原理作比较，我们可以定义广义力 $$Q_{\alpha}=\sum\limits_{i=1}^n\bold{F}_i\cdot\dfrac{\partial\bold{r}_i}{\partial q_\alpha}$$ 于是有 $$\delta W=\sum\limits_{\alpha=1}^sQ_{\alpha}\delta q_\alpha=0$$ 因为广义坐标的优秀性质（相互独立和唯一确定性），我们有 $$Q_{\alpha}=0$$ 我们可以看到，这个式子就不再包含原来的“虚位移”，是一个更加确定的形式。 实际上我们并不会对每个广义坐标求广义力，即直接用上面的式子进行运算，而是考虑每个主动力，计算它作的虚功。比如下面这道例题： **例 2.** 如图，杆 $OA,AB$ 长度分别为 $l_1,l_2$，各铰接处光滑，求 $\varphi_1,\varphi_2$。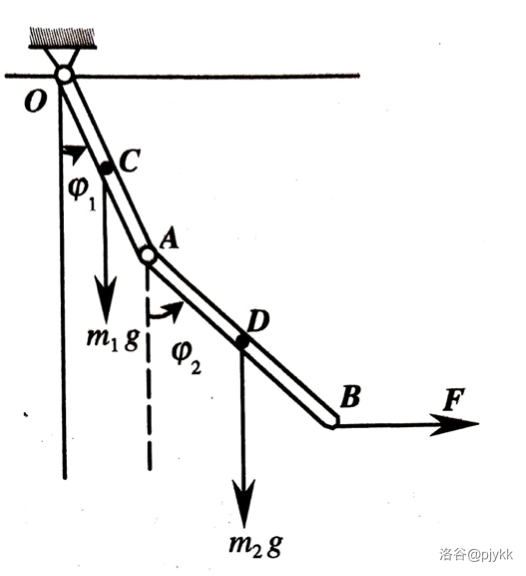 ![](https://cdn.luogu.com.cn/upload/image_hosting/8s2avnwa.png) 容易判定符合使用虚功原理的条件。我们取广义坐标 $\varphi_1,\varphi_2$，并以水平向右为 $x$ 轴正方向，以水平向下为 $y$ 轴正方向。 要算做功，只需表示 $y_C,y_D,x_B$，具体地，有： $$y_C=\dfrac{1}{2}l_1\cos\varphi_1\\y_D=l_1\cos\varphi_1+\dfrac{1}{2}l_2\cos\varphi_2\\x_B=l_1\sin\varphi_1+l_2\sin\varphi_2$$ 取变分，有 $$\delta y_C=-\dfrac{1}{2}l_1\sin\varphi_1\delta\varphi_1\\\delta y_D=-l_1\sin\varphi_1\delta\varphi_1-\dfrac{1}{2}l_2\sin\varphi_2\delta\varphi_2\\\delta x_B=l_1\cos\varphi_1\delta\varphi_1+l_2\cos\varphi_2\delta\varphi_2$$ 由虚功原理， $$m_1g\delta y_C+m_2g\delta y_D+F\delta x_B=0$$ 代入化简得 $$(Fl_1\cos\varphi_1-\dfrac{1}{2}m_1gl_1\sin\varphi_1-m_2gl_1\sin\varphi_1)\delta\varphi_1+(Fl_2\cos\varphi_2-\dfrac{1}{2}m_2gl_2\sin\varphi_2)\delta\varphi_2=0$$ 于是有 $$\begin{cases}Fl_1\cos\varphi_1-\dfrac{1}{2}m_1gl_1\sin\varphi_1-m_2gl_1\sin\varphi_1=0\\\\Fl_2\cos\varphi_2-\dfrac{1}{2}m_2gl_2\sin\varphi_2=0\end{cases}$$ 解得 $$\begin{cases}\varphi_1=\arctan\left(\dfrac{2F}{(m_1+2m_2)g}\right)\\\\\varphi_2=\arctan\left(\dfrac{2F}{m_2g}\right)\end{cases}$$ 练习：用类似的方法完成 **例1.4** 总结一下，我们做题的步骤是这样的： 1. 判定约束为双面、定常、几何、理想的约束。如果要求约束力，需要解除约束，用主动力替换（**例 1.3**）。 2. 判断自由度，选取合适的广义坐标。 3. 将每个主动力的作用点的位置用广义坐标表示。 4. 作变分，求出虚功。 5. 按广义坐标合并同类项，令各项为零，解方程组即得。 ## 3. 保守系统下的虚功原理与平衡的稳定性 很多主动力，比如恒力（重力可看作一种恒力），引力，库仑力，弹簧弹力等都属于保守力，有势能相对应。因此对于保守系统，我们可以使用势能来表示稳定条件。下面我们具体推导一下。 设势能函数为 $V$，由势能定理有 $$\delta V=-\delta W=-\sum\limits_{\alpha=1}^sQ_{\alpha}\delta q_\alpha$$ 由对易性 $\delta$ 可理解为 $\mathrm{d}$，我们立刻得到 $$Q_\alpha=-\dfrac{\partial V}{\partial q_\alpha}$$ 由 $Q_\alpha=0$，我们最终得到 $$\dfrac{\partial V}{\partial q_\alpha}=0$$ 上面的式子意义明显，就是说物体的平衡位置就是势能取驻值的位置。 实际上对于 **例 1.4**，我们最后的做法中 $\delta y=0$ 就相当于（重力）势能取极值。 然而并不是所有的平衡位置都是我们在日常生活中能够见到的。比如考虑一个半球面，我们将一个小球放到上面，它几乎必然会滑下；或者说，即使恰好将它放在了正上方，给一个任意小的微扰，它都会远离平衡位置滑下。我们称这种平衡为不稳定平衡。反过来，如果是半球碗内的球，那么即使给定一个微扰，它也会回复到原来的位置，这种平衡称为稳定平衡。另外我们还有随遇平衡的概念，指的是经过微扰后，物体停留在微扰后的位置，既不远离平衡位置，也不回复到平衡位置。 值得注意的是，引入势能函数，我们可以比较方便地得到平衡的稳定性。我们可以粗略认为，极值点的种类对应着稳定性的种类。简单来说，稳定平衡一般对应着势能函数的极小值，而不稳定平衡一般对应着势能函数在平衡位置不取严格极小值。随遇平衡则意味着势能函数在对应位置周围非无穷小的部分为定值。（这里的说法都不是很严谨；平衡稳定性的证明过于复杂，这里直观理解即可） 对仅一个广义坐标的情况（一元势函数），我们可以简单地对其进一步求导，判断二阶导数的符号即可。 > 若仅有重力势能，此时就是受力分析中所谓“重心升降法”的原理。 **例 3.1** 试判断 **例 1.4** 中平衡的稳定性。 重力势能只与纵坐标有关，只写纵坐标即可。我们沿用先前的符号， $$\begin{aligned}y&=L\sin\theta-d\tan\theta\\\dfrac{\mathrm{d}y}{\mathrm{d}\theta}&=L\cos\theta-\dfrac{d}{\cos^2\theta}\\\dfrac{\mathrm{d}^2y}{\mathrm{d}\theta^2}&=-L\sin\theta-\dfrac{2d\sin\theta}{\cos^3\theta}<0\end{aligned}$$ 因此为不稳定平衡。 **例 3.2** 如图，匀质杆 $AB$ 长度为 $l$，各接触面光滑。若杆在 $Oxy$ 平面上任意位形都为平衡位置，求柱面方程。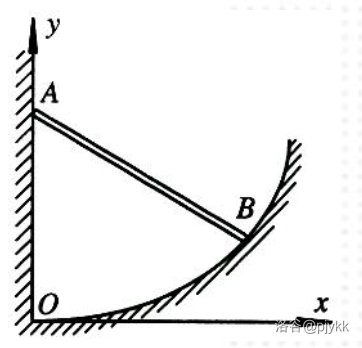 ![](https://cdn.luogu.com.cn/upload/image_hosting/z60dr83h.png) 随遇平衡意味着势能为常数，杆的重心高度不变。考虑竖直放置，此时重心高度为 $\dfrac{l}{2}$。设 $B(x,y)$，容易得到 $$\left(\dfrac{l}{2}-y\right)^2+\left(\dfrac{x}{2}\right)^2=\left(\dfrac{l}{2}\right)^2$$ 这就得到柱面方程。柱面在 $Oxy$ 平面上的截面为椭圆（的一部分）。 下面两个例子相对复杂一点。 **例 3.3** 如图，大圆环光滑，$A$ 为光滑小环，其上系两段绳子。$B$ 为光滑定滑轮，大小不计，两物体 $C,D$ 重力分别为 $P,G$，$D$ 与大圆环间无弹力。求平衡时的 $\varphi$ 及平衡稳定性。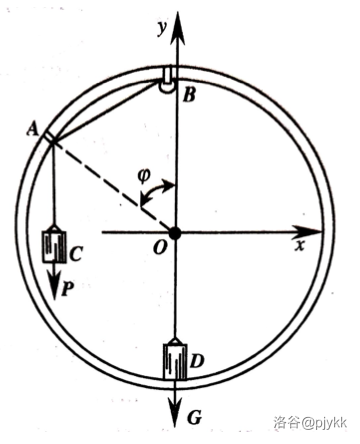 ![](https://cdn.luogu.com.cn/upload/image_hosting/7jdsce6c.png) 设 $CA$，$ABD$ 段绳长分别为 $l,L$，半径为 $R$，直接写重力势能 $$V=P(R\cos\varphi-l)+G(R-L+2R\sin\dfrac{\varphi}{2})$$ 求导 $$\dfrac{\mathrm{d}V}{\mathrm{d}\varphi}=-PR\sin\varphi+GR\cos\dfrac{\varphi}{2}=0$$ 解得 $\varphi_1=\arcsin\dfrac{G}{2P}$，注意有可能不存在。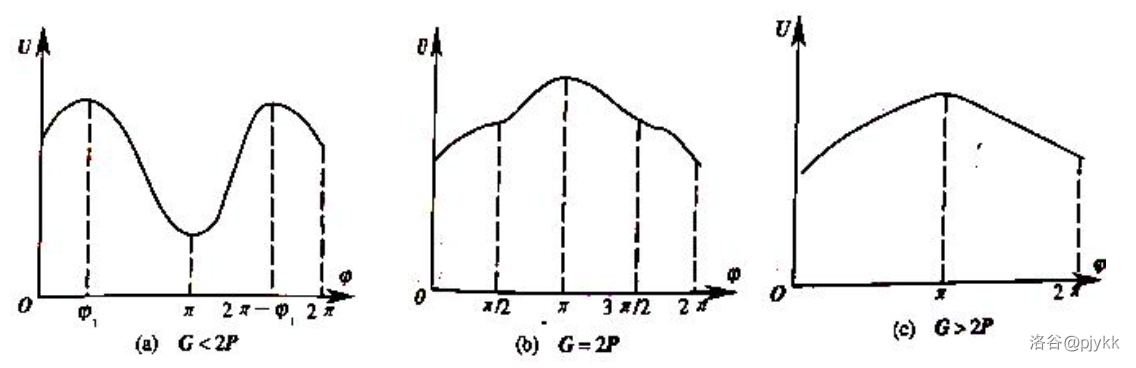 这里对于势能函数的讨论比较复杂，略去，直接给出最后的势能曲线： ![](https://cdn.luogu.com.cn/upload/image_hosting/pf5zptdx.png) **例 3.4** 如图，光滑圆环半径为 $R$，以 $\omega$ 角速度匀速转动。一根长 $L=\sqrt{2}R$ 的细杆放于环上，杆中心与圆心的连线与竖直方向夹角为 $\theta$。求平衡时 $\theta$ 大小，并讨论平衡稳定性。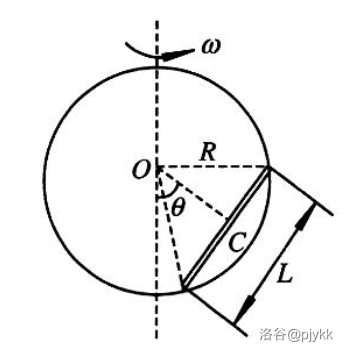 ![](https://cdn.luogu.com.cn/upload/image_hosting/epbpt2v0.png) 显然考虑换系，此时多出一项惯性离心力 $F^{*}=m\omega^2r$。 注意惯性离心力的大小只与到圆心的距离有关，我们可以引入离心势能。先算做功（注意力的方向向外） $$W^*=\int_{r_1}^{r_2}m\omega^2r\mathrm{d}r=\dfrac{1}{2}m\omega^2r_2^2-\dfrac{1}{2}m\omega^2r_1^2$$ 由 $\Delta V^*=-W^*$ 对比得 $$V^*=-\dfrac{1}{2}m\omega^2r^2$$ 考虑整根杆，由长度关系注意到杆所对圆心角为 $90^\circ$，设线密度 $\lambda=\dfrac{m}{\sqrt{2} R}$，有总离心势能 $$\begin{aligned}V^*&=-\dfrac{1}{2}\omega^2\int_{0}^{\sqrt{2}R}(R\sin(\theta-45^\circ)+x\cos\theta)^2\lambda\mathrm{d}x\\&=-\left(\dfrac{1}{4}-\dfrac{1}{6}\cos^2\theta\right)m\omega^2R^2\end{aligned}$$ 以 $O$ 为零势能点，又有重力势能 $V_G=-\dfrac{\sqrt{2}}{2}mgR\cos\theta

因此杆总势能

V=V_{G}+V^*=-\dfrac{\sqrt{2}}{2}mgR\cos\theta-\left(\dfrac{1}{4}-\dfrac{1}{6}\cos^2\theta\right)m\omega^2R^2

注意到这是关于 \cos\theta 的二次方程，有

V=\dfrac{1}{6}m\omega^2R^2\left(\cos\theta-\dfrac{3\sqrt{2}g}{2\omega^2R}\right)^2-\dfrac{1}{4}m\omega^2R^2-\dfrac{3mg^2}{4\omega^2}

当 \cos\theta=\dfrac{3\sqrt{2}g}{2\omega^2R} （若存在）时，V 取最小值，为稳定平衡。

再考虑 $\theta=0$，可以算出： * 当 $\dfrac{3\sqrt{2}g}{2\omega^2R}\geq1$ 时，为稳定平衡； * 当 $\dfrac{3\sqrt{2}g}{2\omega^2R}<1$ 时，为不稳定平衡。 ## 4. 后面是什么？ 简单介绍一点动力学问题的处理方案，基本上就是列举结论。 对于动力学问题，我们有时也会将它转化为静力学问题来进行解决。方法就是引入我们常说的“惯性力”。 我们记质点 $i$ 质量为 $m_i$，受到的主动力为 $\bold{F}_i$，约束力为 $\bold{N}_i$，位移为 $\bold{r}_i$，我们可以列出方程： $$\bold{F}_i+\bold{N}_i=m_i\ddot{\bold{r}}_i$$ 此时我们将右边一项移到左边： $$\bold{F}_i+\bold{N}_i-m_i\ddot{\bold{r}}_i=0$$ 将 $-m_i\ddot{\bold{r}}_i$ 这一项看作惯性力。在理想约束条件下，有 $$\delta W=\sum\limits_{i=1}^n(\bold{F}_i-m_i\ddot{\bold{r}}_i)\delta\bold{r}_i=0$$ 此式称达朗贝尔原理，也叫做动力学普遍方程。 接下来我们将广义坐标代入，设位矢 $\bold{r}_i=\bold{r}_i(q_1,\cdots,q_s,t)$，与之前相似，得到 $$\delta W=\sum\limits_{\alpha=1}^s\left(Q_{\alpha}-\sum\limits_{i=1}^n m_i\ddot{\bold{r}}_i\dfrac{\partial\bold{r}_i}{\partial q_\alpha}\right)\delta q_\alpha$$ 这可以使用一些技巧化简得到（不细推了） $$\delta W=\sum\limits_{\alpha=1}^s\left(Q_{\alpha}-\dfrac{\mathrm{d}}{\mathrm{d}t}\dfrac{\partial T}{\partial \dot{q_\alpha}}+\dfrac{\partial T}{\partial q_\alpha}\right)\delta q_\alpha=0$$ 其中 $T$ 为系统动能，即满足 $$T=\sum\limits_{i=1}^n\dfrac{1}{2}m_i|\dot{\bold{r}}_i|^2$$ 最终得到拉格朗日方程 $$\dfrac{\mathrm{d}}{\mathrm{d}t}\dfrac{\partial T}{\partial \dot{q_\alpha}}-\dfrac{\partial T}{\partial q_\alpha}=Q_{\alpha}$$ 当为保守力系时代入 $Q_\alpha$ 可得结论 $$\dfrac{\mathrm{d}}{\mathrm{d}t}\dfrac{\partial L}{\partial \dot{q_\alpha}}-\dfrac{\partial L}{\partial q_\alpha}=0$$ 其中 $L$ 为拉格朗日量，满足 $$L=T-V$$ 一个方程就把（完整系下的）动力学写明白了，非常厉害。