【图论】Tarjan 入门
_Weslie_
·
·
算法·理论
update 2025.8.21:发现几个锅,改一改。
这篇文章是题单 【图论】Tarjan 入门 的配套文章。
注意到 Tarjan 是一个算法,而不是一类问题。事实上有向图用 Tarjan 解决的问题和无向图用 Tarjan 解决的问题是两类不同的问题。我一般称之为“强连通分量问题”和“双连通分量问题”。
有向图的 Tarjan(强连通分量问题)
相比双连通分量问题,强连通分量问题应用更广泛一些。
强连通分量的定义
有向图 G 强连通是指,G 中任意两个结点连通。
例如下面的图就是强连通的:
强连通分量(Strongly Connected Components,SCC)的定义是:极大的强连通子图。
例如:
这张图中,\{7,8,9\} 构成一个强连通分量。另外的两个强连通分量分别是 \{2\} 和 \{1,3,4,5,6\}。虽然 \{1,3,4,5\} 两两之间也可达,但它不是最大的。
我们要运用到 Tarjan 算法。在 OI 中,Tarjan 算法一般是指求强连通分量或双连通分量的算法。
有向图的 dfs 树
这是一个有向图。
我们 dfs 遍历整张图。所经过的边应该是红色的边:
这些红边组成了一颗 dfs 树,这些边统称为树边。
但是还有一些边没有遍历到。
所以我们再定义两类边:
返祖边:顾名思义,从一个点连向其祖先的边叫做返祖边。
这张图中,蓝色的边是返租边:
但还有一些边没有被覆盖到。这些边我们叫做横叉边(下图中的紫色边)。
看图理解:横叉边就是在两个不同的子树里面乱插的边。
辅助数组:dfn 和 low
我们定义两个辅助数组和一个辅助栈。
注意:有向图和无向图中 low 的定义不同。
强连通分量的求解
文字描述
我们先来文字版叙述一遍过程:
- 当前节点 u 入栈,初始化 dfn_u 和 low_u(low_u\leftarrow dfn_u),标记节点入栈
-
遍历 u 的邻居 v。
- 如果 v 还没有被遍历过,那么 v 就是 dfs 树中 u 的儿子。遍历一遍,然后根据定义,令 low_u\leftarrow \min(low_u,low_v)。
- 否则,考虑 v 是否还在栈中。如果还在,则 low_u\leftarrow \min(low_u,dfn_v)。
- 遍历完邻居后,如果 low_u=dfn_u,说明子树内无法回到 u 以上的点,就将 u 还在栈中的子树分离出来成为一个新的强连通分量(注意标记该节点已不在栈中)。所以用栈——因为子树后遍历先出去,符合栈的特点。
图解
举个例子(点左边蓝色的权值为 dfn,右边红色的权值为 low):
先遍历前四个点,这都不在话下。这四个点依次入栈。
到 8 的时候,你会发现返租边所连的 1 还在栈中,所以 low_8=1。
向上更新 4 和 3 的 low。这都不在话下。
遍历 9,9 号点再遍历横叉边,得到 low_9=4。
向上回溯到 1,更新 low。这都不在话下。
然后遍历 7。7 连着一条到 5 的横叉边,于是 low_7=2。
继续往下遍历。(实际上 2 是 6 的祖先,但是这里没画好)
现在 low_6=8。向上回溯时发现,low_2=dfn_2(也就是说 2 的子树只能被困在 2 以下了。
于是把 \{2,6,10\} 三个点分出来,变成一个新的强连通分量(出栈)。
最后,把还在栈里面的点合成一个强连通分量。原因是 $low_1=dfn_1$。
得出结果:$\{2,6,10\}$ 和 $\{1,3,4,5,7,8,9\}$ 共两个强连通分量。
#### 代码实现
按照上面所说模拟即可。
```
//ins 指点是否在栈中
void dfs(int now){
dfn[now]=++idx;
low[now]=idx;
ins[now]=true;
st.push(now);
for(int i=head[now];i;i=e[i].nxt){
int v=e[i].v;
if(!dfn[v]){
dfs(v);
low[now]=min(low[now],low[v]);
}
else if(ins[v])low[now]=min(low[now],dfn[v]);
}
if(dfn[now]==low[now]){
++tot;
while(1){
int v=st.top();
st.pop();
g[tot].push_back(v);
ins[v]=false;
bel[v]=tot;
if(v==now)break;
}
}
}
```
#### 题目练习
- [B3609 [图论与代数结构 701] 强连通分量](https://www.luogu.com.cn/problem/B3609)
- [P2863 [USACO06JAN] The Cow Prom S](https://www.luogu.com.cn/problem/P2863)
- [P1726 上白泽慧音](https://www.luogu.com.cn/problem/P1726)
- [P1407 [国家集训队] 稳定婚姻](https://www.luogu.com.cn/problem/P1407)
这些题目全部在题单中有收录。
### 缩点及 dp
缩点就是把在同一强连通分量中的点当成一个点来看待。
缩完点之后的图是一个 DAG。原因是:假如还有环,那么这个环上的点就是一个新的强连通分量。
给一些例题(例题全部在题单中有收录):
- [P3387 【模板】缩点](https://www.luogu.com.cn/problem/P3387)
- [P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G](https://www.luogu.com.cn/problem/P2341)
- [SP14887 GOODA - Good Travels](https://www.luogu.com.cn/problem/SP14887)
- [P3627 [APIO2009] 抢掠计划](https://www.luogu.com.cn/problem/P3627)
- [P1073 [NOIP 2009 提高组] 最优贸易](https://www.luogu.com.cn/problem/P1073)
- [P2515 [HAOI2010] 软件安装](https://www.luogu.com.cn/problem/P2515)
- [P2272 [ZJOI2007] 最大半连通子图](https://www.luogu.com.cn/problem/P2272)
## 无向图的 Tarjan(双连通分量问题)
### 双连通分量、割点、割边的定义
对于一个无向图,如果把一个点删除后这个图的极大连通分量数增加了,那么这个点就是这个图的**割点**(又称割顶)。
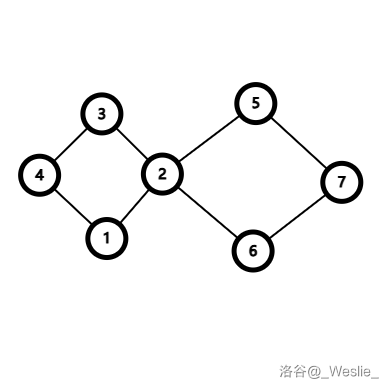
例如在上面这个图中,点 $2$ 就是一个割点。
如果删掉一条边后图中的连通分量数增加了,则称这条边为桥或者**割边**。
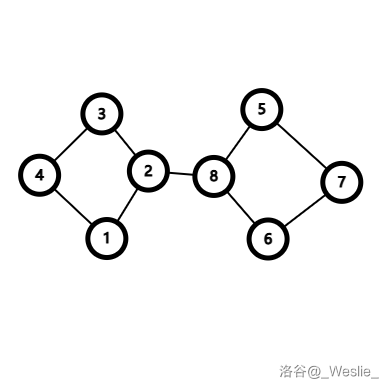
例如在上面这个图中,边 $(2,8)$ 就是一条割边。
对于无向图中的点对 $(u,v)$,若 $(u,v)$ 之间去掉任何一个点(不包括 $u$ 和 $v$ 自己)都无法使得它们不连通,那他们是**点双连通**的。换句话说,$(u,v)$ 之间至少存在两条路径(设它们经过的点的集合分别为 $A$ 和 $B$,其中 $A$ 和 $B$ 均不包含 $u$ 和 $v$),使得 $A\cap B=\varnothing$。也就是说,存在两条 $(u,v)$ 之间的路径除了起终点一样之外,中间不共同经过任何一个点。注意:“换句话说”后面的话**并不严谨**(仅仅是为了方便理解“双”的含义),因为它并未考虑到一张图只有 $(u,v)$ 一条边的情况,你会发现按照定义它们依然是点双连通的。
对于无向图中的点对 $(u,v)$,若 $(u,v)$ 之间去掉任何一条边都无法使得它们不连通,那他们是**边双连通**的。换句话说,$(u,v)$ 之间至少存在两条路径(设它们经过的边的集合分别为 $A$ 和 $B$),使得 $A\cap B=\varnothing$。也就是说,存在两条 $(u,v)$ 之间的路径中间不共同经过任何一条边。
在一个无向图 $G$ 中,一个**点双连通分量** $A$ 应满足:
- $A$ 是**极大的**。换句话说,不存在 $u\in G$ 且 $u\notin A$ 使得 $A\cup\{u\}$ 依然是一个点双连通分量。
- $\forall u,v\in A$ 且 $u\ne v$,$u$ 和 $v$ 是**点双连通**的。换句话说,在一个点双连通分量中随便抓两个不同的点,它们是点双连通的。
在一个无向图 $G$ 中,一个**边双连通分量** $A$ 应满足:
- $A$ 是**极大的**。换句话说,不存在 $u\in G$ 且 $u\notin A$ 使得 $A\cup\{u\}$ 依然是一个边双连通分量。
- $\forall u,v\in A$ 且 $u\ne v$,$u$ 和 $v$ 是**边双连通**的。换句话说,在一个点双连通分量中随便抓两个不同的点,它们是边双连通的。
### 无向图的 dfs 树
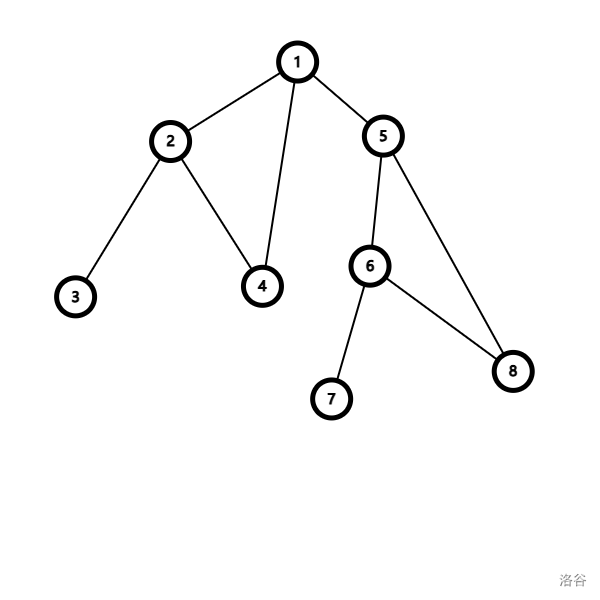
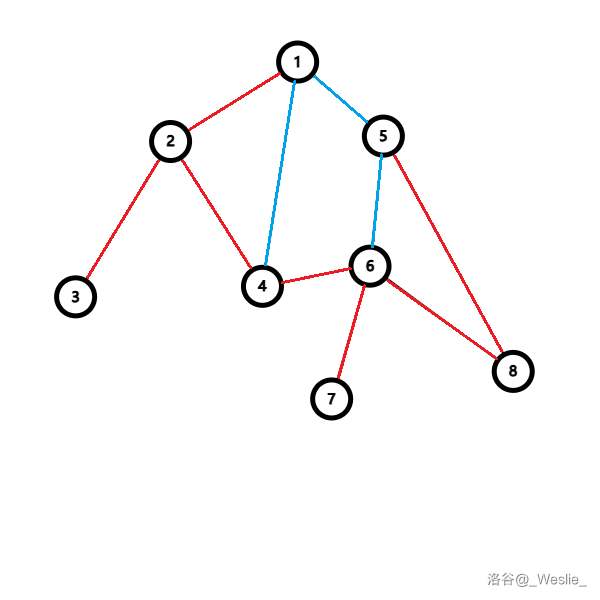
这是一张无向图。

红色的边是 dfs 树上的边,而蓝色的边是返祖边。
什么?你说,为什么没有横叉边?
因为如果存在一条紫色的横叉边:
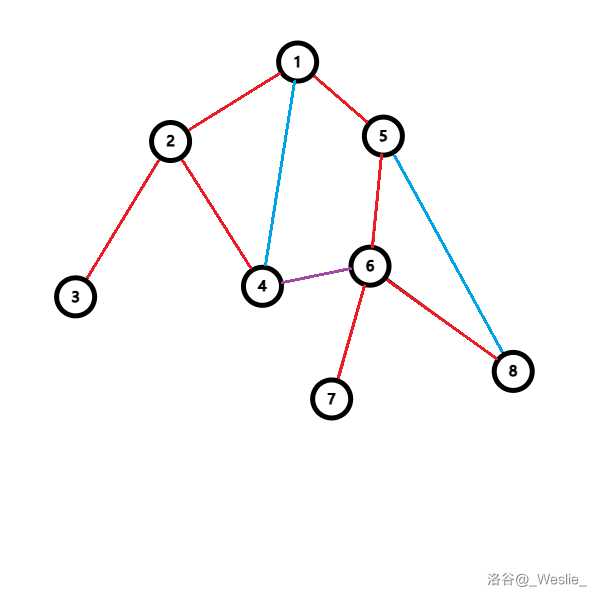
那么这张图在 dfs 到 $4$ 的时候,就会直接 dfs 到 $6$,这条紫色边就变成树边了。
### 无向图中 low 的定义
注意到前文中,我说过:有向图和无向图中 $low$ 的定义不同。
事实上,无向图中,$low$ 的定义是:$low_u$ 是节点 $u$ 在 dfn 树中,自身或后代能通过树边和返祖边触及到的 $dfn$ 值的最小值。
### 割边和边双连通分量的求法
#### 文字说明
边双连通分量相对简单的原因是:一个点不会出现在多个边双连通分量中。
我们简单描述一下用 Tarjan 算法解决割边和边双连通分量问题的过程:
1. 初始化,同有向图。
2. 枚举 $u$ 的邻居 $v$。
- 显然对 $u$ 的儿子 $v$ 有 $low_u\leftarrow\min(low_u,low_v)$。
- 如果 $v$ 是 $u$ 的邻居但不是 $u$ 的儿子且不是 $u$ 的父亲,那么 $(u,v)$ 就是返祖边。根据定义,$low_u\leftarrow\min(low_u,dfn_v)$。
3. 如果发现 $low_u=dfn_u$,那么连接 $u$ 和其祖先的边就是割边,$u$ 及其还在栈中的子树就构成一个边双连通分量。
#### 图解
举个例子(点左侧的红色数字为 $dfn$,右侧的蓝色数字为 $low$):

首先遍历 $1,2,3$,求 dfs 序。
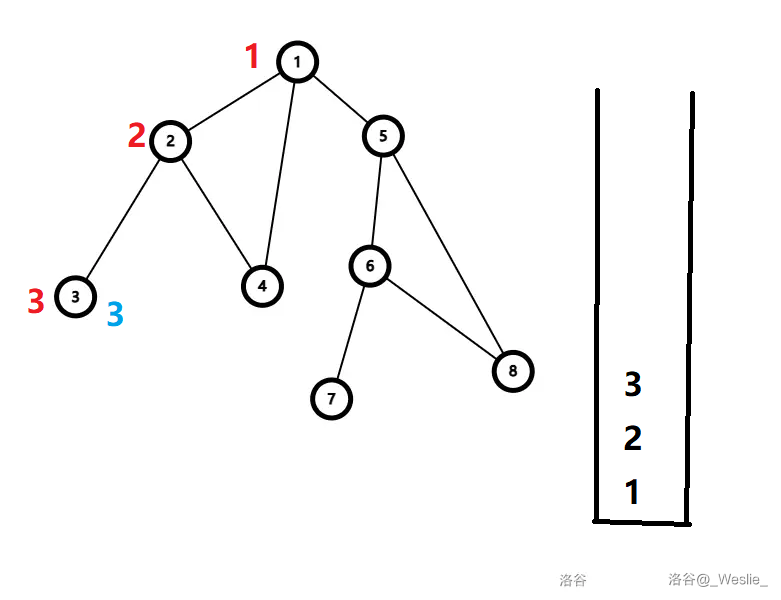
到 $3$ 时,发现 $low_3=dfn_3$,于是 $3$ 与其祖先的这一条边就是割边,$3$ 自己就是一个边双连通分量。
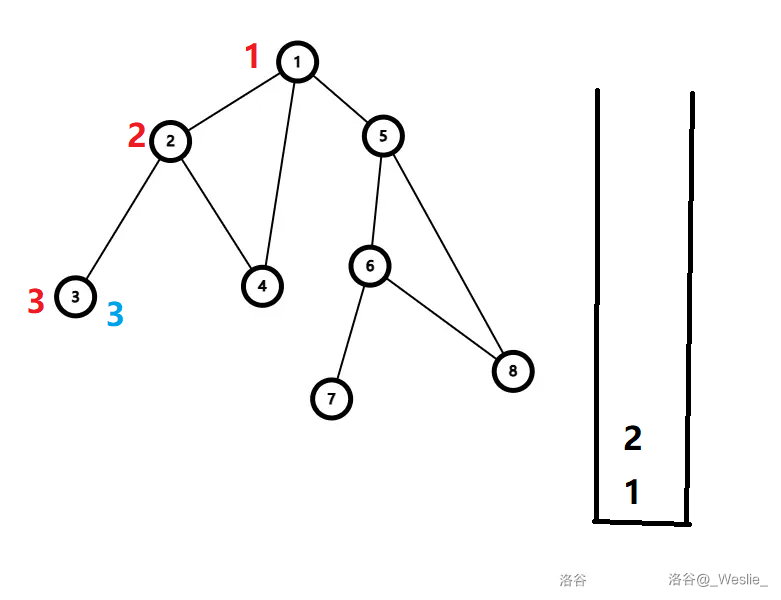
然后回溯到 $2$,再 dfs 到 $4$,记录 $low_4=1$。
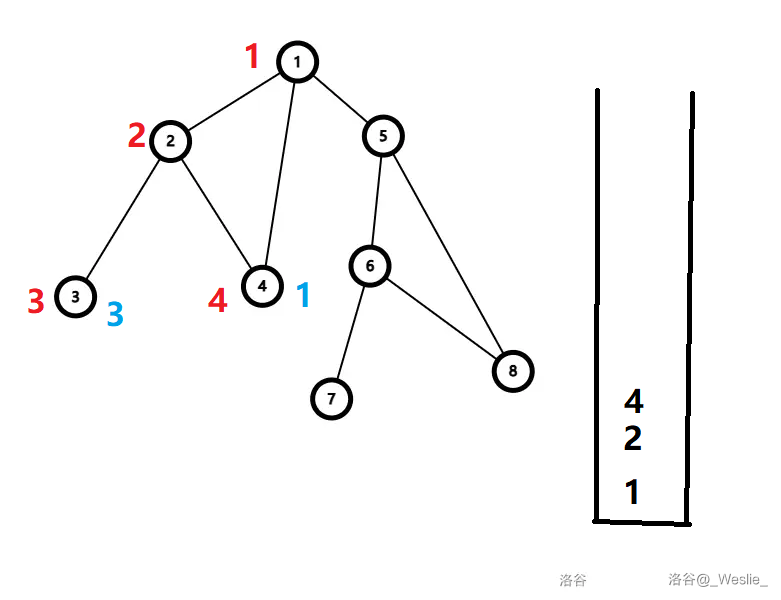
回溯到 $2$,记录 $low_2=1$。
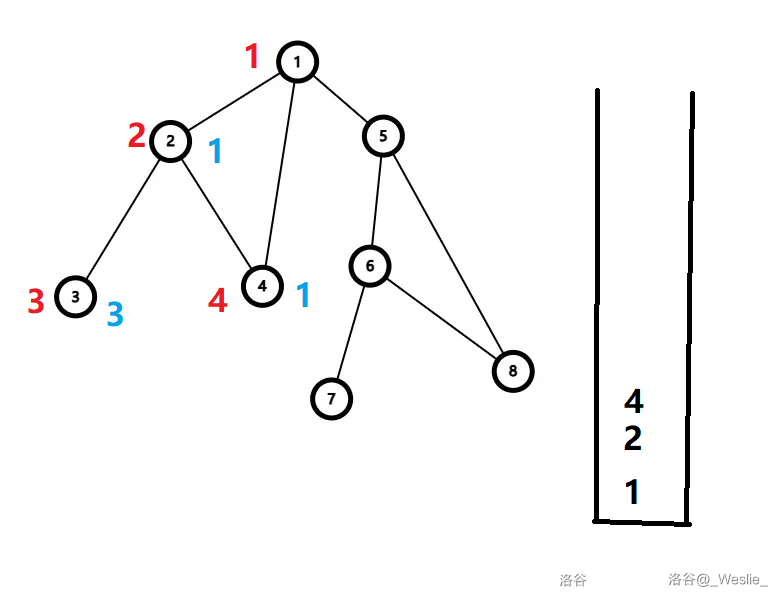
回溯到 $1$,然后遍历 $5,6,7$。
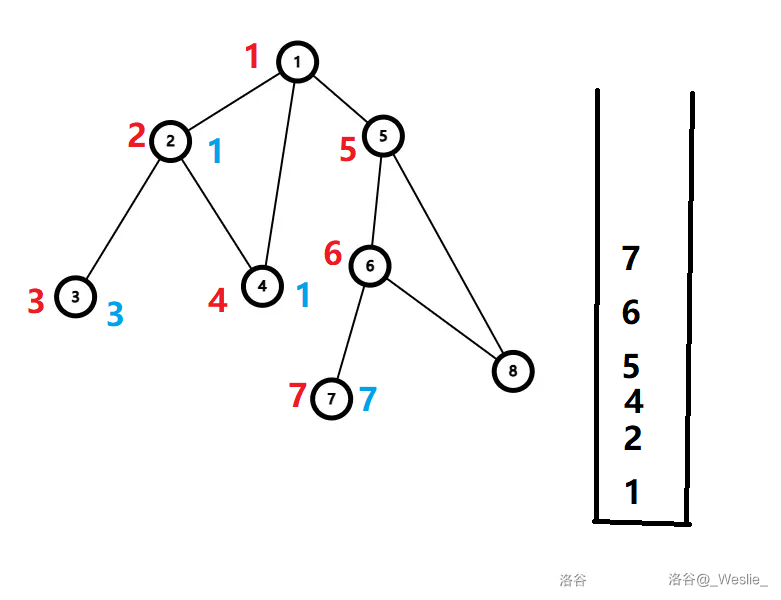
发现 $low_7=dfn_7$。于是 $7$ 出栈,自己成为一个边双连通分量。$7$ 与其祖先的这一条边就是割边。
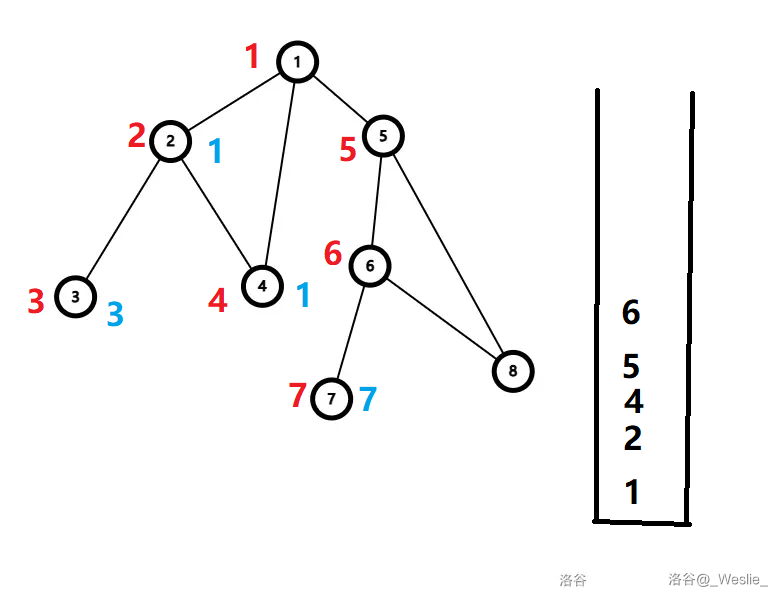
回溯到 $6$,遍历 $8$,记录 $low_8=5$。
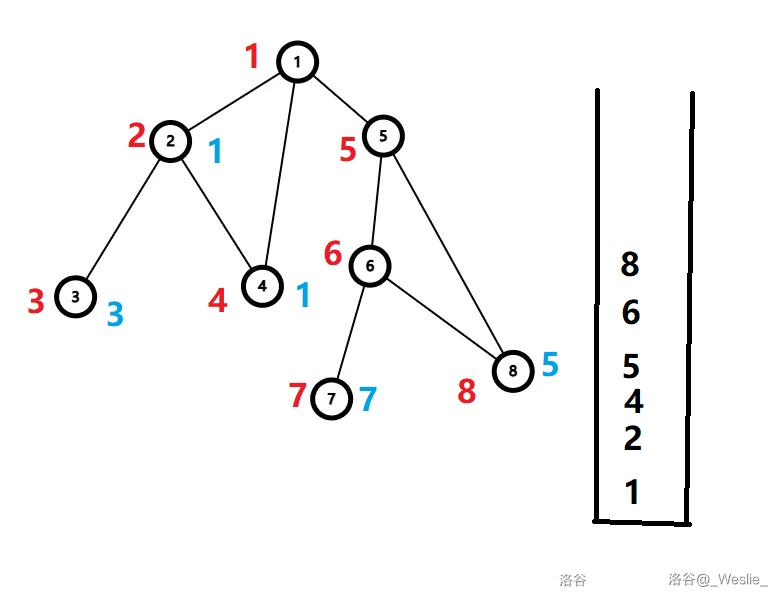
继续回溯,发现 $low_5=dfn_5$,于是 $\{5,6,8\}$ 一起出栈。$5$ 与其祖先的边成为割边。
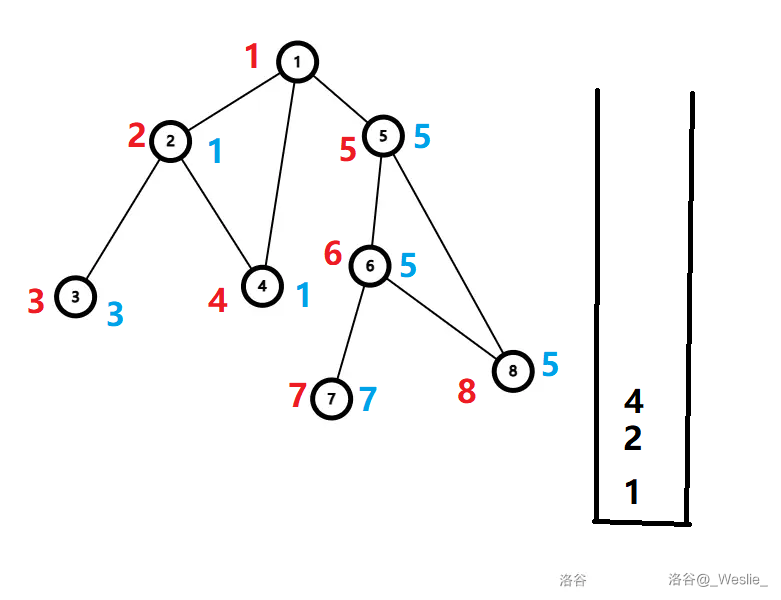
这样最后得到 $low_1=1$,然后把 $\{1,2,4\}$ 出栈。
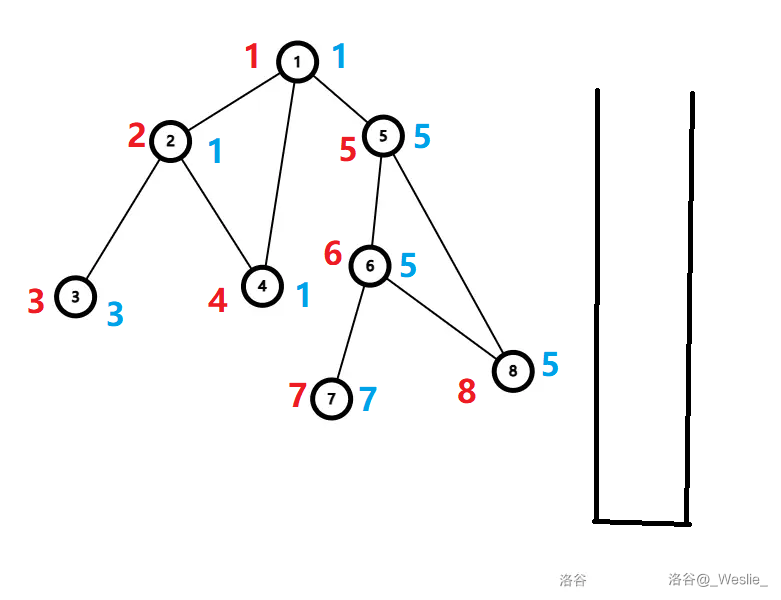
这样得到四个边双连通分量:$\{3\}$、$\{7\}$、$\{1,2,4\}$、$\{5,6,8\}$。
割边有三条,即下图中红色的边。
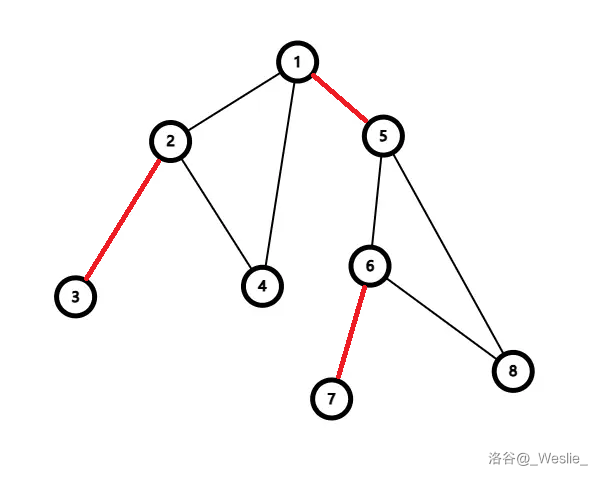
完成!
#### 代码实现
```
void dfs(int now,int fa){
dfn[now]=++idx;low[now]=idx;
st.push(now);
for(int i=head[now];i;i=e[i].nxt){
if(!dfn[e[i].v]){
dfs(e[i].v,e[i].id);
low[now]=min(low[now],low[e[i].v]);
}
else{
if(e[i].id!=fa)low[now]=min(low[now],dfn[e[i].v]);
}
}
if(low[now]==dfn[now]){
c.clear();
tot++;
while(!st.empty()){
int v=st.top();st.pop();
c.push_back(v);
if(v==now)break;
}
sort(c.begin(),c.end());
for(int i=0;i<c.size();i++){
g[tot].push_back(c[i]);
}
//如果你要求割边,这里直接记录 fa 是割边即可
}
}
```
#### 题目练习
- [P8436 【模板】边双连通分量](https://www.luogu.com.cn/problem/P8436)
- [P2860 [USACO06JAN] Redundant Paths G](https://www.luogu.com.cn/problem/P2860)
- [P2783 有机化学之神偶尔会做作弊](https://www.luogu.com.cn/problem/P2783)
这些题也在配套题单中有收录。
割边在主题库没有模板,这里提供一道私题:[U582665](https://www.luogu.com.cn/problem/U582665)。
### 割点和点双连通分量的求法
这一部分比较复杂,尤其是点双连通分量。因为一个点可以出现在多个点双连通分量中。
#### 点双连通分量的性质
- 两个点双最多只有一个公共点,且一定是割点。
- 对于一个点双,它在 dfs 搜索树中 $dfn$ 值最小的点一定是割点或者树根。
在接下来的讲解中,你可以验证这两个性质。
#### 文字叙述
我们利用 Tarjan 算法求出一张图的割点(点双连通分量)的过程如下:
1. 遍历 $u$,初始化。
2. 遍历 $u$ 的邻居 $v$。
- 如果 $v$ 是 $u$ 的儿子,那么遍历 $v$ 来求出 $low_v$。如果 $low_v\ge dfn_u$,说明 $u$ 是一个割点。然后弹空 $u$ 还残存在栈中的子树(注意!不要把 $u$ 弹出去),这些点构成一个点双连通分量。
- 如果不是,那么就按无向图的 $low$ 定义处理 $low_u\leftarrow\min(low_u,dfn_v)$。
3. 这一步割点和点双略有差异。
- 点双:这个简单。只要判断 $u$ 这个点是不是单独一个连通块就可以了(如果是那 $u$ 自己就是一个点双)。
- 割点:稍微难办一点:我们在第二步记录一个儿子的数量。如果 $u$ 是根节点,那么它必须有 $2$ 个儿子才是一个割点;否则因为都有父亲,所以有 $1$ 个儿子就行。
#### 图解
文字叙述还是太过于抽象了。我们用图来描述一下这个过程(点左侧的红色数字为 $dfn$,右侧的蓝色数字为 $low$)。
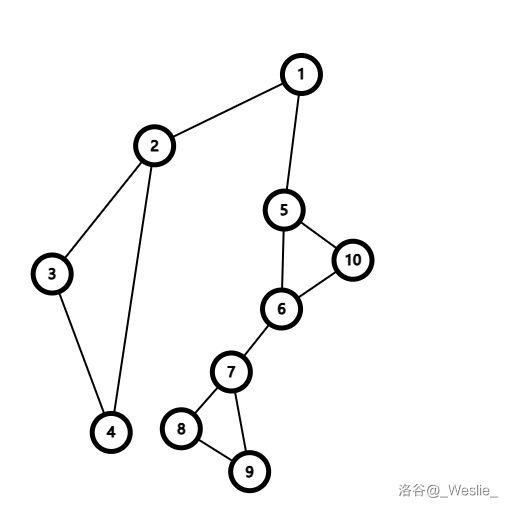
首先,遍历点 $1,2,3,4$,得到 $low_4=2$。
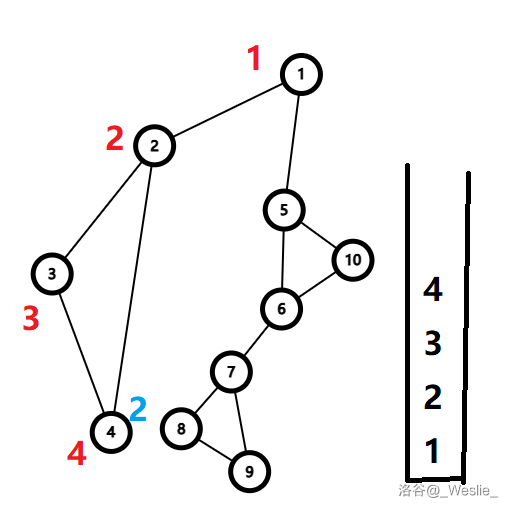
回溯到 $2$。发现 $low_2=2$,$2$ 是割点,于是把 $3,4$ 弹出栈,$\{2,3,4\}$ 构成一个点双连通分量。
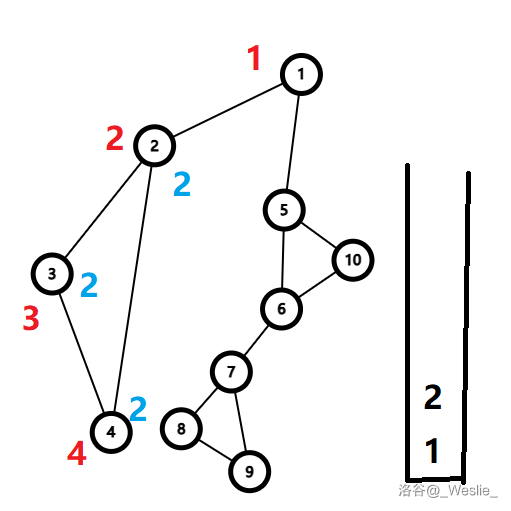
然后回溯到 $1$。发现 $low_2\ge dfn_1$,于是把 $2$ 弹出栈,$\{1,2\}$ 构成一个点双连通分量。
然后继续遍历 $5,6,7,8,9$,处理出 $low_9=7$。
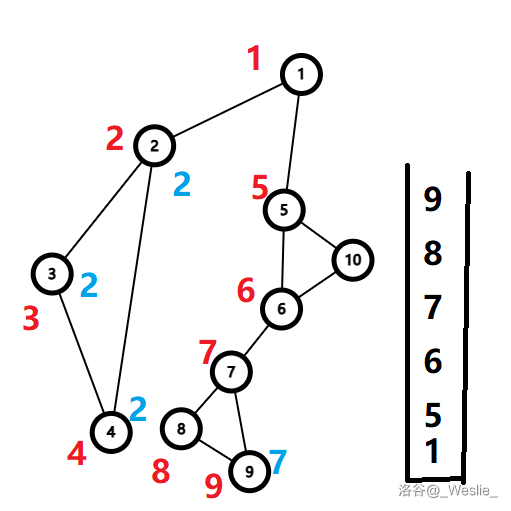
回溯发现 $low_8\ge dfn_7$,所以 $8,9$ 出栈,$7$ 是割点,$\{7,8,9\}$ 构成一个点双连通分量。
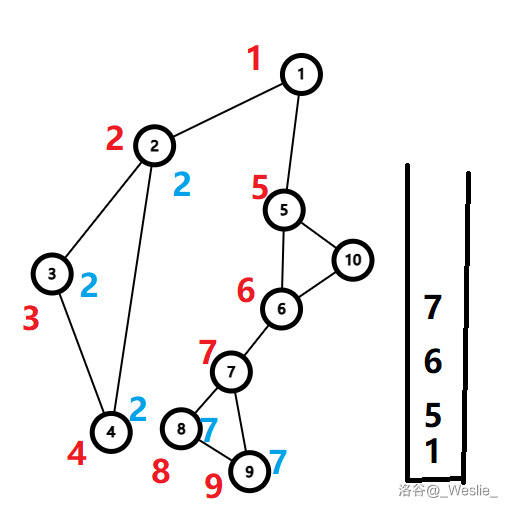
继续回溯,发现 $low_7\ge dfn_6$,于是 $7$ 出栈,$\{6,7\}$ 为一个点双连通分量($6$ 是割点)。
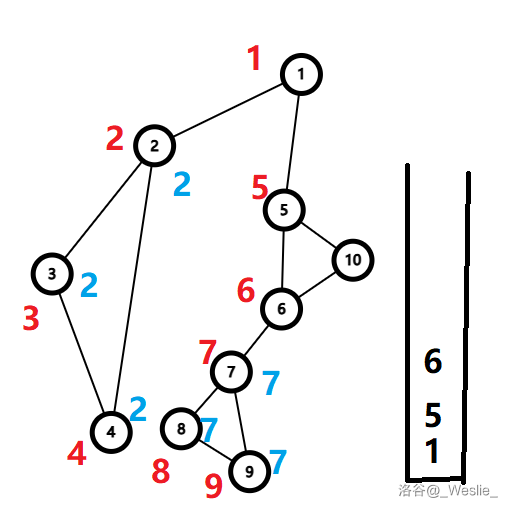
遍历点 $10$,处理 $low_{10}=5$。
然后回溯($6$ 到 $10$ 这一块图比较抽象,见谅)。
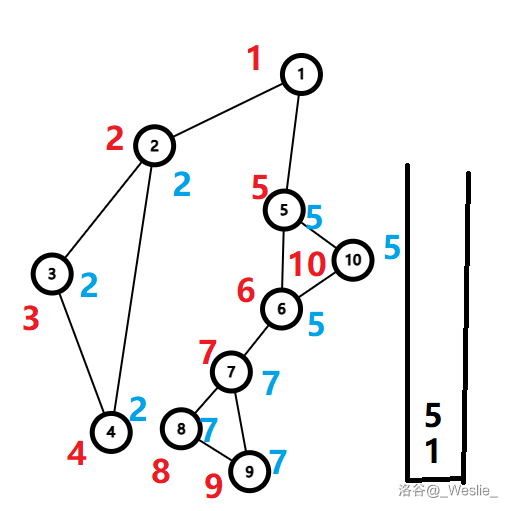
注意到 $low_6\ge dfn_5$,于是 $6,10$ 出栈,$\{5,6,10\}$ 是一个新的点双连通分量($5$ 是割点)。
继续回溯,发现 $low_5\ge dfn_1$,于是 $5$ 出栈,$\{1,5\}$ 是一个新的点双连通分量。由于 $1$ 有多于 $2$ 个儿子,所以 $1$ 是割点。
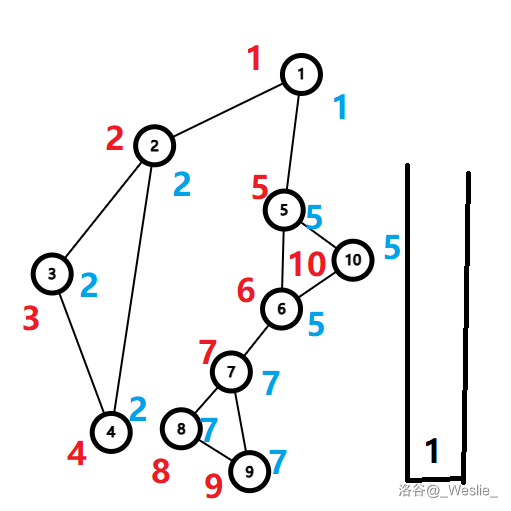
完成!
得到 $6$ 个点双连通分量:
- $\{2,3,4\}$;
- $\{1,2\}$;
- $\{1,5\}$;
- $\{5,6,10\}$;
- $\{6,7\}$;
- $\{7,8,9\}$。
#### 代码实现
##### 割点
```
void tarjan(int u,int fa){
low[u]=dfn[u]=++num;
int sum=0;
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(v==fa)continue;
if(!dfn[v]){
tarjan(v,u);
if(low[v]>=dfn[u]){
sum++;
}
low[u]=min(low[u],low[v]);
}
else low[u]=min(low[u],dfn[v]);
}
if(u==root)sum--;
if(sum>0)fl[u]=1,ans++;
return;
}
```
##### 点双
```
void dfs(int now,int fa){
int u=now,son=0;
low[u]=++idx;dfn[u]=idx;
st.push(u);
for(int i=head[now],v;i;i=e[i].nxt){
v=e[i].v;
if(!dfn[v]){
dfs(v,now);
son++;
low[u]=min(low[u],low[v]);
if(dfn[u]<=low[v]){
tot++;
while(!st.empty()){
g[tot].push_back(st.top());
if(st.top()==v){
st.pop();
break;
}
st.pop();
}
g[tot].push_back(u);
}
}
else{
if(v!=fa)low[u]=min(low[u],dfn[v]);
}
}
if(fa==0&&son==0){
g[++tot].push_back(u);
}
}
```
#### 例题
割点:
- [P3388 【模板】割点(割顶)](https://www.luogu.com.cn/problem/P3388)
- [UVA315 Network](https://www.luogu.com.cn/problem/UVA315)
- [P3469 [POI 2008] BLO-Blockade](https://www.luogu.com.cn/problem/P3469)
- [P3225 [HNOI2012] 矿场搭建](https://www.luogu.com.cn/problem/P3225)
点双连通分量:
- [P8435 【模板】点双连通分量](https://www.luogu.com.cn/problem/P8435)
- [B3610 [图论与代数结构 801] 无向图的块](https://www.luogu.com.cn/problem/B3610)
这些题目也是收录在配套题单中。
## 写在后面
本文章耗时两个晚上,共 $11150$ 字符,$471$ 行。
这篇文章不只是为了 [【图论】Tarjan 入门](https://www.luogu.com.cn/training/576466) 而写,更是为了在 CSP/NOIP 等比赛中赛前快速理解 Tarjan。
~~如果你觉得有收获,那就请留个赞再走吧。~~