对于一类期望问题的探讨
Maxwell_dcc
·
·
个人记录
特别鸣谢:@Graygoo
模拟赛中做到这样一题:(好毒瘤的 noip t2)
(n \le 10^5 , m \le 100 , p_i \le 100)
std
然后了解到这个问题有如下的弱化版:
P1654
(修改自第一篇题解)
对每一个 i 维护其期望贡献。
令 x_1[i] 为 x 的期望:x_1[i]=(x_1[i-1]+1) \times p_i。
令 x_2[i] 为 x^2 的期望:x_2[i]=(x_2[i-1]+2 \times x_1[i-1]+1) \times p_i。
则 x^3 的期望 ans[i]=ans[i-1]+(3 \times x_2[i-1]+3 \times x_1[i-1]+1) \times p_i,ans[n] 即为答案。
时间复杂度 O(nm^2)。
回到原题
现在我们拥有一个 O(n^2) 的暴力和一个 O(nm^2) 的期望递推。
$E(i,x)=p_i \times (\sum^{j \le x}_{j=1} \binom{x}{j} E(i-1,j)+1)$。
$ans[i]=p_i \times (\sum^{j \le m}_{j=1} \binom{m}{j} E(i-1,j)+1)+(i-p_i) \times ans[i-1]$。
- $O(nm)$ 正解:
考虑 $ans[i]=ans[i-1]+p_i \times \delta$。
($\delta=\sum^{j<m}_{j=1} \binom{m}{j} E(i-1,j)+1$)
我们使用 $\text{stirling}$ 变换处理下降幂。
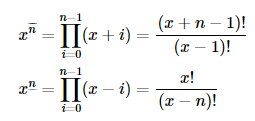

([来源](https://www.cnblogs.com/Wild-Donkey/p/16110498.html))
使用如上的方法可以将复杂度降至 $O(nm)$。
## 类似的问题,更高效的解法 by Graygoo
求以最后一个音符结尾的极长连续段 $m$ 次方期望。
solution:
