『从入门到入土』串串学习笔记
Hoks
·
·
算法·理论
目录
- 0.前言
- 1.附题单
- 2.KMP
- 2.1.前缀函数
- 2.1.1.定义
- 2.1.2.计算
- 2.2.KMP 算法
- 2.2.1.模板
- 2.2.2.Password 模板+思维
- 2.2.3.Power Strings 典中典
- 2.2.4.Writing a Song KMP 转移 dp
- 2.2.5.Prefix Function Queries KMP 自动机
- 2.2.6.P9606 [CERC2019] ABB KMP 求最长回文子串
- 2.2.7.P3426 [POI2005] SZA-Template KMP+dp
- 2.2.8.P3502 [POI2010] CHO-Hamsters KMP+矩阵优化 dp
- 2.2.9.P5829 【模板】失配树 KMP+LCA
- 2.2.10.The Supersonic Rocket 计算几何+KMP
- 2.3. Border Theory
- 2.3.1. 结论与证明
- 2.3.2. P1393 Mivik 的标题 Border Theory 模板运用
- 2.4.后记
- 3.Hash
- 3.1.定义
- 3.2.实现
- 3.3.应用
- 3.3.1.P3375 【模板】KMP Hash 不可做
- 3.3.2.P9606 [CERC2019] ABB 大力 Hash
- 3.3.3.P3501 [POI2010] ANT-Antisymmetry Hash+二分
- 3.3.4.P3538 [POI2012] OKR-A Horrible Poem Hash 求最短循环节+质因数分解优化
- 3.3.5.Matrix Matcher 二维 Hash
- 3.3.6.P3763 [TJOI2017] DNA 可以失配 k 次的字符串匹配问题
- 3.3.7.P3449 [POI2006] PAL-Palindromes 美妙结论+Hash
- 3.3.8.P3546 [POI2012] PRE-Prefixuffix dp+Hash
- 3.4.后记
- 4.Trie
- 4.1.定义
- 4.2.实现
- 4.3.应用
- 4.3.1.P4407 [JSOI2009] 电子字典 trie+dfs
- 4.3.2.P6088 [JSOI2015] 字符串树 可持久化 trie
- 4.4.后记
- 5.Manacher
- 5.1.算法思想与实现
- 5.2.应用
- 5.2.1.P9606 [CERC2019] ABB Manacher 做法
- 5.2.2.P4287 [SHOI2011] 双倍回文 Manacher 好题
- 5.2.3.P6216 回文匹配 Manacher+KMP
- 5.3.后记
- 6.Z 函数(扩展 KMP)
- 6.1.算法思想与实现
- 6.2.应用
- 6.2.1.P5410 【模板】扩展 KMP/exKMP(Z 函数)
- 6.2.2.Prefixes and Suffixes 和 Division + LCP (hard version)
- 6.2.3.P7114 [NOIP2020] 字符串匹配 Z 函数与循环节
- 7.ACAM
- 7.1.定义
- 7.2.实现
- 7.3.应用
- 7.3.1.[P3966 TJOI2013] 单词 Fail 树板题
- 7.3.2.P4052 [JSOI2007] 文本生成器 ACAM 上 dp
- 7.3.3.P2444 [POI2000] 病毒 ACAM+dfs 找环
- 7.3.4.P2414 [NOI2011] 阿狸的打字机 Fail 树+BIT
- 7.3.5.Death DBMS ACAM+树剖!
- 7.3.6.P2336 [SCOI2012] 喵星球上的点名 思路转化+Fail 树+BIT
- 7.3.7.[GEN - Text Generator] ACAM +矩阵优化 dp
- 7.3.8.String Set Queries 可持久化 ACAM
- 7.3.9.Duff is Mad/P7582 「RdOI R2」风雨(rain) 根号相关的 ACAM
- 7.3.10.[P8571 JRKSJ R6] Dedicatus545 ACAM+虚树
- 7.4.后记
- 8.SA
- 8.1.定义
- 8.2.实现
- 8.3.SA 与 LCP
- 8.4.应用
- 8.4.1.PHRASES 最长不重叠出现子串
- 8.4.2.P4070 [SDOI2016] 生成魔咒 SA+字符串翻转
- 8.4.3.P3975 [TJOI2015] 弦论 SA 求第 k 小子串
- 8.4.4.P3181 [HAOI2016] 找相同字符 SA+单调栈
- 8.4.5.P3649 [APIO2014] 回文串 SA+Manacher+ST 表
0.前言
写这篇文章的初衷是仿照树剖博客,串联的讲完有关串串的大部分 \mathrm{OI} 中会用到的算法。
因为是 『从入门到入土』,所以,这篇文章将会 \mathrm{Hash,KMP} 开始,讲到 \mathrm{SAM,PAM} 结束。
P.S.:本文中的字符串下标均从 1 开始,有关树的根节点均为 0。
那么,在正式开始前,还是致谢:
- 感谢从各个方面给我帮助的神犇 lzyqwq。
- \mathrm{Hash} 题单中的众多好题正是搬运自 lsj2009 的 \mathrm{Hash} 题单。
- \mathrm{ACAM} 题单的前身便是 abruce 的 \mathrm{ACAM} 题单喵,他详细描述的题单真的非常好。
- \mathrm{manacher} 题单来自于 Shiota_Kaede 喵。
- 感谢旻偲指出 Power Strings 中证明部分的错误。
- 感谢postpone指出 3.3.1 节中错误的做法。
1.附题单
『基础篇』KMP系列
『从入门到入土』哈希
『进阶方法篇』manacher
『进阶方法篇』Z 函数
『提高进阶篇』ACAM
『究极折磨挑战篇』SA,SAM,PAM
如果要收藏的话麻烦收藏原题单喵。
2.\mathrm{KMP}
\mathrm{KMP} 算法用于解决字符串匹配问题,其本质是使用了前缀函数。
所以本块将先介绍前缀函数。
2.1.前缀函数
2.1.1.定义
对于长度为 n 的字符串 s,其前缀函数是一个长度为 n 的数组 \pi。
定义 \pi_i 为子串 s_1\sim s_i 的最长相等真前后缀。
其中后面这个部分,也就是字符串 s 的相等真前后缀,叫做 border。
那么定义 \pi_i 为子串 s_1\sim s_i 的最长 border。
写成数学式子也就是:
\pi_i=k(s_1\sim s_k=s_{n-k+1}\sim s_n \& s_1\sim s_{k+1}\not=s_{n-k}\sim s_n)
特别的,规定 \pi_1=0。
举例而言,对于字符串 syxsyxqwq:
$\pi_2=0$,因为 `sy` 没有 $border$。
$\pi_3=0$,因为 `syx` 没有 $border$。
$\pi_4=1$,因为 `syxs` 的最长 $border$ 为 `s`,长度为 $1$。
$\pi_5=2$,因为 `syxsy` 的最长 $border$ 为 `sy`,长度为 $2$。
$\pi_6=3$,因为 `syxsyx` 的最长 $border$ 为 `syx`,长度为 $3$。
$\pi_7=0$,因为 `syxsyxq` 没有 $border$。
$\pi_8=0$,因为 `syxsyxqw` 没有 $border$。
$\pi_9=0$,因为 `syxsyxqwq` 没有 $border$。
同理可以计算 `abcabca` 的前缀函数为 $[0,0,0,1,2,3,4]$。
--------------------
### 2.1.2.计算
首先不难发现,**两个相邻的前缀函数 $\pi_i,\pi_{i+1}$ 的值至多加 $1$。**
考虑我们已经求出了 $\pi_i$,要求 $\pi_{i+1}$。
其最优情况一定是 $s_{\pi_i+1}=s_{i+1}$,也就是 $\pi_{i+1}$ 由 $\pi_i$ 转移过来。
此时 $\pi_{i+1}=\pi_i+1$,即为至多相差 $1$。
接着来考虑怎么求 $\pi$ 数组。
设我们目前已经求出了 $1\sim i$ 的所有 $\pi_i$,要求 $\pi_{i+1}$。
这个时候,就要考虑 $s_{1\sim i}$ 这个子串的 $border$ 与 $s_{1\sim i+1}$ 这个子串的 $border$ 的关系。
显然的是 $s_{1\sim i+1}$ 的 $border$ 只有 $s_1=s_{i+1}$ 产生的长度为 $1$ 的新 $border$ 和从 $s_{1\sim i}$ 的 $border$ 转移过来的两种可能性。
我们先尝试 $s_{1\sim i}$ 的最长 $border$,也就是 $\pi_i$ 能否转移,可以的话 $\pi_{i+1}=\pi_i+1$。
那如果不行的?那我们就要去找到一个次长 $border$ 尝试匹配。
这个时候就要用到一个经典性质:**$border$ 的 $border$ 还是 $border$**。
这里给张图来方便理解:
下图中的 $j=\pi_{\pi_i}$。
$\overbrace{\underbrace{s_1,s_2,\dots,s_j}_j,s_{j+1},\dots,s_{\pi_i}}^{\pi_i},s_{\pi_i+1},\dots,s_{n-\pi_i},\overbrace{s_{n-\pi_i+1},\dots,s_{n-j},\underbrace{s_{n-j+1},\dots,s_n}_j}^{\pi_i}
又因为 \pi_i 表示的是子串 s_{1\sim i} 的最长 border,所以 \pi_{\pi_i} 即为其次长 border。
按照这个匹配上退出,失配一直跳的思路,我们便得到了求前缀函数的代码。
void getnxt(char s[],int n,int nxt[])
{
for(int i=2,j=0;i<=n;i++)
{
while(j&&s[i]!=s[j+1]) j=nxt[j];
if(s[i]==s[j+1]) j++;nxt[i]=j;
}
}
2.2.\mathrm{KMP} 算法
学会了如何求前缀函数,接着来考虑运用。
\mathrm{KMP} 算法便是前缀函数的一个经典运用。
2.2.1.模板
考虑经典例题 P3375【模板】KMP。
比较简单的是第二问,第二问答案即为 \pi 数组。
接着来考虑第一问。
假设我们已经处理到了文本串 s 的第 i 位,而此时模板串 t 匹配到了第 j 位。
首先考虑如果下一位能匹配上,那就直接匹配。
即为:if(s[i]==t[j+1]) j++;。
那如果不能匹配,考虑失配如何跳转。
因为我们要能匹配上的是最长的,并且在移动模式串后文本串仍能匹配上。
那这是什么呢?
不就是最长的 border 吗。
所以,考虑匹配不上时,跳转到 \pi_j。
匹配部分代码如下:
for(int i=1,j=0;i<=m;i++)
{
while(j&&s[i]!=t[j+1]) j=nxt[j];
if(s[i]==t[j+1]) j++;
if(j==n) print(i-n+1),puts(""),j=nxt[j];
}
其中 nxt 即为 \pi。
附上 std。
2.2.2.Password 模板+思维
这题的简化题意就是:
- 求给定字符串的一个子串,使得这个子串既是前缀,又是后缀,而且在字符串中(非前后缀)出现过。或者输出无解。
-
首先考虑即是前缀又是后缀,这个非常简单,也就是 border。
接着考虑如何保证这个字符串在中间也出现过。
考虑 \pi_n 表示 s_{1\sim n} 的最长 border 长度,正是 s_{1\sim \pi_n}=s_{(n-\pi_n+1)\sim n}。
而 \pi_i 表示 s_{1\sim i} 的最长 border 长度,也就是 s_{1\sim \pi_i}=s_{(i-\pi_i+1)\sim i}。
那么如果 \pi_n=\pi_i,也就是 s_{(n-\pi_n+1)\sim n}=s_{1\sim \pi_n}=s_{(i-\pi_i+1)\sim i}。
那么在这个连等式中,第一个就是后缀,第二个为前缀,第三个就是中间出现过的了。
也就是,问题被转化为了找到一个 \pi_i=\pi_n。
但是,真的是这样的吗?
我们求的不一定是最长 border 啊,可能是其他的 border,也可以符合题意啊。
那么考虑 \pi_n 能否匹配,如果能那就输出解,否则跳转至 \pi_{\pi_n}。
那这样判断是否有解的话,复杂度也是 n^2 的。
考虑构造一个字符串形如 aaa\dots aaa。
那么 \pi_i=i-1,\pi_n 的跳转次数便会达到 n 次,再加上每次扫一遍 \mathrm{O}(n),直接 T 飞。
考虑前缀函数的性质:每次至多加 1!
这说明什么?
我们只需要得到 mx=\max\{\pi_i\},那么一直跳转 \pi_n 直到 \le mx 即可。
因为前缀函数一次至多加 1,所以想要变到 mx 的话,值为 0\sim mx 的 \pi 都存在。
代码也就非常精简了。
附上 std。
2.2.3.Power Strings 典中典
(修正了一些问题,感谢旻偲指出错误。)
简化题意:
这里是一个重要结论,需要掌握证明。
结论即为,循环节当且仅当 (n-\pi_n)\mid n 时存在,且最短循环节为 n-\pi_n。
下面给个证明:
首先这个结论是对 border 成立的,但是不为最短循环节。
也就是对于一个长度为 m 的 border,当且仅当 (n-m)\mid n 时为循环节。
考虑把字符串复制一份对齐原串的 border 结尾,就得到了:
s_1,s_2,\dots,s_m,s_{m+1},\dots~\dots~\dots~\dots,s_n
~~~~~~~~~~~~~~~~~~~~~~~~s_1~,s_2,\dots,s_m,s_{m+1},\dots,s_{n-m},s_{n-m+1},\dots,s_n
(不是很对齐,见谅。)
其中 border 就是对其的那两段:s_{m+1\sim n},s_{1\sim n-m}。
显然的是上下 s_{1\sim m} 都是相同的,
又因为上下对齐的部分也是相同的(因为是 border)。
所以 s_{1\sim m}=s_{m+1\sim 2\times m}。
类比上面的过程一直循环往前推,就能一直推到 s_{1\sim m}=s_{(k-1)\times m+1\sim k\times m}(k\times m\le n\&(k+1)\times m>n)。
那这样的话,最后字符串还会剩下 s_{k\times m+1\sim n} 或是为空。
如果存在这一段的话,长度 len<m,所以这个 border 便不是循环节。
也就是只有为空的时候才是循环节。
也就是 (n-m)\mid n 时才为循环节。
接着来证明 \pi_n 这个 border 求出来的是最短循环节。
这个就很简单了,因为 \pi_n 是最长的 border,而 border 越长,n-m 就越短,所以求出来的就是最短循环节了。
但这里还有个不严谨的地方,就是如何证明 (n-\pi_n)\nmid n 时 ,肯定没有更长的循环节。
考虑反证法,假设有更长的循环节(长度为 k)能满足条件,而 n-\pi_n 不能满足条件。
递推一下就可以得到 s_{\pi_n+1\sim k}=s_{n-k+1\sim n-\pi_n}。
也就是这个长度为 k 的循环节也是个 border,且长度 k>\pi_n。
类似于上图的做法,考虑对其一下,就能得到:
可能最小段+附加段=附加段+可能最小段。
那么这个段就是可以继续找到循环节分割的。
分割后的串长度肯定是小于等于最小可能段长的。
如果分割出的段和最小可能段一样,那么根据题设是不行的。
如果分割出的段比最小可能段还小的话,和最小可能段的定义矛盾了,也是不行的。
也就是当 (n-\pi_n)\nmid n 时,不存在长度 <n 的循环节。
(这一段一定要好好理解再自己证明一遍!)
附上 std。
\LARGE{练习题}
P4391 [BOI2009] Radio Transmission
这道题和上面那道题基本没有区别。
附上 std。
P3435 [POI2006] OKR-Periods of Words
略微提升一二的题目。
附上 std。
2.2.4.Writing a Song \mathrm{KMP} 转移 \mathrm{dp}
简要题意:
- 给定长度为 n 的字符串 t,构造一个字符串 s,使得在给定位置出现/不出现字符串 t。
-
考虑设计一个 \mathrm{dp}:
转移的时候枚举下一位的字符,用 **$\mathrm{KMP}$** 跑失配考虑找到最优的 $j$(这里不再赘述)。
因为这题要输出的是方案,所以 $\mathrm{dp}$ 过程中记得记录下转移路径。
附上 [std](https://www.luogu.com.cn/paste/n59zdzlk)。
**$\LARGE{练习题}$**
[Word Cut](https://www.luogu.com.cn/problem/CF176B) 和 [[ABC284F] ABCBAC](https://www.luogu.com.cn/problem/AT_abc284_f)
双倍经验思考题喵。
附上 [std](https://www.luogu.com.cn/paste/8ac9vdjo)。
[P8112 [Cnoi2021] 符文破译](https://www.luogu.com.cn/problem/P8112)
略微提升的练习题。
附上 [std](https://www.luogu.com.cn/paste/dvbavcwz)。
[CF1015F Bracket Substring](https://www.luogu.com.cn/problem/CF1015F)
稍微难点的题,但其实也还好。
[题解](https://www.luogu.com.cn/article/fjt0t5cl)。
--------------
### 2.2.5.[Prefix Function Queries](https://www.luogu.com.cn/problem/CF1721E) **$\mathrm{KMP}$** 自动机
简要题意:
> - 给定长度为 $n$ 的字符串 $s$,$q$ 次询问,每次询问给定字符串 $t$,长度为 $m$,求 $s+t$ 这个字符串最靠右的 $m$ 个前缀的 $border$ 长度。
> - $n\le10^6,q\le10^5,m\le10$。
考虑每次把新的串接上去对新的部分跑 $\mathrm{KMP}$。
但这样的复杂度仍然是 $\mathrm{O}(nqm)$。
考虑 $\mathrm{KMP}$ 自动机:
定义 $lst_{i,j}$ 表示表示第 $i$ 个前缀的所有 $border$ 中,最长的使得下一位刚好是 $j$ 的位置,当 $s_{i+1}=j$ 时 $lst_{i,j}=i$,否则 $lst_{i,j}=lst_{\pi_i,j}$。
这样就完成此题了。
附上 [std](https://www.luogu.com.cn/paste/ghr8hywv)。
-------------------------
### 2.2.6.[P9606 [CERC2019] ABB](https://www.luogu.com.cn/problem/P9606) **$\mathrm{KMP}$** 求最长回文子串
简要题意:
> - 给定一个长度为 $n$ 的字符串,问最少要在末尾添上多少个任意字符才能使他变为回文串。
>
> - $n\le 4\times10^5$。
这个题用 **$\mathrm{Hash}$** 写非常简单暴力,但是这里我们来思考 **$\mathrm{KMP}$** 做法。
对于任意的一个字符串 $s$,设其反串(就头尾翻转)为 $ss$。
显然的是 $s+ss$ 肯定是一个回文串。
接着考虑 $s+ss$ 这个串他有多少多余不必的字符。
比如 $s$ 为 `syxx` 时,$ss$ 为 `xxys`。
此时 $s+ss$ 为 `syxxxxys`,但是显然的我们只需要把 $s$ 补为 `syxxys` 即可。
这个时候观察下我们省略掉的部分,正是 `xx`,也就是字符串 $s$ 的最长回文后缀。
那么直接来大胆猜一手结论:省略掉的部分便是字符串 $s$ 的最长回文后缀。
首先证充分性:
考虑把字符串 $s$ 分给为 $s'+t$,其中 $t$ 为最长回文后缀,且令 $ss'$ 为 $s'$ 的反串。
那么显然的是 $s'+t+ss'$ 为回文串。
也就是答案 $ans\le n-|t|$。
接着来证必要性:
考虑反证法,假设有个更小的 $ans$ 满足条件。
那么显然的是 $s_{1\sim ans}$ 是非回文串,而 $s_{ans+1\sim n}$ 为回文串。
但是 $t$ 已经是最长回文后缀了,所以 $n-ans\le|t|$,即为 $ans\ge n-|t|$。
但是根据假设得: $ans<n-|t|$。
所以矛盾,命题得证。
接着就来考虑如何求最长回文后缀了,这里考虑用 **$\mathrm{KMP}$**。
因为要求的是最长回文后缀,所以考虑把 $ss+s$ 拼起来作为新的字符串。
但是这样可能会有问题,因为求得的 $border$ 长度可能会 $>n$。
所以考虑在中间加入非字符集内字符的方法拼接,新字符串即为:$ss+\#+s$。
这样再跑一次 **$\mathrm{KMP}$** 求出 $\pi_{2\times n+1}$ 即为最长回文后缀。
附上 [std](https://www.luogu.com.cn/paste/88u7rmtk)。
$\LARGE{练习题}
Extend to Palindrome
EPALIN - Extend to Palindrome
这两题都是经验了,输出方案的话随便改改上面那题就过了。
2.2.7.P3426 [POI2005] SZA-Template \mathrm{KMP}+\mathrm{dp}
简要题意:
虽然同是 \mathrm{KMP}+\mathrm{dp},这题的难度可比前面那题高多了。
首先前缀函数 \pi 肯定是得先弄出来的,接着考虑怎么 \mathrm{dp}。
设计一个 \mathrm{dp}:f_i 表示长度为 i 的前缀的答案,那最后的答案即为 f_n。
接着来考虑怎么转移,不难发现 f_i 只可能有两种取值 i,f_{\pi_i}。
因为如果能用一个长度更短的字符串反复覆盖成 s,至少要能覆盖它的最长 border。
考虑下什么时候 f_i=f_{\pi_i}。
那必然是在 i-\pi_i\sim i 存在一个 j 使得 \pi_j=\pi_i。
具体实现用个桶即可。
然后就可以得到超短的核心代码:
for(int i=2;i<=n;i++) f[i]=(h[f[nxt[i]]]>=i-nxt[i])?f[nxt[i]]:i,h[f[i]]=i;
剩下部分代码好像没必要放了。
2.2.8.P3502 [POI2010] CHO-Hamsters \mathrm{KMP}+矩阵优化~\mathrm{dp}
简要题意:
- 给出 n 个互不包含的字符串,要求你求出一个最短的字符串 S,使得这 n 个字符串在 S 中总共至少出现 m 次,问 S 最短是多少。
-
考虑 dp。
设计 f_{i,j} 表示填了 j 个串,结尾第是 i 个串的最短长度。
那么转移即为:
f_{i,j}=\min(f_{k,j-1}+w(k,i))
其中 w(k,i) 表示在 k 这个字符串后接 i 要多接多少字母。
那么 w(k,i) 的计算就非常一眼了,即为 i 的长度减去 k 的尾部和 i 的头部重复的字母数。
后面这个部分可以直接对字符串跑 KMP 算出来。
这样我们就得到了一个 O(n^2m) 的做法。
发现 m 很大,考虑用矩阵优化递推优化到 O(n^2\log m)。
不难发现,如果我们把每个字符串看做一个点,字符串拼接看做是点间的边。
那么这个题就相当于是在一张 n 个点的图上走 m 步,问最短路长度。
这个就显然是可以用矩阵来做的,矩阵乘法一次就相当于是做了一遍 floyd,所以乘个 m 次快速幂优化下就行。
附上 std。
\LARGE{练习题}
P3193 [HNOI2008] GT考试 \mathrm{KMP}+矩阵优化~\mathrm{dp}。
P1393 Mivik 的标题 上一道题的再升级加强。
突然发现题目编号好相似。
2.2.9.P5829 【模板】失配树 \mathrm{KMP}+\mathrm{LCA}
简要题意:
考虑 \mathrm{KMP},通过跳两个前缀的 \pi 求得所有 border。
思考一下这玩意像什么?
如果把一个字符串看做一个点的话,这个跳 \pi 的过程就是在树上跳。
而求最长公共 border 不就是找两条往上跳的路径的第一个交点吗?
这玩意在树上叫啥来着?
这不就 \mathrm{LCA} 吗。
所以考虑对着 \pi 建出 \mathrm{Fail} 树,在 \mathrm{Fail} 树上求 \mathrm{LCA} 就行了。
其实我个人是更偏向于树剖的,不过代码是以前的代码,就用倍增了。
附上远古抽象马蜂的 std。
\LARGE{练习题}
XYD 的 2023 年 CSP-S 的模拟赛的 T4 挺好的。
P2375 [NOI2014] 动物园 貌似是纯板子?
2.2.10.The Supersonic Rocket 计算几何+\mathrm{KMP}
简要题意:
- 平面上给定两个点集,判定两个点集分别形成的凸多边形能否通过旋转、平移重合。
- 点集大小 n\le 10^5,值域 [0,10^8]。
题意里都直接给计算几何摆出来也是够抽象的。
那没办法了,先计算几何吧。
不会的自行跳转:P2742 [USACO5.1] 圈奶牛Fencing the Cows /【模板】二维凸包。
个人感觉学个 Andrew 应该够了。
然后题意变成了判断两个凸包是否同构。
此时我们就要进行条件的转化。
如何把一个二维的图形等价为一个一维的信息?
我们考虑全等。
两个凸包在什么条件下是全等的?
边和夹角都相等。
那如何把这东西表示出来呢?
这时我们想到万能的向量。
使用点积表示出夹角就行了(注意不能使用叉积)。
对于整个凸包我们依次存下来边长和夹角绕一圈就行了。
因为凸包是可以转圈的,所以我们的这个序列也是一个环状的。
现在就变成了判断两个字符串是否循环同构了。
考虑直接 KMP 即可。
唯一需要注意的点就是当心角度搞出来 nan 了,记得判下改为 eps 即可。
代码可以见 CF1017E 解题报告喵。
\LARGE{练习题}
P3454 [POI2007] OSI-Axes of Symmetry
求对称轴数,这里的夹角就可以用叉积规避掉 nan 了喵。
2.3. \mathrm{Border~Theory}
其实 \mathrm{Border~Theory} 就是一些关于 border 的强结论,但是用出来太牛了,所以单独开了一个部分。
2.3.1. 结论与证明
首先介绍什么是 \mathrm{Border~Theory}。
定理 0:如果 i 是 s 的一个 border,那么 |s|-i 是 s 的一个周期。
这个证明就是前面那个 Power Strings,不再赘述。
定理 1(弱周期定理,Weak Periodicity Lemma,WPL): 若 i,j 都是 s 的一个周期,且 i+j\le|s|,则 \gcd(i,j) 也是 s 的一个周期。
这个证明是简单的。
我们考虑把这个划分的图画出来。
那么就可以发现如果我们把上下两部分作差,中间差出来的那个部分也是一个周期。
也就是对于任意的 k>0,只要满足 ix-jy=k 有整数解,则能取到是一个周期。
由裴蜀定理我们知道 k 肯定是 \gcd(i,j) 的倍数,最小值也就是 \gcd(i,j)。
在此之上还有推论(强周期定理,Periodicity Lemma,PL):若 i,j 都是 s 的一个周期,且 i+j-\gcd(i,j)\le|s|,则 \gcd(i,j) 也是 s 的一个周期。
定理 2:对于 s 的所有长度 len\ge \lfloor\frac{|s|}{2}\rfloor 的 border,它们与 |s| 构成一个等差数列:
我们不妨先设 s 的两个 border~x,y 满足 len\ge \lfloor\frac{|s|}{2}\rfloor。
由定理 0,我们可知 |s|-x,|s|-y 是 s 的两个周期。
然后因为 x,y 满足 len\ge \lfloor\frac{|s|}{2}\rfloor,所以我们可以根据定理 1 得到 d=\gcd(n-x,n-y) 是 s 的周期。
那么显然的是 d,2d,3d,\dots 都是 s 的周期,所以 |s|-d,|s|-2d,|s|-3d,\dots 都是 s 的 border。
显然的是这与 |s| 组成了一个公差为 d 的等差数列。
而因为我们知道定理 1 是一个下界,所以不可能存在其他长度的 border 满足上述限制。
证毕!
定理 3:将所有 border 按其二进制最高位进行分段,每一段内的 border 都构成一个等差数列。
证明类似于定理 2。
对于最高位由定理 2 我们知道是对的。
接着我们对一个长度段 [2^{i-1},2^i],2^i\le |s| 证明。
假设他有个最长 border 为 t,那么由定理 2 我们知道 t 与 2^i 和剩下的所有 border 形成了一个等差数列,公差为 2^i-t。
那么结合下前面最高位是对的,也就证明完了定理 3
也就是说,对于一个字符串 s,其所有 border 构成 O(\log |s|) 个等差数列。
这就是非常美妙的性质了,意味着如果我们可以一次维护一个等差数列就可以把维护所有 border 的复杂度变对。
通过定理 3 我们还能证明出一个推论:对于一个串 s,所有公差 \ge d 的等差数列个数 \le\lfloor\frac{|s|}{d}\rfloor。
2.3.2. P1393 Mivik 的标题 \mathrm{Border~Theory} 模板运用
简要题意:
- 在一个有 m 个不同按键的键盘上随机打 n 个字符,问产生的字符串包含字符串 S 的概率。
-
可以见题解喵。
暴力的想法,可以直接上矩阵,思路直接像 GT 考试一样写,那么复杂度是 O(|s|^3n) 显然爆飞了。
可以很容易发现这题的重点肯定是在 n 上了,比起 GT 考试小了许多。
直接上来考虑设计 dp。
我们设 f_i 表示 [i-|s|+1,i] 恰好为 s 且这是 s 第一次出现。
那么我们知道答案是 \sum\limits_{i=|s|}^n f_i\cdot m^{n-i}。
接着就是计算 f_i 了,不难发现,我们先固定 [i-|s|+1,i],那么剩下的部分直接乱填,方案数是 m^{n-i-|s|}。
接着考虑来去重。
-
这样的出现显然是完整和目前新造这段不重的。
方案数也很好数,即为 $\sum\limits_{j=0}^{i-|s|}f_j\cdot m^{i-|s|-j}$。
-
这样就是前面的一段拼上 $s$ 的一段前缀成了一个新的 $s$。
那这个前缀肯定是 $s$ 的一个 $border$。
找到所有的 $border~j$ 进行转移就行了。
方案数就是 $\sum\limits_{j} f_{i-|s|+j}$。
然后我们就知道现在要做的是什么了。
转化下题意。
现在就是给一个数组末尾加,然后对于一个位置 $i$ 给定 $n$ 个定值求这些 $i$ 减去这些定值的位置之和。
这东西看着就很不可做,但是这 $n$ 个定值之间有联系。
根据 border theory,我们知道这 $n$ 个定值可以划分为 $\log n$ 个等差数列。
考虑对于每个等差数列维护,直接做前缀和就可以做到 $O(n\log |s|)$。
也就是正常的前缀和是从 $-1$ 的位置转移,等差数列用 $-k$(其中 $k$ 为公差)转移即可。
代码可以见[题解](https://www.luogu.com.cn/article/dx2hjv2r)喵。
----------------
### 2.3.3.[P4156 [WC2016] 论战捆竹竿](https://www.luogu.com.cn/problem/P4156) $\mathrm{Border~Theory}$ 的进阶运用
简要题意:
> - 给定一个字符串 $s$,定义字符串 $t$ 初始为 $s$,每次可以选择一个位置满足后缀与 $s$ 前缀相同的位置开始接上 $s$。
> - 问 $t$ 串长度集合中 $\le w$ 的长度种类数。
> - $T\le5,|s|\le5\times10^5,w\le10^{18}$。
看着就很有意思啊。
首先我们知道,每次拼接就是去掉一个 $border$ 然后接上 $s$。
换个角度考虑问题,因为不管怎么接了之后最后面结尾总是能截取出一个完整的 $s$。
所以我们不妨直接考虑每次多接上的长度的值。
那么接上的长度就是 $|s|-|st|$,其中 $st$ 为 $s$ 的一个 $border$。
先跑一遍 $\mathrm{KMP}$ 求出所有 $border$,就可以得到所有的 $|s|-|st|$。
设得到的这个值为一个长为 $m$ 的序列 $x$,我们的问题就变成了求这个式子:
$$\sum\limits_{i=1}^ma_i\cdot x_i=k(0\le k\le w-n),\forall a_i\ge 0$$
其中的 $k$ 可取值数量即为答案。
这个东西就是一个[同余最短路的板子](https://www.luogu.com.cn/problem/P3403)。
具体的显然有 $k$ 若能表示,那么 $k+x_1,k+2\times x_1,\dots,k+n\cdot x_1$ 是可以被表示的。
我们钦定 $x$ 是按照降序排序的,那么我们取 $x_1$ 为模数,用剩下的数连边。
$k\rightarrow (k+x_i(2\le i\le m))\bmod x_1
这样建模之后我们从 0 开始跑一遍最短路,跑到的 d_i 的意义就是最小的能达到 \bmod x_1\equiv i 的 d_i。
那么对于 d_i\le w-n,对答案的贡献就是 \lfloor\frac{w-n-d_i}{x_1}\rfloor+1,这点计数显然。
但因为 border 数量是 O(n) 的,所以我们图的边数是 O(n^2) 的,跑 dijkstra 的话无法避免遍历边集,无论如何也没法通过。
那只能从 border 的性质下手了。
由前文我们知道 \mathrm{Border~Theory}。
这个定理最为厉害的地方就在于把 border 划分为了 O(\log n) 个等差数列。
考虑把每个等差数列合起来一次做掉来保证复杂度。
那现在我们要做的就是一次加入一个等差数列的长度的边,维护最短路。
如何让加入等差数列的复杂度变对?
考虑到我们成环本质是无意义的,所以我们只要剥环就行了。
假设公差为 d,取当前的首项 x 为模数,那么就会成 \gcd(x,d) 个环,尝试对每个环做。
新的问题就有了,那么就是最短路的源点不确定了,枚举多源肯定完了。
不难发现边权都是正的,所以环上的最小点显然是不会被更新的,以这个为源点左右拓展即可。
具体的,我们考虑用单调队列实现,直接单调队列的 dp 掉一个环就行了。
接着就剩下最后一个问题了,如何更换模数?
对于假设我们要从模数 x 换到 y,数组 f 换到数组 g。
考虑下本身的意义就是在最小能到达取模模出 i 的位置。
显然的我们可以用 f_i 更新 g_{f_i\bmod y}。
但此时注意到,长度为 x 的转移被我们忽略掉了,所以记得再跑一遍补上就行了。
最后的答案计算就和上面一样。
至此我们完成了这道题。
2.4.后记
\mathrm{KMP} 部分到这里就告一段落了,剩下的可以去看看题单练习练习喵。
别问我为什么没有高维的讲解,我不会喵。
3.\mathrm{Hash}
\mathrm{Hash},永远的神!
\mathrm{Hash} 可以在 \mathrm{O}(1) 的时间判断两个字符串是否相等,因为这个特性,他可以在时间复杂度仅劣 \log(n) 的情况下,从码量和理解难度方面薄纱 \mathrm{SA} 等算法。
\mathrm{Hash} 非常重要,所以这一块一定要落实喵。
3.1.定义
定义对于一个长度为 n 的字符串 s,其 \mathrm{Hash} 函数为:
f(s)=\sum\limits_{i=1}^ns_i\times base^i(\bmod M)
其中 base 为定义的倍数,M 为定义的模数。
不难发现这样的话 \mathrm{Hash} 函数的值域为 1\sim M-1,而字符串的种类数是很可能会比这个值域还大的。
也就是,对于两个不一样的字符串,我们也会得到相同的 \mathrm{Hash} 函数值。
这种情况,称之为 \mathrm{Hash} 冲突。
一般来讲,\mathrm{Hash} 冲突会导致 WA。
而在一道题目的数据下是否会 \mathrm{Hash} 冲突,就取决于选择的模数以及倍数了。
在可选择时,倍数会取 131,1331,13331,233 等。
而模数会取 10^9+7,10^9+9,998244353。
个人而言有两个比较推荐的模数 1004535809,167772161,来自于 mrsrz 的一篇题解中,强度高于前面给的三个。
但是切记,选择的 base,M 一定要满足 (base,M)=1。
因为如果 (base,M)\not=1 时,极容易发生 \mathrm{Hash} 冲突。
3.2.实现
根据上面 \mathrm{Hash} 函数的定义,可以很简单的用代码实现:
inline int hsh(char s[],int n)
{
int h=0;
for(int j=1;j<=n;j++) h=(h*op+s[j])%mod;
return h;
}
这个函数代码就已经可以通过 P3370 【模板】字符串哈希了。
但是在实际使用的时候,我们几乎不会这样算 \mathrm{Hash}。
考虑下这样的 \mathrm{Hash} 有什么缺点:
如果每次用到的都只是原本字符串里的一个子串的 \mathrm{Hash},就得在线 \mathrm{O}(n) 算了,效率非常低下。
但是 \mathrm{Hash} 有非常美妙的性质:可加性。
既然有可加性,那能联想到什么?
前缀和!
那这样的话,\mathrm{Hash} 的实现就成了:
inline void hsh(char s[],int n,int&h[])
{
for(int j=1;j<=n;j++) h[j]=(h[j-1]*op+s[j])%mod;
}
那使用前缀和后,就可以支持任意子串查询了。
正常的前缀和查询是 h_r-h_{l-1},那么 \mathrm{Hash} 函数的前缀和也是这样的吗?
并不是的,实则为 h_r-h_{l-1}\times base^{r-l+1}。
为什么是这样的呢?
考虑 \mathrm{Hash} 函数就是把一个字符串转化为一个 base 进制的数再把他映射到 0\sim M-1 这个值域里。
那么两个 base 进制的数相减,肯定要高位对齐才能得到低位喵。
又因为是 $base$ 进制数,所以要乘上 $base^{r-l+1}$。
一般在写的时候会先预处理出来 $base^1\sim base^n$ 为 $op_1\sim op_n$。
那么查询一段的 **$\mathrm{Hash}$** 值即为:
```cpp
inline int gethash(int h[],int op[],int l,int r){return ((h[r]-h[l-1]*op[r-l+1])%mod+mod)%mod;}
```
这里需要加上 $M$ 再对 $M$ 取模是因为可能会减出负数。
至此,就掌握了最基础的 **$\mathrm{Hash}$**。
--------------------------
## 3.3.应用
**$\mathrm{Hash}$** 的运用非常之多,所以被称为神。
因为本篇文章的重点在串串上,所以重点讲字符串 **$\mathrm{Hash}$**,剩下在题单中出现的字符串不相关题一概不出现。
------------------------
### 3.3.1.[P3375 【模板】KMP](https://www.luogu.com.cn/problem/P3375) **$\mathrm{Hash}$** 不可做
**勘误:因为 $border$ 不具有单调性不能二分,所以 **$\mathrm{Hash}$** 并不能在正确的复杂度做出此题第二问。**
考虑第一问,第一问直接考虑大力扫,先预处理出 $t$ 的 **$\mathrm{Hash}$** 值。
然后对于每个 $i$,找出 $i$ 往后的 $|t|$ 个字符的 **$\mathrm{Hash}$** 值比较一下是否相同即可。
接着考虑第二问,因为 $border$ 长度**不具有单调性**。
也就是长度更小的 $border$ 不存在时可能存在更长的 $border$。
所以 **$\mathrm{Hash}$** **并不能**用来求每个前缀的最长 $border$。
但通过 **$\mathrm{Hash}$** 我们可以求出整个串的所有 $border$。
具体而言,枚举 $border$ 长度然后首尾截出来判断一下是否相同就可以了。
------------
### 3.3.2.[P9606 [CERC2019] ABB](https://www.luogu.com.cn/problem/P9606) 大力 **$\mathrm{Hash}$**
其实这题用 **$\mathrm{Hash}$** 做就非常简单了,比前面讲的 **$\mathrm{KMP}$** 做法简单多了。
考虑直接枚举回文对称中心为 $i$,接着思考怎么 $check$。
显然的是现在的字符串 $s$ 就可以分成:
$s_1,\dots,s_i,s_{i+1},\dots,s_n,s_{n+1},\dots
显然的是后面从 n+1 开始的字符都是随意定的,所以对称过去之后肯定是能匹配上的。
那么需要考虑的就是以 i 分界向右到 n 这段是否和左边的字符串对称了。
考虑处理出正反 \mathrm{Hash} 值,直接把这两段拿出来比较即可。
附上 std。
3.3.3.P3501 [POI2010] ANT-Antisymmetry \mathrm{Hash}+二分
简要题意:
- 给定一个长度为 n 的 0/1 字符串 s,求其中异或意义下回文的子串数量。
-
首先观察题面,发现这个对称是在异或意义下的,那么不难得出要求的串的长度一定为偶数。
这个结论也很好证明,如果是奇数的话异或一下这个位置绝对会不同,自然不可能对称。
接着来考虑怎么做,发现直接 \mathrm{Hash} 不是很好处理,那就再次想到二分。
考虑对于每个点 i,二分其向右能拓展几位,接着再用 \mathrm{Hash} check 即可。
附上超远古抽象马蜂 std。
\LARGE{练习题}
STC02 - Antisymmetry
双倍经验喵。
3.3.4.P3538 [POI2012] OKR-A Horrible Poem \mathrm{Hash} 求最短循环节+质因数分解优化
简要题意:
- 给出一个长度为 n 的字符串 s,q 次询问,查询 s 某个子串的最短循环节。
-
首先需要了解的是 \mathrm{Hash} 如何求最短循环节。
如果存在长度为 i 的循环节,怎么判断呢?
考虑把字符串复制一份然后扣掉第一份尾部 i 个字符和第二份头部 i 个字符,就得到了:
s_1,s_2,\dots,s_i,s_{i+1},\dots,s_{n-i}
~~~~~~~~~~~~~~~~~~~~~~~s_{i+1},\dots,s_{n-i},s_{n-i+1},\dots,s_n
那如果存在长度为 i 的循环节,这两部分显然是相等的嘛。
原因就和前面那个 \mathrm{KMP} 的证明部分类似,这里不再赘述。
但是因为枚举效率十分低下,而且这玩意也没有单调性,貌似没法解决了?
注意到循环节长度肯定是子串长度的约数。
所以质因数分解再枚举下就行了。
附上 std。
3.3.5.Matrix Matcher 二维 \mathrm{Hash}
简要题意:
- 给定一个 n\times m 的矩阵 s 和一个 x\times y 的矩阵 t,询问 t 在 s 中出现了多少次,多测。
-
询问出现次数+小数据,难免让我们想到了枚举每个点 i,j 作为矩阵的左上角尝试和矩阵 t 匹配。
那如何快速匹配呢?考虑 \mathrm{Hash}。
但是貌似没有二维 \mathrm{Hash}?
没事,类比一维的定义一个就行。
我们定义二维 \mathrm{Hash} 函数为:
f(n,m)=\sum\limits_{i=1}^n\sum\limits_{j=1}^ms_{i,j}\times base_1^{n-i}\times base_2^{m-j}
因为是 \mathrm{Hash} 嘛,所以想要快速查询肯定得再套层前缀和。
再套个二维前缀和,那么这个时候,查询函数就成了:
f(x_2,y_2)-f(x_1-1,y_2)\times base_1^{x_2-x_1+1}-f(x_2,y_1-1)\times base_2^{y_2-y_1+1}+f(x1_1-1,y_1-1)\times base_1^{x_2-x_1+1}\times base_2^{y_2-y_1+1}
先给 \mathrm{Hash} 值扔一个数组里排个序,然后用 lower_bound,upper_bound 查询即可,这样就能避免桶。
3.3.6.P3763 [TJOI2017] DNA 可以失配 k 次的字符串匹配问题
简要题意:
- 给定长度为 n 的字符串 s 和长度为 m 的字符串 t,问在可以失配不超过 3 次的情况下 t 在 s 中出现了多少次。
- 多测,t\le10,n,m\le10^5 字符集仅有 A,T,C,G。
这种可失配匹配问题就是 \mathrm{Hash} 的专利了,\mathrm{KMP} 可做不了了。
首先考虑还是得先搞出来 \mathrm{Hash} 值。
接着考虑怎么处理这个最麻烦的失配。
发现失配次数给的不是很多,考虑枚举下失配,每次对这个区间二分得到第一个失配的点即可。
如果最后还没跑到 4 次就没失配了那肯定行的,如果第 4 次失配跑到区间外了也是行的。
判断一下直接扫一遍 s,对于每个位置 i,尝试 s_{i\sim i+m-1} 能否与 t 匹配即可。
附上 std。
3.3.7.P3449 [POI2006] PAL-Palindromes 美妙结论+\mathrm{Hash}
简要题意:
- 给定 n 个回文串,问将其两两拼接能得到多少的回文串(可以和自己拼接)。
-
首先给出第一个小结论一个回文串的循环节肯定是回文串,这里暂且省略证明。
接着是重点结论,当且仅当两个回文串的最小循环节相同时,他们才能拼成回文串。
首先证充分性:
考虑两个字符串 s,t,相同最小循环节为 s'。
设 s 由 x 个 s' 组成,t 由 y 个 s' 组成。
那么 x+y=\underbrace{s'+s'+\dots+s'}_{x+y}。
显然的是右边这部分是个回文串,充分性得证。
接着来证必要性:
考虑反证法,两个字符串 s,t,s 由 x 个 s' 组成,t 由 y 个 t' 组成,并且 x+y 是回文串。
不难发现,如果这个条件满足,那么 s' 即为 t' 的循环节。
但是 t' 已经是最短循环节了。
所以矛盾,必要性得证。
由此,我们得到了一个超强的结论。
接着用 \mathrm{Hash} 求最短循环节存下来,接着对每种计数就行了。
这点也非常简单,大力枚举就行。
详情可以见 std 喵。
3.3.8.P3546 [POI2012] PRE-Prefixuffix \mathrm{dp}+\mathrm{Hash}
简要题意:
- 定义循环相同为一个字符串移动后缀到首部与另一字符串相同。
- 给定长度为 n 的字符串 s,求 s 在循环相同意义下的最长 border。
-
考虑暴力:
我们枚举在字符串的首位删去等量字符。
然后求出剩余部分的最长 border。
如果删去的两段相等,那么就对于答案有贡献。
定义 f_i 表示删去 i 个字符后剩余部分的最长 border,则 f_i\le f_{i+1}+2。
这样我们就可以 \mathrm{O}(n) 求出 f 数组,接着用 \mathrm{Hash} 判断下 f_i 这个答案可不可取即可。
附上 std。
3.4.后记
\mathrm{Hash} 太深刻,太强大。
\mathrm{Hash} 的运用不止有字符串 \mathrm{Hash},还有异或 \mathrm{Hash},和 \mathrm{Hash} 等众多神兵利器。
剩下的部分,仍是考试热点,如 不可以总司令。
而且 \mathrm{Hash} 可以作为暴力劣正解一只 \log 的情况下拿分。
所以,还是要好好落实喵。
4.\mathrm{Trie}
在不与别的算法组合的情况下,串串中的 \mathrm{Trie} 貌似没有很多用法,所以这章与前面相比将会变的简短很多。
4.1.定义
\mathrm{Trie},中文名字典树,正如其名,就是一颗像字典的树。
为了方便讲解,这里先扔一张图:
CSA 画的,有点丑见谅。
可以看出来的是 \mathrm{Trie} 中,边的边权变成了一个字符,而从根节点 0 开始往下走路径上的字符就表示了一个字符串。
如 0\rightarrow 6 就组成了字符串 syxqwq。
感觉 \mathrm{Trie} 的结构貌似真的没什么好讲的?
其结构非常好理解,而一般的,我们用 \delta(u,c) 代表 u 节点走过 c 字符到达的节点编号。
4.2.实现
正常使用时,我们还要对每个点记录下他是否是一个字符串的结尾。
比如插入的字符串是 syxqwwq,实际上 \mathrm{Trie} 中有了的字符串有 s,sy,syx,syxq,syxqw,syxqwq。
此时如果来查询 syx,那么也会查询出存在的状态,所以要额外记录下是否是结尾。
下面给出 P8306 【模板】字典树 中插入字符串的代码:
int t;
int n,q,num;
int cnt[3000010],e[3000010][65];
char a[3000010];
int getnum(char c)//获得这个字符的编号
{
if(c>='A'&&c<='Z') return c-'A';
else if(c>='a'&&c<='z') return c-'a'+26;
else return c-'0'+52;
}
void insert()
{
int p=0,len=strlen(a);
for(int i=0;i<len;i++)
{
int c=getnum(a[i]);
if(!e[p][c]) e[p][c]=++num;//如果当前边状态不存在,就新建节点
p=e[p][c];cnt[p]++;//因为字符串可能重,所以用数组记下次数(其实对于这题重不重没区别)
}
}
接着有关 \mathrm{Trie} 的运用。
最基础也就是板子里的运用:查找一个字符串是否出现。
实现也非常简单,下面直接给出代码:
int query()
{
int p=0,len=strlen(a);
for(int i=0;i<len;i++)
{
int c=getnum(a[i]);
if(!e[p][c]) return 0;//如果不存在这个节点那肯定不存在
p=e[p][c];
}
return cnt[p];//如果出现次数为0那也是不存在
}
\LARGE{练习题}
P2580 于是他错误的点名开始了 纯板子,用于巩固。
4.3.应用
因为是串串相关,所以不会出现 0/1\mathrm{Trie} 喵。
例题也不是很多,就两道。
4.3.1.P4407 [JSOI2009] 电子字典 \mathrm{Trie}+\mathrm{dfs}
简要题意:
- 给定 n 个字符串 s_{1\sim n},q 次询问,每次询问给定字符串 t,询问 t 操作一次能变成 s_{1\sim n} 中的几个串。
- 操作有三种,分别为:
-
- 删除串中某个位置的字母;
-
- 添加一个字母到串中某个位置;
-
- 替换串中某一位置的一个字母为另一个字母。
-
查找字符串是否能匹配,这不就 \mathrm{Trie} 板子吗。
接着考虑操作一次,因为只能操作一次,所以想到了 dfs。
直接考虑每一步能否匹配,能匹配的话肯定不会浪费一次操作机会。
而如果失配的话,就尝试操作继续往下 dfs 就好了。
附上超远古 std。
\LARGE{练习题}
P2536 [AHOI2005] 病毒检测
和上面那题区别不大,不再赘述。
我拿 DFA 写的,就不放代码了。
4.3.2.P6088 [JSOI2015] 字符串树 可持久化 \mathrm{Trie}
看到剖就兴奋了。
简要题意:
- 给定一棵 n 个点的树,树上每条边为一个字符串,q 次询问,求出任意两个节点路径上有多少边代表的字符串以给定字符串为前缀。
-
树上路径查询,这可太经典了,假设查询的点是 u,v 答案为 ans(u,v)。
那么就有经典拆法:
ans(u,v)=ans(u,1)+ans(v,1)-2\times ans(\mathrm{LCA}(u,v),1)
然后问题就从路径转移到了一个节点到根节点的问题。
想到 \mathrm{Trie},但是每个节点到根节点的距离都开一个 \mathrm{Trie} 空间直接寄寄。
所以考虑可持久化。
这个可持久化就和线段树的可持久化没有太多区别嘛。
每次新增一个点只多了他到他父亲上的字符串,加进来即可。
每个节点一个版本,不就可持久化 \mathrm{Trie} 做完了嘛。
代码太丑了,不放了。
4.4.后记
光光用 \mathrm{Trie} 的串串题还是不多的,所以这个篇章也就这么长。
但是 \mathrm{Trie} 是非常重要的,一定需要掌握的。
因为,\mathrm{Trie} 会再次出现在 \mathrm{ACAM},广义 \mathrm{SAM},\mathrm{PAM} 中。
\mathrm{Trie}:请相信我们很快会再次相见的。
5.\mathrm{Manacher}
\mathrm{Manacher},在回文方面的利器。
代码简短线性复杂度,在回文的题目正常能吊打 \mathrm{KMP},\mathrm{Hash}。
因为是个算法而且基本没有额外定义,所以直接从例题开讲。
5.1.算法思想与实现
首先,我们要了解 \mathrm{Manacher} 能解决什么问题。
比如 P3805 【模板】manacher:
其简要题意即为:
这个字符串 s 的长度就非常吓人,达到了 10^7,也告诉我们一定要用小常 \mathrm{O}(n) 算法。
接着来看题目,题意非常精简:最长回文子串。
考虑这种东西怎么找?
可以从一个点 i 开始,考虑最多能往两边扩展多少格,再全部取个 \max 即为答案。
那么问题就转化成了对于每个 1\le i\le n,如何快速求出以其为中心的回文串长度。
珂以考虑 \mathrm{Hash}+二分,但是这样的复杂度是 \mathrm{O}(n\log n),理论不能通过此题。但这题数据有点水。
重点来讲讲正片 \mathrm{Manacher} 算法。
首先对于以 i 为对称中心的字符串分个类,就知道分为长度为奇/偶数两种。
不妨先考虑下长为奇数的回文子串如何求:
假设我们已经求出了 1\sim i 的每个点为对称中心的最长扩展长度 h_{1\sim i}。
接着来考虑怎么求 h_{i+1}。
假设我们现在已经求到的回文子串的最远右端点为 r。
这个时候又分为两种情况:
-
当 i\le r 时:
这个时候我们考虑利用已经求出来的字符串得到答案:
\dots ,\overbrace{s_l,\dots,\underbrace{s_{j-h_j+1},\dots,s_j,\dots,s_{j+h_j-1}}_{palindrome},\dots,\underbrace{s_{i-h_j+1},\dots,s_i,\dots,s_{i+h_j-1}}_{palindrome},\dots,s_r}^{palindrome},\dots
显然的是 l\sim r 为最长回文子串且包含 i 的时候, i 的最优情况是把另外半边与他回文的 j 的最右回文子串对称过来。
但是有一种可能性就是你对称过来之后 i+h_j-1>r,这个情况显然是不一定成立的,所以更新的值要和 r-i 取 \min。
-
当 i>r 时:
这个时候考虑直接用暴力头尾扩展回文子串。
记得拓展完后更新最右回文子串。
根据这个思想就可以很简单实现代码:
inline void manacher(char s[],int h[],int n)
{
for(int i=1,r=0,md=1;i<n;i++)
{
h[i]=i<=r?min(h[md*2-i],r-i):1;
while(s[i+h[i]]==s[i-h[i]]) h[i]++;
if(h[i]+i>r) r=h[i]+i,md=i;
}
}
这个时候就有个很棘手的事情,就是怎么处理偶数长度的回文串呢?
考虑在字符串中的每两个字符间插入 #,再在头部放一个 -(因为本文全是从 1 开始的,所以 0 不附特殊值可能寄)。
那这样的话所有偶数的情况都被转化为了奇数的情况,可以用上面那个代码处理。
而这步处理,只需要在读入的时候完成即可:
inline void red(char s[],int&n)
{
s[0]='-',s[++n]='#';s[++n]=getchar();
while(chk(s[n])) s[n]=getchar();
while(ck(s[n])) s[++n]='#',s[++n]=getchar();n--;
}
\LARGE{练习题}
P1723 高手过愚人节
双倍经验喵。
5.2.应用
\mathrm{Manacher} 算法的运用,貌似都是比较纯的套板子?
或许是因为我浅尝辄止导致的吧,但是这里给出的几道例题都不是很难喵。
5.2.1.P9606 [CERC2019] ABB \mathrm{Manacher} 做法
又是这个题!
这次我们来讲 \mathrm{Manacher} 算法。
类似于前面 \mathrm{KMP} 做法的思路转化,转化完后题意就成了:求最长后缀回文。
接着考虑怎么用 \mathrm{Manacher} 求最长后缀回文。
其实非常简单,就在板子上改一点,判断一下当前回文是不是延长到串尾了。
第一个延长到串尾的肯定是最长的,所以直接打断跳出去就行了。
附上 std。
练习题还是那两经验。
5.2.2.P4287 [SHOI2011] 双倍回文 \mathrm{Manacher} 好题
这题貌似乱搞做法一堆,还有一种正解是 \mathrm{Hash+PAM}。
但这里我们重点讲 \mathrm{Manacher}。
简要题意:
- 给定长度为 n 的字符串 s,求其最长双倍回文子串。
- 定义双倍回文为由两个一模一样的回文串组成的串。
-
首先我们可以很简单的得出普通的最长回文子串,直接上 \mathrm{Manacher} 就行了。
接着考虑怎么变成双倍回文。
这个时候贯穿 \mathrm{Manacher} 的朴素思想,直接考虑在更新 r 端点的时候尝试更新答案即可。
怎么尝试呢?
扫一下这个字符串看看他的左半边是不是回文串即可。
因为他本身是个回文串,所以他的左半边若是回文串,对称下右半边也就是回文串。
这样也就达成了双倍回文的条件。
具体实现可以参考第一篇题解。
复杂度是正确的,因为你把所有往右扫回文子串这个操作全部剥下来考虑。
不难发现其是单调的,所以直接朴素操作是线性的。
这样就完成了这题。
附上 std。
5.2.3.P6216 回文匹配 \mathrm{Manacher}+\mathrm{KMP}
简要题意:
- 给定长度为 n 的字符串 s 和长度为 m 的字符串 t,定义分数为一个字符串中 t 的出现次数。
- 问 s 所有回文子串的分数和。
-
看到回文子串,很快啊,直接先上个 \mathrm{Manacher} 再说。
然后考虑下怎么算这个逆天的分数。
因为是出现次数,所以先考虑对着 s,t 跑一遍 \mathrm{KMP} 得到所有的出现位置。
给这些位置标 1,然后加次前缀和,我们就可以很快的算出每个回文子串的分数,总复杂度是 \mathrm{O}(n^2)。
接着考虑如何优化。
考虑目前的前缀和数组是 s。
我们目前对于一个长回文串,做法是枚举他的每一个子串然后前缀和加上分数。
考虑从这个式子下手:
\sum\limits_{i=mid}^n\sum\limits_{l=mid}^{h_i}s_{i-l+m}-s_{i-l}=\sum\limits_{i=mid}^ns_{i-m+mid\sim i-m+h_i}-s_{i-h_i\sim i-mid}
其中 mid=\lceil{\frac{m}{2}}\rceil。
这个式子就可以二阶前缀和了,计算方法就是 ss_l+ss_r-2\times ss_{(r-l)/2}。
然后就完美完成了!
记得取模!
附上 std。
5.3.后记
在未学习 \mathrm{PAM} 这种逆天方法前,\mathrm{Manacher} 是最好用的有关回文的算法。(貌似还挺简单的?)
但是题目貌似真的不是很多,就当个方法掌握好了。
6.\mathrm{Z} 函数
个人感觉有点类似于 $\mathrm{Manacher}$ 的感觉,好像写起来也挺像的,所以放在 $\mathrm{Manacher}$ 板块后了。
求 $\mathrm{Z}$ 函数的方法,在国外被称为 $\mathrm{Z~Algorithm}$,在国内被称为 $\mathrm{exKMP}$ 或是**扩展** $\mathrm{KMP}$。
--------------------------------------
## 6.1.算法思想与实现
首先我们先定义什么是 $\mathrm{Z}$ 函数。
我们定义 $Z_i$ 表示**后缀 $i$ 与字符串原串的 $\mathrm{LCP}$ 长度**。
其实我们可以发现这个东西他和 $\mathrm{KMP}$ 是很相像的,不过 $\mathrm{KMP}$ 的前缀函数是定义在了 $border$ 结尾的位置,而 $\mathrm{Z}$ 函数是定义在了 $border$ 开头的位置。
这时我们就可以很清晰的看出它们之间的联系了。
我们对于 $\pi_i$ 计算贡献,就是对区间 $[i-\pi_i+1,i]$ 用一个首项为 $1$ 公差为 $1$ 的等差数列对每一位 $j$ 取 $\max$。
最终求得的序列的值就是 $\mathrm{Z}$ 函数的值。
但这样的话实现很 hard,还要跑 $\mathrm{KMP}$ 后面再上 $\mathrm{DS}$ 的。
所以我们考虑利用**自动机思想**来优化暴力得到更优的做法。
前面提到过 $\mathrm{Z}$ 函数和 $\mathrm{Manacher}$ 也很像,所以我们类似 $\mathrm{Manacher}$ 来思考。
假设我们要求 $Z_i$,现在已经知道了 $Z_{1\sim i-1}$。
首先特殊的,我们定义 $Z_1=0$。
考虑如何利用前面已经得到的信息?
那就是**把后面的新字符串尝试往前移动**,这点与 $\mathrm{Manacher}$ 是相同的。
具体的,我们记录下目前最右的匹配段为 $[l,r]$,这意味着 $s_j=s_{j+l-1},j\in[1,r-l+1]$。
那么我们用 markdown 画个图(假设 $r-l+1<l$ 这样方便点),大致就是长成这样:
$\overbrace{s_1,\dots,s_{r-l+1}},\dots,\overbrace{s_l,\dots,s_r},\dots,s_n
那么这两个被括号括起来的部分就是相等的。
然后我们考虑这东西和 i 有什么关系。
显然的是我们知道 l<i,因为 l 是取的前面已有的一个匹配段,必然是在 [1,i-1] 内的。
接着我们进行分类讨论,如果 i\le r,那么还是画图考虑。
\overbrace{s_1,\dots,\underbrace{s_{i-l+1},\dots,s_{r-l+1}}},\dots,\overbrace{s_l,\dots,\underbrace{s_i,\dots,s_r}},\dots,s_n
由于上括号划的这一段是相同的,所以下括号划的这一段显然也是相同的。
也就是在这种情况我们可以直接给 Z_i 赋值为 Z_{i-l+1}。
接着考虑超过去的情况。
直接暴力做即可!
具体的,我们对目前的这个算法进行复杂度分析。
如果看过 \mathrm{Manacher} 的分析,那么就会发现这东西完全没区别。
考虑对 r 进行分析,会发现 r 是单增的,每次成功的比较都会让 r+1,而不成功的都会让循环的 i+1。
所以总的复杂度就是 O(n),不过又是一个均摊算法。
对于代码实现,个人认为写的和 \mathrm{Manacher} 一样会比较好看好记好写不易挂。
inline void get_Z(char s[],int n,int z[])
{
for(int i=2,l=1,r=0;i<=n;i++)
{
z[i]=i>r?0:min(z[i-l+1],r-i+1);
while(i+z[i]<=n&&s[z[i]+1]==s[i+z[i]]) z[i]++;
if(i+z[i]-1>r) l=i,r=i+z[i]-1;
}z[1]=n;
}
6.2.应用
这个运用的话也没多少题,我努力找了下,唯一好一点的题还是 XYD 的题()。
所以可能没法提交只能看看题面想想题了()。
如果有我没收录的题欢迎私信供题喵。
6.2.1.P5410 【模板】扩展 KMP/exKMP(Z 函数)
简要题意:
- 给定字符串 s,t,求 t 的 \mathrm{Z} 函数,并求 s 以 t 为前缀的 \mathrm{Z} 函数。
-
首先第一问我们已经会了,现在的问题就是第二问。
对此我们有两种解决方法。
其实和 \mathrm{KMP} 求字符串匹配就是一样的嘛。
- 把 t 和 s 拼起来,中间插入特殊字符 \mathrm{Z} 函数,那么就可以直接得到两问的答案。
- 利用 t 的 \mathrm{Z} 函数重新跑一边求对于 s 而言的 ext。
其实和第一问事本质相同的,给 $s$ 已经求出来的一段 $[l,r]$ 本质就是映射到 $t$ 的 $[1,r-l+1]$ 了。
那这东西还是调用 $t$ 的 $Z_{i-l+1}$ 就可以了。
剩下的部分还是大力的**暴力拓展**就行了,复杂度很容易看出来还是均摊 $O(n)$ 的。
对于第二问的实现:
```cpp
inline void get_ext(char s[],char t[],int n,int m,int ext[],int z[])
{
for(int i=2,l=1,r=0;i<=m;i++)
{
ext[i]=i>r?0:min(z[i-l+1],r-i+1);
while(i+ext[i]<=m&&ext[i]<=n&&s[ext[i]+1]==t[i+ext[i]]) ext[i]++;
if(i+ext[i]-1>r) l=i,r=i+ext[i]-1;
}int j=0;while(j<=m&&j<=n&&s[j+1]==t[j+1]) j++;ext[1]=j;
}
```
------------------------------------
### 6.2.2.[Prefixes and Suffixes](https://www.luogu.com.cn/problem/CF432D) 和 [Division + LCP (hard version)](https://www.luogu.com.cn/problem/CF1968G2)
这两个题没多大意思所以直接塞一块讲了。
首先是 [Prefixes and Suffixes](https://www.luogu.com.cn/problem/CF432D)。
简要题意:
> - 给定一个字符串 $s$,求所有 $border$ 的出现位置和次数。
> - $1\le|s|\le10^5$。
直接从 $\mathrm{Z}$ 函数角度考虑。
$\mathrm{Z}$ 函数怎么求 $border$?
那么就是 $i+Z_i-1=|s|$ 的 $[i,|s|]$ 就是 $border$。
接着考虑数出现次数。
我们知道对于一个长度为 $l$ 的 $border$ 其出现位置就是 $[1,l]$。
再考虑下 $Z_i$ 的定义,就不难发现如果 $Z_i\ge l$ 则 $[i,i+l-1]$ 与 $[1,l]$ 相等,也就是出现一次。
然后问题就变成了数 $Z_i\ge l$ 的 $i$ 的个数,这个是很 ez 可以树状数组数的。
当然排序直接暴力单调数可以线性,不过我懒直接树状数组了。
[std](https://codeforces.com/contest/432/submission/290378279)。
然后是 [Division + LCP (hard version)](https://www.luogu.com.cn/problem/CF1968G2)。
简要题意:
> - 给定一个长度为 $n$ 的字符串 $s$。
> - 记 $f_k$ 为:把 $s$ **划分**成 $k$ 段,所以合法的划分方式中,这 $k$ 段的 $\mathrm{LCP}$ 的最大值。
> - 你需要对 $k\in[l,r]$ 求出 $f_k$。
> - $\sum n\le2\times10^5$。
显然的事不管怎么样肯定会有一个前缀串的。
所以我们可以利用 $\mathrm{Z}$ 函数辅助计算。
如果说长为 $j$ 是合法的,那么我们以 $j$ 尝试检验是否合法。
如果 $Z_i\ge j$,那么说明又出现了一次,直接 $i\leftarrow i+j$。
不如就 $i\leftarrow i+1$。
如果出现次数 $\ge k$ 那么就是可行的。
单调的去做,显然的是 $k$ 越大越不可行,所以我们从小枚举到大。
这个时候的 $j$ 就是单减的。
我们要实现一个快速的跳跃的过程,还要对不合法的 $Z_i$ 进行删除。
又因为这是个单调的过程,所以直接使用并查集实现即可。
[std](https://codeforces.com/contest/1968/submission/290353085)。
--------------
### 6.2.3.[P7114 [NOIP2020] 字符串匹配](https://www.luogu.com.cn/problem/P7114) $\mathrm{Z}$ 函数与循环节
简要题意:
> - 给定字符串 $s$,定义 $s^i$ 为 $i$ 个 $s$ 相接且 $w(s)$ 为 $s$ 中现**奇数次**的字符数量。
> - 问把 $s$ 拆分为 $(AB)^iC$ 且 $w(A)\le w(C)$。
> - $|s|\le2^{20}$,多测,$T\le 5$。
数据范围很吓人,感觉只能是一个线性/接近线性的东西。
首先我们先解决前面部分的 $(AB)^i$。
尝试对于每个长为 $i$ 的前缀考虑,假设前缀 $i-1$ 为 $AB$,我们计算 $(AB)^i$ 中 $i$ 的取值。
这个部分其实比较简单,我们直接画图看下 $\mathrm{Z}$ 函数的意义即可解决。
$\overbrace{s_1,\dots,s_{i-1},s_{i},\dots,s_{z_i}},\dots,s_{i+z_i-1},\dots,s_n
s_1,\dots,s_{i-1},\underbrace{s_{i},\dots,s_{z_i},\dots,s_{i+z_i-1}},\dots,s_n
划着括号的两部分显然是相同的,对齐的部分也显然是相同的。
那么我们就知道前缀 i-1 是前缀 i+z_i-1 的周期,也就是答案的取值即为 \lfloor\frac{z_i}{i}\rfloor+1。
然后我们考虑奇数次的限制。
前面的 i 个字符已经确定了,那么最后面的 C 也是可以确定的。
那么这个 $w(C)$ 只会有两种取值,因为循环节这段的贡献**只和选取数量的奇偶性有关**。
类似于异或,当循环节选取了两端之后其中的所有字符肯定都出现了偶数次,也就消掉没影响了。
更具体的,我们可以直接算出来这两种 $C$ 的个数分别为 $\lceil\frac{\lfloor\frac{z_i}{i}\rfloor+1}{2}\rceil,\lfloor\frac{\lfloor\frac{z_i}{i}\rfloor+1}{2}\rfloor$。
然后我们考虑计算这些情况下的 $A$ 的可能取值。
其实也就是大力分类讨论了,因为类似的 $A$ 本身也是和循环节次数有关的。
发现这个取值的值域其实很小,只有 $[0,26]$,直接用一个桶维护出前缀来做就可以做到 $O(26n)$。
当然可以用 BIT 来优化,做到 $O(n\log 26)$。
但这还是太劣了,我们想要线性!
发现其实维护前缀而言,每次多加入一个字母只会对一个值进行修改。
由此我们直接修改桶中的一个值就行了。
[std](https://www.luogu.com.cn/paste/qhev2c6k)。
---------------------------------
# 7.**$\mathrm{ACAM}$**
**$\mathrm{ACAM}$**,中文名 $\mathrm{AC}$ 自动机,全称 $\mathrm{Aho–Corasick(Alfred V. Aho, Margaret J. Corasick. 1975) Automaton}$。
要是概括什么是 **$\mathrm{ACAM}$** 的话,可以简单概括成:**$\mathrm{Trie}$** 上 **$\mathrm{KMP}$**。
解决的问题为:多模式串匹配问题。
如果忘了 **$\mathrm{Trie}$** ,**$\mathrm{KMP}$** 可以去看看喵:[Trie](#4),[KMP](#2)。
------------------
## 7.1.定义
这里先来介绍下什么是**自动机**。
确定性有限状态自动机(**$\mathrm{DFA}$**)一般简称为自动机,是一个被广泛运用的数学模型。
下面先给点定义:
1. **字符集($\Sigma$)**:自动机里包含的所有字符集合。
2. **状态集合($Q$)**:自动机中包含的状态集合。
3. **初始状态($start$)**:自动机的初始状态。
4. **接受状态集合($F$)**:自动机能接受的状态集合。
5. **转移函数($\delta$)**:状态与状态直接的转移的关系。
其实 **$\mathrm{Trie}$** 就是一个 **$\mathrm{DFA}$**,所以可以用 **$\mathrm{Trie}$** 的结构来理解起其定义。
转移函数就是图上的边,字符集就是边权的集合,状态集合就是点的集合,初始状态就是根节点,接受状态就是被打了结尾标记的点。
这样就大致了解什么是 **$\mathrm{DFA}$** 了,接着我们来讲 **$\mathrm{ACAM}$**。
首先其结构式基于 **$\mathrm{Trie}$** 的,所以有关结构的部分不再赘述。
重点在于其新增的东西:**$\mathrm{Fail}$** 指针。
考虑 **$\mathrm{ACAM}$** 解决的问题,本质还是字符串匹配。
所以考虑匹配时直接和 **$\mathrm{Trie}$** 相同往下走。
那如果失配了呢?就沿着 **$\mathrm{Fail}$** 指针跳转。
根据这点,**$\mathrm{Fail}$** 指针有什么性质呢?
他跳转的状态应该表示的是**当前状态的后缀**。
原因很简单,根据 $\mathrm{Trie}$ 的性质,我们在 **$\mathrm{Trie}$** 上匹配时就相当于在一路尝试匹配前缀。
那意味着,如果失配了,说明当前前缀都是不行的。
但是我们又要让文本串的匹配位置尽量靠前(不然就可能出现遗漏的情况)。
所以应该找到一个**在 $\mathrm{Trie}$ 状态中的当前匹配状态的最长后缀进行跳转**。
比较抽象所以下面举例说明:
假设我们的文本串为 `ssyxsyxqwq`,模式串有 `ssyxqwq` 和 `syxsyxqwq`。
那我们就可以对模式串先造出一颗 $\mathrm{Trie}$:
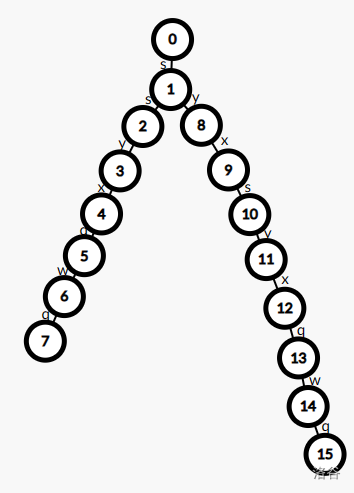
那么在 $\mathrm{Trie}$ 上先跑匹配的路线即为 $0\rightarrow1\rightarrow2\rightarrow3\rightarrow4$,匹配上了 `ssyx`。
接着发现没法匹配了,不难发现,我们的头是从文本串 $s_1$ 开始匹配的。
既然 $\mathrm{Trie}$ 无法匹配,就说明从 $s_1$ 开始的匹配已经不行了。
如果以朴素暴力的思想,那就从 $s_2$ 开始尝试前缀能否匹配。
这里也同理,找到已经匹配上 `ssyx` 这个串出现过的最长后缀。
发现了 `syx` 出现过,为 $9$ 号节点表示的状态,所以跳到 $9$ 号节点继续匹配。
此时匹配上的为 `syx`,然后沿着 $\mathrm{Trie}$ 的结构一路匹配就能匹配上模式串 `syxsyxqwq`了。
至此,我们了解了 $\mathrm{Fail}$ 指针的意义:**指向当前状态存在的最长后缀状态。**
接下来又是一个难题,如何求 $\mathrm{Fail}$ 指针?
既然这玩意他是 $\mathrm{Trie}$ 上 $\mathrm{KMP}$。
考虑和 $\mathrm{KMP}$ 一个思路:
假设我们现在已经求出了一个点 $v$ 他父亲 $u$ 的 $\mathrm{Fail}$ 指针并且建好了 $\mathrm{Trie}$ 树,且 $\delta(u,c)=v$。
1. 如果 $\delta(\mathrm{Fail}_u,c)$ 存在,那么 $\mathrm{Fail}_v=\delta(\mathrm{Fail}_u,c)$,退出循环。
2. 如果不存在,那么 $u=\mathrm{Fail}_u$。
3. 如果 $u=0$,那么 $\mathrm{Fail}_v=0$,退出。
4. 循环执行上述操作直到退出。
这个操作就相当于是在一个串和他的后缀后面同时加上字符 $c$。
下面放张对于下面那个样例构建 $\mathrm{Fail}$ 指针的 GIF。
(我尝试过画了,不过真的做不出来像样的箭头,所以转载下 OI-Wiki 的。)
模式串:`i`,`he`,`his`,`she`,`hers`。
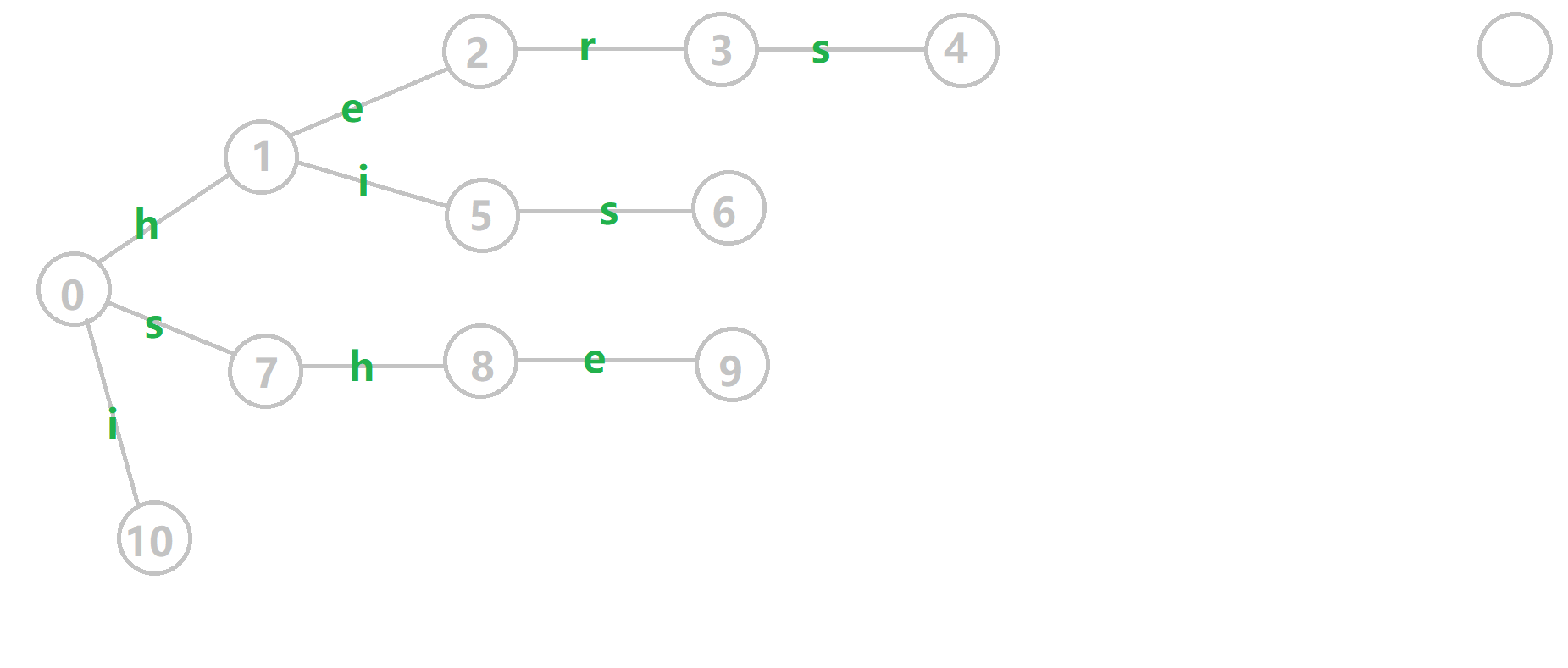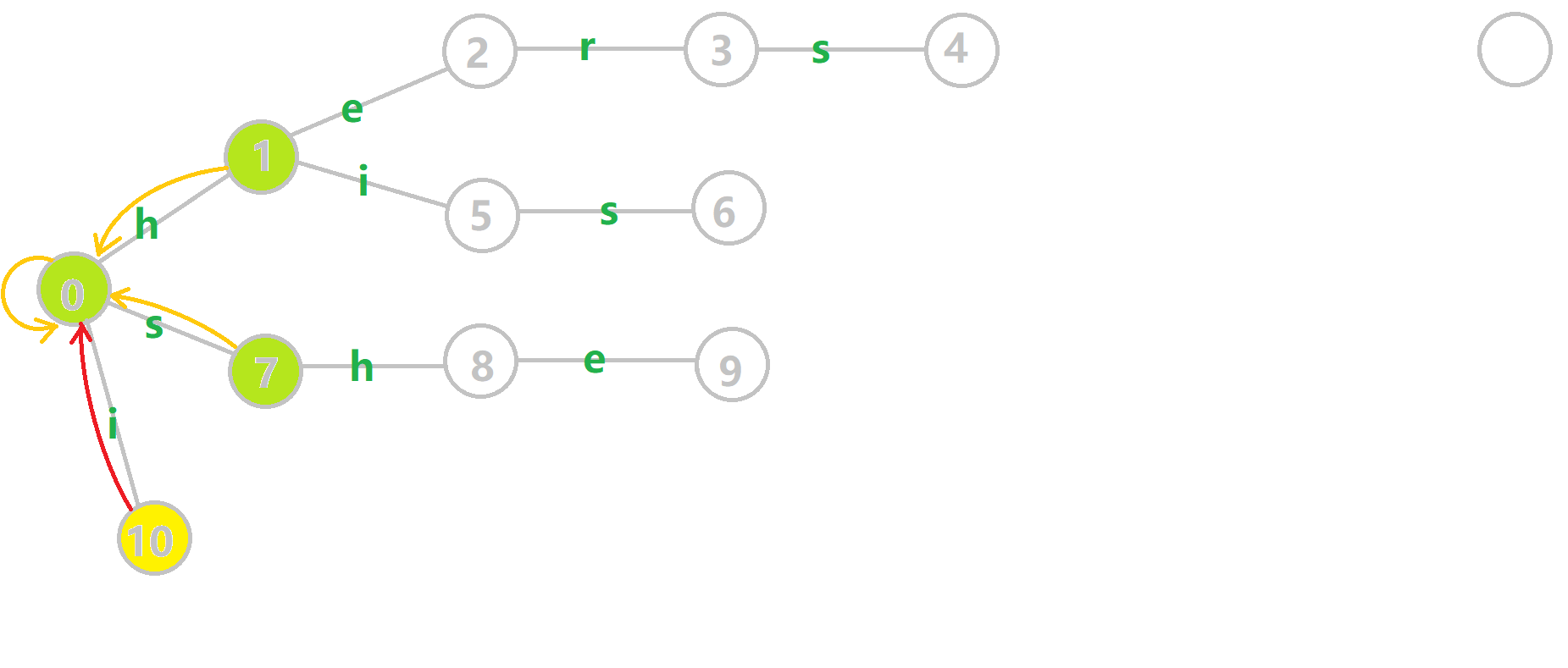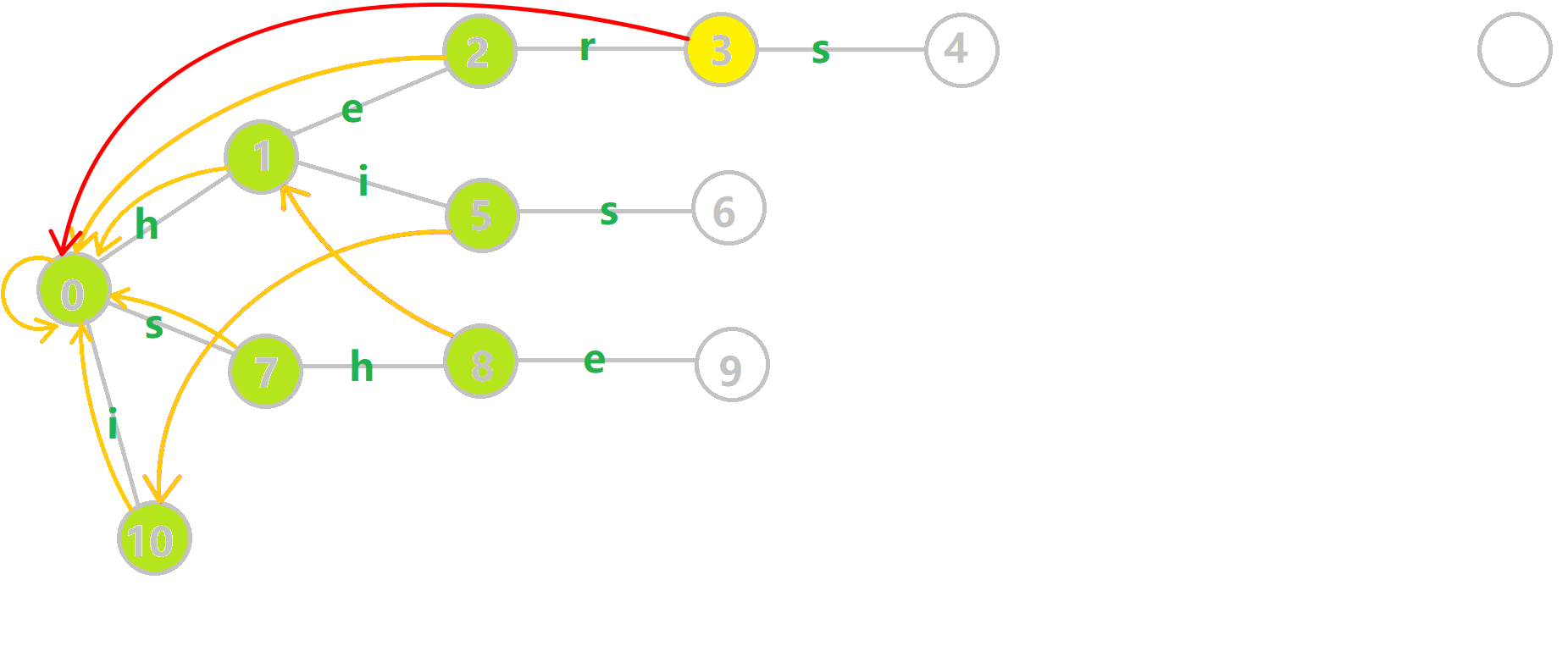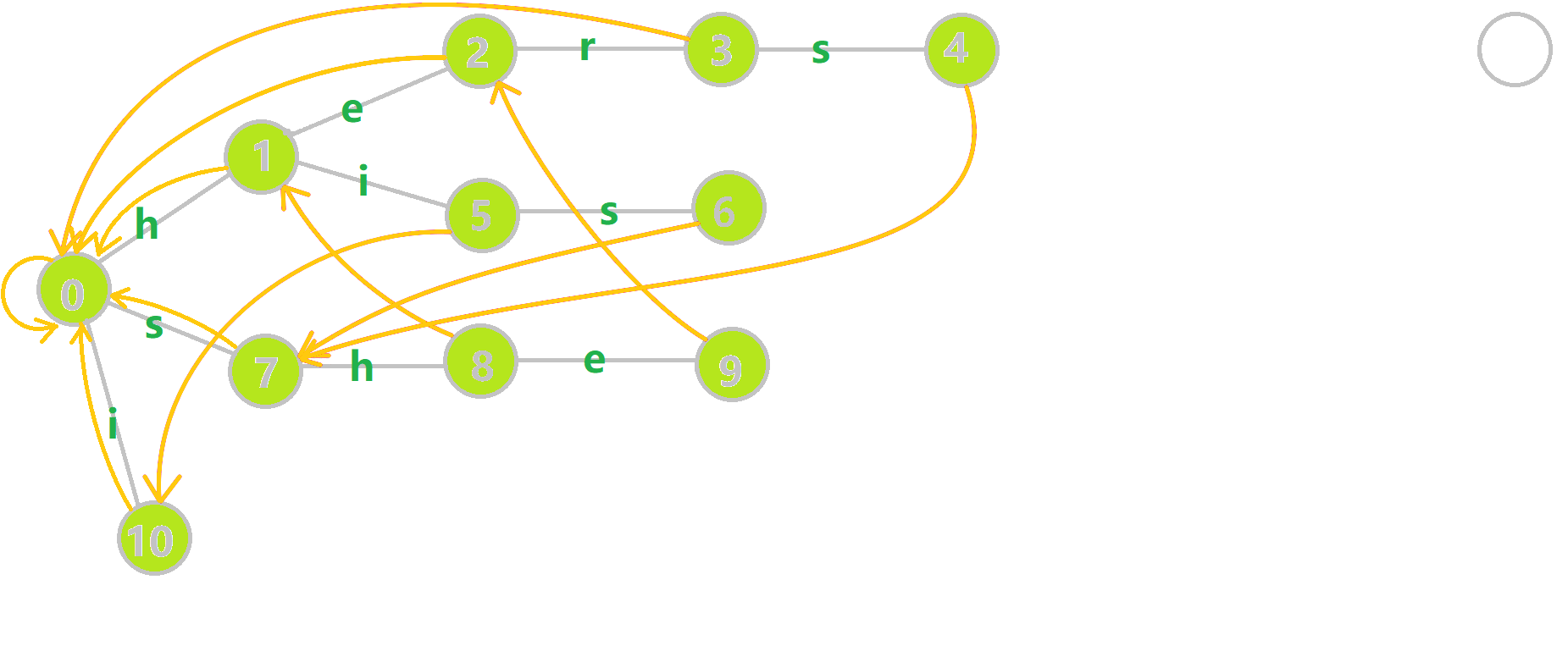
~~这个图恕我直言真的有点快,建议截下来一张一张看喵。~~
这个 $\mathrm{Fail}$ 指针的求法正是前面所写的一样,可以自己再画图模拟下喵。
----------------
## 7.2.实现
这个实现,就非常巧妙,他并不是用上面的方法实现的,而是一个更优秀的方法。
首先放个代码:
```cpp
inline void build()
{
queue<int>q;
for(int i=0;i<26;i++) if(t[0].v[i]) t[t[0].v[i]].nxt=0,q.push(t[0].v[i]);
while(!q.empty())
{
int u=q.front();q.pop();
for(int i=0;i<26;i++)
if(t[u].v[i]) t[t[u].v[i]].nxt=t[t[u].nxt].v[i],q.push(t[u].v[i]);
else t[u].v[i]=t[t[u].nxt].v[i];
}
}
```
这个时候我们发现在构建 $\mathrm{Fail}$ 指针的时候根本就没有循环往上跳,而是单独一次的指向。
`if` 引导的这一句显然没有疑问,唯一的疑问就是 `else` 这一句为什么可以直接指向。
其实原因也很简单,因为对于当前节点 $u$,不存在 $\delta(u,i)$ 的话,到时候调用到 $\delta(u,i)$ 的时候还是要跳往 $\mathrm{Fail}$ 指针尝试。
还不如直接把他指向 $\delta(\mathrm{Fail}_u,i)$ 。
而且这样操作的话相当于是并查集的路径压缩,每一次指向指向的就是之前那种方法 `while` 循环最后跳到的 $\mathrm{Fail}$。
非常巧妙的方法,如果不理解的话建议再自己对着代码画图看看。
其他建树查询就和 $\mathrm{Trie}$ 一样了,不再赘述。
$\LARGE{练习题}
P3808 AC 自动机(简单版)
附上 std。
P3796 AC 自动机(简单版 II)
附上究极无敌远古抽象马蜂 std。
还有个双倍经验喵:Dominating Patterns
P5357 【模板】AC 自动机
这个题要略微优化一二。
附上 std。
P3121 [USACO15FEB] Censoring G
纯板子。
7.3.应用
有关 $\mathrm{Fail}$ 树上套 $\mathrm{DS}$ 维护再加 $\mathrm{dp}$ 的题便是其一大特点。
-------------
### 7.3.1.[P3966 [TJOI2013] 单词](https://www.luogu.com.cn/problem/P3966) $\mathrm{Fail}$ 树板题
简要题意:
> - 给定 $n$ 个字符串,代表一篇文章中的单词。
> - 询问每个单词在文章里出现了多少次。
> - $n\le200,|s|\le10^6$。
什么是 $\mathrm{Fail}$ 树呢?
$\mathrm{Fail}$ 树,就是把 $\mathrm{ACAM}$ 中每个状态以他对应的 $\mathrm{Fail}$ 指针的状态作为父亲相连建出的树。
(注意这里建树连的边是反向的,因为要从根节点开始遍历方便。)
那这个 $\mathrm{Fail}$ 树他有什么性质呢?
显然的是对于一个点 $u$,若点 $v$ 在 $u$ 的子树里,那么 $u$ 点对应的状态是 $v$ 点对应的状态的子串。
这个性质还是非常显然的,因为对于点 $u$ 这个状态,点 $\mathrm{Fail}_u$ 对应的状态是点 $u$ 这个状态的后缀。
所以反向连边后就有了上面的这个性质。(如果还不懂的话可以画个图看看。)
那这道题怎么解决呢?
因为文本串就是模式串,所以直接就变成了一个子树加的问题。
~~那这个时候考虑 DS 维护。~~
哪里需要 DS 啊,甚至 $\mathrm{Fail}$ 树都不用真的建出来。
直接枚举下一路给 $\mathrm{Fail}$ 加上当前点的点权就行了。
因为 $\mathrm{Fail}$ 的点的编号肯定小于当前点,所以倒序枚举加上来即可。
附上 [std](https://www.luogu.com.cn/paste/d564a939)。
----------------------
### 7.3.2.[P4052 [JSOI2007] 文本生成器](https://www.luogu.com.cn/problem/P4052) $\mathrm{ACAM}$ 上 $\mathrm{dp}
简要题意:
- 给定 n 个只包含大写字母的字符串,随机生成一个长度为 m 的只包含大写字母的字符串,若其中含有前面给出的字符串,则是可以读懂的。
- 问可以读懂的字符串一共有多少个,答案对 10007 取模。
-
首先发现题目条件里是含有就可以算读懂,如果直接考虑做的话还要去重非常麻烦。
所以正难则反,考虑容斥,用总个数减去读不懂的个数。
总个数显然就是 26^m。
考虑如何求读不懂的个数。
首先对所有串建出 \mathrm{ACAM},接着考虑设计个 \mathrm{dp} 转移:
我们肯定要保证转移过来这个状态是读不懂的,但是如果 $j$ 这个串他读不懂,他的 $\mathrm{Fail}_j$ 能读懂怎么办。
比如输入的串为 `ssyxqwq`,`syxqw`。
我们目前的 $j$ 匹配上的状态是 `ssyxqw`,显然的是这个状态他是能读懂的。
所以我们考虑每个点的状态是否能读懂为 `mp[j]|=mp[fail[j]]`。
其中 $mp$ 数组的初值为这个点是否为一个串的结尾。
那这样的话如果 $mp_j=0$ 的话,$j$ 点这个状态就是肯定读不懂的了,大力转移即可。
附上封装 $\mathrm{ACAM}$ 板子前的 [std](https://www.luogu.com.cn/paste/vozp6nzy)。
$\LARGE{练习题}
P3041 [USACO12JAN] Video Game G
比较简单的 \mathrm{ACAM} 上 \mathrm{dp}。
P3311 [SDOI2014] 数数
比较烦的 \mathrm{ACAM} 上 \mathrm{dp},注意细节。
附上 std。
You Are Given Some Strings...
一个小思路转化+\mathrm{dp}。
附上 std。
P2292 [HNOI2004] L 语言
正解应该是状压 \mathrm{dp},但是懒癌的我写的是乱搞优化 \mathrm{dp}。
附上 std。
P4045 [JSOI2009] 密码 和 Password Suspects
双倍经验,都在题解区里了。
Digits of Number Pi
有一定难度,但应该没有 $3200$,详细讲解可以见 [CF585F 解题报告](https://www.luogu.com.cn/article/sqzwqs8m)。
-------------------
### 7.3.3.[P2444 [POI2000] 病毒](https://www.luogu.com.cn/problem/P2444) $\mathrm{ACAM}$+$\mathrm{dfs}$ 找环
简要题意:
> - 给定 $n$ 个 $0/1$ 串,问能否构造一个无限长的 $0/1$ 串不包含任何一个给出的 $0/1$ 串。
> - $n\le2000,\sum\limits_{i=1}^n|s_i|\le30000$。
这个题,可以加深对于 $\mathrm{ACAM}$ 的理解。
首先考虑把 $\mathrm{ACAM}$ 上面的边都看做单向边,$\mathrm{Fail}$ 指针也看做单向边。
那么显然是,如果能找到个环,环上所有点对应的状态都不是危险状态就是可行的。
接着来考虑一个状态什么时候为危险状态。
像上题一样,分为两种可能:
1. 他表示的状态就是一个危险的字符串。
2. 他的 $\mathrm{Fail}$ 指针指向的状态为危险状态。
那在构建 $\mathrm{Fail}$ 指针的时候直接给这个东西处理了。
接着在 $\mathrm{ACAM}$ 这张图上跑 $\mathrm{dfs}$ 找环即可。
附上 [std](https://www.luogu.com.cn/paste/7nkyvjci)。
------------
### 7.3.4.[P2414 [NOI2011] 阿狸的打字机](https://www.luogu.com.cn/problem/P2414) $\mathrm{Fail}$ 树+$\mathrm{BIT}
简要题意:
- 给定一个长度为 n 的包含小写字母和 B,P,的字符串 s。
- 最开始字符串 t 为空。
-
-
-
- 有 q 次询问,每次询问给出 x,y 表示询问第 x 次打印的 t 在第 y 次打印的 t 里出现几次。
-
多模匹配计数问题,首先考虑 \mathrm{ACAM}。
那 \mathrm{ACAM} 怎么做呢?
这个题的串串里还有奇怪的操作,插入貌似不能用以前那种。
没事,题面怎么写,我们插入函数就怎么写:
inline void insert(char s[],int n)
{
int u=0;
for(int i=1;i<=n;i++)
{
if(s[i]=='P') Q[++cnt]=u;
else
if(s[i]=='B') u=t[u].f;
else
{
int v=s[i]-'a';
if(!t[u].v[v]) t[u].v[v]=++tot,t[tot].f=u;
u=t[u].v[v];
}
t[u].ed=1;
}
}
对于每一次输出的字符串,再给他的状态对应的点存储下来。
每次往下加字符就记录下 fa 方便回退操作。
然后再和正常的一样给末尾点打上结尾标记。
现在,我们有了一只 \mathrm{ACAM}。
接着来考虑怎么查询。
查询操作,相当于查询 q_y 这个点的状态的所有的子串在 x 次打印中的串中的出现次数之和。
考虑把在第 x 打印的串的子串节点权值全部加上。
那么变成了查询 q_y 这个点对应状态的子串节点权值和。
发现存在一次打印的串被查询多次而有几次打印的串却没被查询过的情况。
考虑把询问离线下来,对于每一个 y 进行回答。
接着发现子串是难以突破的关键。
想到什么?
前面提到过在 $\mathrm{Fail}$ 树中,若 $v$ 在 $u$ 的子树里,则 $u$ 是 $v$ 的子串。
利用这个性质,对于 $x,y$ 的查询,就变成了加上 $y$ 的贡献,查询 $x$ 的子树和。
那怎么维护单点加减,子树求和呢?
~~树链剖分!~~ 其实不然,$\mathrm{BIT}$ 足以。
附上 [std](https://www.luogu.com.cn/paste/zyjf3baf)。
$\LARGE{练习题}
e-Government
和上面这题基本没区别,纯板子,用于巩固提升。
std。
Indie Album
这题思维有一定难度。
考虑不对 s 建 \mathrm{ACAM},不然就要动态更改结构。
所以我们考虑对 t 建 \mathrm{ACAM},剩下部分就和上面没区别了。
std。
[CERC2018] The ABCD Murderer
简单 \mathrm{DS+dp},代码和思路可以见题解。
7.3.5.Death DBMS \mathrm{ACAM}+树剖!
简要题意:
- 给出 n,m,然后给出 n 个字符串,每个字符串都有一个权值,最初权值都为 0。
- 然后有 m 个操作,操作有两种类型:
- 将第 i 个字符串的权值修改为 x。
- 给出一个字符串 t,求所有是 t 的子串的字符串的权值的最大值。
-
乍一看好像和前面那题没有区别,因为也是一个查询子串的权值问题。
所以应该也要建出 \mathrm{Fail} 树在上面跑 \mathrm{BIT}?
询问的是最大值!
显然的是 $1$ 操作就是单点修改。
而 $2$ 操作呢?
就是查询当前点到 $0$ 节点路径上的最大点权。
(如果不理解的话可以画图看看。)
接着因为询问的串 $q$ 的每个子串都是可行的,所以我们要在 $\mathrm{ACAM}$ 上跑这个串的同时对于每个跑到的点进行一次查询。
显然这种路径问题需要**树剖**维护,所以大力剖即可。
附上**套了一堆板子的抽象** [std](https://www.luogu.com.cn/paste/swxvzuhl)。
$\LARGE{练习题}
GRE - GRE Words
**注意这题有点卡常,常数不要太大。**
附上 [std](https://www.luogu.com.cn/paste/k14sfthh)。
~~还有他的 UVA 双倍经验黑 [GRE Words](https://www.luogu.com.cn/problem/UVA1502)。~~
~~别问为什么画了条删除线,问就是这题太**了,用前面的那个代码过不去。~~
-----------------
### 7.3.6.[P2336 [SCOI2012] 喵星球上的点名](https://www.luogu.com.cn/problem/P2336) 思路转化+$\mathrm{Fail}$ 树+$\mathrm{BIT}
简要题意:
- 给定 2\times n 个序列,其中第 i 个和第 i+1 个的编号都是 \frac{i}{2}(i\bmod2\equiv0) 。
- 再给定 q 个序列,询问这个序列是前面多少个不同编号的序列的子串。
- 最后在输出每个编号的序列包含了多少个不同的询问序列。
- 也就是对于一个编号,他的两个序列得到的答案是或的关系。
-
这个题,只能说,泰裤辣!
Warning:请确保自己已经深刻了解 \mathrm{Fail} 树的意义。
首先这种序列但又是子串的问题,考虑 \mathrm{ACAM}。
但是 \mathrm{ACAM} 实质是一只字典图,这么大的值域不得炸光了?
所以考虑使用 map 来代替原本建树里的 v 数组。
接着发现每个编号他有两个序列,到时候统计还要去重,不得烦死。
所以考虑直接把这两个序列拼接起来,可以在中间插入一个 -1 来间隔开。
接着再考虑把询问序列也给扔 \mathrm{ACAM} 里方便后续操作。
接着这个问题又变成了统计出现过的子串个数,想到和上面类似的方法:
\mathrm{Fail} 树+\mathrm{BIT}!
但这样是有点问题的,我们先按照这个思路给题目转化过来看看:
-
对于第一问,就是对每个编号的序列的点覆盖到 0 节点然后取个并集的修改。
查询即为单点查询。
-
而对于第二问,就是询问序列状态单点修改。
查询即为对每个编号从 0 到结尾链查询。
这玩意好做吗?
显然不好做,覆盖是什么神仙玩意啊。
所以来考虑怎么转化题意。
首先对于第一问,可以转化为树上单点修改,子树查询。
但是显然的是这样也会有重复部分,所以要去重。
那怎么去重呢?
我们发现,开始重复的位置就是两个修改了的点的 \mathrm{LCA} 的位置,所以只需要给他们的 \mathrm{LCA} 这里点权 -1 就行了。
但这样就做完了吗?
因为修改的点有很多,所以很多地方都会重,但是我们去重肯定要去掉一个最近的 \mathrm{LCA}。
也就是,题意转化了求在树上的 k 个点的最小连通子图会经过的 \mathrm{LCA}。
这玩意有一道题目:P3320 [SDOI2015] 寻宝游戏和经验Archaeology。
首先我们能知道的一个很显然的结论,就是这样求出来的 \mathrm{LCA} 个数不会超过 k-1 个。
因为一个点向上走到一个 \mathrm{LCA} 至少能再向下走到另外一个点。
这里先给出结论:把这些点按照 \mathrm{dfn} 序排序后,相邻的两个点取 \mathrm{LCA} 即为最近 \mathrm{LCA}。
接着考虑证明:
首先考虑排序的步骤。
我们把每个点的所有儿子按照 \mathrm{dfn} 序排序,使得在主观意义上小的 \mathrm{dfn} 序的点在大的左边。
比如这张图(点的编号表示 \mathrm{dfn} 序):
假设我取出的带标号的点为 a_i,并且只考虑这个点与 a_{i\sim n} 的贡献(a_i 与前面贡献已经在 a_{1\sim i-1} 的时候算完了)。
考虑下这个 \mathrm{LCA} 要满足的条件是能走到 a_{i+1\sim n} 中的任意一个点。
显然的是这个 \mathrm{LCA} 肯定在 1\rightarrow a_i 的路径上,且由定义得要与 a_i 最近,也就是 a_i 往上跳最少的步数。
考虑每个点他对应子树的 \mathrm{dfn} 序是一个区间,设点 i 对应的区间右端点为 ed_i,那么显然的是 i 的 \mathrm{dfn} 序区间是 dfn_i\sim ed_i。
因为我们只要求 a_{i+1\sim n} 的贡献,而他们的 \mathrm{dfn} 序又是单增的,所以只需要考虑 ed_i 即可。
显然当 a_i 这个点不断往上跳时,其 ed 为单调不减(因为父亲节点他的 ed 是 \max\{ed_{son}\} )。
而 a_i 跳到的点 u 能到达 v 的充分条件是 dfn_v\le ed_u(由前面的排序得 dfn_{a_i}<dfn_v)。
所以 dep_{\mathrm{LCA}(a_i,a_{i+2})}\le dep_{\mathrm{LCA}(a_i,a_{i+1})}。
也就是 \mathrm{LCA}(a_i,a_{i+1}) 即为最近的 \mathrm{LCA}。
所以这个结论就成立了。
那么回到正题,这里我们只需要对于每个编号的序列的所有状态的点一路修改上去,然后去重就行了。
查询即为前面所说的子树查询。
//tt为 BIT,id[i]为编号 i 对应的状态的结尾点,q[i]为第 i 次询问对应的状态结尾点
memset(tt.c,0,sizeof tt.c);
for(int i=1;i<=n;i++)
{
//修改
int u=id[i],tot=0;
while(u) a[++tot]=u,tt.modify(dfn[u],1),u=ac.t[u].fa;
//去重
sort(a+1,a+1+tot,cmp);
for(int j=1;j<tot;j++) tt.modify(dfn[LCA(a[j],a[j+1])],-1);
}//查询
for(int i=1,u;i<=m;i++) u=q[i],print(tt.query(dfn[u],dfn[u]+si[u]-1)),puts("");
而对于第二问,类似的,只不过是修改查询对调:
memset(tt.c,0,sizeof tt.c);
for(int i=1,u;i<=m;i++) u=q[i],tt.mdf(dfn[u],dfn[u]+si[u]-1,1);
for(int i=1;i<=n;i++)
{
int u=id[i],tot=0,res=0;
while(u) a[++tot]=u,res+=tt.query(dfn[u]),u=ac.t[u].fa;
sort(a+1,a+1+tot,cmp);for(int j=1;j<tot;j++) res-=tt.query(dfn[LCA(a[j],a[j+1])]);
print(res);putchar(' ');
}
最后,附上 std。
\LARGE{练习题}
这一块的练习题主要特点是难于上面那块。
Mike and Friends
这题好像没那么难?感觉 2800 有点高了。
如果写过 \mathrm{P4211} 的话应该不难想。
std。
P5840 [COCI2015] Divljak
std。
JZPGYZ - Sevenk Love Oimaster
std。
这两题,是类双倍经验,有一定难度,可以思考一二。
7.3.7.GEN - Text Generator \mathrm{ACAM}+矩阵优化~\mathrm{dp}
简要题意:
- 给定 n 个字符串,求包含这 n 个字符串中的任意一个的长度为 l 的字符串有多少种。
-
第一眼看到这题,不就是 6.3.2.P4052 [JSOI2007] 文本生成器 吗?
仔细一看,不太对劲的样子,这个 l\le10^6 早把文本生成器的做法干爆了。
(如果忘记文本生成器怎么做了,可以去前面看看喵。)
下面重点来讲下这个玩意怎么优化。
因为我们的 \mathrm{dp} 的转移是一步步推过来的,那么 dp_l 就是从 dp_0 转移 l 步得到的。
也就是相当于走了 l 步。
也就是在 \mathrm{ACAM} 上走了 l 步。
因为 \mathrm{ACAM} 上的点不是很多,所以点直接两两走的方案数可以用邻接矩阵存起来。
那么,走 1 步的矩阵是不是就为初始矩阵?
如果我们把走 1 步的矩阵相乘,是不是得到了走 2 步的矩阵?
再次把走 2 步的矩阵相乘,是不是得到了走 4 步的矩阵?
那是不是就可以矩阵快速幂优化走 l 步这个过程?
因为从初始状态开始,最后走到哪个状态结尾都有可能,所以要取矩阵的第一行答案相加。
还有这题略卡常,无用的状态要直接扔掉。
std。
\LARGE{练习题}
Legen...
这个题更有难度一点,需要一定的思维转化。
详情可以见 CF696D 解题报告。
7.3.8.String Set Queries 可持久化 \mathrm{ACAM}
非常好玩的题。
简要题意:
查询所有字符串在给定字符串中的出现次数这个操作,考虑用 \mathrm{ACAM} 来解决。
接着考虑处理其他两种操作,因为删不太好弄,所以考虑把他变成减去其出现次数。
实现上也就是将删的字符串插入另一个 \mathrm{ACAM} 中,然后查询时答案减去这个 \mathrm{ACAM} 中查询出的答案。
接着考虑本题的难点:强制在线。
这点就让 \mathrm{ACAM} 非常难办了,总不可能每加一个字符串就重构一遍 \mathrm{Fail} 指针吧。
那么我们就要让重构 \mathrm{Fail} 指针的次数最小,能不重构就不重构。
这样会想到什么呢?
二进制分组!
具体的,类似于 2048,把字符串按照二进制分组后,对于每一块建一个 \mathrm{ACAM},碰到相同大小的块就合并暴力重构。
再具体些,比如大小为 4 的块中,就有 4 个字符串,并对他建了个 \mathrm{ACAM}。
如果再来了个大小为 4 的块,就将他们合并为大小为 8 的块,暴力重构 \mathrm{Fail} 指针。
因为最后合并出来的最大块也仅为 n,所以合并步骤不会超过 \log n 次,复杂度仅多一只 \log 完成在线。
最后查询的时候遍历每个块的 \mathrm{ACAM} 算答案就行了。
附上 std。
\LARGE{练习题}
ADAJOBS
这个题可以离线做但是也可以用在线做法写。
std。
7.3.9.Duff is Mad/P7582 「RdOI R2」风雨(rain) 根号相关的 \mathrm{ACAM}
按顺序来看两个题好了,先是 Duff is Mad。
简要题意:
别把题面看错了,注意是区间串在单串中的出现次数。
这个就不太好做了,如果是单串在区间中的出现次数话就非常好处理。
考虑怎么暴力用 \mathrm{ACAM} 处理。
先建 \mathrm{Fail} 树,对于区间 [l,r] 的串全部都子树加。
查询直接暴力跳单串的每一个点,把权值加上就行了。
这样的话我们的复杂度是 O(n^2\log n) 的,因为字符串长度和 n 同阶。
不难发现,因为是加和,所以区间 [l,r] 可以被拆为 [1,r]-[1,l-1]。
但因为我们的单串是暴力跳的,所以复杂度还是高居不下。
那这个时候还能怎么处理呢?
考虑把子树加链查改掉,改成链加子树查。
前者是对于区间的每个串子树加,然后单点查询问串的每个位置。
后者是对于询问串整个链加,然后对于区间的每个串查询权值即可。
看起来这两种方法是没有区别的,但是仔细分析我们就会发现,这两种方法的复杂度分别是:
$O(nk\log n+m)$,其中 $k$ 表示串的个数,而 $m$ 的定义同上。
观察到如果我们设定一个阈值 $lim$,长度大于 $lim$ 的用下面那个方法,长度小于 $lim$ 的用上面那种方法。
那么复杂度就分别是 $O(nlim\log n)$,$O(n\frac{n}{lim}\log n+lim)$。
显然当 $lim=\sqrt{n}$ 时复杂度最优,也就是根号分治平衡复杂度。
然后按照思路直接实现就行了,可能还有点实现难度。
[std](https://www.luogu.com.cn/paste/hu75prdq) 喵。
接着是 [P7582 「RdOI R2」风雨(rain)](https://www.luogu.com.cn/problem/P7582)。
~~同样是黑我感觉这题就比上题难很多。~~
简要题意:
> - 给定 $n$ 个字符串 $s_i$,第 $i$ 个字符串的权值为 $a_i$。
> - 有 $m$ 次操作,分为下面三种:
> 1. 给定区间 $[l,r]$ 和 $x$,给 $a_{l\sim r}$ 区间加 $x$。
> 2. 给定区间 $[l,r]$ 和 $x$,给 $a_{l\sim r}$ 赋值为 $x$。
> 3. 给定区间 $[l,r]$ 和 $x$,定义 $cnt_i$ 为 $s_i$ 在 $s_x$ 中的出现次数,询问 $\sum\limits_{i=l}^r cnt_i\cdot a_i$。
> - $n,m\le 3\times10^4,\sum\limits_{i=1}^n|s_i|\le2\times 10^5$,字符集只有 $a,b,c$,$2s$ 时限。
首先看到题意查询 $s_{l\sim r}$ 在 $S$ 中的出现次数,首先想到了 [CF587F](https://www.luogu.com.cn/problem/CF587F)。
尝试类似的根号分治方法?
接着被这题的字符串带权值且带修改创飞了。
接着发现这题比较特殊的一点,字符集只有 $a,b,c$ 且 $n$ 范围较小,甚至还给了 $2s$。
考虑下最基础的 $\mathrm{ACAM}$ 是怎么统计出现次数的:
- 把模式串插入 $\mathrm{ACAM}$ 里,构建 $\mathrm{Fail}$ 树后对着每个模式串末尾节点子树加。
- 接着对于查询串扔到 $\mathrm{ACAM}$ 上跑,加上每个点的权值。
这个方法考虑树状数组维护即可。
不难发现这个方法在字符串带权值的时候还是适用的,把子树加的值从 $1$ 改为其权值即可。
接着考虑怎么给这个玩意带修改。
子树加的东西,要是修改就只能单个改,做不了一点。
所以考虑万能的分块(结合上面较小的数据范围也可以推出来复杂度里大概会带个根号了)。
我们考虑对 $n$ 个字符串分块为 $\sqrt{n}$ 个长度为 $\sqrt{n}$ 的字符串,对于每块字符串建一个 $\mathrm{ACAM}$。
那么一次修改/覆盖操作就被我们拆分为了如何处理整块和散块。
基础分块方法,对于散块直接在树状数组上每个点子树修改,整块打标记即可。
接着考虑怎么查询:
- 对于散块,直接大力上 $\mathrm{KMP}$ 查询。
- 对于整块,直接把字符串扔到整块的 $\mathrm{ACAM}$ 上跑然后一路加单点权值。
~~貌似也不是 too hard?~~
然后我就把 $tag$ 和 $lz$ 数组写反挂到 $49$ 了。
**P.S.:散块跑 KMP 前先判断长度,不然复杂度会寄。**
代码可以见[题解](https://www.luogu.com.cn/article/m3mdcmvi)喵。
------------------------
### 7.3.10.[P8571 [JRKSJ R6] Dedicatus545](https://www.luogu.com.cn/problem/P8571) $\mathrm{ACAM}$+虚树
简要题意:
> - 给定 $n$ 个字符串 $s_{1 \dots n}$。
> - 定义 $w(i,j)$ 表示 $s_i$ 在 $s_j$ 中的出现次数。
> - $q$ 次询问 $\max\limits_{i=l}^r w(i,k)$。
> - $n,q\le10^5,\sum\limits_{i=1}^n |s_i| \le 5\times10^5$。
下文中我们用 $k$ 代表字符串总长,也就是 $k$ 的范围是 $5\times10^5$,$n,m$ 的范围是 $10^5$。
题面都和 [CF587F Duff is Mad](https://www.luogu.com.cn/problem/CF587F) 差不多了,肯定是类似的思路先尝试想想。
考虑直接套做法,上来一个根号分治。
上一题里我们考虑根号分治后差分,把复杂度降下去,但是这个是 $\max$ 并不支持差分。
不管了还是尝试根号分治,设块长为 $B$,我们先考虑比较简单的长度 $>B$ 的。
还是一样的做法,对询问串整个链加,然后对于区间 $[l,r]$ 子树查。
因为不能差分,所以我们要换一个东西来查询区间的最大值。
可以考虑用线段树/ST 表。
但是分析下复杂度就会发现,如果用 ST 表,要对 $\frac{k}{B}$ 个串进行 $n\log n$ 的处理,如果不用 $O(n)$ 预处理的 ST 表是过不了的。
而查询次数顶满也就 $m$,所以肯定是把 $\log$ 放在询问上更合理。
然后对于子树查询,同理,因为我们要对 $\frac{k}{B}$ 个串都进行构造,所以复杂度要压在 $O(k)$ 处理出 $k$ 个点的子树值。
反正是静态的,直接前缀和预处理出来就行了。
至此第一部分完成了,总的复杂度 $O(n\frac{k}{B}+m\log n)$。
然后来考虑第二部分。
显然的是,在这个部分我们不能枚举区间 $[l,r]$,不然就会炸飞。
但是好处就是这个部分的点数只有 $B$。
考虑下,因为最多只有 $B$ 的长度,所以最大的答案就是 $B$。
把这个意义搞到 Fail 树上再理解一下。
那就是,我们对查询串链加后,子树查的值只会有 $B$ 种。
因为他有用的点就最多只有 $2B$ 个,因为每两个点召唤出来一个新点。
反正答案这么少,我们考虑找到每一个答案改变的断点。
也就是对于 $fa_i,i$,如果二者答案一样,我们就不要 $fa_i$。
不难发现,其实这些断点,组成的树,就是这 $B$ 个点的虚树。
因为你的答案只有在一个新的点和之前点的 LCA 处,会把二者的答案合并从而改变答案。
所以我们对于每个询问串,建一个属于他的虚树。
那对于虚树上的每个点 $i$,处理出 $s_i$,那么只要有一个 $[l,r]$ 的字符串的结尾点子树中有 $i$,答案就能取到 $s_i$。
我们不要考虑 $[l,r]$,还是考虑 $i$,就是根节点到 $i$ 的路径上有有 $[l,r]$ 字符串结尾点。
接着问题就变成,怎么做链查询是否存在编号 $[l,r]$ 的点了。
考虑扫描线,把所有区间 $[l,r]$ 的询问都扔到 $r$ 上去。
扫描线了,所以是单调的,我们只要一直覆盖就行了。
查询也直接查询即可,如果查询出来的最大值是 $\ge l$,就说明能取到。
因为我们现在放入的数只有 $[1,r]$,所以找到 $\ge l$ 的就是能取到。
考虑使用分块,这里显然是把块长取到 $\sqrt{k}$ 优,可以做到整块散块复杂度不变。
因为分块是 $O(\sqrt{k}),O(1)$ 的,所以我们的复杂度是 $O(k\log{k}+n\sqrt{k}+mB)$。
第一部分是虚树的复杂度,第二部分是分块修改,第三部分是查询询问。
所以总的复杂度就是 $O(n\frac{k}{B}+m\log n+k\log{k}+n\sqrt{k}+mB)$,所以最优块长应该是取 $\sqrt{\frac{nk}{m}}$。
即是 $O(m\log n+k\log{k}+n\sqrt{k}+\sqrt{nkm})$。
但是因为虚树和线段树的常数问题,实际写的话写个 $O(\sqrt{2k})$ 就能跑的飞快。
代码可以见[题解](https://www.luogu.com.cn/article/aucjr8p9)了。
$\LARGE{练习题}
P9935 [NFLSPC #6] 啊,忘记了。 折磨题,还在补。
7.4.后记
目前就先告一段落了,后面的几道结合虚树或是其他的逆天 $\mathrm{ACAM}$ 题,有时间再来补吧。
实际使用的时候 $\mathrm{ACAM}$ 也不能算是一个思维的难点,推出 $\mathrm{ACAM}$ 还是很顺利的。
重点就在其上结合的 $\mathrm{dp}$ 或是其他 $\mathrm{DS}$ 了。
但他也有很多维护不了的东西,这些就得看后面的后缀系列了。
# 8.$\mathrm{SA}
注意,请区分这里的 \mathrm{SA} 和模拟退火那个 \mathrm{SA}。
此处的 \mathrm{SA} 指的是 \mathrm{Suffix~Array},即为后缀数组,用于处理字符串的一系列问题。
用途较为广泛,可以处理 \mathrm{ACAM} 不能处理的本质不同子串等问题。
8.1.定义
首先后缀的概念就非常清楚了,取长度为 n 的字符串 s 的 s_{i\sim n} 即为 s 的后缀。
而 sa_i 便是将 s 的所有后缀按照字典序排序后,排名为 i 的后缀以 sa_i 为头。
这点还是比较好理解的,$rk$ 表示 $rank$ 表示的就是排名嘛,另一个也就是映射了。
在这里也涉及了一个概念:**将 $s$ 的所有后缀按照字典序排序**。
具体的原因后面再说,这里记住就行。
--------------
## 8.2.实现
既然已经知道什么是 $\mathrm{SA}$ 了,接着来考虑怎么求他。
首先考虑最朴素的方法,把 $s$ 的所有后缀处理出来,然后直接大力排序。
复杂度大于 $O(n^2)$,实现难度较低,在此不再赘述。
接着来考虑怎么加速这个排序过程。
因为我们不能把整个后缀拿出来比较,所以考虑把后缀分为一部分一部分比较。
那怎么拆分这些后缀最优呢?
考虑倍增,把其变为长度为 $2^i$ 的字符串。
每次比较时,我们考虑把**原本无法比较出的**,长度为 $2^i$ 的字符串拼接上他后面的那一段再进行比较。
这样长度就变成了 $2^{i+1}$,但是如果还是暴力比较的话复杂度并无优化。
发现这样有什么**优点**?
显然的是这个长度为 $2^{i+1}$ 的字符串长度为 $2^i$ 的前后缀的**排名**都已经知道了。
把这两个**排名**拿出来,即为两个**关键字**。
我们排序的原则显然是优先比**第一个排名**大小,再比**第二个排名**大小。
那么,对于这个长度为 $2^{i+1}$ 的字符串的排序,就相当于是**双关键字排序**。
考虑使用快速排序完成每次双关键字排序,复杂度为 $O(n\log^2 n)$。
但是这样显然很劣,例如[模板题](https://www.luogu.com.cn/problem/P3809)中,用 $\mathrm{Hash}$ 做的复杂度也为 $O(n\log^2 n)$,写了半天还不如简单易懂的 $\mathrm{Hash}$。
再次考虑优化。
不难发现瓶颈在排序上,只要有方法去掉排序上的一只 $\log$,复杂度就可以来到优秀的单 $\log$。
因为我们的排序是**双关键字排序**,关键字不多且值域不大,可以怎么优化呢?
**基数排序!**
因为**第一关键字**也就是长度为 $2^i$ 的后缀排序,在上一次已经处理出来了,所以只对**第二关键字**进行**基数排序**即可。
这样复杂度就成功来到了优秀的 $O(n\log n)$。
下面借用下 OI-Wiki 中的图(笔者真的找不到什么好的画图软件,如果有推荐的话欢迎踹我重画):

刚刚所说的**双关键字排序**在这张图里便非常显然了,每次把他后面那段的 $rk$ 也拿上来排序即可。
代码也挺好写的,即为:
```cpp
inline void get_SA(int n,int sa[],int rk[],int old[],char s[])
{
//c 为桶,用于基数排序;sa,rk,s 定义如上;old 用于储存 oldrk;m 为值域
for(int i=1;i<=n;i++) ++c[rk[i]=s[i]];
for(int i=2;i<=m;i++) c[i]+=c[i-1];
for(int i=n;i>=1;i--) sa[c[rk[i]]--]=i;
for(int k=1;k<=n;k<<=1)
{
int tot=0;
for(int i=n-k+1;i<=n;i++) old[++tot]=i;
for(int i=1;i<=n;i++) if (sa[i]>k) old[++tot]=sa[i]-k;
for(int i=1;i<=m;i++) c[i]=0;
for(int i=1;i<=n;i++) c[rk[i]]++;
for(int i=2;i<=m;i++) c[i]+=c[i-1];
for(int i=n;i>=1;--i) sa[c[rk[old[i]]]--]=old[i],old[i]=0;
swap(rk,old);rk[sa[1]]=1;tot=1;
for(int i=2;i<=n;i++) rk[sa[i]]=(old[sa[i]]==old[sa[i-1]]&&old[sa[i]+k]==old[sa[i-1]+k])?tot:++tot;
if(tot==n) break;m=tot;
}
}
```
~~其实还可以再优化的。~~
欸还真有优化的方法,名叫 $SA-IS$,可以把复杂度压到 $O(n)$。
但是 $SA-IS$ 还不是最优的,他的空间有点大,还有个空间只有其 $\frac{1}{3}$ 的算法:
**最优原地后缀排序算法!**
这两个算法因为笔者能力有限,暂且搁置,后续应该**也不会**补上。
----------
## 8.3.$\mathrm{SA}$ 与 $\mathrm{LCP}
要是 \mathrm{SA} 只能进行快速的后缀排序的话,那他的应用会被大大限制。
所以其与 \mathrm{LCP} 也有联系。
定义 height_i 表示 \mathrm{LCP}(sa_i,sa_{i-1})。
特殊的,对于 height_1,其值可视为 0。
既然定义了 height,接着就来考虑怎么快速求 height。
这里需要用到一个引理:height 引理。
其内容即为:height_{rk_i}\ge height_{rk_{i-1}}-1。
- 当 height_{rk_{i-1}}\le1 时:
- 根据定义 height_{rk_i}\ge0,上述式子显然成立。
- 当 height_{rk_{i-1}}>1 时:
- 不妨设 \mathrm{LCP}(sa_{rk_{i-1}},sa_{rk_{i-1}-1}) 为 s+Y,其中 s 为一个字符,Y 表示一个字符串,加号表示连接。
- 那么设 sa_{rk_{i-1}} 这个后缀为 s+Y+X;sa_{rk_{i-1}-1} 这个后缀为 s+Y+F,其中 X,F 表示两个不同的字符串。
- 那么,后缀 sa_{rk_i} 就可以表示为 Y+X,并且,存在后缀 Y+F(就是上面那两个字符串各剥掉第一位)。
- 显然的是后缀 sa_{rk_i-1} 被约束在了 Y+F 和 Y+X 中。
- 既然这个后缀在这中间,那么他也必然可以表示为 Y+? 的形式,其中 F\le?<X。
- 那么 \mathrm{LCP}(sa_{rk_i},sa_{rk_i-1}) 就至少为 |Y| 了,也就是 height_{rk_{i-1}}-1。
- 证毕!
具体的求 height 数组,根据这个引理暴力即可:
inline void get_height(int n,int h[],int rk[],char s[])
{
int k=0;
for(int i=1;i<=n;i++) rk[sa[i]]=i;
for(int i=1,j;i<=n;i++)
{
if(rk[i]==1) continue;if(k) k--;j=sa[rk[i]-1];
while(j+k<=n&&i+k<=n&&s[i+k]==s[j+k]) k++;
h[rk[i]]=k;
}
}
复杂度为严格 O(n),因为其中的 k 最多减 n 次,而加最多加到 n。
接着有一些有关于 height 数组的推论:
-
\mathrm{LCP}(sa_i,sa_j)=\min(height_{i+1\sim j}),i<j
这个结论挺显然的。
因为后缀是被排序过的,所以他的每位字符变大是从后往前单调不减的。
也就是,如果存在 i<k\le j 满足 height_k<height_{k-1},那么后缀 k 必然是在 height_k+1 这一位变大了一点。
那么显然的是后缀 sa_i 的前 height_k+1 位必然小于后缀 k 的 height_k+1 位小于等于后缀 sa_j 的 height_k+1 位。
因为后缀都是经过排序的,所以这个变换过程必然是单调的,也就是 \mathrm{LCP}(sa_i,sa_j)\le \min(height_{i+1\sim j}),i<j。
接着来证为什么能取等。
因为 height_{i+1\sim j}\ge \min(height_{i+1\sim j}),所以他前面至少有 \min(height_{i+1\sim j}) 位是相等的。
也就是能够取等,得证。
-
比较 s_{x\sim y} 和 s_{i\sim j} 大小:
分两种情况:
-
- $s_{x\sim y}<s_{i\sim j}$ 即为 $y-x+1<j-i+1$。
- 否则:
这个有点显然了,就不写严谨的证明了。
-
本质不同子串个数:
因为后缀满足开头的位置两两不相同,所以答案即为每个后缀的前缀去重。
考虑怎么样的情况才会重复,即为相同的前缀。
这不就 \mathrm{LCP} 的前缀吗,那么重复前缀的数量即为 \sum\limits^n_{i=1}height_i,拿全部子串数 \frac{n(n-1)}{2} 减下即可。
SUBST1 - New Distinct Substrings 例题喵。
std。
双倍经验。
略微扩展的板子。
比较有意思的相关题,题解。
其他相关就在后面题目中再说了。
8.4.应用
这里主要讲一些常见的 $trick$ 了。
-----------
### 8.4.1.[PHRASES](https://www.luogu.com.cn/problem/SP220) 最长不重叠出现子串
简要题意:
> - 给定 $n$ 个字符串 $s_{1\sim n}$,询问最长的在 $s_{1\sim n}$ 都不重叠的出现次数 $x\ge2$ 的字符串。
> - $n\le10,\sum|s|\le1.5\times10^4$。
直接做这个题还是太难了,因为要找到的串要在 $n$ 个串中都满足限制条件。
所以不妨先来考虑他的弱化版:[P2743 [USACO5.1] 乐曲主题Musical Themes](https://www.luogu.com.cn/problem/P2743)。
这题就是 $n=1$ 且对答案有些限制的弱化版。
首先根据其给出的定义,音符可能转音,但是转音是整体加减,所以 $\Delta$ 并不会有区别。
先考虑把字符串 $s_{1\sim n}$ 变为 $t_{1\sim n-1}$,其中 $t_i=s_{i+1}-s_i$。
那这样就处理掉了转音的问题,完全变成了上面那题的弱化版。
首先考虑使用 $\mathrm{SA}$ 来解决这个问题。
但是 $\mathrm{SA}$ 貌似并不方便做欸,我们能有的条件只有 $O(\log n)$ 求 $\mathrm{LCP}$。
那么 $\mathrm{LCP}$ 有什么用呢?
它又算不出来满足条件的最长字符串。
但是他是否**方便检测**长度为 $x$ 的符合限制字符串是否存在呢?
答案是**是的**。
考虑把一整段的 $height$ 数组划分为一块块的区间。
其中每个区间的 $l,r$ 都满足 $\min(height_{l\sim r})\ge x$。
因为我们对后缀排序了,所以这些后缀的至少有个长度为 $x$ 的公共 $\mathrm{LCP}$。
具体原因类似于上面推论 $1$ 的证明。
下面给个略证:
- 由推论 $1$ 得,$\mathrm{LCP}(sa_l,sa_r)\ge k$。
- 又对于 $i\in[l,r]$,$sa_l\le sa_i\le sa_r$。
- 所以其长度为 $k$ 的前缀均相等。
- 所以命题得证!
根据这个,就可以得到 $i\in[l,r],sa_i$ 符合条件。
那么贪心的想,想要放下这个长度为 $x$ 的串,就是其出现最左端点和最右端点的差值 $>x$。
也就是取 $L=\min(sa_{l\sim r}),R=\max(sa_{l\sim r})$。
如果满足 $r-l>x$,则长度为 $x$ 的串符合条件。
由此就可以写出这个 $check$。
显然的是具有单调性,考虑套个二分解决问题。
[std](https://www.luogu.com.cn/paste/n5b6vovx) 喵。
接着再来考虑原问题。
考虑到如果对于 $n$ 个串都构建 $\mathrm{SA}$,就无法保证我们 $check$ 出的是同一字符串。
所以采取奇怪分隔符间隔开所有字符串的方法把 $n$ 个字符串拼在一起,求一个 $\mathrm{SA}$。
接着把原本的 $L,R$ 扩展为 $L_{1\sim n},R_{1\sim n}$,判断对于任意的 $L_i,R_i$ 是否都满足 $R_i-L_i>x$ 即可。
[std](https://www.luogu.com.cn/paste/x3ulny0f) 喵。
$\LARGE{练习题}
LCS,LCS2,P5546 [POI2000] 公共串,LONGCS,DNA Sequencing。
都是 \mathrm{LCS} 问题喵,考虑求出 height 后,用双指针找区间外加单调队列求答案即可。
当然也可以二分,但是复杂度多一个 \log n。
std for P5546 喵。
8.4.2.P4070 [SDOI2016] 生成魔咒 \mathrm{SA}+字符串翻转
这个题,用到的东西,能叫他 \mathrm{PA},也就是 Prefix~Arrary 吗,不懂欸。
简要题意:
首先看到本质不同子串,首先考虑 \mathrm{SA}。
但是这个操作是在末尾加上字符,后缀在不断变化,显然的是不太好做。
那怎么办呢?
考虑把字符串翻转然后倒着扫。
也就相当于把 \mathrm{SA} 变为了 \mathrm{PA}。
那么每次多的就是一个新的前缀,也就是翻转串的一个新的后缀。
考虑本质不同的子串个数求法,是子串个数减去重复个数。
那么新的后缀就相当于,插入在了一个原本排序好的 height 序列中。
按照 rk 排序,重复的部分当且仅当新的后缀的前后与其求的 \mathrm{LCP} 嘛。
考虑扔进 set 里去,然后对于每个新的后缀找到其位置判断前后缀取 \max(\mathrm{LCP}) 即可。
具体可以看代码了。
std 喵。
8.4.3.P3975 [TJOI2015] 弦论 \mathrm{SA} 求第 k 小子串
比较经典了,但是我好像写的有点复杂。
简要题意:
- 给定长度为 n 的字符串 s 和两个数字 op,k。
- 若 op=0,则询问 s 的本质不同第 k 小子串。
- 否则询问 s 的第 k 小子串(可以本质相同)。
- 若不存在第 k 小,输出 -1。
-
n\le5\times10^5,k\le10^9
直接做这个问题还是稍微有点难度的,先来看一道他的子问题:SUBLEX。
这个问题中只有 op=0 的情况。
考虑 \mathrm{SA} 具有的优秀性质:
后缀有序。
这意味着后缀的前缀也是有序的。
那么我们就可以求出不重复子串个数的前缀和 ss 数组。
对于给定的 k,二分出第一个位置 i 满足 ss_i\ge k,接着直接算出右端点输出即可。
复杂度 O(T\times k),瓶颈在输出,所以其实可以不用二分的。
std 喵。
接着来考虑原问题中 op=1 的情况。
貌似不是很好处理?
因为要求的是字典序第 k 小,所以还是得先借用 \mathrm{SA} 后缀有序的优秀性质。
先按排序后的顺序枚举每个后缀,再枚举字母,二分出这个字母的右端点。
考虑类似于 op=0 时的前缀和,就可以快速查询出生成字符串个数。
找到之后再算出右端点输出即可。
因为枚举的后缀和字母大小都是单增的,所以肯定是第 k 小。
std。
具体实现有些细节喵。
8.4.4.P3181 [HAOI2016] 找相同字符 \mathrm{SA}+单调栈
简要题意:
- 给定长度为 n 的字符串 s 和长度为 m 的字符串 t。
- 问截取出两段相同子串有多少种方案。
-
考虑先转化题意,其本质即为算 s 的所有后缀与 t 的所有后缀的 \mathrm{LCP} 长度之和。
因为每个后缀的开头位置都不同,所以其公共前缀均为答案。
而对于两个字符串,其公共前缀数量即为 \mathrm{LCP} 长度。
这样便完成了第一步的转化。
接着发现 s 的所有后缀和 t 的所有后缀这个条件导致题目十分难处理。
不妨先来考虑这题的弱化版:P4248 [AHOI2013] 差异。
这个弱化版即为求所有后缀的 \mathrm{LCP} 长度之和。
考虑两个后缀 i,j 的 \mathrm{LCP} 长度即为 \min(height_{i+1\sim j})。
但是如果考虑枚举后缀的话复杂度就会难免来到 n^2 以上。
不难发现,height_i 对于这个区间 [l,r] 的答案有贡献当且仅当 height_i=\min(height_{l+1,r}),l+1\le i\le r。
考虑当一个区间单调的向左/右扩展时最小值单调,可以考虑单调栈维护求出每个 height_i 有贡献的最大区间 [l,r]。
那么具体的这个 height_i 的贡献即为 height_i\times(r-i)\times (i-l),也就是包含 i 的子区间都有贡献。
因为题目原因所以最后求出来的值还要乘 2,最后用总子串长度减去这个值即为答案。
std 喵。
接着来考虑原题目。
可以考虑容斥,那么答案即为 s+\#+t 的所有后缀的 \mathrm{LCP} 长度之和减去 s,t 的所有后缀的 \mathrm{LCP} 长度之和。
而求所有后缀的 \mathrm{LCP} 长度之和就是前文所述单调栈了。
std 喵。
8.4.5.P3649 [APIO2014] 回文串 \mathrm{SA}+\mathrm{Manacher}+\mathrm{ST} 表
一道感觉像是综合但又感觉像是单纯拼接算法的题目。
简要题意:
- 定义 s 的一个子串存在值为出现次数\times子串长度。
- 求所有回文子串中的最大存在值。
-
考虑一部分一部分地拆分解决。
首先考虑如何处理存在值,考虑使用 \mathrm{SA}+\mathrm{ST} 表的方式 O(\log n) 得到子串出现次数。
这样存在值就直接按照题意中给的公式计算即可。
接着考虑如何处理回文子串这个问题。
首先我们要知道一点,就是回文子串的总个数是线性的。
具体有关这一点的证明可以见回文树中的状态总数为线性的证明。
由这一点,我们考虑使用 \mathrm{Manacher} 求出 s 的回文子串。
在每求出一个新的回文子串时,使用 \mathrm{SA} 进行查询这个回文子串的存在值。
最后取 \max 即可。
std 喵。