[Str记录]Loj#6681. yww 与树上的回文串
command_block
·
·
个人记录
题意 : 给一棵树,每条边上有一个字符,求有多少点对 (x,y),满足路径 x\leftrightarrow y 上的边上的字符按顺序组成的字符串为回文串。
------------
> 寻寻觅觅,冷冷清清,凄凄惨惨戚戚。乍懂还懵时候,最难练习。三篇两道模板,怎敌他,赛场真题。
> 众里寻他千百度,蓦然回首,那题却在,LibreOJ 处。
考虑点分治,每次计算经过重心的串的贡献。
以中心为根,建立 $\rm Trie$ 树,进一步建立 $\rm AC$ 自动机。
观察一条经过重心的回文串,如下图所示 :
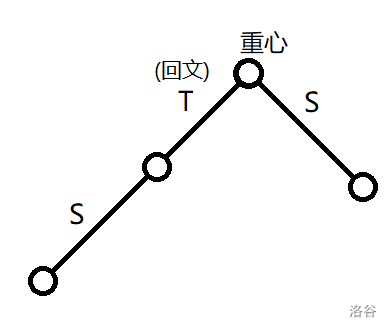
考虑先将 $S$ 一侧使用数据结构维护,再计算 $ST$ 一侧的贡献。
本题允许贡献差分,所以只需静态数据结构。
$T$ 是一个串的回文前缀,根据回文 $\rm Border$ 理论,可以被划分成 $O(\log n)$ 个等差序列。
回文前缀可以暴力 $\rm Hash$ 求解。
现在问题就转化成这样了 :
给出一棵 $\rm Trie$ 树,对某个串,询问其长度为一个等差序列的后缀的匹配次数总和。
根据 $\rm AC$ 自动机的经典理论,若求长度为 $k$ 的后缀的匹配次数总和,只需要查看 $fail$ 树的长度为 $k$ 的祖先串的贡献即可。
对于公差 $\leq \sqrt{n}$ 的等差序列,在 $fail$ 树上预处理模分类树上前缀和。
若长度等差序列中,公差为 $d$ ,首项为 $l$,末项为 $r$,只需要跳到长度 $\leq r$ 的第一个点,加上祖先中模 $d$ 同余的点权和,再在长度 $< l$ 的第一个点减一次。
由于模分类前缀和空间占用太大,不能直接预处理(否则要可持久化),所以要把上述询问离线。
对于公差 $> \sqrt{n}$ 的等差序列,元素个数总和 $O\Big(\sum\limits_{k=1}\sqrt{n}/2^k\Big)=O(\sqrt{n})$ 的,暴力即可。
单次处理复杂度为 $O(n\sqrt{n})$ ,总复杂度为 $T(n)=2T(n/2)+O(n\sqrt{n})=O(n\sqrt{n})$。
这题数据有点水,暴力枚举回文前缀也可以过……
```cpp
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<vector>
#include<queue>
#include<cmath>
#define ll long long
#define pb push_back
#define MaxN 50500
using namespace std;
vector<int> g[MaxN],l[MaxN];
int st[MaxN],tot,ms[MaxN],siz[MaxN];
bool vis[MaxN];
void pfs(int u,int fa)
{
siz[st[++tot]=u]=1;ms[u]=0;
for (int i=0,v;i<g[u].size();i++)
if ((v=g[u][i])!=fa&&!vis[v]){
pfs(v,u);
siz[u]+=siz[v];
ms[u]=max(ms[u],siz[v]);
}
}
int grt(int u)
{
tot=0;pfs(u,0);
int rt=0;
for (int i=1,u;i<=tot;i++){
u=st[i];
ms[u]=max(ms[u],tot-siz[u]);
if (ms[u]<ms[rt])rt=u;
}return rt;
}
const int mod=1000000007,INF=1000000000;
int pw2[MaxN],BS;
struct ACAM
{
struct Node{int t[2],f,cnt;}a[MaxN];
struct Data{int d,l,r;};
vector<Data> b[MaxN];
int len[MaxN],sh[MaxN],sl[MaxN];
void dfs1(int u,int h)
{
if (sh[len[u]/2]==h&&len[u]){
if (b[u].empty())b[u].pb((Data){INF,len[u],len[u]});
else {
Data now=b[u].back();
if (now.d==INF)
b[u].back()=(Data){len[u]-now.l,now.l,len[u]};
else if (len[u]==now.r+now.d)
b[u].back().r=len[u];
else b[u].pb((Data){INF,len[u],len[u]});
}
}
for (int c=0,v;c<=1;c++){
if (!(v=a[u].t[c]))continue;
len[v]=len[u]+1;
sl[len[v]]=c;
sh[len[v]]=(sh[len[u]]+pw2[len[u]]*c)%mod;
b[v]=b[u];
dfs1(v,
(len[u]&1) ? (h*2+c)%mod
: (1ll*h*2+c-sl[len[u]/2+1]*pw2[len[u]/2]+mod)%mod
);
}
}
vector<int> g[MaxN];
int tn;
void buildfail()
{
static queue<int> q;
for (int c=0;c<=1;c++)
if (a[1].t[c]){
a[a[1].t[c]].f=1;
q.push(a[1].t[c]);
}else a[1].t[c]=1;
while(!q.empty()){
int u=q.front();q.pop();
for (int c=0,v;c<=1;c++){
v=a[a[u].f].t[c];
if (a[u].t[c]){
a[a[u].t[c]].f=v;
q.push(a[u].t[c]);
}else a[u].t[c]=v;
}
}for (int i=2;i<=tn;i++)
g[a[i].f].pb(i);
}
int sf[MaxN],top,o0[MaxN];
ll ret;
vector<Data> b2[MaxN];
void dfs2(int u)
{
sf[++top]=u;
for (int i=0;i<b[u].size();i++){
int l=len[u]-b[u][i].r,r=len[u]-b[u][i].l,d=b[u][i].d;
if (d>BS){
ll buf=0;
for (int j=l;j<=r;j+=d)buf+=o0[j];
ret+=buf*a[u].cnt;
}else {
int ul=sf[lower_bound(sl+1,sl+top,l)-sl-1],
ur=sf[upper_bound(sl+1,sl+top,r)-sl-1];
if (ul!=ur){
if (ul)b2[ul].pb((Data){d,l%d,-a[u].cnt});
if (ur)b2[ur].pb((Data){d,l%d,a[u].cnt});
}
}
}o0[sl[top]=len[u]]+=a[u].cnt;
ret+=1ll*(a[u].cnt-1)*a[u].cnt/2;
for (int i=0;i<g[u].size();i++)dfs2(g[u][i]);
o0[sl[top--]]-=a[u].cnt;
}
int o[105][105];
void dfs3(int u)
{
for (int c=1;c<=BS;c++)
o[c][len[u]%c]+=a[u].cnt;
for (int i=0;i<b2[u].size();i++)
ret+=1ll*b2[u][i].r*o[b2[u][i].d][b2[u][i].l];
for (int i=0;i<g[u].size();i++)dfs3(g[u][i]);
for (int c=1;c<=BS;c++)
o[c][len[u]%c]-=a[u].cnt;
}
ll calc()
{
ret=0;
dfs1(1,0);
buildfail();
dfs2(1);dfs3(1);
return ret;
}
void Init()
{
for (int i=1;i<=tn;i++)
{b[i].clear();b2[i].clear();g[i].clear();}
memset(a,0,sizeof(Node)*(tn+2));tn=1;
}
}T;
void dfs(int u,int t,int fa)
{
T.a[t].cnt++;
for (int i=0,v;i<g[u].size();i++)
if ((v=g[u][i])!=fa&&!vis[v]){
dfs(v,
T.a[t].t[l[u][i]] ? T.a[t].t[l[u][i]] : T.a[t].t[l[u][i]]=++T.tn
,u);
}
}
ll ans=0;
void solve(int u)
{
if (tot==1)return ;
BS=sqrt(tot/6);
T.Init();dfs(u,1,0);ans+=T.calc();
vis[u]=1;
for (int i=0,v;i<g[u].size();i++)
if (!vis[v=g[u][i]]){
T.Init();
dfs(v,T.a[1].t[l[u][i]]=++T.tn,u);
ans-=T.calc();
}
for (int i=0,v;i<g[u].size();i++)
if (!vis[v=g[u][i]])
solve(grt(v));
}
int n;
int main()
{
scanf("%d",&n);
pw2[0]=1;
for (int i=1;i<=n;i++)pw2[i]=pw2[i-1]*2%mod;
for (int i=1,u,v,w;i<n;i++){
scanf("%d%d%d",&u,&v,&w);
g[u].pb(v);l[u].pb(w);
g[v].pb(u);l[v].pb(w);
}ms[0]=n;solve(grt(1));
printf("%lld",ans);
return 0;
}
```