数学-三角函数
kebingyi
·
·
个人记录
基本概念
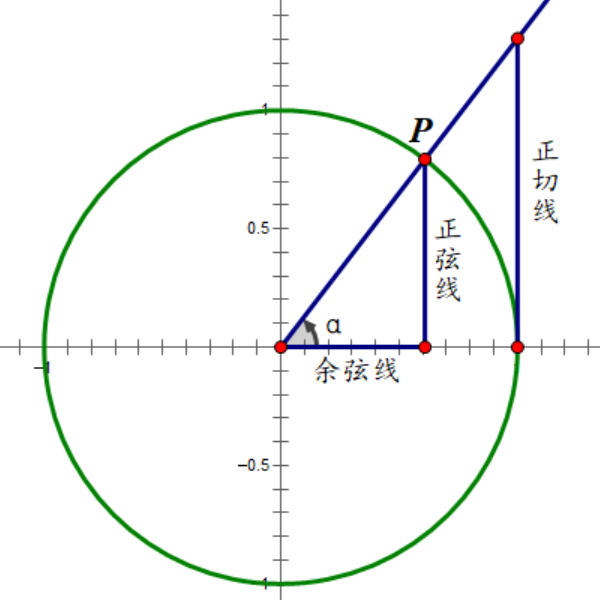
在平面直角坐标系中,设∠α终边上任意一点P的坐标是(x,y),它与原点的距离为r=\sqrt{x^2+y^2},那么:
$\begin{aligned}\tanα=\frac{y}{x}\end{aligned}$,$\begin{aligned}\cotα=\frac{x}{y}\end{aligned}$,
$\begin{aligned}\secα=\frac{r}{x}\end{aligned}$,$\begin{aligned}\cscα=\frac{r}{y}\end{aligned}$。
## 三角函数性质
(以下只研究$\sin,\cos,\tan,\cot$的性质,其余类似可得)
1. 奇偶性
$y=\sin x,\ y=\tan x,\ y=\cot x$在其定义域上为奇函数
$y=\cos x$在其定义域上为偶函数
2. 单调性
$y=\sin x$在$\begin{aligned}[-\frac{π}{2}+2kπ,\frac{π}{2}+2kπ]\end{aligned}$上为增函数,在$\begin{aligned}[\frac{π}{2}+2kπ,\frac{3π}{2}+2kπ]\end{aligned}$上为减函数;
$y=\cos x$在$[-π+2kπ,2kπ]$上为增函数,在$[2kπ,π+2kπ]$上为减函数;
$y=\tan x$在$\begin{aligned}(-\frac{π}{2}+kπ,\frac{π}{2}+kπ)\end{aligned}$上为增函数;
$y=\cot x$在$(kπ,π+kπ)$上为减函数;
3. 周期性
$\sin,\cos$的周期为$2π
\tan,\cot$的周期为$π
诱导公式
(以下只考虑\sin,\cos,\tan的诱导公式,其余3个分别与它们互为倒数,类似可得)
\sin(α+2kπ)=\sinα,\cos(α+2kπ)=\cosα,\tan(α+2kπ)=\tanα
\sin(π+α)=-\sinα,\cos(π+α)=-\cosα,\tan(π+α)=\tanα
\sin(-α)=-\sinα,\cos(-α)=\cosα,\tan(-α)=-\tanα
\sin(π-α)=\sinα,\cos(π-α)=-\cosα,\tan(π-α)=-\tanα
\begin{aligned}\sin(\frac{π}{2}-α)=\cosα,\cos(\frac{π}{2}-α)=\sinα,\tan(\frac{π}{2}-α)=\cotα\end{aligned}
\begin{aligned}\sin(\frac{π}{2}+α)=\cosα,\cos(\frac{π}{2}+α)=-\sinα,\tan(\frac{π}{2}+α)=-\cotα\end{aligned}
三角恒等变换
- 和差角公式
\sin(α+β)=\sinα\cosβ+\cosα\sinβ\ ,\ \sin(α-β)=\sinα\cosβ-\cosα\sinβ
\cos(α+β)=\cosα\cosβ-\sinα\sinβ\ ,\ \cos(α-β)=\cosα\cosβ+\sinα\sinβ
\begin{aligned}\tan(α+β)=\frac{\tanα+\tanβ}{1-\tanα\tanβ}\ ,\ \tan(α-β)=\frac{\tanα-\tanβ}{1+\tanα\tanβ}\end{aligned}
- 倍角半角公式
\sin2α=2\sinα\cosα\to(\sinα±\cosα)^2=1±\sin2α
\cos2α=\cos^2α-\sin^2α=2\cos^2α-1=1-2\sin^2α
\begin{aligned}\tan2α=\frac{2\tanα}{1-\tan^2α}\end{aligned}
\sin3α=3\sinα-4\sin^3α=4\sinα\sin(60-α)\sin(60+α)
\cos3α=4\cos^3α-3\cosα=4\cosα\cos(60-α)\cos(60+α)
\tan3α=\tanα\tan(60-α)\tan(60+α)
\begin{aligned}\sin\frac{α}{2}=±\sqrt{\frac{1-\cosα}{2}}\rightarrow\sin^2\frac{α}{2}=\frac{1-\cosα}{2}\end{aligned}
\begin{aligned}\cos\frac{α}{2}=±\sqrt{\frac{1+\cosα}{2}}\rightarrow\cos^2\frac{α}{2}=\frac{1+\cosα}{2}\end{aligned}
\begin{aligned}\tan\frac{α}{2}=\frac{1-\cosα}{\sinα}=\frac{\sinα}{1+\cosα}=±\sqrt{\frac{1-\cosα}{1+\cosα}}\end{aligned}
- 万能公式
\begin{aligned}\sinα=\frac{2\tan\frac{α}{2}}{1+\tan^2\frac{α}{2}}\end{aligned}
\begin{aligned}\cosα=\frac{1-\tan^2\frac{α}{2}}{1+\tan^2\frac{α}{2}}\end{aligned}
\begin{aligned}\tanα=\frac{2\tan\frac{α}{2}}{1-\tan^2\frac{α}{2}}\end{aligned}
- 和差化积公式
\begin{aligned}\sinα\cosβ=\frac{1}{2}[\sin(α+β)+\sin(α-β)]\end{aligned}
\begin{aligned}\cosα\sinβ=\frac{1}{2}[\sin(α+β)-\sin(α-β)]\end{aligned}
\begin{aligned}\cosα\cosβ=\frac{1}{2}[\cos(α+β)+\cos(α-β)]\end{aligned}
\begin{aligned}\sinα\sinβ=-\frac{1}{2}[\cos(α+β)-\cos(α-β)]\end{aligned}
- 积化和差公式
\begin{aligned}\sinα+\sinβ=2\sin\frac{α+β}{2}\cos\frac{α-β}{2}\end{aligned}
\begin{aligned}\sinα-\sinβ=2\cos\frac{α+β}{2}\sin\frac{α-β}{2}\end{aligned}
\begin{aligned}\cosα+\cosβ=2\cos\frac{α+β}{2}\cos\frac{α-β}{2}\end{aligned}
\begin{aligned}\cosα-\cosβ=-2\sin\frac{α+β}{2}\sin\frac{α-β}{2}\end{aligned}
- 辅助角公式(合一变形公式)
\begin{aligned}a\sin x+b\cos x=\sqrt{a^2+b^2}\sin(x+φ)\end{aligned}$,其中$\begin{aligned}\sinφ=\frac{b}{\sqrt{a^2+b^2}},\cosφ=\frac{a}{\sqrt{a^2+b^2}},\tanφ=\frac{b}{a}\end{aligned}
三角形中的三角函数
- 正弦定理
\begin{aligned}\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\end{aligned}
- 余弦定理
c^2=a^2+b^2-2ab\cos C$ → $\begin{aligned}\cos C=\frac{a^2+b^2-c^2}{2ab}\end{aligned}
b^2=c^2+a^2-2ca\cos B$ → $\begin{aligned}\cos B=\frac{c^2+a^2-b^2}{2ca}\end{aligned}
a^2=b^2+c^2-2bc\cos A$ → $\begin{aligned}\cos A=\frac{b^2+c^2-a^2}{2bc}\end{aligned}
- 射影定理
a=b\cos C+c\cos B
b=c\cos A+a\cos C
c=a\cos B+b\cos A
- 恒等式
\begin{aligned}\sin A+\sin B+\sin C=4\cos\frac{A}{2}\cos\frac{B}{2}\cos\frac{C}{2}\end{aligned}
\begin{aligned}\cos A+\cos B+\cos C=1+4\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}\end{aligned}
\tan A+\tan B+\tan C=\tan A\tan B\tan C
\sin2A+\sin2B+\sin2C=4\sin A\sin B\sin C
\cos2A+\cos2B+\cos2C=-1-4\cos A\cos B\cos C
\begin{aligned}\cot\frac{A}{2}+\cot\frac{B}{2}+\cot\frac{C}{2}=\cot\frac{A}{2}\cot\frac{B}{2}\cot\frac{C}{2}\end{aligned}
\begin{aligned}\tan\frac{A}{2}\tan\frac{B}{2}+\tan\frac{B}{2}\tan\frac{C}{2}+\tan\frac{C}{2}\tan\frac{A}{2}=1\end{aligned}