浅谈 LCA

> LCA（`Least Common Ancestors`），最近公共祖先，定义为两节点最近的公共祖先~~好像是废话~~ 前置芝士： - 图论 **此文章中均设 $\mathrm{fa}_i$ 为 $i$ 的父亲，$\mathrm{dep}_i$ 为 $i$ 的深度。** ## 暴力 显然我们找出节点的所有祖先再 $n^2$ 比较即可。 当然你也可以一层层往上跳。 时间复杂度是 $\mathcal{O}(n^2)$。 ## 倍增 我们思考一次性跳多步，减少时间复杂度。 考虑二进制拆分。 考虑用 dp 预处理： 设 $f_{i,j}$ 为 $i$ 往上跳 $2j$ 步到达的点，即可以使用以下转移方程： $\begin{cases} f_{i,0}=\mathrm{fa}_i\\ f_{i,j}=f_{f_{i,j-1},j-1} \end{cases}$ 所以我们设 $\mathrm{lg2}_k=\lfloor\log_2k\rfloor$，即 直接从 $\mathrm{lg2}_i$ **往下**枚举即可。 --- 整理下，如果我们求 $\mathrm{LCA}(u,v)$： 默认 $\mathrm{dep}_u<\mathrm{dep}_v$（如果不满足根据 $\mathrm{LCA}(u,v)=\mathrm{LCA}(v,u)$ 交换 $u,v$ 即可） 过程如下： 1. 预处理 $f$ 数组 2. 将 $u,v$ 跳至同一层 3. 如果相等直接返回 4. 否则继续跳，直到它们都跳到 LCA 的**往下一层**。 这个在**链上**极其好用。 代码： ```cpp int LCA(int u,int v) { if (dep[u]<dep[v]) swap[u][v]; //交换 while (dep[u]>dep[v]) //预处理 u=fa[u][lg2[dep[u]-dep[v]-1]]; if (u==v) return u; //跳出 for (int i=lg2[dep[u]-1];i>=0;--i) if (fa[u][i]!=fa[v][i]) u=fa[u][i],v=fa[v][i]; //继续跳 return fa[u][0]; } ``` ## RMQ求解 > RMQ（`Range [Minimum/Maximum] Query`），区间最值问题。 首先我们要了解一个**离线**求 RMQ 的数据结构——st表（`Sparse Table`） 因为 st 表也是倍增思想，所以转移方程也会很像： - 设 $f_{i,j}$ 表示 $i$ 开始，$2j$ 个元素的最值（不一定连续） - 则 $f_{i,j}=\min(\mathrm{or}\;\max)(f_{i,j-1},f_{i+2^{j-1},j-1})$（切开求解） 首先考虑最值允许区间重叠： $$\max(a,b,c)=\max(\max(a,b),\max(b,c))$$ 我们即肯定能找到一个 $x$ 使得 $[l,l+2^x-1]$ 和 $[r-2^x+1,r]$ 的最值与 $[l,r]$ 的最值相等。 则这个 $x$ 很容易想出（$l,r$ 之间有 $r-l+1$ 个元素）： $$\large x=\log_2(r-l+1)$$ *** 我们回归 LCA。 首先我们要了解**欧拉序**。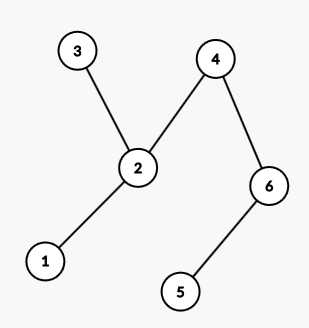 以此图为例：  设 $4$ 为树根： 则它的属性： - DFS 序：$4,2,3,1,6,5$； - 带上回溯的 DFS 序：$4,2,3,2,1,2,4,6,5$。 其中“带上回溯的 DFS 序”即为欧拉序。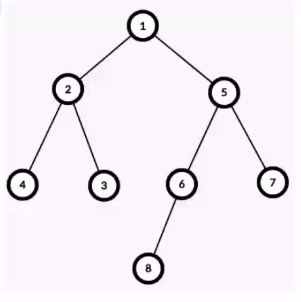 *** 我们看看此图：  比如我们找 $4,8$ 的 LCA： 写出欧拉序： $$1,2,4,2,3,2,1,5,6,8,6,5,7,5,1$$ 转换为深度： $$1,2,3,2,3,2,1,2,3,4,3,2,3,2,1$$ 找出 $4,8$ 之间区域： $$1,2,\bold{3,2,3,2,1,2,3,4},3,2,3,2,1$$ 正好深度最低的点就是 $1$，它们的 LCA！ 这样就把 LCA 转换为了 RMQ，st表求解即可。 ## Tarjan 算法 我们引用 rxz 的话： > 一个熊孩子 Link 从一颗有根树的最左下节点灌岩浆，Link 表示很讨厌这种倒着长的树，岩浆会不断蔓延到整个树。 > > 如果岩浆灌满了一颗子树 Link 发现树的右边有棵更深的子树，则 Link 会去灌岩浆。 > > 岩浆只有迫不得已的情况才会升高，找新子树进行注入。 > > 机(yu)智(chun)的 Link 发现了一个求 LCA 的好办法，即：如果两个节点都被岩浆烧掉时，它们的 LCA 即为那棵子树上岩浆最高的位置。 即按 rxz 描述的写即可，伪代码如下： ```cpp void tarjan() { for (u的所有儿子v) { tarjan(v); merge(u,v); //并查集 } for (所有与u有关的查询(u,v)) if (vis[v]) ans[id]=find(v); } ``` ## 树剖写法 > 树剖，即树链剖分，将树变为链的方法，可以应对某些~~毒瘤~~出题人将数列上问题转移到树上的情况。 我们求 LCA 用的是**轻重链剖分**，也就是将树变成轻链和重链。 我们首先给出一些定义： - 重儿子：某节点儿子中子树最大的儿子（相等随便选一个） - 轻儿子：除重儿子以外的所有儿子 - 重边：爹连到重儿子的边（爹不一定是重儿子） - 轻边：除重边外所有边 - 重链：重边组成的链（**轻叶节点自成重链**） - 轻链：轻边组成的链 我们树剖需要的数组： - $\mathrm{siz}_i$ 表示以 $i$ 为根的子树大小。 - $\mathrm{hvs}_i$ 表示 $i$ 节点的重儿子。 - $\mathrm{ltp}_i$ 表示 $i$ 所在的重链头（深度最浅节点）。 树刨和莫队等等一样都是*优雅的暴力* ，会被轻重链交替的数据或者全是轻链的数据卡死。 首先两次 DFS： - 第一次求 $\mathrm{fa}$、$\mathrm{dep}$、$\mathrm{siz}$、$\mathrm{hvs}$。 - 第二次只求 $\mathrm{ltp}$。 然后轻重链交替跳 LCA 即可（适时原 地 踏 步）。