你也能证明四色定理
cancan123456
·
2023-02-02 22:16:25
·
个人记录
似乎很显然的证明
考虑对图 G 的每个顶点染色,使得每条边的两个顶点不同色,我们记满足条件的最小的所需颜色数为 \chi(G) 。
再定义图 G 中的最大完全图子图的点数为 \omega(G) 。
那么我们就考虑是否有……
\chi(G)\le\omega(G)
如果能够证明这个命题,那么根据平面图中没有 K_5 ①,即 \omega(G)\le4 ,就可以得出所有平面图 G 都满足 \chi(G)\le4 ,这就是四色定理了。
①:K_n 是一个 n 个点的图,并且每两个点之间都有边。
但是很遗憾,这个猜想是错的,考虑下面这个图:
我们可以发现 \omega(G)=4 ,但是 \chi(G)>4 ,证明:
注意到显然有 \chi(G)\ge\omega(G)=4 ,所以 \chi(G)\ge4 。
下面证明 \chi(G)\not=4 ,考虑反证法,注意到 1,2,3,4 是一个 K_4 ,所以不妨设 1,2,3,4 的颜色分别是 1,2,3,4 ,而 5,6 与 1,3,4 都有边,那么 5,6 的颜色都只能是 2 ,但是 5,6 之间有边,所以 \chi(G)\not=4 。
于是就有 \chi(G)>4 。
同理,有无数个图 G 满足 \omega(G)=4 但是 \chi(G)>4 ,我们需要证明它们都不是平面图。
似乎正确的证明
这个证明来源于 Kempe,时间是 1879 年,在这个证明中我们考虑由区域组成的地图而不是图。
Lemma 1
对于任意一张地图,都存在一个顶点使得其度数小于 6 。
考虑反证法,对于任意图,有欧拉定理:
V-E+F=2
考虑边的计数,每个顶点至少与 3 条边相邻:
2E=\sum_v\deg(v)\ge\sum_v3\ge3V
每个面至少与 6 条边相邻:
2E=\sum_f\deg(f)\ge\sum_f6\ge6F
代入欧拉公式:
2=V-E+F\le\frac23E-E+\frac13E=0
这就证明了至少一个顶点的度数小于 6 。
Definition 1
一个 Kempe 链是极大的顶点集合,满足该集合内顶点的颜色只有 2 种以下,且相邻顶点不同色。
Definition 2
反色操作作用于一个 Kempe 链,将其所有顶点的颜色变成该 Kempe 链中的另一种颜色。
显然,对一个合法的图进行一次反色操作后,仍然是一个合法的图。
Definition 3
一个三区共点为一个点,满足其周围有且仅有三个区域。
Lemma 2
对于任意区域 X ,如果 \deg(X)=4 ,且其四个相邻区域 A_1,A_2,A_3,A_4 颜色互不相同,一定存在 i\not=j ,满足 X,A_i,A_j 不存在三区共点。
考虑反证法,如果对于任意 i\not=j ,X,A_i,A_j 的三区共点都存在,那么由于 A_1 与 X 的一条邻边有且仅有两个顶点,所以最优情况下也需要两条邻边才可能构成三个三区共点,所以 X+A_1 构成了一个环形,将其去掉后会形成两个不相邻的区域,且 A_2,A_3,A_4 必然有两个在第一个区域,另一个在第二个区域,所以显然 A_2,A_3,A_4 的三区共点不可能同时存在。
Lemma 3
对于任意区域 X ,如果 \deg(X)=4 ,且其四个相邻区域 A_1,A_2,A_3,A_4 颜色互不相同,如果 A_1,A_2 在同一个 Kempe 链中,那么 A_3,A_4 一定不在一个 Kempe 链中。
考虑反证法,设 A_1,A_2 都在 Kempe 链 U 中,那么 U+X 一定构成了一个环形,去掉 U 之后会将原图分为两个互不相邻,但都与 X 相邻的区域,显然 A_3,A_4 必须分别在两个区域中,由于 U_1 中的颜色与 A_3,A_4 都不相同,所以 A_3,A_4 不可能在一个 Kempe 链中。
Lemma 4
对于任意区域 X ,如果 \deg(X)=5 ,且其五个相邻区域有 4 种颜色,根据抽屉原理,一定有且仅有两个区域 A_1,A_2 的颜色相同,剩下的区域 B_1,B_2,B_3 颜色互不相同,且 B_1,B_2,B_3 两两在同一 Kempe 链中,那么一定存在一个 i 使得 A_1,B_i,X 不存在三区共点。
考虑反证法,设对于所有 i ,A_1,B_i,X 都存在三区共点,由 Lemma 3 的证明过程可知 A_1+X 一定构成了一个环,去掉之后将原图分割为若干区域 P_1,P_2,\dots,P_k ,显然 B_1,B_2,B_3 一定在一个区域内,不妨设 B_1,B_2,B_3 在 P_1 内,容易得出 P_2,\dots,P_k 与 X 的边界都被 A_2 占据,现在将 A=A_1+P_2+\cdots+P_k 看作一个国家,这个意义下 \deg(X)=4 ,由 Lemma 3 可知 B_1,B_2,B_3,A 中至少由一对不在一个 Kempe 链中,由假设知道 B_1,B_2,B_3 两两在一个 Kempe 链中,所以 B 与 B_1,B_2,B_3 中的至少一个不在一个 Kempe 链中,所以 A 与至少一个 B_i 没有三区共点。
Lemma 5
对于任意区域 X ,如果 \deg(X)=5 ,且其五个相邻区域有 4 种颜色,根据抽屉原理,一定有且仅有两个区域 A_1,A_2 的颜色相同,剩下的区域 B_1,B_2,B_3 颜色互不相同,且 B_1,B_2,B_3 两两在同一 Kempe 链中,那么一定存在 i\not=j 使得 A_1,B_i,X 不存在三区共点且 A_2,B_j,X 不存在三区共点。
考虑反证法,首先证明 A_1,X 一定只有一条邻边,如果有两条及以上,那么 A_1+X 必然构成一个环形,将图分成与 X 相邻但是互不相邻的 P_1,P_2,\dots,P_k ,显然 B_1,B_2,B_3 必然都从属于一个区域,不妨设其为 P_1 ,那么如果 A_2 在 P_1 中,那么 P_2 区域就没有邻国了,否则,如果 A_2 在 P_2 中,那么 A_2,B_i,X 就都不能存在三区共点,这是显然可以找出 i\not=j 使得 A_1,B_i,X 不存在三区共点且 A_2,B_j,X 不存在三区共点。同理可得 A_2,X 也只有一条邻边。
然后证明 B_3,X 一定只有一条邻边,如果有两条及以上,那么 B_3+X 必然构成一个环形,将图分成与 X 相邻但是互不相邻的 P_1,P_2,\dots,P_k ,显然 B_1,B_2 必然都从属于一个区域,不妨设其为 P_1 ,那么如果 A_2 在 P_1 中,
Lemma 6
对于任意区域 X ,如果 \deg(X)=5 ,且其五个相邻区域有 4 种颜色,根据抽屉原理,一定有且仅有两个区域 A_1,A_2 的颜色相同,剩下的区域 B_1,B_2,B_3 颜色互不相同,且 B_1,B_2,B_3 两两在同一 Kempe 链中,A_1,B_1,X 不存在三区共点,A_2,B_2,X 不存在三区共点,B_3 与 A_1 在同一 Kempe 链中,设 U_1 为 A_1 所处的含有 B_1 的 Kempe 链中,设 U_2 为 A_2 所处的含有 B_2 的 Kempe 链中,那么 U_1,U_2 一定不连通。
考虑反证法,如果 U_1,U_2 连通,那么 U_1+U_2+X 一定构成了一个环,必然会分割出两个与 X 相邻但是互不连通的区域 P,Q ,因为 U_1+U_2+X 中不含 B_3 的颜色,所以 B_3 不在 U_1,U_2 中,不妨设 B_3 在 P 中,则 B_1,B_2 一定在 Q 中,那么 B_3 必然不能与 B_1,B_2 在一个 Kempe 链中。
证明
考虑归纳法,设对于某个正整数 n ,满足所有定点数小于等于 n 的平面图都可以用 4 种颜色染色,考虑某个 n+1 个顶点的图,根据 Lemma 1,一定有一个顶点 X 满足 \deg(X)\le5 ,我们先把这个顶点删掉,就变成了 n 个顶点的图,根据归纳假设,这个新图可以用 4 种颜色染色,现在考虑将 X 加回来,对 \deg(X) 分类讨论。
Case 1 周围颜色数量小于等于 3
将剩下的颜色选一个给 X 即可。
Case 2 \deg(X)=4
设与 X 连接的四个顶点为 A_1,A_2,A_3,A_4 ,由 Lemma 2 可知一定存在 i\not=j ,使得 A_i,A_j,X 不存在三区共点。
Case 2.1 A_1,A_2 不在一个 Kempe 链中
将 A_1 所处的含有 A_2 颜色的 Kempe 链反色,归结为 Case 1。
Case 2.2 A_1,A_2 在同一 Kempe 链中
由 Lemma 3 可知此时 A_3,A_4 肯定不在一个 Kempe 链中,归结为 Case 2.1。
Case 3 \deg(X)=5
根据抽屉原理,这 5 个顶点中一定有且仅有两个顶点同色,不妨设其为 A_1,A_2 ,另外 3 个不同色的顶点为 B_1,B_2,B_3 。
Case 3.1 B_1,B_2,B_3 中有两个顶点不在同一 Kempe 链中
不妨设 B_1,B_2 不在一个 Kempe 链中,将 B_1 所处的含有 B_2 颜色的 Kempe 链反色,归结为 Case 1。
Case 3.2 B_1,B_2,B_3 中任意两个顶点都在同一 Kempe 链中
由 Lemma 4 和 Lemma 5 可知,存在 i\not=j 使得 A_1,B_i,X 不存在三区共点,A_2,B_j,X 不存在三区共点,不妨设 i=1,j=2 ,继续分类。
Case 3.2.1 B_3,A_1 不在同一 Kempe 链中,B_3,A_2 也不同一个 Kempe 链中
将 B_3 所处的包含 A_1 颜色的 Kempe 链反色,然后将 B_3 原来的颜色给 X ,结束。
Case 3.2.2 B_3 与 A_1,A_2 至少一个在同一 Kempe 链中
不妨设 B_3,A_1 在同一 Kempe 链中。
我们设 A_1 所处的包含 B_1 颜色的 Kempe 链为 U_1 ,A_2 所处的包含 B_2 颜色的 Kempe 链为 U_2 ,由 Lemma 6 可知 U_1,U_2 不连通。
将 U_1,U_2 反色,然后将 A_1,A_2 原来的颜色给 X 。
于是,我们证明了四色定理对于任意的 n 都成立。
当然这是不可能的,考虑下面这个图:
容易验证其满足 Case 3.2.2 的要求,U_1=\{A_1,P_1\},U_2=\{A_2,P_2\} ,但是 U_1,U_2 连通了,这就意味着 Lemma 6 是错的。
Appel, Haken 以及 Kock 的证明
他们写了一本书来描述四色定理的证明,从网上可以下载到两部分,一部分 62 页,一部分 77 页,全是英文。
由于有些图实在是太大了,就不放图片了。
Part I
Part II
第一部分:放电
1. 介绍
我们首先按照时间顺序描述导致本文工作的早期结果。四色定理的证明需要本文第 2 节和第 3 节的结果以及第二部分的可约性结果。第 4 节和第 5 节将致力于解释四色问题的困难和证明的异常性质。
Kempe [19] 在 1879 年第一次尝试证明四色定理,他证明了这个问题可以在“正规平面图”上解决。正规平面图的每个面都是简单多边形,并且每个顶点只连接了三条边,对于这种图,可以从欧拉公式推导出:
4p_2+3p_3+2p_4+p_5=\sum_{k=7}^{k_\text{max}}(k-6)p_k+12\tag{1.1}
其中 p_i 是 i 边形的数量,k_\text{max} 是多边形的边数的最大值,显然可以得出对于所有正规平面图,都有至少一个多边形使得其边数小于 6 。
为了证明四色定理,我们引入一个数 p 表示图中多边形数目,显然有 p=\sum p_i ,Kempe 采用数学归纳法,即假设对于所有 p\le r 的图都是满足四色定理了,然后考虑一个新的正规平面图 M_{r+1} ,然后他进行分类讨论:M_{r+1} 含有一个有两条边的多边形 P_2 ,或者有三条边的多边形 P_3 ,或者有四条边的多边形 P_4 ,或者有五条边的多边形 P_5 ,为了满足等式 (1.1) ,这些情况必定有至少一种成立。在每个情况中,他都构造一个图 M_r ,通过删除 M_{r+1} 中的一个多边形 P_k ,应用归纳假设,M_r 可以用四种颜色染色,显然,删掉 P_2,P_3 的情况是可以简单地对 M_{r+1} 进行染色。为了对待 P_4,P_5 ,Kempe 引入了 Kempe 链来处理这些情况,得到 M_{r+1} 的正确染色。
当 Kempe 成功地处理了 P_4 的情况,他在处理 P_5 的时候犯了一个小错误,Heawood 在 1890 年指出了这一问题。然而,Kempe 的思路足以证明五色定理,并且若存在一个四色定理的反例,那么其必定不包含二边形、三角形或者四边形,将其代入 (1,1) 中我们可以得到:
p_5=\sum_{k=7}^{k_\text{max}}(k-6)p_k+12\tag{1.2}
这能够说明最小反例一定包含至少 12 个五边形。
自 1890 年以来,人们不断尝试证明四色定理,这些尝试分为两类:(i) 试图修复 Kempe 工作中的缺陷;(ii) 试图找到新方法来证明四色定理。(i) 又分为两种类型:(i)(a) 试图找到一个更强大的处理五边形的方法,即证明最小反例不存在任何五边形,进而推导出最小反例不存在;(i)(b) 试图在不同方向中推广 Kempe 的思路,即用另外一些多边形的构型来替代五边形。本文中的方法属于 (i)(b),因此下面将着重观察 (i)(b) 方向的进展。
在 1904 年,Wernicke [28] 证明了所有 p_2=p_3=p_4=0 的正规平面图都一定存在一个五边形满足其与一个五边形或六边形相邻,1922 年,Franklin [14] 改进了这个结果,他证明了必然出现两个相邻的五边形或者一个连接着两个六边形的五边形。1940 年,Lebesgue [21] 给出了大量构型。我们将这样的构型成为不可避免集合。
对于四色问题,Birkhoff 提出了三种选择:
1. 四色猜想是错的。
2. 我们可以找到一组可约且不可避免的集合,这将证明四色猜想。
3. 四色猜想是正确的,但是需要其他更复杂的方法来证明。
然而,他并没有对他支持哪些方案发表意见。
Birkhoff 在 [10] 中描述的证明可约性的方法已被许多研究者应用,特别是 Franklin [14]、Errera [13]、Winn [29]、Chojnacki [11]、Arthur Bernhart [7]、Heesch [16] [17]、Ore & Stemple [23]、Frank Bernhart [8]、Allaire & Swart [2]、Mayer [22] 和 Allaire [1]。Heesch [19]、Tutte & Whitney [27] 对这个算法进行了更详细的描述。在最近的应用 [12] [17] [1] [2] [9] [20] 中,这个算法由电子计算机执行,通过这些方法获得的最小可约构型均由四个多边形组成,这些多边形围绕着一条边,Birkhoff(如上所述)、Franklin 和 Arthur Bernhart 发现了这些构型。
关于 Birkhoff 给出的三个候选项,研究人员的分歧很大,支持第一种选择的 Moore 给出了一种构造不可约构型的方法,其在 $20$ 世纪 $60$ 年代末之前就已发表。特别是 $1977$ 年 $3$ 月,他构造了一个由 $846$ 个多边形的地图,其中不包含可约的大小为 $11$ 及以下的环(但是,其包含一个可约的 12-环的构型)。这一结果表型,Birkhoff 的第二个候选项不能得到一个合理长度的证明,因为其至少要讨论 12-环的情形,这可能将包含大量的环构型。
另一方面,Heesch [16] 观察到,如果考虑尺寸不是很小且包含许多五边形的构型,就能得到很多的可约构型。他通过推测有限不可避免集合中可约构型将考虑到某个多边形的第二邻域将 Birkhoff 的第二个候选项表述为一个猜想 [16; p. 216]。Heesch 用平面三角剖分和顶点着色的对偶语言描述了他的结果,并用一种特殊编码表示顶点的度数(我们在本文中也用)。大约 $1950$ 年,Heesch 陈述了他的推测。
在 [16] 中 Heesch 处理了三角剖分的几个特殊情况,并证明了它们中的每一个都包含可约构型。在没有 $6,7$ 度的顶点的三角剖分的情况(Chojnacki [11] 早些时候用不同的方法处理过)下使用我们称为放电过程的方法解决。每个 $5$ 度顶点都包含 $60$ 个正数“电荷”且对于所有度数 $k\ge7$ 的顶点都含有 $60(6-k)$ 的负数“电荷”,根据 $(1.2)$ 我们可以得出总电荷量为 $720$。在“第一步放电”中,每个 $5$ 度的顶点都将其电荷均分到 major 相邻顶点中(major 指度数 $k\ge7$),然后可以证明,只有 $16$ 种特殊情况会产生正数电荷,前提是这个三角剖分不包含 $20$ 种可约构型中的一种。这 $16$ 种特殊情况中的每一种由一个构型来描述,其中一个 major 顶点从它度为 $5$ 的相邻顶点那里接收了如此多的正电荷,以至于它的电荷(最初是负的)有一个整数值 $z>0$。这些构型被称为 $z$-positive 构型,并且它们是不可约的(也不包含任何可约的子构型)。然后在“第二步放电”时,所有新的正电荷 $z$ 被分配到所有带负电荷的相邻顶点,并且保证没有正电荷剩余,当然保证了三角剖分不包含 $20$ 种可约构型。这意味着对于每个三角剖分的所有 $6,7$ 度的顶点都包含与 $20$ 个可约构型中(因为所有电荷的总和必须是正的)。
Haken 在 Heesch 报告时是 Kiel 大学的学生,$1967$ 年,他与 Heesch 进行了沟通,询问了证明 Heesch 的猜想的项目的技术难点,以及使用更强大的电子计算机的可能。
$1970$ 年,Heesch 向 Haken 传递了一个未发表的结果,他后来将其称为四色问题的有限化,即第一步放电(将在下面描述),如果应用于一般情况,会产生大约 $8900$ 个 $z$-positive 构型(其中大多数不包含任何可约构型),他明确展示了这一结果。他希望能够找到一组相对较大的可约构型,并算出第二步放电,以获得一个仅由可约构型构成的不可避免集合,从而证明四色猜想。Haken 对这项任务的复杂度非常悲观。他建议寻找更好的放电过程,以降低任务的复杂度。回到没有 $6$ 度顶点和 $7$ 度顶点的三角剖分的特殊情况,Haken 立即发现了放电过程的改进,大大缩短了该情况的处理时间 [15]。受到这一结果的鼓舞,Haken 提出了几项建议,为一般情况制定同样改进的放电过程。
Heesch 要求 Haken 与他合作,并于 $1971$ 年向他传递了关于可约构型的几个未发表的结果,特别是他对三个“可约障碍”的观察,称为 4-legger 顶点(即构型中的顶点且有四个及以上的相邻顶点在环绕着构型的环中),3-legger articulation 顶点(articulation 顶点就是割点)和 hanging 5-5-pairs(一对相邻的 $5$ 度顶点,仅通过边连接到构型中其他一个顶点)。其中一个障碍的存在似乎会阻止构型的可约性(除非构型包含可约且不包含障碍的正确的子构型)。
$1971$ 年 $10$ 月,当 Shimamoto 的工作被认为解决了四色问题时,Heesch 和 Haken 之间的合作中断了。实际上,Shimamoto 的工作诱导了 Tutte 和 Whitney 在 [27] 中第一个发表可约障碍理论。Stromquist [26] 随后使用了他们的方法,展示了几种进一步的可约障碍,其中包括上述三种类型,作为实际上最重要的特殊情况。
早在 $1972$ 年,Haken 就提出,作为证明 Heesch 的猜想的第一步,开发一种放电过程,该过程将产生一组不可避免的构型,这些构型不包含上述前两个还原障碍。这样的构型被称为 geographically good 的。目的是将重点从计算可约构型转移到改进放电过程,并获得最终证明所需的可还原构型的数量和大小的可靠估计。Osgood [24] 立即在这个方向上进行了研究,他处理了三角剖分的特殊情况,其中每个顶点度数都是 $5,6,8$。
Osgood 的工作的复杂度使 Haken 相信,即使我们有进一步改善的放电过程法,如果没有电子计算机,一般情况也无法有效地解决,因为电子计算机需要讨论所有可能的构型,这些构型可以通过合并给定构型的对、三元组等获得。很明显,如果一个人必须检查两次、三次或更多次“过度充电”(即使以前的负顶点为正)的 major 顶点的所有情况,那么这个任务就会反复出现。
此时,$1972$ 年 $5$ 月,Appel 建议继续进行该项目,因为他认为必要的计算机工作是完全可行的。
从 $1972$ 年到 $1975$ 年,Appel 和 Haken 逐渐改进了放电过程。放电过程可能有三种类型的主要缺陷:(i) 在某些情况下,正电荷可能会停留且不出现可约(或至少可能是可约)构型;(ii) 保留正电荷的本质不同情况的数量过多(在这种情况下,如果两种情况不产生相同的可约构型,则两种情况本质不同);(iii) 在保留正电荷的某些情况下,即使是最小的可约(或可能是可约)构型也具有过大的环尺寸。
手动搜索主要缺陷通常非常乏味(除非缺陷非常明显),但可以通过计算机非常有效地完成,计算机可以列举剩余正电荷的某些情况,并测试每个情况的可接受子构型(即,可能是可约的或至少是有限环尺寸的 geographically good 构型)。这种计算机程序的一个例子在 [4, Section 27] 中有更详细的描述。当发现主要缺陷时,我们必须找到一种方法来改变放电过程以避免缺陷。然后,通常情况下,计算机程序必须进行相应的更改,然后才能开始查找进一步的缺陷。
$1974$ 年,Apple 和 Haken 可以证明 geographically good 的构型 [4] 的有限的不可避免集合的存在,并描述了构造此类集合的算法。不久后,Stromquist [26, Chapter 4] 发现了一个更短的存在性证明(但没有构造算法)。[4] 的放电算法相当复杂,稍后通过将其应用于 [3] 中“孤立的 $5$ 个顶点”的特殊情况来说明;它在一般情况下的应用从未得到充分解决,因为在 $1975$ 年期间发现了更多的改进。
然而,$1972$ 年后,与 Heesch 的合作并未恢复,对于哪种处理一般情况的方法更好,双方无法达成共识。
到 $1975$ 年 $9$ 月,Appel 和 Haken 已经改进了迄今为止的算法,在每次新的改进之后,改变计算机程序似乎比手工进行缺陷计数更容易。此时他们决定,最有效的方法是手动进行放电算法,并将计算机工作转移到第二部分所述的可约构型的计算。(实际上,Appel, Haken 和 John Koch 在 $1974$ 年末就开始研究计算机的可约性算法。最初,他们推测,对于预期的大量大尺寸配置,需要不同于标准算法的算法,但放电算法的效率使得这是不必要的)。
$1976$ 年 $1$ 月,Jean Mayer 找到了一个处理孤立 $5$ 度顶点的可考虑的改进。几周前,作者找到了他们处理一般情况下的程序的相应的改进。将不同的放电过程应用于同一特殊情况并进行比较似乎很有意思。因此,作者将他们的放电过程(基本上与本文中使用的放电过程相同)应用于孤立 $5$ 度顶点的情况,并接受了 Mayer 的邀请,撰写了一篇联合论文 [5]。Mayer 的放电过程仍然比作者的放电过程简单有效得多,但到目前为止,还没有发现对一般情况的相应简化。然而,作者意识到在不同方向上可能会有某些改进;这些将在本文的第 5 节中进行讨论。
通过考察 Ore & Stemple [23]、Stromquist [26, Appendix] 和 Mayer [22] 关于 Birkhoff 数(用顶点数上限处理三角剖分)以及 Stanik [25] 和 Allaire [1](关于没有 $6$ 度顶点的三角剖分)的工作,可以对不同放电算法进行其他有趣的比较。
## 2. 放电过程
我们考虑一个二维闭流形 $M^2$ 的三角剖分 $\Delta$ 且具有欧拉示性数 $\chi$,我们假设 $\Delta$ 是一个单纯复形,即其不包含自环、$2$ 元回路、$3$ 元回路(三角形的三条边不算),此外,我们假设 $\Delta$ 的所有顶点 $V$ 满足 $\deg(V)\ge5$。
对于每个 $\Delta$ 的顶点 $V$ 我们给定一个初始电量 $q_0(V)=60(6-\deg(V))$,那么,根据 Kempe 给出的等式,我们有:
$$\sum_{V\in\Delta}q_0(V)=360\chi\quad(2.1)$$
注意到 $q_0(V_k)$ 对于所有 major 顶点($k\ge7$)都是负数,对于度为 $6$ 的顶点为 $0$,对于度为 $5$ 的顶点为正。
我们将主要通过图形(有界、平面、连接、简单连接的三角剖分)描述构型 $G$,其中顶点的 degree specifications 由 Heesch 引入的符号表示(见图 $1$)。如果存在符合 degree specifications 的单形浸入 $f:C\to\Delta$,则称构型 $C$ 包含在 $\Delta$ 中。这里我们使用以下定义。
我们称连续映射 $f:C\to\Delta$,将一个构型 $C$ 映射到一个三角剖分 $\Delta$,是一个浸入 / _immersion_(满足 degree specifications)如果其满足如下三个性质。

(i) $f$ 是 _simplicial_ 且 _dimension-preserving_ 的;即,如果 $\sigma$ 是一个 $C$ 的单形(顶点、边或者三角形)那么 $f\mid\sigma$ 是一个到 $\Delta$ 的(与 $\sigma$ 相同维度的)单形 $\sigma'$ 的同胚。
(ii) $f$ _满足 $C$ 的 degree specifications_;即,如果 $V$ 是 $C$ 的一个顶点且其度数被完全或部分确定(例如,$\deg(V)=6$ 或者 $\deg(V)\ge7$)那么 $\Delta$ 中的 $f(V)$ 也满足这个要求。
(iii) 平面中存在 $C$ 的一个小邻域 $N$ 满足 $N$ 是一个圆盘(即便 $C$ 可能有割点)且存在一个 _局部一对一的_ 扩张 $\tilde f$;即,如果 $N$ 是 $p$ 的一个点,且 $U$ 是 $p$ 在 $N$ 中的一个小邻域,那么 $\tilde f\mid U$ 是一个同胚。
如果两个构型 $C,D$ 满足存在一个单形浸入 $f:C\to D$ 遵循 degree specifications,我们就称 $C$ 包含 $D$。但是,在我们必须在本文中明确考虑的所有情况下,构型 $C$ 和 $D$ 将如此之小,以至于浸入 $f$ 将是嵌入(即,一对一,而不仅仅是局部一对一),并且 $C$ 将被称为包含在 $D$ 中作为子构型。
通常情况下,浸入或嵌入 $f$ 可以保持或反转 $C$ 的取向;特别是,如果 $C$ 和 $D$ 由平面中的图形定义,我们可能想区分 $C$ 包含在 $D$ 中反射或不反射的情况,或者不区分;如果我们想说 $C$ 的反射包含在 $D$ 中(即 $C$ 的镜像包含在 $D$ 中),那么我们写“$Cr$ 包含在 $D$”。表达式“ $C$ 包含在 $D$ 中”表示 $Cn$ 或 $Cr$ 包含在 $D$ 中。
现在我们将定义一个放电过程 $\mathscr P$,该过程可以应用于具有上述性质的任何三角剖分 $\Delta$,并为 $\Delta$ 的每个顶点 $V$ 分配终端电荷 $q(V)$,以便再次满足:
$$\sum_{V\in\Delta}q(V)=360\chi\quad(2.2)$$
我们在 $\Delta$(的顶点集合)上定义电荷函数 $q_0$ 通过将每个 $5$ 度顶点 $V_5$ 的电荷分给相邻的 major 顶点。我们区分了两种这样的电荷转移:(i) 短距离放电,其沿着将 $V_5$ 连接到 major 顶点的 $\Delta$ 的边缘转移电荷,以及 (ii) 横向放电,其将电荷从 $V_5$ 通过一个、两个或三个 $6-6$ 边(连接一对 $6$ 度顶点的边)转移到 major 顶点;缩写为 T-放电。首先,我们定义 T-放电,如果下面七个构型(我们称之为 T-放电情况)
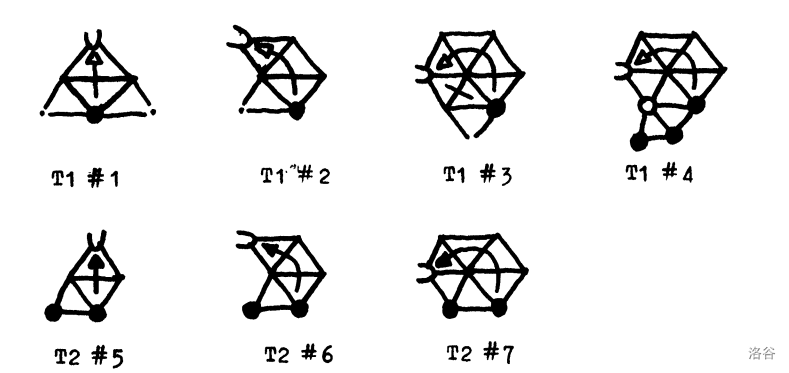
中的其中一个包含在 $\Delta$ 中,那么电荷按照图示的箭头转移。

实心箭头表示转移 $20$ 的电荷,空心箭头表示转移 $10$ 的箭头,但以下情况除外(见图 $3$):两个 T-放电从一个相同的 $V_5$ 跨过相同的 $6-6$ 边(但到达不同的 major 顶点)。如果这两个箭头中的至少一个是实心的,那么每个箭头将会只转移 $10$ 的电荷,否则,每个箭头只转移 $5$ 的电荷。在这种情况下我们用一个实心箭头分割为两个空心箭头或者一个空心箭头分割为两个转移 $5$ 电荷的骨架箭头,如图 $3$ 所示。
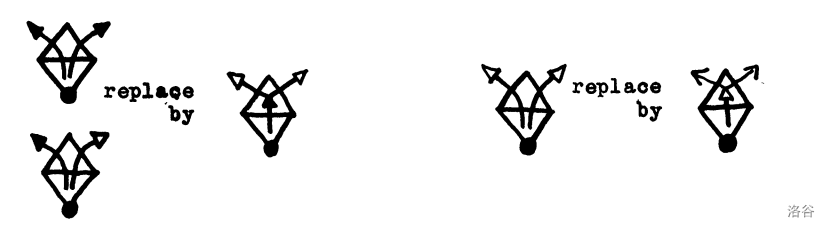
我们称一个转移 $5$ 或 $10$ 的 T-放电箭头为 T1-放电,转移 $20$ 的为 T2-放电(相应地,我们将图 $2$ 中的七种 T-情况命名为 T1#1, T1#2, T1#3, T1#4, T2#5, T2#6, T2#7)。偶尔我们会画一个无头箭头来表示一个 T-放电的路径但是我们不选择确定其转移的电荷数。举个例子,在 T1#3 的构型中,未指明的 T-放电在未指明度数的顶点(在图中的最底下)是一个($\Delta$ 的)$V_5$,那么该 T-放电就是 T2-放电,否则该 T-放电就是 T1-放电。
为了定义短距离放电,设 $E$ 是 $\Delta$ 的一条连接一个 $5$ 度顶点 $V_5$ 和一个 major 顶点 $V_k(k\ge7)$ 的边。在表 $1$ 中我们(用独特的图)已经定义了“小放电情况”,简写为 S-情况。大多数表 $1$ 的构型都包含一些部分指明度数($\ge6$ 或 $\ge7$)的顶点,用“裁剪标记”从构型中区分开。

除去这些被“裁剪”的顶点的构型是 S-情况。完整的构型被称为扩展 S-构型并且会在接下来解释(第 $3$ 节的引理 $S^+$)。这些构型的每一个都有一条 distinguished edge,它们都被垂直绘制,并且用一个数字标记($0,5,10,15,20,25$),这是它的放电量。我们说一个 S-情况 $C$ 应用于 $E$ 当且仅当 $C$ 被包含在 $\Delta$ 中且 $C$ 中的重要边 $D$ 被映射到 $E$。“大放电情况”,缩写为 L-情况,已经由表 $2$ 中的类似图形定义。同样地,放电数值($35,40,50,60$)已经被标记在重要边上了。
在图形中,我们使用了以下特殊缩略符号,如图 $4$ 中的示例所示。
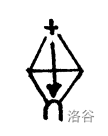表示一些附加的 T2-情况来表明一个带有 $20$ 电荷的 T-放电按照箭头方向到达一个 major 顶点。
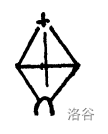表示一些附加的 T-情况(T1 或者 T2)来引起一个如箭头所示的 T-放电。
表示一个 major 顶点 $V$,除了一种情形:$V$ 不能是一个连接了 $V_5$ 的 $V_7$,其中,这个 $V_5$ 需要不属于这个构型但是需要与该构型的另一个顶点相邻。
表示一个 major 顶点 $V$,但是不能出现在右边的局部图中的点 $V$ 处。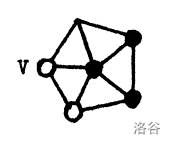
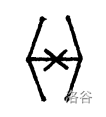表示没有 T-放电穿过这条标记的 $6-6$ 边。
现在关于一条边 $E$ 我们有三种情况(图 $5$ 有几个例子):
1. $E$ 既不是 S-情况也不是 L-情况,在这种情况下,我们称 $E$ 为 _规则放电边_ 或 R-边,我们将 $E$ 的放电值 $d(E)$ 定义为 $30$。
2. $E$ 从属于一个或多个 S-情况,但是不是 L-情况,那么我们称 $E$ 为 _小放电边_ 或 S-边,我们将其放电值 $d(E)$ 定义为等于从属的 S-情况下的最小放电值。
3. $E$ 从属于一个或多个 L-情况,那么我们称 $E$ 为 _大放电边_ 或 L-边,我们定义 $d(E)$ 等于从属的 L-情形的放电值中的最大值。
现在,将 $V_5$ 连接到 major 顶点 $A$ 的每条边 $E$ 具有唯一定义的放电值 $d(E)$(对于所有其他边,我们可以将放电值设为零)。我们通过(同时)沿每条边 $E$ 传输电荷 $d(E)$(从 $V_5$ 到 major 顶点)并执行 T-放电,从 $q_0$ 获得电荷分布 $q$。我们分别称沿 R-, S- 和 L-边的电荷转移为 R-, S- 或 L-放电。这样就完成了放电过程 $\mathscr P$ 的定义。
这是图 $4$:
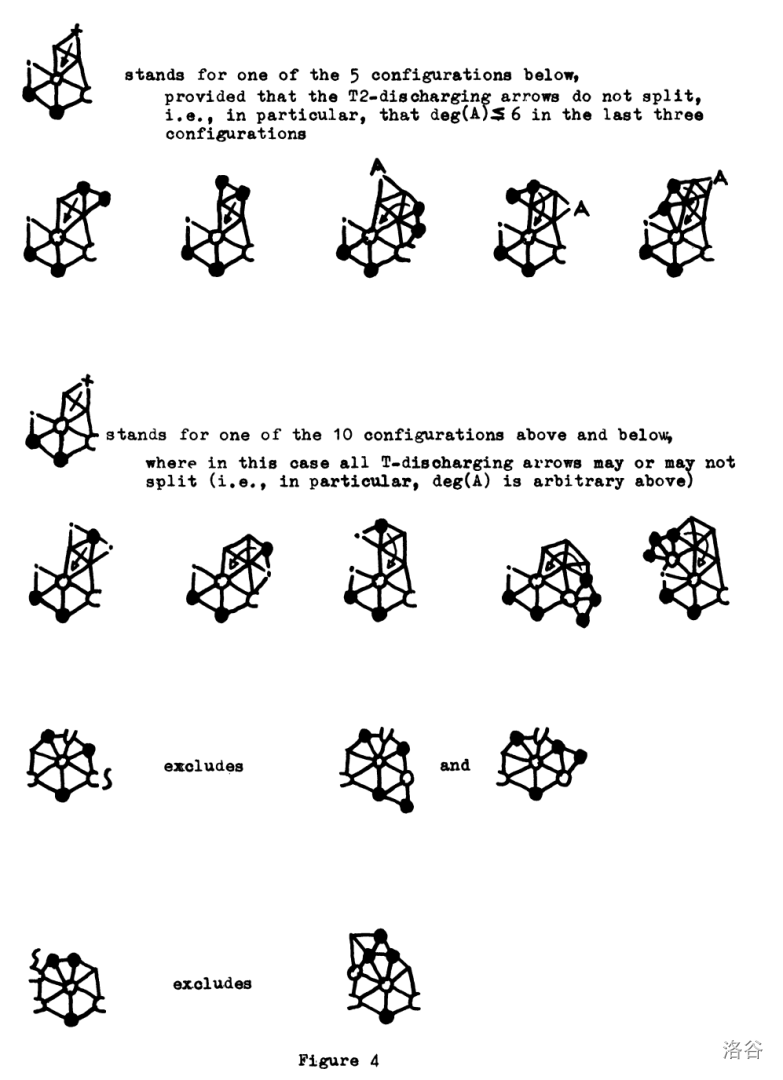
图片中英文翻译(从上到下):
1. 表示如下五种构型的一种,在所有情况中只要 T2-放电箭头不分离,即,特别地,在最后三种构型里,$\deg(A)\le6$。
2. 表示上下十种构型的一种,在所有情况中所有 T-放电箭头分离或不分离(即,特别地,在上面的 $\deg(A)$ 是任意的)。
excludes 意为排除,不包括。
这是图 $5$:
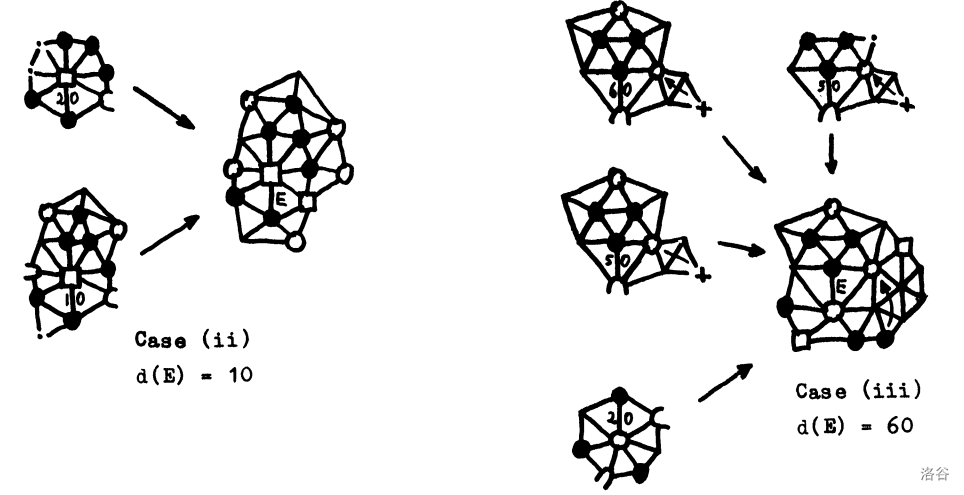
注意,放电过程基本上取决于图 $2$ 中定义的 T-放电情况集合 $\mathscr T$、S-放电情况集合 $\mathscr S$ 和表 $1,2$ 中定义的 L-放电情况集合。因此,准确地说,我们应该用 $\mathscr P(\mathscr T,\mathscr S,\mathscr L)$ 表示我们的放电过程,这表明我们将通过使用不同的 T-, S- 或 L-位置集合来获得不同的放电过程。
PS:远离 $\tt{\backslash mathscr}$,从你我做起。
我们注意到,$\mathscr S$ 中的大多数 S-情况( $269$ 个中的 $197$ 个)的放电值都是 $20$,而其余的大多数情况都是 $0$ 或 $10$。$0$ 在表 $1$ 中出现 $15$ 次($\#\#012,\dots,017,151,231,\dots,238$);$10$ 出现 $42$ 次($\#\#002,003,021,\dots,041,161,\dots,167,241,\dots,252$);$5$ 只出现一次($\#\#011$);$15$ 只出现一次($\#\#253$);$25$ 出现 $13$ 次($\#\#092,094,098,101,138,144,145,146,197,221,270,312,314$)。相应地,我们区分了三类 S-边,我们使用以下缩写:
+ $S0$ 表示放电值 $0$ 或 $5$。
+ $S1$ 表示放电值 $10$ 或 $15$。
+ $S2$ 表示放电值 $20$ 或 $25$。
在表 $1$ 中,我们根据以下区别对 S-情况进行了排序:
1. 与 distinguished edge 相连的两个顶点的度数(比如 $20\#001$ 的点 $A,B$),5-5 型仅出现一次($\#001$),$\#\#002,\dots,\#008$ 为 $5-6$ 型,没有 6-6 型,$\#\#011,\dots,150$ 是 5-major 型,$\#\#151,\dots,230.1$ 是 6-major 型,$\#\#231,\dots,329$ 是 major-major 型。
2. 放电值的类型 $S0,S1,S2$。
3. distinguished major 顶点的度($7,8,9$ 出现了,$9$ 只出现于 5-major 中)。
4. distinguished major 顶点的相邻顶点的度的字典顺序(逆时针方向阅读,从 distinguished $V_5$ 开始)。
关于 L-情况,我们使用以下缩写。
+ $L4$ 表示放电值 $35$ 或 $40$。
+ $L5$ 表示放电值 $50$。
+ $L6$ 表示放电值 $60$。
注意 $L5$ 仅出现了 $12$ 次($\#\#441,492,\dots,495,551,552,553,633,623,624,720$),$L6$ 仅出现了 $3$ 次($\#\#411,491,621$)。
在表 $2$ 中,我们根据以下区别对 L-情况进行了排序:
1. L-情况的宽度 $w$:pivot(distinguished major 顶点)的完全规定(fully specified)的相邻点的数量。$\#\#401,\dots,428$ 是 $W3$ 型($w=3$),$\#\#431,\dots,522$ 是 $W4$ 型($w=4$),$\#\#530,\dots,691$ 是 $W5$ 型,$\#\#701,\dots,730$ 是 $W6$ 型($w=6$ 或 $7$)。
2. L-情况的总放电值 $v$。通过这一点(By this),我们的意思是 $d(E)$(其中 $E$ 是 distinguished edge)之和再对每条从 pivot 到其它 $V_5$ 的边加上 $30$。在某些情况中($\#\#530,549,550,701,\dots,728$),L-情况包含另一个具有相同 pivot 但不同 distinguished edge 的 L-情况,称作 $F$,在这些情况中,$F$ 都是 $L5$,此时我们为 $F$ 加上 $50$ 而不是 $30$。例如,对于 $W5$ 型的构型有:
$$\begin{cases}\#530&v=120\\\#\#531,\dots,541&v=100\text{ or }95\\\#\#549,550&v=90\\\#\#551,\dots,553&v=80\\\#\#561,\dots,620&v=70\text{ or }65\\\#\#621&v=60\\\#\#622,\dots,624&v=50\\\#\#631,\dots,691&v=40\text{ or }35\end{cases}$$
## 3. 可约构型的集合 $\mathscr U
如果放电过程 \mathscr P(\mathscr T,\mathscr S,\mathscr L) 被应用于一个三角剖分 \Delta 上(如第二节所描述),那么可能会或者不会 完全放电 \Delta ,即,对于 \Delta 的所有顶点 V ,都有 q(V)\le0 ,现在设 \Delta^\ast 是一个不包含在本文第二部分中给出的 1834 个构型的集合 \mathscr U 中的任意一个构型的三角剖分,即,\Delta^\ast 避免了 \mathscr U ,我们会证明下述定理。
对于 \mathscr P(\mathscr T,\mathscr S,\mathscr L),\mathscr U 的放电定理:如果 \Delta^\ast 避免了 \mathscr U 那么 \mathscr P(\mathscr T,\mathscr S,\mathscr L) 完全放电 \Delta^\ast 。
关于 \mathscr U 中构型的数目:当这篇论文于 1976 年 7 月提交时,不可避免集合 \mathscr U 被宣布由 1936 种构型组成。从那时起,我们在 \mathscr U 中发现并消除了大约 100 个“冗余”,即意外列出两次的构型,或包含同样属于 \mathscr U 的适当子构型。此外,我们对本文进行了补充,该补充出现在缩微胶片上(见本期封底),并描述了的不可避免性证明的细节(即,如下所述的放电定理)。在准备这一补充时,我们发现了证明的一些简化,大致意思是并非 \mathscr U 的所有构型都是“真正需要的”,即 \mathscr U 的某个适当子集 \mathscr U' 也是不可避免的。然而,我们在本文中给出了完整的集合(仅从中删除了冗余,并对其进行了一些更正),因为我们认为这些构型的可约性可能本身就有一些意义。在第二部分的缩微胶片补充中,我们列出了 \mathscr U 中可以移除的 352 种构型,即属于 \mathscr U-\mathscr U' 的构型。因此 |\mathscr U'|=1482 。
如果 \Delta 的欧拉示性数 \chi 是正的,那么通过 (2.2) ,没有任何一个放电过程能够完全放电 \Delta ,且我们得到如下结果。
推论:如果 \chi>0 那么 \Delta 不能避免 \mathscr U ,特别地,任何(\chi=2 )的平面三角剖分都包含 \mathscr U 的至少一个元素。
因为 \mathscr U 的每个元素都是四色可约的(见第二部分),所以它不能被包含(即,浸入)在任何最小的 5-色平面三角剖分,这蕴含着 5-色平面三角剖分不存在,并且我们得出主要结论。
四色定理:任何平面三角剖分都是(顶点)可 4-着色的。
对于 \mathscr P(\mathscr T,\mathscr S,\mathscr L),\mathscr U 的放电定理的证明。由放电过程 \mathscr P 的定义可以立即得出对于 \Delta^\ast 中任意的 6 度顶点 V_6 都有 q(V_6)=0 ,那么这就相当于证明:
(A) q(V_5)\le0 对于 \Delta^\ast 中任意的 5 度顶点 V_5 。
(B) q(V_k)\le0 对于 \Delta^\ast 中任意的 major 顶点 V_k (k\ge7 )。
(A) 的证明。首先,我们证明一些关于 T-放电的一些初步的引理。
引理 (5-6-6) :如果一个 \Delta^\ast 的 5 度顶点 V 具有三个连续的度分别为 5,6,6 的相邻顶点,那么一个值为 20 的 T-放电会从 V 离开并穿过 6-6 边(如图 6 所示)。
证明:假设在任意一个三角剖分 \Delta 中,V 是一个具有三个连续的度分别为 5,6,6 的相邻顶点,使得没有 T2-放电离开 V (在 \Delta 中)穿过被称为 E 的 6-6 边。那么,根据 T-放电的定义,\Delta 中不包含 T2-情况 T2\#\#5,6,7 中的一种来引发一个从 V 穿过 E 的 T-放电。因此 \Delta 包含图 7 的四种构型中的一种,且包含图 7 中圈出的 \mathscr U 的四个成员之一。所以 \Delta\not=\Delta^\ast ,这证明了该引理。
引理 (6-6-6) :如果一个 \Delta^\ast 的 5 度顶点 V 有三个连续的度为 6 的相邻顶点,那么值至少为 10 的 T-放电会从 V 离开穿过每一个 6-6 边(见图 8 )。
引理 (5^5-7-6-6) :如果一个 \Delta^\ast 的 5 度顶点 V 有四个连续的度分别为 5,7,6,6 的相邻顶点使得另一个 V_5 与 5 度相邻顶点与 7 度相邻顶点都相邻,那么值至少为 10 的 T-放电会从 V 出发穿过 6-6 边(见图 9 )。
引理 (6-6) :如果一个 \Delta^\ast 的 5 度顶点 V 与一个 6-6 边 E 相邻使得没有 T-放电从 V 出发穿过 E 那么 \Delta^\ast 包含图 10 的构型(V,E 已在图中标记)。
引理 (6-6-6),(5^5-7-6-6),(6-6) 的证明与引理 (5-6-6) 是相似的(见微缩胶卷补充)。
引理 (S^+) :如果 f:S\to\Delta^\ast 是一个从 S-情况到 \Delta^\ast 的浸入(遵循 degree specifications),那么 f 可被扩展为一个从某个扩展 S-情况(如表 1 中所绘制)到 \Delta^\ast 的映射 f^+:S^+\to\Delta^\ast (使得 f^+ 仍然遵守 degree specifications)。
通过对表 1 (与第二部分的集合 \mathscr U )的检查,我们可以得出这是对的。
现在我们考虑放电过程 \mathscr P(\mathscr T,\mathscr S,\emptyset) (使用我们的 T- 和 S-情况,但没有 L-情况)并且我们用 q_{TS} 表示经过此过程获得的电荷分布,然后我们就有如下定理:
证明:这可以通过简单地枚举所有 $q_{TS}(V_5)>0$($V_5\in\Delta$)的所有可能情形证明($\Delta$ 如第二节中定义)。然后所有说明 $\mathscr U$ 中一个构型出现的情况被删除,其余情况都可以在表 $3$ 中找到。
我们记 $V$ 的 major 相邻顶点数量为 $\mu$,然后我们必须考虑 $\mu=0,1,2,3,4,5$ 的情况:
+ 如果 $\mu=0$,我们有 $V$ 被 minor 顶点包围,在任何情况下都会产生 $\mathscr U$ 的元素。
+ 如果 $\mu=1$,那么没有 $\mathscr U$ 元素出现的情况仅仅是 $CTS\#\#01,02,03$。在 $CTS\#\#01,02,03$ 中绘画的 T2-箭头表示由引理($5-6-6$)说明存在的 T-放电。
+ 如果 $\mu=2$,那么至少一个 S-情况必须存在 / must be attached(否则两个 R-放电会导致 $q_{TS}(V_5)\le0$);此外,如果只有一个 S-情况存在 / is attached,那么它的放电值 $d(E)$ 与引理($5-6-6$)($6-6-6$)($5^5-7-6-6$)所暗示的 T-放电的值之和必须小于 $30$(否则剩余 R-放电会导致 $q_{TS}(V)<0$)。这留下了情况 $CTS\#\#04,\dots,13$。
+ $\mu=3$ 的情况生成了最大的子情况树。在这个情况中,至少两个 S-情况必须存在且其中至少一个必须是 $S0$ 或 $S1$ 类型。不过如果放电值 $d(E)+d(F)$ 不小于 $30$ 那么第三个 S-情况必须存在。所有的不导致 $\mathscr U$ 中构型出现的情况包含了一个 $S0$ 情况或两个 $S1$ 情况。(列举子情况的所有组合细节都在本文的补充部分)。
+ $\mu=4$ 的情况下,两个 S-情况必须被附加在连续的边 $E,F$ 使得 $d(E)+d(F)<30$ 且 $E$ 是 minor-major 型但 $F$ 是 major-major 型。那么第三个 S 情况必须被附加在一条边 $G$ 上,并且如果 $d(E)+d(F)+d(G)\ge30$ 那么第四个 S-情况被要求存在。所有不导致 $\mathscr U$ 构型的情况都要么涉及两个 S0-情况和一个 S2-情况,要么涉及一个 S0-情况和两个 S1-情况。
+ 最后,如果 $\mu=5$,从 $V$ 出发的所有边都是 major-major 型的。首先考虑所有一个 S0 与一个 S0 或者 S1 的存在 / attachments 是方便的;只有几个不包含任何 $\mathscr U$ 中的构型。那么会发现所有连续的三元组 (S0, S0, S0), (S0, S0, S1), (S1, S0, S1) 都会生成 $\mathscr U$ 中的构型。那么枚举剩余的情况就是简单的;不包含 $\mathscr U$ 中构型的情况都包含四个连续的 S-情况,顺序为 S0, S1, S1, S0。$\quad\blacksquare
(A) 的证明将由以下内容完成。
L-引理:表 3 的每个构型 CTS\#\#01,\dots,33 (带有如表 3 所示的 S-情况)包含一个(表 2 的)L-情况附加到标记 X 的边且放电值足够大使得对于 central V_5 有 q(V)\le0 。
观察 / inspection 就能立即证明这一点。有关详细信息,请参阅第一部分的补充(提供于本期封底的缩微胶片)。在许多情况下,L-情况与表 3 的构型相同(有 S-情况存在)。\quad\blacksquare
(B) 的证明:我们再次通过一些引理开始,它们的证明是通过直接的枚举情况得到的。
引理 \text{(T)} :如果 V_k 是 \Delta^\ast 的一个与一条 6-6 边 E 相连的 major 顶点,那么 V_k 收到最多一个穿过 E 的 T-放电。
引理 \text{(T2, T2)} :如果 V_k 是 \Delta^\ast 的一个从两条连续的 6-6 边 E,F 收到 T2-放电的 major 顶点,那么图 11 两种构型的一种会被包含在 \Delta^\ast 中(且 V_k,E,F 如图 11 所示)。
引理 \text{(T2, T2, T2)} :如果 V_k 是 \Delta^\ast 的一个 major 顶点,那么 V_k 不会从三条连续的 6-6 边收到 T2-放电。
引理 \text{(T, T2, T2, T)} :如果一个 \Delta^\ast 的 major 顶点 V_k 从四条连续的 6-6 边 E,F,G,H 收到 T-放电,那么跨越第二、三条边 E,F 的放电不全是 T2-放电。
引理 \text{(60 OR 50, T)} :如果 \Delta^\ast 的一个 major 顶点 V_k 收到了穿过 X 的放电值为 50 或 60 的 L-放电,且收到了穿过与 X 紧邻(即 X 的 5 度顶点与 E 的 6 度顶点是连续的)的边 E 的 T-放电,那么如图 12 所示的 (a) 和 (b) 其中之一将会出现。
引理 \text{(60 OR 50, T2, T2)} :如果一个 \Delta^\ast 的 major 顶点 V_k 收到了一个放电值为 50 或 60 的 L-放电和一个穿过紧邻 X 的 6-6 边 E 的 T2-放电(见图 12a),那么 V_k 不能收到穿过与 E 连续的边 F 的第二个 T2-放电。
引理 \text{(60 OR 50, }\cdot\text{, 60 OR 50}) :如果 V_5^{(1)},V^{(2)},V_5^{(3)} 是 \Delta^\ast 的一个 major 顶点 V_k 的三个连续相邻顶点,且 V_k 从 V_5^{(1)},V_5^{(3)} 均收到一个 L6-放电 或 L5-放电,那么图 12 中 (c) (d) 两种情况中的一种会出现。
引理 \text{(5, L, }\cdot\text{, L, 5)} :如果 V_5^{(1)},V_5^{(2)},V^{(3)},V_5^{(4)},V_5^{(5)} 是 \Delta^\ast 的一个 major 顶点 V_k 的 5 个连续的相邻顶点,且 V_k 从 V_5^{(2)} 与 V_5^{(4)} 收到 L-放电(因此 V_5^{(1)},V_5^{(5)} 的度数为 5 ),那么图 12 中 (f) (g) (h) 中的一种将会出现(特别的,\deg(V^{(3)})=6 且 k\ge10 )。
引理 \text{(5, L, 5)} :如果 V_5^{(1)},V_5^{(2)},V_5^{(3)} 是 \Delta^\ast 中一个 major 顶点 V_k 的三个连续的 5 度相邻顶点,那么不会有 L-放电从第二个 5 度顶点 V_5^{(2)} 出发到达 V_k 。
引理 \text{(5, L)} :如果 V_5^{(1)},V_5^{(2)} 是 \Delta^\ast 中一个 major 顶点 V_k 的两个相邻的 5 度相邻顶点,那么没有 L5-放电和 L6-放电能够从 V_5^{(1)},V_5^{(2)} 出发到达 V_k (不过 L4-放电是有可能的)。
引理 \text{(5, L, T2)} :如果 V_5^{(1)},V_5^{(2)},V_6^{(3)},V_6^{(4)} 是 \Delta^\ast 中一个 major 顶点 V_k 的四个连续的相邻顶点,且有一个 L-放电从 V_5^{(2)} 出发到 V_k ,有一个 T2-放电穿过 V_6^{(3)} 与 V_6^{(4)} 间的边 E ,那么图 13 中的构型会出现(即,40#432 存在且 k\ge10 )。
引理 \text{(5, L, }\cdot\text{, 60 OR 50)} :如果 V_5^{(1)},V_5^{(2)},V^{(3)},V_5^{(4)} 是 \Delta^\ast 中一个 major 顶点 V_k 的四个连续的相邻顶点,且 V_k 收到一个从 V_5^{(2)} 出发的 L-放电,一个从 V_5^{(4)} 出发的 L6-放电或 L5-放电,那么从 V_5^{(4)} 出发的放电是 L-情况 50#441 诱导的(即,是 L5-放电)使得 \deg(V^{(3)})=7 。
引理 \text{(60 OR 50, T, 50 OR 60)} :如果 V_5^{(1)},V_6^{(2)},V_6^{(3)},V_5^{(4)} 是 \Delta^\ast 中一个 major 顶点 V_k 的四个连续的相邻顶点,且从 V_5^{(1)},V_5^{(4)} 都有一个放电值大于 40 的 L-放电到达 V_k ,穿过 V_6^{(2)},V_6^{(3)} 中间的边 E 有一个 T-放电到达 V_k ,那么 T1#1 附属于 E (并且 T-放电传输 10 个电荷到 V_k )。
上面的引理使我们能够计算所有到达 \Delta^\ast 的 major 顶点 V_k 放电之和的上界,我们将这个值记作 d(V_k) ,将相邻顶点中度数为 5 的顶点数量记作 v(V_k) 。
$$d(V_k)\le30k-7.5(k-v)\tag{3.1}$$
如果图 $13$ 的构型不出现(pivot 对应着 $V_k$)那么
$$d(V_k)\le30k-10(k-v)\tag{3.2}$$
证明:设 $V^{(1)},\cdots,V^{(k)}$ 为 $V_k$ 的相邻顶点(以顺时针顺序),我们给每个 $V^{(i)}$ 分配一个 _贡献值_ $c^{(i)}$ 使得
$$c^{(i)}=\begin{cases}30&\text{如果 }V^{(i)}\text{ 度数为 5}\\c_\ast^{(i)}+c_{\ast\ast}^{(i)}&\text{如果 }V^{(i)}\text{ 度数大于 5}\end{cases}$$
其中 $c_\ast^{(i)}$ 与 $c_{\ast\ast}^{(i)}$ 定义如下(下标对 $k$ 取模)。
PS:这里下标要对 $k$ 取模的话上面应该是 $V^{(0)},\cdots,V^{(k-1)}$。
(a) 如果 $V^{(j)}$ 是一个 $5$ 度顶点且从这个顶点有 L4-放电或 L5-放电或 L6-放电到达 $V_k$ 且 $V^{(j-1)},V^{(j+1)}$ 都不是 $5$ 度顶点,那么 $c_{\ast\ast}^{(j-1)}=c_{\ast\ast}^{(j+1)}$ 分别是 $5,10,15$,除了图 14 的三种情况,此时 $c_{\ast\ast}^{(j-1)},c_{\ast\ast}^{(j+1)}$ 如下面的图所示。
(b) 如果 $V^{(j)},V^{(j+1)}$ 都是 $5$ 度顶点,且从 $V^{(j)}$ 有 L4-放电到达 $V_k$,那么 $c_{\ast\ast}^{(j-1)}=10$。相对的,如果 $V^{(j-1)},V^{(j)}$ 是 $5$ 度顶点且从 $V^{(j)}$ 有 L-放电到达 $V_k$,那么 $c_{\ast\ast}^{(j+1)}=10$。
(c) 如果 $V^{(j)},V^{(j+1)}$ 都是 $6$ 度顶点,有 T1-放电穿过 $V^{(j)},V^{(j+1)}$ 中间的边 $E$ 到达 $V_k$,那么 $c_{\ast\ast}^{(j)}=c_{\ast\ast}^{(j+1)}=5$。
(d) 如果 $V^{(j)},V^{(j+1)}$ 都是 $6$ 度顶点,有 T2-放电穿过 $V^{(j)},V^{(j+1)}$ 中间的边 $E$ 到达 $V_k$,那么 $c_{\ast\ast}^{(j)}=c_{\ast\ast}^{(j+1)}=10$,除了图 15 的三种情况,此时 $c_{\ast\ast}^{(j)},c_{\ast\ast}^{(j+1)}$ 如下面的图所示。
(e) 如果对于某些 $i$,$c_\ast^{(i)},c_{\ast\ast}^{(i)}$ 并未由 (a) (b) (c) (d) 定义,那么其值为 $0$。
现在,由上面的引理我们有:
$$\sum_{i=1}^kc^{(i)}\ge d(V_k)\tag{3.3}$$
$$c^{(i)}\le\begin{cases}22.5&\text{如果 }V^{(i)}\text{ 不是 5 度顶点}\\20&\text{如果 }V^{(i)}\text{ 不是图 13 构型中的 5 度顶点或 6 度顶点}\end{cases}\tag{3.4}$$
这直接蕴含着 $(3.1),(3.2).\quad\blacksquare
推论(记号与上界引理证明中相同):如果图 13 中的构型不出现,且存在一个 l 满足 c^{(l)}<20 ,那么
d(V_k)\le30k-10(k-v)-10\tag{3.5}
证明:这可以从 (3.3),(3.4) 中得出,因为 \sum_{i=1}^kc_i 是 10 的整倍数。
现在对于所有 k\ge11 的顶点 V_k 证明 (B) 是简单的,利用事实
q(V_k)=d(V_k)-60(k-6)\tag{3.6}
如果 k\ge12 那么 (3.1),(3.6) 立即蕴含着 q(V_k)\le10 。如果 k=11 立即蕴含着如果 q(V_{11})>0 那么 v\ge8 ,但是如果 v\ge8 ,通过 (3.2) ,图 13 中的构型必须出现。另外一方面,v\ge10 的情况被从 \Delta^\ast 中排除了,因为 \mathcal U 中的 15-34。现在很容易检查在剩余情况中,q(V_{11})<0 或 15-34 或 15-35 出现。
还剩下对于 k=7,8,9,10 证明 (B)。
我们考虑放电过程 \mathscr P(\mathscr T,\emptyset,\mathscr L) (即,我们忽略 S-情况)并且我们定义对应的电荷函数 q_{TL} 。那么我们有:
这个引理可以通过直接对 $k=7,8,9,10$ 的枚举证明(见缩微胶片补充)。
对于 $k=7$ 我们必须考虑一个 $V_k$ 的这些相邻顶点情况:
+ (7.0) 没有 $5$ 度相邻顶点,但是有总放电值大于 $60$ 的 T-放电。
+ (7.1) 有一个 $5$ 度相邻顶点,从这个顶点出发有 R-放电或 L4-放电或 L5-放电或 L6-放电到达 $V_7$ 以及总放电值分别大于 $30,20,10,0$ 的 T-放电。
+ (7.2) 两个 $5$ 度相邻顶点与一个 T-放电或 L-放电。
+ (7.3) 三个或者更多的 $5$ 度相邻顶点。
表 4 列出了没有 $\mathscr U$ 中成员出现的情况。我们注意到所有宽度 $w\ge4$ 的 L-情况出现(即,除了前 $12$ 种情况的表 12)的情况都生成了可能是可约的构型,如果 pivot 是一个 $V_7$;但是这些构型中的一些具有大于 $14$ 的环尺寸。出于这个原因,我们倾向于将 $CTL\#\#76,77$ 的情况包括在表 4 中,而不是试图减少相应的长 $15$ 的环构型以将它们包括在 $\mathscr U$ 中。
对于 $k=8$,这种情况具有最大的组合复杂度,我们必须考虑下面的 $V_8$ 相邻顶点情况:
+ (8.1, 2, 3) 一个、两个或者三个 $5$ 度相邻顶点,与对应的强 T-放电 and/or L-放电。情况 (8.0),即,总放电值大于 $120$,可以被引理 $\text{(T), (T2, T2, T2), (T, T2, T2, T)}$ 排除。
+ (8.4) 四个 $5$ 度相邻顶点与一个 T-放电或 L-放电。
+ (8.5) 五个或者更多的 $5$ 度相邻顶点。
只有表 4 中的 $CTL\#138,139$ 包含宽度 $w\ge5$ 的 L -情况并且不产生 $\mathscr U$ 中的成员。
对于 $k=9,10$,$q_{TL}(V_k)>0$ 的结果是要求相当多的 $5$ 度相邻顶点使得要考虑情况的总数小于 $k=8$ 的情况。
S-引理:在表 4 中所有情况 $CTL\#\#1,\cdots,152$ 中,都出现了 S-情况(以表 1 的绘图展示),该 S-情况引起了如表 4 所示的小放电值使得每种情况中对于 central $V_k$ 有 $q(V_k)<0$(在某些情况下,S-情况可能导致比表 4 中所示更小的放电值)。
S-引理的证明可以通过观察立即得到。这就完成了 (B) 的证明,从而完成了放电定理的证明。
## 4. 概率性考虑
乍一看,Kempe 试图证明的四色猜想可以用这种可考虑的组合复杂性的方法来修复,而适度简单的修复似乎不太可能,这似乎是一个非常奇怪的意外。
这一节中,我们将提供一个基于概率论的初等(也是很粗糙的)应用,这导致我们相信,几乎一定存在一组不可避免的环大小 $n$ 不超过 $17$ 的可约构型,而且很可能存在一个环大小 $n\le14$ 的不可避免集合,而不太可能存在一个环尺寸 $n\le12$ 的这样的集合。只有对于 $n\le13$ 的集合,不能进行预测。
Edward F. Moore 在 $1977$ 年 $3$ 月构建的例子对 $n\le11$ 的存在性问题给出了否定回答,而本文对 $n\le14$ 的存在性问题进行了肯定解决,因此只有 $n\le12$ 和 $n\le13$ 悬而未解。虽然这篇论文可能会让许多数学家感到惊讶,但结合 Moore 的工作来看,它实际上表明没有什么令人惊讶的。因此,就目前而言,我们现在将概述的概率讨论似乎是对四色问题难度很大但有限的充分解释。
(a) 可约性的可能性。在下文中,我们将考虑 D-可约性(在 Heesch [16] 的意义中)作为我们的可约性标准。不熟悉 D-可约性的技术方面的读者将在 [16] [27] 中找到它们。虽然 C-可约性更强一点,但它似乎没有足够强来对于同一个 $n$ 改变结果,且其参数似乎更难定义。因此,在本小节中,可约将意味着 D-可约。
给定环大小为 $n$ 的构型 $C$,举个例子,$n=13$,我们可能会问“$C$ 有多大可能是可约的?”我们考虑围绕着 $C$ 的十三个顶点的环 $R$ 以及 $66,340$ 种不同的对 $R$ 着色的种类。这些着色有一个一个确定的百分比,成为 $x$,可以通过 $C$ 扩展,我们称这些着色为 initially good 或者 $\text{good}_0$。我们考虑 $R$ 的任意一种着色 $c$,且 $c$ 不是 $\text{good}_0$ 的,我们会问:通过一次简单的 Kempe 链论证,我们将这种着色转化为好着色的机会有多大?,即,$c$ 是 $\text{good}_1$ 的概率有多大(与 $\text{good}_0$ 着色集合的色距离为一)?
考虑将我们允许的四种颜色划分为两对的划分 $\pi$。这个环将可以根据这两对被分成 $2$ 颜色的连通分量,并且对应这两对的连通分量数是相同的(因为它们以顺时针顺序交替出现在 $R$ 上)。这个数量可能是 $1,2,3,4,5,6$,但是对于三个可能划分中的至少一个,对应于每一对的连通分量的数量必须是 $5$ 或 $6$,对于剩余两个划分中的至少一个划分,这数量必须至少为 $4$。我们将自己限制在生成 $R$ 的 $4,5,6$ 对 $2$ 颜色的连通分量的划分中。那么我们分别有 $7,15,31$ 种 Kempe interchanges 的选择让我们能够从 $c$ 得到一个 $R$ 的不同着色 $c'$。当我们考虑引出 $R$ 的着色 $c$ 的 $R$ 的外部的可能着色时,我们注意到,根据我们的划分 $\pi$ 在 $R$ 上有 $4,5,6$ 对连通分量,有 $14,42,132$ 种可能的 Kempe chain dispositions。如果对于 _所有_ 的 Kempe chain dispositions,_一些_ Kempe interchange 生成了一个 $\text{good}_0$ 着色 $c'$,那么 $c$ 是 $\text{good}_1$ 的。因为缺乏更好的可用信息,我们假设 $\text{good}_0$ 着色是随机分布在 $R$ 的所有着色中的,并且包含了可能着色的 $100x\%$。那么对于每个 Kempe chain dispositions,存在一些好 Kempe interchange 概率分别是:
$$\begin{matrix}y_4=[1-(1-x)^7]^{14}\\y_5=[1-(1-x)^{15}]^{42}\\y_6=[1-(1-x)^{31}]^{132}\end{matrix}\tag{4.1}$$
这些函数如图 16 所示。
图像表明,对于 $x<10\%$,Kempe chain 论证实际上没有成功的可能,对于 $x=20\%$ 就有非常好的成功率了,对于 $x=30\%$ 我们就可以期待可约性是必然的.例如,图 16\* 中的构型 (b) (c) (d),其中 $g$ 表示构型周围的环 $R$ 的 $\text{good}_0$ 着色的数量。构型 (b) (c) 有 $11.4\%$ 与 $12.1\%$ 的 $x$ 值,但它们都不是 D-可约的(但是是 C-可约的),并且 (d) 有 $14.6\%$ 的 $x$ 值是 D-可约的。
下面我们估计构型 $C$ 的顶点数(不包括环 $R$ 上的顶点)$m$ 与 $C$ 可约的可能性之间的函数关系。尽管对于给定的 $m$ 和 $n$ 估计 $x$ 的期望值不是那么容易,但是对于固定的 $n$,$x$ 的平均值将随着 $m$ 增加而迅速增加是非常合理的(因为 $C$ 的可能的着色的总数将随 $m$ 显著增加)。
> 按照如下方式,可以获得 $x$ 与参数 $n,m$ 的依赖性的合理估计。为了估计对 $n$ 的依赖性,我们将构型 $C$ 的顶点 $P$ 的度数提高一。用 $C_{n+1}$ 表示通如此获得的构型,例如,设 $C$ 和 $C_{n+1}$ 为图 16\* 中的 (a) 和 (b)。我们假设存在三角形 $ABP$,使得 $A,B$ 在围绕 $C$ 的环 $R$ 上(即,$P$ 至少是 $C$ 的 2-legger 顶点)。为了生成 $C_{n+1}$ 与围绕其的环 $R_{n+1}$,我们将环 $R$ 上的边 $AB$ 通过一个新顶点 $V$ 细分,对应地,将三角形 $ABP$ 通过一条连接 $V$ 与 $P$ 的边细分(一个 $P$ 的新 leg)。现在我们考虑 $R_{n+1}$ 的所有 $g_{n+1}$ 个 $\text{good}_0$ 着色,其中的每一个都扩展到 $C_{n+1}$。假设我们不知道 $C_{n+1}$ 的任何细节,我们可以估计有 $50\%$ 的概率,这些着色在 $A,B$ 具有相同的颜色。这些着色并不对应于 $R$ 的着色,其它着色有 $50\%$ 的概率(其中 $A,B$ 有不同的颜色)一一对应于 $R$ 的 $g$ 个 $\text{good}_0$ 着色,因此我们估计:
>
> $$g_{n+1}=2g_n,x_{n+1}=0.66x_n$$
>
> (注意,$R_{n+1}$ 的着色总数几乎恰好是 $R$ 的着色数的三倍)
>
> 为了估计 $x$ 与 $m$ 的相关性,我们向一个构型 $C$ 中加入一个新的环顶点 $V$ 并对 $V$ 给定一个 degree specification 以便生成一个构型,记为 $C_{m+1}$,具有与 $C$ 相同的 $n$ 值(在 [26] 中这个操作被称为 1-extension),例如,$C$ 与 $C_{m+1}$ 分别是图 16\* 中的 (c) 与 (d)。我们假设新顶点 $V$ 在 $C$ 中恰好有两个相邻顶点,称作 $P,Q$,因此在 $C_{m+1}$ 中具有 degree-specification $5$。在 $R_{m+1}$ 中一个新顶点,称作 $W$,取代了 $R$ 中的 $V$。现在我们考虑所有的 $g$ 个 $R$ 的 $\text{good}_0$ 着色,其中的每一个都扩展到 $C_{m+1}$。设顶点 $A,P,Q,B$ 以环绕 $V$ 的顺序排列。然后我们可以估计,在 $50\%$ 的着色中,顶点 $Q$ 的颜色不同于 $A$,而在这些着色中,$50\%$ 的顶点 $B$ 的颜色与 $A$ 相同。因此,在 $R$ 的所有 $\text{good}_0$ 着色中,有 $25\%$ 概率,$A,B$ 具有相同的颜色。对于这些着色中的每一个精确对应 $R_{m+1}$ 的两个 $\text{good}_0$ 的着色(在每种情况下 $W$ 有两种颜色选择),而 $A,B$ 不同颜色的那 $75\%$ 的着色与 $R_{m+1}$ 的着色一一对应。因此,我们可以预期 $g_{m+1}$ 比 $g$ 大 $25\%$。然而,如果 $c$ 是 $R$ 的 $\text{good}_0$ 着色,且 $A,B$ 具有相同的颜色,那么我们有 $2x\%$ 的可能性存在 $R$ 的另一种 $\text{good}_0$ 着色,称作 $c'$,它与除 $V$ 以外的 $R$ 的所有顶点上的 $c$ 一致。在这种情况下,我们只能将 $R_{m+1}$ 的三种不同的着色对应于两种着色 $c$ 和 $c'$。因此,我们可以估计 $g_{m+1}$ 将仅比 $g$ 大 $25(1-x)\%$。
>
> 现在,如果我们考虑两个构型 $C,C'$,我们能期待通过上述操作的序列(度提升和 1-extension)及其逆将 $C$ 变为 $C'$ 吗?如果我们假设 $C$和 $C'$ 不是明确的,那么在我们感兴趣的大多数情况下,答案将是“是”。然而,偶尔我们可能需要 1-extension,其中顶点 $V$ 恰好与 $C$ 的三个顶点相邻,并且相应地在 $C_{m+1}$ 中具有 degree-specification $6$。在这种情况下,$g$ 值的增加可以估计为 $37.5(1-x)\%$。
>
> 对于具有我们感兴趣的数量级的 $n,m$ 值的构型,我们现在可以估计,$n$ 增加 $1$ 会使 $x$ 减少 $33\%$,$m$ 增加 $1$ 会导致 $x$ 增加 $23\%$。这解释了经验观察,即(对于无可约障碍构型)可约性的可能性基本上取决于差值 $n-m$。如果 $n$ 和 $m$ 都增加 $1$,那么 $x$ 将减少约 $18\%$。这意味着,例如,具有 $8$ 个顶点的 $11$ 环构型将具有约为具有 $10$ 个顶点的 $13$ 环构型的 $x$ 值的 $1.5$ 倍的 $x$ 值。但对于 $n=11$,图 16 中的曲线 $y_5$ 和 $y$ 所起的作用与 $y_6$ 和 $y$ 在 $n=13$ 中所起的作用相同。因此,可以假设两种构型的可约性的可能性大致相同,13 环的可约性可能性可能略大于 11 环的构型。
基于此,我们可以预测将有一个“临界”值 $m'$,使得 $m>m'$ 意味着“可能可约”,而 $m<m'$ 意味“可能不可约”。当然,上述预测应利用我们所掌握的知识,并且应仅适用于不包含任何已知可约障碍(见 [26; Chapters II, III])的构型,因此特别应用于 geographically good 且没有 hanging pairs 的构型(参见本文 Section 1)。对于小的环尺寸,$n=6,\dots,11$,已经对这些构型进行了详尽的研究(F. Bernhart [8], Allaire & Swart [2], Koch [20])。这些结果建议“临界 $m$ 值”满足
$$m'=n-5\tag{4.2}$$
对于 $n=6,7,8,9$,所有没有可约障碍的构型都满足 $m>n-5$,并且它们都是 C-可约或者 D-可约的(注意 $5-5-5$ 三角形包含 hanging pairs,不包括在内)。对于 $n=10$,只有 $m=n-5=5$,$(7-5665)$ 这种构型是不可约的,而那些更大 $m$ 的构型是可约的(细心的读者会注意到,其中一些是 C-可约但不是 D-可约的,但绝大多数是 D-可约的。C-可约性似乎不会改变“临界值”这一事实本身就证明了使用 D-可约性的合理性)。
> 这里“不可约”的意思是 C-不可约。E. R. Swart 最近发现,由 Arthur Bernhart 提出的更强的可约方法可以用来证明构型 7-5665 是可约的。然而,就改进的可约方法而言,这里提到的可约障碍似乎仍然有效。
对于 $n=11$,存在 $6$个 构型满足 $m=n-5=6$,其中 $4$个构型是可约的;只有一种 $m>n-5$ 的构型不可约(8-556655,$m=n-4=7$)。基于此,对于 $n=12,13,14,\dots$,接受 $(4.2)$ 似乎是合理的,人们可能实际上期待对于一些更高的 $n$ 值,$m'=n-6$ 将是更合适的。到目前为止获得的计算机结果(见 [1] [9] [17] 和本文的 Part II)没有表明任何怀疑 $(4.2)$ 的理由。
在 [4] 中,作者引入了一个函数
$$\phi(C)=n-m-3\tag{4.3}$$
并证明了满足 $\phi(C)\le0$ 的任意构型 $C$ 总是包含 geographically good 的子构型,比如 $C^\ast$,且同样具有$\phi(C^\ast)\le0$。(证明是对 $m$ 的简单归纳)。但不幸的是,子构型 $C^\ast$ 可能仍然包含一个 hanging pairs,因此可能不“可能是可约的”。然而,我们有以下引理:
$m$ 引理:设 $C$ 是包含 $m$ 个顶点(在环内)的环大小为 $n$ 的任意构型,假设:
$$m>3n/2-6,\text{ 或者等价的, }\phi<3-n/2\tag{4.4}$$
则 $C$ 包含同样满足 $(4.4)$ 的子构型 $C^\ast$,使得 $C^\ast$ 在没有 hanging pairs 且 geographically good。此外,如果 $A$ 是 $C^\ast$ 的 articulation 顶点,且 $W_1$ 和 $W_2$ 是 $A$ 的两个“wing”(即,从 $C^\ast$ 中删除 $A$ 所得的两个构型)那么我们有:
$$\forall i=1,2:m(W_i)\ge3n(W_i)/2-6$$
证明:很容易验证 $m$ 不能为 $1,2,3$(因为我们已经排除了度小于 $5$ 的顶点),并且 $m=4$ 时唯一可能的 $C$ 是 Birkhoff 的可约 $5-555$ 双三角形;因此 $C^\ast=C$。现在通过归纳假设,引理适用于至多 $m-1$ 个顶点的所有构型。然后我们断言引理也适用于 $C$。如果 $C$ 具有 $C^\ast$ 所需的所有性质,那么我们让 $C^\ast=C$,证明就完成了。如果 $C$ 包含一个 4-legger(或者更大的数-legger)顶点 $V$,那么删除 $V$ 得到的构型 $C'$ 满足 $m(C')=m-1,n(C')\le n-1$,因此 $C'$ 满足 $(4.4)$,通过归纳假设需求的子构型 $C^\ast$ 可以在 $C'$ 中找到。
如果 $C$ 包含一个“坏” articulation 顶点 $B$,那么我们断言 $B$ 的 wings $C_1,\dots,C_k(k\ge2)$ 中存在至少一个满足 $(4.4)$,称作 $C_1$。那么通过归纳假设,$C_1$ 包含需求的 $C^\ast$。
考虑反证法,因此我们假设:
$$\forall i\in[1,k]:m(C_i)\le 3n(C_i)/2-6\tag{4.5}$$
更进一步,如果 $k=2$ 且 $B$ 是一个 2-legger 顶点,则对于两个 wings 中的至少一个,称作 $C_1$,有 $m(C_1)<3n(C_1)/2-6$。现在我们有
$$m=\sum_{i=1}^km(C_i)+1\tag{4.6}$$
$$n\ge\sum_{i=1}^k[n(C_i)-2]\tag{4.7}$$
其中 $(4.7)$ 中的等号成立,当且仅当 $B$ 是 k-legger 顶点(即,恰好一个“leg”位于每两个连续的 wings 之间)。将 $(4.6)$ 与 $(4.5),(4.7)$ 组合,我们有:
$$m\le\frac32\sum_{i=1}^k[n(C_i)-4]+1\le3n/2-3k+1$$
其中在 $k=2$ 的情况下,两个等号不能同时成立。但这与假设 $(4.4)$ 相矛盾;这就完成了证明。$\quad\blacksquare
通过上述引理,满足 (4.4) 的构型 C 不包含任何已知的可约障碍,并且可以被视为极有可能是可约的。(注意,它远远超过了我们前面给出的临界条件)我们可以推测,满足 (4.4) 的每个构型都是 D-可约的;但我们并不期待这个猜想能被证明。
(b) 不可避免性的可能性。对于一个给定的整数 n_0\ge5 ,我们可能会尝试找到整数 r 与 \phi_0 满足任何一个三角剖分(平面图且顶点度 \ge5 )包含至少一个 n\le n_0,\phi\le\phi_0 的构型包含于一个顶点的第 r 邻域中。Stromquist 的工作刺激了这个问题,他在 [26; Chapter IV] 中证明了每个三角剖分至少包含一个 \phi<-1 的构型,该构型包含在顶点的第二邻域中,并且其中没有顶点的度数大于 30 (从而证明了 geographically good 的构型的有限、不可避免的集合的存在性)。
我们在三角剖分中考虑以下“邻域的大小类”。
大小类
描述
1
单个顶点
2
边(一对相邻的顶点)
3
三角形(具有两个连续相邻顶点的顶点)
4
双三角形(具有三个连续相邻顶点的顶点)
5
三三角形(具有四个连续相邻顶点的顶点)
6
顶点的第一邻域(具有所有相邻顶点的顶点)
7
大小类 6 的邻域 N_6 加上一个三角形(以 N_6 作为基础)
8
一条边的第一邻域
9
一个三角形的第一邻域
\dots \dots
s 大小类 s-6 的邻域 N_{s-6} 的第一邻域(对于 s\ge8 )
\dots \dots
这些大小类中的每一个都有一个“平均 n ”和“平均 m ”(所有三角剖分中大小类的所有构型的平均值)。由于“平均顶点度”一定是 6 ,我们可以通过考虑(相应大小类的)仅由 6 度顶点组成的构型来大致了解这些平均值是什么。图 17 中绘制了相应的 b 值与 n 值,并用 \sf X 标记,大小类写在标记上方。从大小类 15 (n\ge21 )开始 \phi 值低于 \phi=3-n/2 线,因此这个大小类的平均构型几乎一定是 D-可约的(见 m 引理)。
当然,每个三角剖分都将包含每个大小类的一些构型,其 b 值低于平均值;对于通过 (1.2) ,每个三角剖分都必须包含度为 5 的顶点(即,度实际上低于平均值 6 )。为了估计这些“不可避免的 \phi 值”,我们考虑了不同大小类的构型,使 5 度顶点尽可能靠近中心,而所有其他顶点都是 6 度。结果如图 17 所示。从 n=17 开始,这些值处于 D-可约性的极高可能性的区域中。
另一方面,我们预期存在三角剖分,其中 n\le12 的所有构型的 b 值 \ge0 。因此,可以进一步预期,在其中一些三角剖分中,所有 n\le12 的构型都不可约。例如,所有构型可能都满足迭代删除 4-legger 顶点最终产生一个 V_5(\phi=1) 或一个 5-5-5 三角形(\phi=0 )。
类似地,我们预期存在三角剖分,其中所有 n\le13 的构型都有 \phi\ge-1 。但是,想象所有这些构型都是不可约的就不那么容易了。当然,在去除 hanging 5-5 pairs 和 4-legger 顶点之后,具有 \phi=-1 和 n=13 的构型可能不会产生比 5-5-5 三角形更好的结果,并且是不可约的;但是,是否存在三角剖分使得这种情况在所有情况下都发生似乎是不能进行合理预测的。n\le14,n\le15,n\le16 的相应的推理越来越倾向于认为每个三角剖分都将包含 n 范围内的可约构型。
5. 可能的改进
在求解本文给出的放电过程和不可避免集合 \mathscr U 时,我们从前面概率性考虑中得到了有效的指引。
我们一直拒绝接受任何 15 环构型作为不可避免集合的成员。每当我们没有比 15 (或更大)环构型更好的选择时,我们就会改变放电过程(通过改变 T-放电、S-放电和 L-放电情况的集合)。在大多数情况下,这些更改似乎减少了不可避免集合中的构型数量,并简化了证明。然而,在某些情况下,我们可能已经接受了超过十种 n<15 的构型,以替换一种 n=15 的构型。
另一方面,每当 n\le14 的构型出现时,如果我们发现它“易于机器可约”(即,在合理的时间长度内 D-可约,或使用我们程序可访问的类型的可约器 C-可约),我们就接受了它。我们知道,在许多情况下,更仔细的论证(甚至不改变放电算法)可能表明该构型实际上不是必需的(但可以由其他已经接受的构型替换)。见第 460 页脚注 4。
通过这种方式,我们提出了一个证明,这个证明肯定不是最好的,但在我们看来,“第一次尝试相当接近”最好的。
在这一点上,我们注意到,人们可以尝试从完全不同的方向“改进”证明。例如,可以尝试绝对最小化不可避免集合中的构型数量(可能以更复杂的放电过程、更大的环尺寸和所需的更多计算机时间为代价)。或者,可以尝试最小化构型的环尺寸(可能以增加构型数量为代价)。第三,可以尽可能简化手工完成的部分工作(以增加计算机完成的工作量为代价)。第四,无论是用计算机还是手工处理,都可以尽量减少证明的总组合复杂性。
如何合理地定义这类证明的总体复杂性似乎是一个有趣的问题。可以将其区分为逻辑复杂性和组合复杂性。
我们相信,我们的证明在逻辑上非常简单,所有的复杂性都是组合性质的。大约 485 种独立的 S-放电情况和 L-放电情况的数量相对较大,这使得逻辑简单的程序执行起来繁琐,因为必须考虑大量的情况。不可避免集合 \mathscr U 中的大量构型需要同样大量的可约性证明。同样,每一个可约性证明在逻辑上都很简单,但需要处理很多不同的着色,对于这些着色中的许多着色,需要处理大量的 Kempe chain arguments。
可以将可约性证明(对于单个构型 C )的组合复杂性定义为所需的那些 \text{good}_0 着色的数量和所有为 \text{good}_k(k>0) 的所需着色的数量之和,这些着色中的每一个乘以所需的不同 Kempe interchanges 的数量,以便将其与 \text{good}_{k+1} 着色相关联(在 Kempe chain 构型的所有可能情况下)。
应用这个概念,13 环构型的 D-可约性的证明将具有远超 106 的复杂性,而使用特别合适的可约器的 C-可约性证明可能具有低于 104 的复杂性,在非常好的情况下甚至低于 103 的复杂性。尽管现在的计算机完全能够计算 D-可约性,但人们可以考虑让计算机搜索它能找到的最好的 C-可约性(即使构型是 D-可约的),然后选择它能找到最短的 C-可约性证明。在许多情况下,这种证明可以通过合理的努力进行手工检查。
然后,整个证明的总组合复杂性将是所需的所有可约性证明的复杂性的总和(加上不可避免性证明所需的事例区分的数量,然而,可以预期其远小于可约性证明的复杂性)。我们认为,获得证明四色定理所需的最小组合复杂度的合理好的估计是有趣的。
放电过程的选择可以被视为一系列主要决定的结果,这些决定必须在其他常规程序的某些阶段做出。我们从极简单的放电过程 \mathscr P(\emptyset,\emptyset,\emptyset) (见 Section 3)开始,并将对应的电荷函数称作 q_R (q_R 从 q_0 中通过每条 5-major 边“正规”放电,放电值为 30 )。这产生了一个相对较小的构型列表,称为 q_R -positive 构型。其中一些包含可约子构型,其成为将由该过程构造的不可避免集合 \mathscr U 的成员。剩下的 q_R -positive 构型称为临界构型。
如果我们已经为了 \tilde U 从每个包含一个可约子构型的 q_R -positive 构型中接受了一个可约子构型,那么此时的临界构型将是 CTS\#\#01,02,03 (表 3 中删除箭头的构型),以及
一张无编号的图。
以及 CTL\#\#1,\dots,22,28,\dots,36,81,\dots,90 与 141 (表 4 中删除箭头的构型)。
此时,做出了第一个主要决定;我们必须选择在 \mathscr P 中使用的“长距离放电”。在本文中,我们选择了七种 T-放电情况的集合 \mathscr T (图 2);但人们可以尝试其他选择。现在已经定义了放电过程 \mathscr P(\mathscr T,\emptyset,\emptyset) 和相应的电荷函数 q_R 。一旦以这种方式选择了 \mathscr T ,上面绘制的两个 q_R -positive 构型就不再是 q_R -positive 构型;但另一方面,我们必须将构型 CTL\#\#11,12\text{(带箭头)},23,\dots,27,37,\dots,55,91,\dots,94 (来自表 4)添加到临界 q_R -positive 构型的集合中。
现在,我们的第二个主要决定是选择要使用的小放电情况,以便在上述临界 [q_T(V_k)>0,k\ge7] 的情况下避免 major 顶点 V_k 处的正电荷。这个决定是通过指定一组“primary S-放电情况” \mathscr S_0 来做出的(在本文中,表中大约 70 个成员是这个意义上的 primary 成员)。\mathscr S_0 的选择生成了一个放电过程 \mathscr P(\mathscr T,\mathscr S_0,\emptyset) 与对应的放电函数 q_{TS_0} 。当然,我们已经做出了一个基本的决定,即哪些可约构型应该被允许进入 \tilde U (在本文中,任何 15 环构型都不被允许。相反,人们可能只允许在某种意义上容易还原的构型;但这个决定取决于人们心中的目标)。
接下来,列举所有临界 q_{TS_0} -positive 构型是一个纯粹的机械过程。然后,我们必须决定使用哪些大放电情况,以避免在这些临界构型的 central V_5 顶点处产生正电荷。在大多数情况下,这一决定是“自动的”(在我们使用的程序中,它在 所有 情况下都是自动的)。这是由于最多一条 V_5 -to-major 边满足留下一个 q_{TS_0} -positive V_5 且不是 S_0 边,并且这种边是 L-放电边的自然选择。对 L-放电情况集合 \mathscr L_0 的选择将会生成 \mathscr P(\mathscr T,\mathscr S_0,\mathscr L_0) 与 q_{TS_0L_0} 。此时,必须选择额外的 S-情况,以关注临界 q_{TS_0L_0} -positive major 顶点。这生成一个扩大的集合 \mathscr S_1(\mathscr S_0\subset\mathscr S_1),\mathscr P(\mathscr T,\mathscr S_1,\mathscr L_0) 以及 q_{TS_1L_0} 。这个过程不断迭代,直到在某个阶段,没有出现任何临界 positive 情况。然后完成了放电过程和不可避免集的构造(对于本文中提出的放电程序,我们需要三个附加 S-情况与 L-情况的阶段,\mathscr S=\mathscr S_3,\mathscr L=\mathscr L_3 ,其中 \mathscr L_3 仅由 \mathscr L_2 添加两个元素得到)。
有趣的是,问为什么如果决策是“合理的”,这个过程“必须”终止。对从一个阶段到另一个阶段的观察可以得到答案,即临界 positive 构型中 positive contral 顶点包含越来越多的非 5 度相邻顶点。
我们没有进行任何上述类型的进一步实验,因为如果手动进行,临界 positive 构型的纯机械枚举过程相当耗时。当然,由于枚举过程在逻辑上非常简单,因此可以编写计算机程序来执行。然后,手工完成的工作将包括做出上述重大决策,并且不会涉及太多工作。但在这样一个自动化的阶段,应该如何定义程序的改进?
在目前的发展阶段,许多数学家可能更喜欢用机器进行约简证明的方法,而其他一切都是手工完成的。实现这一目的的最好方法可能是详尽地计算长 12 与 13 的环(与 Allaire & Swart 在 [2] 中处理长 10 的环和在尚未发表的工作中处理长 11 的环的方式相同)。这将处理组合工作中最乏味的部分。生成一个构型比检查这个构型是否包含一个属于给定的可约构型的大集合 \mathscr U 的可约子构型要容易得多。但是,很容易验证一个构型是否包含一个子构型满足 n\le13 ,与比如说 \phi\le1 。如果这件已经完成了,只需要列出 n\le13 的少数不可约构型和 n=14 所需的可约构型(后者的数量肯定会比我们的集合 \mathscr U 中的大约 660 个小得多)。
参考文献
F. ALLAIRE, A minimal 5-chromatic planar graph contains a 6-valent vertex , to appear.
F. ALLAIRE AND E. R. SWART, A systematic approach to the determination of reducible configurations in the four-color conjecture , J. Combinatorial Theory (B), to appear.
K. APPEL AND W. HAKEN, An unavoidable set of configurations in planar triangulations , J. Combinatorial Theory (B), to appear.
——, The existence of unavoidable sets of geographically good configurations , Illinois J. Math., vol. 20 (1976), pp. 218-297.
K. APPEL, W. HAKEN, AND J. MAYER, _Triangulations à v_5 séparés dans le problème des quatre couleurs_, J. Combinatorial Theory (B), to appear.
A. BERNART, Six rings in minimal five color maps , Amer. J. Math., vol. 69 (1947), pp. 391-412.
——, Another reducible edge configuration , Amer. J. Math., vol. 70 (1948), pp. 144-146.
F. BERI-IART, On the characterization of reductions of small order , J. Combinatorial Theory (B), to appear.
F. BERNHART AND S. GILL, An extension of Winn’s result on reducible minor neighborhoods , to appear.
G. D. BIRKHOFF, The reducibility of maps , Amer. J. Math., vol. 35 (1913), pp. 114--128.
C. CHOJNACKI, A contribution to the four color problem , Amer. J. Math., vol. 64 (1942), pp. 36--54.
K. DÜRRE, Untersuchungen an Mengen von Signierungen , Doctoral Dissertation, Technische Universität Hannover, 1969.
P. ERRERA, Une contribution au problème des quatre couleurs , Bull. Soc. Math. France, vol. 53 (1925), pp. 42-55.
PH. FRANKLIN, The four color problem , Amer. J. Math., vol. 44 (1922), pp. 225-236.
W. HAKEN, An existence theorem for planar maps , J. Combinatorial Theory, vol. 14 (1973), pp. 180-184.
H. HEESCH, Untersuchungen zum Vierfarbenproblem , B-I-Hochschulscripten 810/810a/810b, Bibliographisches Institut, Mannheim/Vienna/Zurich, 1969.
——, _Chromatic reduction of the triangulations T_e,e=e_5+e_7 _, J. Combinatorial Theory, vol. 13 (1972), pp. 46-53.
P. J. HEAWOOD, Map color theorem , Quart. J. Pure Appl. Math., vol. 24 (1890), pp. 332-338.
A. B. KEMPE, On the Geographical problem of the four colors , Amer. J. Math., vol. 2 (1879), pp. 193-200.
J. KocH, Computation of four color reducibility , Ph.D. Thesis, 1976, Department of Computer Science Report no. UIUCDCS-R-76-802, University of Illinois at Urbana-Champaign, Urbana, Illinois._
H. LEBESGUE, Quelques conséquences simples de la Formule d'Euler , J. de Math., vol. 9 (1940), pp. 27-43.
J. MAYER, Problème des quatre couleurs, un contre-exemple doit avoir au moins 96 sommets , J. Combinatorial Theory (B), to appear.
O. ORE AND J. STEMPLE, Numerical calculations on the four color problem , J. Combinatorial Theory, vol. 8 (1970), pp. 65-78.
T. OSGOOD, In existence theorem for planar triangulations with vertices of degree five, six, and eight , Ph.D. Thesis, 1974, University of Illinois at Urbana-Champaign, Urbana, Illinois.
R. STANIK, Zur Reduction von Trianggulationen , Doctoral Dissertation, Technische Universität Hannover, 1974.
W. STROMQUIST, Some aspects of the four color problem , Ph.D. Thesis, Harvard University, 1975.
W. TUTTE AND H. WHITNEY, Kempe chains and the four colour problem , Utilitas Mathematica, vol. 2 (1972), pp. 241-281, reprinted in Studies in Graph Theory, Studies in Math., Math. Assoc. of America, vol. 12, 1976.
P. WERNICKE, Über den kartographischen Vierfarbensatz , Math. Ann., vol. 58 (1904), pp. 413-426.
C. WINN, On the minimum number of polygons in an irreducible map , Amer. J. Math., vol. 62 (1940), pp. 406-416.
Added in proof. 在 1977 年 9 月 21 日,我们收到了以下预印本,其中包含本期刊第 491 页上提到的 2669 个 reductions。
K. DÜRRE, H. HEESCH, AND F. MIEHE, Eine Figurenliste zur Chromatischen Reduktion , Preprint No. 73 (1977), Institut für Mathematik der TU Hannover.
在这个列表中,我们发现我们的集合 \mathscr U' 的 415 个成员中 256 个是 D-可约的。我们还发现了 \mathscr U' 的 227 个成员的可约子构型(后者允许 \mathscr U' 的大小减少 77 ,因此当前最小的不可避免集合有 1405 个成员)。
对于所有出现在两个列表中的构型,该构型是否是 D-可约的看法相同。对于那些非 D-可约的构型,在应用 D-算法后,坏着色的数量是完全一致的(这些数字在微缩胶片补充中给出),除了 [30] 中的列表显示较少坏着色的两个 articulated 长 11 环构型之外。在这两种情况下,我们的结果与 Allaire 程序的结果一致。
第二部分:可约性
1. 介绍
在本文的第一部分中,一个放电过程被定义,该过程产生了环尺寸为 14 或更小的一组构型 \mathscr U 的不可避免性(在平面三角剖分中)。在这一部分中,\mathscr U 被展示(表 \mathscr U 由图 1-63 组成),并讨论了其成员的可约性证明。
当术语“可约性”在上面使用时,它以如下形式化的意义使用。\mathscr U 中的每个构型都具有这样的性质:它不仅在 [16], [27] 的定义中是 C-可约 或 D-可约的(参考文献是第 Part I 的参考文献),而且如果它被任意地浸入平面图中(即,不一定“正确嵌入”),则该平面图不可能是最小五色图。本文对这种“浸入可约性”进行了相当详细的研究。
除了一个例外,我们的计算机程序已经检查了 \mathscr U 中构型环尺寸为 11 或更大的每一种构型。对于较小环尺寸的配置的可约性,我们依赖于 [2] 中的表。我们并不是第一个证明所有这些构型可约的人。特别地,我们认为 F. Allaire 已经列出了一个完整的可约的 11 环的列表,而 H. Heesch 有一个尚未发表的可约构型的大列表。此外,由于我们没有应用 splicing arguments,因此存在 C-可约的构型我们无法找到可约证明 / reducer,其中一些出现在 [25] 和 [1] 中。但是,由于这只意味着我们的集合 \mathscr U 的一个小扩大,我们更喜欢在 \mathscr U 中只包括我们可以用程序验证的构型(见第 490 页底部的注释)。
我们要感谢 Illinois 大学研究委员会对计算工作的支持。我们得到了 Illinois 大学计算机服务办公室(C.S.O.)的大力帮助,不仅使用了 Urbana 的 IBM 360-75 计算机,还使用了 Chicago Circle 的 IBM 370-158 计算机和大学行政数据处理单元的 370-168 计算机。我们要特别感谢 C.S.O. 的顾问和系统程序员提供的出色帮助和建议,以及运营人员的出色合作。我们还要感谢 Laurel, Peter, Andrew Appel 仔细检查图表,并验证放电过程结果中构型的存在。
特别的,我们要感谢 Michael Rolle, Charles Mills, William Mills 指出了本文早期预印本中的复制错误。
PS:这上面最先进的 IBM 370-168 长这样:
我们的原则,即 reduce 所有要求的环尺寸大于 10 的构型,有一个主要的例外。在我们工作的早期,我们意识到我们无法 reduce(证明……可约)构型 16-14,如果可以 reduce 16-14,将使我们能够简化我们的论证过程。我们问 Frank Allaire 是否可以 reduce 16-14。他优雅的 splicing argument 为 C-可约性提供了一个 reducer。我们后来发现,这种构型从 \mathscr U 中消除了至少八种构型。虽然我们意识到 Allaire 的方法可以大大缩小 \mathscr U 的大小,但我们觉得向他询问我们感兴趣的所有其它构型是不合理的。然而,我们当然感谢他在这方面的帮助。
很明显,从最小构型的最短列表的意义上讲,我们的集合 \mathscr U 几乎肯定不是最好的可能生成猜想的一个证明的集合(见 Part I Section 5)。可以通过使用 splicing 技术来查找我们无法通过程序 reduce 的某些构型的 reducer,或者通过允许一些长 15 的环构型来避免更多的较小构型,或者通过在放电讨论中采取更多步骤来避免某些构型,或者通过选择放电过程产生的一些构型的不同子构型来缩短列表。我们不选择这样做,因为看起来缩短列表既没有显著改变证明的复杂性,也没有自然的位置停止尝试这种“简化”。然而,在对本文 Part I 进行缩微胶片补充时,我们发现 \mathscr U' 中可以省略 352 种构型,满足剩余的 1482 种构型仍然是不可避免的。\mathscr U-\mathscr U' 中的 352 种构型在缩微胶片补充资料中列出(见封底)。可约性计算与 Part I 所述过程的最终开发同时进行,使我们能够在必要时修改程序,以避免 reduction failures(这里,reduction failure 指的是我们的程序在分配的计算机时间内没有 reduce 的构型。我们知道,我们称之为 reduction failure 的大量配置实际上是 C-可约的)。
2. 计算机程序
D-reduction 是动态进行的(见 [2]),因为一旦一种着色被证明是好的,它的 goodness 就可以立即用于其他着色的测试。D-reduction 程序是 [20] 中程序的扩展和修改。
虽然 D-reduction 的任务相当直截了当,但 C-reduction 提供了某些选择。在处理好尺寸 / good-sized 的构型时,几乎不可能尝试所有可能的 reducer。一般来说,尽有限的努力寻找 C-reducers,并在必要时接受一定数量的构型作为 reduction failures,这似乎是合理的,这些构型只要付出更多的努力,就可以证明是可约的。虽然现在想起来,我们的选择可能不是最好的,特别是根据 splicing 理论,它们确实很容易地 C-reduce 了大量的构型。
对于每种环大小,从 11 到 14 ,我们尝试了一个“最佳猜测 / best guess” reducer,然后耗尽了某一类潜在的 reducer。如果以这种方式没有发现 reducer,或者在长 14 环的情况下,超过了我们的时间限制(在 IBM 370-158 上为 90 分钟,在 370-168 上为 30 分钟),则该构型被称为一个 reduction failure。这个过程有一类例外。对于长 11 环,为 [20] 开发的程序使我们能够测试最多四个内部顶点 / interior vertices 的所有 reducer。
我们会说明在长 12 环的情况下的 reducer 选择算法。首首先, best guess reducer 按如下方式选择。对于每一对环位置,(由 D-reduction 得到的)好着色数量被列成表格。reducer 通过选择尽可能多的 high-ranking compatible identifications、以这样 agreements 的数量中 pairs 的 rank 的顺序选择 identifications(丢弃与先前选择的 identifications 冲突的 identifications)形成。
第二类潜在 reducer 按如下方式选择。首先,所有不冲突的三元组 identifications,其中每个成员对应环上距离为 2 的顶点被尝试。如果这些尝试都没有 reduce 这个构型,则对具有最少坏着色的二十个进行进一步处理。首先,注意三个这样的 identifications 将 12 环转换为 6 环。因此,我们可以考虑这个 6 环的 reducer 和三个 identifications,以形成 12 环的一个 reducer。这是对二十个最好的三元组进行的,使用每个没有内部顶点的 6 环 reducer(见 [16]),每个 6 环 reduce 在每个可能的位置。对 11,13,14 环进行了类似的处理。
计算机程序在很大程度上受到可用设备的影响。我们可以使用 IBM 的计算机(Urbana-Champaign 的 360-75 计算机,芝加哥大学 Circle 校区的 370-158 计算机,后来是 Illinois 大学行政数据处理单元的 370-168 计算机)。出于这个原因,程序是用 IBM 汇编语言编写的,试图最大限度地提高效率。当我们询问时,操作人员建议我们以牺牲大量核心存储为代价,减少我们使用计算机的时间。因此,为了节省步骤,我们选择使用大表。核心存储要求如下:对于 12 环,220,000 字节;对于 13 环,600,000 字节;对于 14 环,1,700,000 字节。
使用四个通过的 D-可约构型对 reduction 时间进行采样,结果大致如下。在 360-75 上 11 环大约需要 40 秒;在 370-158 上 12 环大约需要一分钟;在 360-75(slow core)上 13 环大约需要 15 分钟,在 370-158 上则是大约 5 分钟;在 370-158 上 14 环大约需要 25 分钟,在 370-168 上则是 6 分钟。一般来说,如果 C-reduction 能够成功,它会很快结束,所以大部分时间通常用于 D-reduction。然而,reduction failures 通常需要大量的 D-reduction 过程和额外的 C-reduction 时间,因此通常需要上述 D-reduction 的四到八倍的时间。
3. 浸入可约性
平面三角剖分中 \mathscr U 的不可避免性,如 Part I 中所述,意味着每个平面三角剖分 \Delta (没有顶点的度数小于 5 )包含 \mathscr U 的至少一个成员,比如说 C ,作为浸入 f:C\to A 的像,且满足 degree-specifications(定义见 Part I Section 2)。证明每个 \mathscr U 中的构型 C 是 C-可约的或 D-可约的是不充分 / sufficient 的,因为 C 可能以使是 C-可约性与 D-可约性基础的某些独立性假设不成立的方式浸入一个平面三角剖分 \Delta 中。因此,我们必须详细讨论这种浸入可约性。
构型有时被认为是一个 n 环加上它的内部,但我们将使用以下术语。我们使用术语 构型 / configuration (如我们在 Part I 中做的)代表环内部的顶点、连接这些顶点的边和由这些边的 3 回路界定的三角形。对于构型 C 的每个顶点 V ,它的度数 \deg(V) 的一个 specification 被给出;特别是,从现在起我们假设 in every instant \deg(V) 被指定为数字 5,\cdots,11 中的一个(\mathscr U 中的所有构型都具有此属性;在图形中,我们根据 Part I 图的左列进行编码来指定 degree-specifications)。现在,每个构型 C 都可以扩展到一个 环化构型 / ringed configuration \bar C ,见图 A,使得 \bar C 是一个(平面中)圆盘的三角剖分,其中 C 的每个顶点都是内顶点,每个三角形都 is incident to C 的至少一个顶点;特别地,C 的每个顶点 V 精确地 is incident to 与为 \deg(V) 指定的 \bar C 的边一样多的边。注意,\bar C 是由 C 唯一(up to isomorphism)决定。我们称 \bar C 的边界回路 R 为 \bar C 和 C 的 环 / ring ,并且我们用 n 表示 R 中的顶点数(\bar C 的每个顶点要么是环顶点,要么是 C 的顶点)。C 和 R 之间的边(图 A 中的虚线)称为 \bar C 的 legs 。一个环化构型 \bar C 被称为 正确嵌入 / properly imbedded 到一个三角剖分 \Delta 中,如果每一对顶点的像在 \Delta 中相邻当且仅当它们在 \bar C 中相邻。
C-可约性和 D-可约性的定义保证了满足它们的构型不能将它们的环化构型正确嵌入到最小五色平面三角图中。然而,我们的证明涉及浸入而不是嵌入,我们必须确定 \mathscr U 的任何成员都不能浸入最小的五色平面三角剖分中。
为了形成我们关于浸入可约性的定理,我们需要几个定义。设 C 是一个构型(具有完全规定的顶点度数),\bar C 是相应的环构型,R 是环。设 V 是 R 的一个顶点,它在 C 中恰好有 k 个相邻顶点,并且 k\ge3 。这意味着恰好 k-2 个 V 的相邻顶点位于“C 的 1-legger outer sectors”上并且 V 在 \bar C 中有恰好 k+2 个相邻顶点。例如,在图 A 中,构型 C 是来自我们的集合 \mathscr U 的 21-34;“legs”被画成虚线,对于顶点 V ,我们有 k=5 (\mathscr U 中并未出现大于 5 的 k 值)。现在,我们可以通过将顶点 V “添加”到 C 并给它 degree-specification d(d>5) 来从 C 导出构型 C' 。C' 的环大小 n' 比 C 的环大小 n 小当且仅当 d\le k+2 。在这种情况下,我们称 C' 为 C 的一个 n -decreased 扩张;为了使这个概念可传递,我们称 C' 的任何 n -decreased 扩张也是 C 的 n -decreased 扩张。显然 C 的 n -decreased 扩张的数量是有限的。在我们的示例图 A 中,三个 C 的 n -decreased 扩张 C_{(1)}',C_{(2)}',C_{(3)}' 分别通过以 d=7,6,5 加入 V 得到。在 [26] 中 Stromquist 考虑了 d\ge k+2 的扩张 并将它们称为 r 扩张,其中 r=d-(k+2) ;即,图 A 中的 C_{(1)}' 是 C 的一个 0 扩张。泛化这个术语,我们应当称 C_{(2)}' 为 -1 扩张,C_{(3)}' 为 -2 扩张。
图 A
现在设 f:C\to\Delta 是一个单形浸入。显然,f 可以拓展为一个环化构形 \bar C 的 simplical 且 dimension-preserving 的映射 \bar f:\bar C\to\Delta (对于定义,见 Part I Section 2)。但是,\bar f 并非一定是一个浸入,因为对于某些环顶点的邻域,它可能不是 locally one-to-one 的。例如,在环顶点 V 映射到 \Delta 中的 5 度或 6 度顶点的情况中,图 A 中 \bar C 的像 \bar f(\bar C) 可能是(同构于)环化构形 \bar C_{(2)}',\bar C_{(3)}' 其中的一个;那么在像中,\bar C 的边 VA,VB 可能对应于(be identified to)对方或从 V 到 C 的 legs。我们称浸入 f 引起一个 内部重叠 / interior overlap ,如果 \bar f 在 \bar C 内部的限制(restriction of \bar f to the interior of \bar C )不是 one-to-one 的,即,如果 \bar f 将 \bar C 的两个不同三角形映射到 \Delta 的两个相同三角形。设 C 是 C-可约的,S 是一个 reducer。那么 f 被称为 与 S 兼容 / compatible with S ,如果任何两个被 S identified(be identified by S )的 R 的顶点都被映射到 \Delta 的不相邻的顶点,且任何两个被 S 的一个对角线连接的 R 的顶点都被映射到 \Delta 的不相邻的顶点。那么我们有如下引理。
引理 I:设 f:C\to\Delta 是不引起内部重叠的构形 C 到平面三角剖分 \Delta 的单形浸入。设 C 是 D-可约的,或者 C 是 C-可约的且有一个与 f 兼容的 reducer S 。那么 \Delta 不可能是最小五色图。
证明:设 R 是 C 的环,\bar C 是 C 的环化构形,\bar f:\bar C\to\Delta 是 f 在 \bar C 上的扩展。我们进行下列观察。
如果 \phi' 的原像 \phi 扩展到 \bar C 的一个着色 \psi ,那么 \bar f 将 \psi 带入到一个着色 \psi' (\bar f carries \psi into a coloration \psi' )且将 \phi' 在 \bar f(\bar C) 上扩展。
设 \phi 是 \bar f(R) 的一个着色,扩展到 \Delta-f(C) 上。如果 \pi 是一个将四种颜色划分成两对的划分,K' 是 \Delta-f(C) 中对应的 Kempe chain disposition,那么存在一个 \bar C 的外部 / exterior 的(abstract)Kempe chain disposition K ,与 \pi 和 \phi' 的原像 \phi 对应,使得 K 是 K' 如下意义的原像。(3a) 如果 V' 是 \bar f(R) 的一个顶点,那么 V' 的所有原像都被 K 的 Kempe chain 连接;(3b) 如果 \bar f(R) 的两个顶点被一个 K' 的 Kempe chain 连接,那么它们的原像被 K 的一条链连接。
如果 R 的一个着色 \tilde\phi (如 3 中考虑的)通过一个根据 \pi,K 的 Kempe interchange 从 \phi 中生成,那么 \tilde\phi 被 \bar f 带入到一个 \bar f(R) 的着色 \tilde\phi' ,且其可以通过(根据 \pi,K )的 Kempe interchange 从 \phi' 在 \Delta-f(C) 中生成。
如果 \bar f(R) 的着色 \phi' 在它无法通过 \Delta-f(C) 上的迭代 Kempe interchange 转换为在 f(C) 上扩展的任何着色的意义下是坏的,那么,通过 1 2 3 4,\phi' 的原像 \phi 也是一个坏着色,并且特别的,C 不是 D-可约的。
这说明了 C 是 D-可约的情况的引理。如果 C 不是 D-可约的,那么,通过假设,reducer S 与 R 的所有坏着色不兼容,并且因此 S 在 f 下的像,运用 5,与 f(R) 的所有坏着色不兼容。这说明了 C 不是 D-可约的情况的引理。\quad\blacksquare
推论:如果 C 是 D-可约的,如果 C' 是 C 的 0-扩张或 (-1)-扩张,那么 C' 也是 D-可约的。
证明:我们考虑环化构型 \bar C,\bar C' 与“自然的”浸入 f:\bar C\to\bar C' 与 f 的扩张 \bar f:\bar C\to\bar C' 。那么 f 不引起内部重叠,且我们得出与上面引理的证明一样的结论(在上面引理的 3 中,其中 K' 意味着在 \bar f(C) 外部的一个 abstract Kempe chain disposition)。注意,对于 0-扩张,推论可以从 Stromquist 的更强的定理得到([26] 中的 2-扩张定理和梯度定理 / gradient theorem)。\quad\blacksquare
注:可以想象(虽然不太可能)存在一个构型 C 与 C 的 0-扩张或 (-1)-扩张 C' 满足 C 是 C-可约的,但 C' 不是。C' “包含” C 这一事实不能用于证明 C' 的可约性,因为 \bar C 没有正确地嵌入到 \bar C' 中。这可能是因为 C 的所有可能的 reducer 都与浸入 f:C\to\bar C' 不兼容。现在我们考虑环化构型中的一个简单边路径 P ,它连接环 R 的两个不同的顶点 A 和 B ;(示例见图 B
图 B
和 图 C)。我们称 P 满足弯曲条件(fulfills a bend condition),如果存在一个 \bar C 中的顶点 V 满足 V 不在 P 上但与 P 上连续的(至少)三个顶点相邻(图 B 中标记的路径满足弯曲条件,但图 C 中标记的路径不满足)。\bar C 中的路径 P 被称作 I-路径,如果 P 连接两个 R 的顶点 A,B 并且满足如下性质:
如果 P 的长度为 5 ,那么 P 满足弯曲条件。
除了 A,B 之外,P 不包含 R 的任何顶点。
1. $P$ 的长度(即,$P$ 的边数)之多为 $6$。
2. 如果 $P$ 的长度为 $6$,那么 $P$ 满足弯曲条件。
3. $A,B$ 在 $R$ 上的距离至少为 $5$。
4. 除了 $A,B$ 之外,$P$ 不包含 $R$ 的任何顶点。
现在假设 $C$ 是 C-可约的,$S$ 是 $C$ 的 reducer。如果 $S$ 满足以下性质,则称其 fine。
(F.1) 如果环 $R$ 的两个顶点 $A,B$ 被 $S$ 识别,且 $R$ 上 $A,B$ 的距离至少为 $4$,那么存在一条 $\bar C$ 中从 $A$ 至 $B$ 的 I-路径。
(F.2) 如果 $R$ 的两个顶点 $A,B$ 被 $S$ 的一条对角线连接,且 $R$ 上 $A,B$ 的距离至少为 $5$,那么存在一条 $\bar C$ 中从 $A$ 至 $B$ 的 D-路径。
那么我们有如下定理。
定理:设构型 $C$ 包含 $m$ 个顶点、环大小为 $n$,满足 $n\le14$ 且 $n+m\le28$,设 $C_{(1)}',C_{(2)}',\dots,C_{(p)}'$ 为 $C$ 的所有 $n$-decreased 扩张,假设每一个 $C_{(i)}'$ 都是 $C$-可约或者 $D$-可约的,且存在一个 find reducer。那么 $C$ 就不能浸入最小五色平面三角剖分中。
证明:设 $f:C\to\Delta$ 是一个从 $C$ 到平面三角剖分 $\Delta$ 的浸入,$\bar f:\bar C\to\Delta$ 是 $f$ 在带有环 $R$ 的环化构型 $\bar C$ 上的扩展。我们需要证明 $\Delta$ 不能是极小的五色图。
(1) 如果 $n\le5$,证明很简单,因为 Birkhoff [10],$R$ 的像 $\bar f(R)$ 包含一个可约环,或者 $\Delta$ 含有至多 $29$ 个顶点。
(2) 现在我们假设 $n>5$,并由归纳,假设定理对所有 $<n$ 的环大小已被证明。
(3) 如果 $\bar f$ 不是浸入,那么 $f$ 在 $R$ 的某些顶点 $V$ 的邻域不是一对一的(比较图 A)。那么通过把 $V$ 加入 $C$,$\Delta$ 中包含 $C$ 的一个 $n$-decreased 扩张。那么由归纳假设 (2),$\Delta$ 不能是极小五色的。
(4) 现在我们假设 $\bar f$ 是浸入。那么特别的,$\bar f$ 不能区分任意两个在 $\bar C$ 中距离小于 $3$ 的顶点。
(5) 假设 $\bar f$ 区分了 $R$ 的两个顶点 $A,B$,且 $A,B$ 在 $R$ 上路径长度为 $3$ 或 $4$,那么 $R$ 上 $A$ 到 $B$ 的路径 $Q$(被 $\bar f$)满射到 $\Delta$ 上长度为 $3$ 或 $4$ 的环。如果在 $Q'$ 与 $f(C)$ 相反的一侧有 $\Delta$ 的任何顶点,则由 Birkhoff [10],$Q'$ 是一个可约环,因此 $\Delta$ 不能是极小五色的。如果在 $Q'$ 与 $f(C)$ 相反的一侧没有 $\Delta$ 的任何顶点,那么 $\Delta$ 包含 $C$ 的 $n$-decreased 扩张 $C'$(因为 $Q$ 上的 $A,B$ 间至少一个顶点可以作为一个 2-1egger 加入 $C$),我们再次得到 $\Delta$ 不能是极小五色图的结论。
(6) 现在我们假设 $\bar f$ 不区分 $R$ 中任意两个距离小于 $5$ 的顶点。
(7) 若 $\bar f$ 引起内部重叠,那么我们断言下述成立(对比图 D):
> 图 D
(7.1) $\bar f(\bar C)$ 是一个以 $\bar f(R)$ 中两个不相交的长度为 $5$ 的环 $P',Q'$ 为边界的圆环空腔(annulus)。
断言 (7.1) 的证明:$\bar C$ 是一个三角化圆盘(triangulated disk);设 $t$ 是 $C$ 中三角形的数量。(由欧拉公式可知 $t=2m+n-2$ 但是我们不会用到这个事实)如果 $D_i$ 是一个三角化圆盘,包含恰好 $i$ 个三角形,那么至少一个三角形 $T_i$ 满足如下两个条件之一(见图 E):
$T_i$(在 $D_i$)中属于 I 型,若 $T_i$ 的恰好 $1$ 条边 $E_i$ 是 $D_i$ 的内部边(interior edge),且 $T_i$ 其余的两条边 $G_i,H_i$ 是 $D_i$ 的边界边(boundary edge)。
$T_i$(在 $D_i$)中属于 II 型,若 $T_i$ 的恰好 $2$ 条边 $E_i,F_i$ 是 $D_i$ 的内部边,且 $T_i$ 的第三条边 $G_i$ 是 $D_i$ 的边界边,使得 $E_i,F_i$ 的公共点 $V_i$ 是 $D_i$ 的内部点(n interior vertex)。
如果 $T_i$ 是 I 型的,那么从 $D_i$ 中移除 $T-i-E_i$(即,移除 $T_i$ 的内部,$G_i,H_i$,以及 $G_i,H_i$ 的交点 $W_i$),生成一个三角化圆盘 $D_{i-1}$。如果 $T_i$ 是 II 型的,那么从 $D_i$ 中移除 $T_i$ 的内部与 $G_i$,生成一个三角化圆盘 $D_{i-1}$。根据 $T_i$ 在 $D_i$ 中是 I 型还是 II 型,我们分别称 $D_i$ 可以从 $D_{i-1}$ 通过 I 型或 II 型扩张生成。因此我们可以在 $t$ 步中通过三角化圆盘的序列 $D_1,D_2,\dots,D_t=\bar C$“构建”$\bar C$ 使得 $D_1$ 是一个三角形,$D_i$ 是 $D_{i-1}$ 的扩张(对 $i=1,2.\dots,t$)。
我们考虑浸入 $\bar f$ 下圆盘 $D_i$ 的像 $\bar f(D_1),\bar f(D_2),\dots,\bar f(D_t)=\bar f(\bar C)$。显然,$\bar f\mid D_1$ 是一个嵌入。设 $u$ 是最小的满足 $\bar f\mid D_u$ 不是嵌入的下标,那么我们遇到了图 F 所示的情况,即,$D_u$ 是 $D_{u-1}$ 的一个 I 型扩张,顶点 $W_u$ 的像 $W_u'
图 F
与 D_{u-1} 的一个边界点的像重合。(图 E,F,G,H 中画出的是曲线边界弧而不是任意长度的多边形弧线,\bar f 下的像用 \prime 标注,平行于 D_{i-1} 或 D_i 的细线表示 D_{i-1} 或 D_i 的内部如何被 \bar f 映射)特别的,\bar f(D_u) 的外部包含两个不相交的开区域,我们称之为 J_u,K_u 。(见图 F)J_u,K_u 的边界,我们分别将 J_u,K_u 的边界环称为 P_u',Q_u' ,在 D_u 的边界上类似地定义 P_u,Q_u ,其内部被一对一映射为 P_u',Q_u' (P_u,Q_u 的端点被映射到 W_u' )。
现在我们由归纳(见图 G )可得,对于每个 i=u,u+1,\dots,t ,D_i 的边界上存在两弧 P_i,Q_i (内部不相交)使得 P_i,Q_i 的内部被一对一映射到环 P_i',Q_i' 且 P_i 的端点被映射到 P_i' 的顶点 A_i ,Q_i 的端点被映射到 Q_i' 的顶点 B_i 。(在 \Delta 中 A_i,B_i 可能是不同的顶点,也可能是相同的顶点)特别的,P_i' 是一个开区域 J_i 的边界,Q_i' 是一个开区域 K_i 的边界,满足 J_i\subseteq J_{i-1}\subseteq\cdots\subseteq J_u 且 K_i\subseteq K_{i-1}\subseteq\cdots\subseteq K_u 。如果 T_i' 与 J_{i-1} (或 K_{i-1} )不相交,那么我们可以选择 J_i=J_{i-1},A_i=A_{i-1} (或 K_i=K_{i-1},B_i=B_{i-1} )。如果 T_i' 的内部在 J_i 中,那么我们遇到的图 G 所示的 (a) ... (h) 情况中的一种。如果 T_i 是 I 型的且 W_i' 在 J_{i-1} 中(情况 (a) (b))或者 T_i 是 II 型的(情况 (c) (d))那么我们可以选择 J_i=J_{i-1}-T_i',A_{i+1}=A_{i-1} 。如果 T_i 是 I 型的且 W_i' 在 J_{i-1} 的 P_{i-1}' 的边界中(情况 (e) ... (h)),那么 J_{i-1}-T_i' 的至少一个连通分量可以为 A_i 的选择作为 J_i,W_i' 。
现在我们考虑序列的最后一个元素,i=t (即,D_i=D_t=\bar C )并且我们忽略下标。那么,通过假设 (6),弧 P,Q 中的每一个在 R 中的长度都至少为 5 。除此之外,P 的端点与 Q 的端点不可能相同,否则,\bar f(\bar C) 会是一个到 D_u' 的同胚(见图 F),且 \bar f 不会引起内部重叠。因此,R-(P\cup Q) 非空,另一方面,R-(P\cup Q) 包含至多四条边(的内部)(因此根据假设,n\le14 )。因此,再一次使用假设 (6),P,Q 的端点的像 A,B 必须不同。现在,R-(P\cup Q) 包含少于四条边(的内部),否则,图 H 中所示的情况 (α) (β) (γ) 其中之一会出现。如果 R-(P\cup Q) 只包含两条边(情况 (α)),那么
图 H
这两条边映射到相同的边 E (因为 \Delta 不包含任何长度为 2 的环)且不可能出现内部重叠。如果 R-(P\cup Q) 包含恰好三条边(情况 (β) (γ)),那么这些边映射到三角形 T 的边界上,满足 T 的一条边 E 连接 A,B 。(因为 \Delta 除了三角形的边界外,不包含任何长度为 3 的环)但因此不可能存在内部重叠,否则,E (在 \bar f 下的)两个原像必须是 \bar C 中的对角线(一个环化构型不能包含任何对角线)。
因此仅剩的情况是 R-(P\cup Q) 包含恰好四条边,P,Q 均包含恰好五条边,且 n=14 ,这证明了我们的断言 (7.1)。
(7.2) 通过 (7.1),\Delta 不能是极小五色的,因为两个长度为 5 的环 P',Q' 中至少一个是可约的,或者 \Delta 至多有 30 个顶点。
(8) 从现在起,我们假设 f 不引起内部重叠。
(9) 如果 C 是 D-可约的,那么,从引理 I 可以直接得出,\Delta 不能是极小五色的。
(10) 从现在起,我们假设 C 不是 D-可约的,但是是 C-可约的,并且具有 find reducer S 。
(11) 如果 \bar f 将 R 的两个距离为 2 或 3 的顶点 A,B 映射到被 \Delta 中一条边 E' 连接的顶点 A',B' ,那么存在一条 R 上 A 到 B 的路径 Q 满足 \bar f(Q)\cup E' 是 \Delta 中一个长度为 3 或 4 的环 Q' 。那么我们可以得出(类似 (5) 中)Q' 在 \Delta 中的可约环或者 \Delta 包含一个 C 的 n -decreased 扩张 C' ,并且由归纳假设 (2),\Delta 不是极小五色的。
(12) 现在我们假设 \bar f 不将 R 上距离为 2 或 3 的点映射到 \Delta 中相邻的顶点上。
(13) 如果 f 与 S 不兼容,那么我们可以得出 \Delta 包含长度至多为 6 的环 Q' ,同时也是一条 I-路径在 \bar C 中的像加上 \Delta 中连接其端点的边,或者是一条具有可区分端点的 D-路径的像。在 Q' 的两侧,至少有三个 \Delta 的顶点属于 \bar f(R) 。现在我们分类讨论三种情况。
(13.1) 如果 Q' 的长度小于 6 ,那么由 Birkhoff [10],Q' 是可约的,因此 \Delta 不是极小五色的。
(13.2) 如果在 Q' 的某一侧有恰好三个 \Delta 中的顶点,那么这些顶点是 R 的三个连续顶点 U,V,W 的像。U,V,W 构成了一个 5-5-5 三角形(否则 Q' 的长度将大于 6 )。但这意味着 \Delta 的一条边连接 U,W ,这违反了 (12),所以这种情况被排除。
(13.3) 如果 Q' 的两侧都存在 \Delta 的至少四个顶点,如果 Q' 的长度为 6 ,那么 Q' 满足弯曲条件,由 Arthur Bernhart [6] 可知是可约的,因此 \Delta 不是极小五色的。
(14) 最后,我们假设 f 与 S 兼容。不过这时引理 I 蕴含着 \Delta 不能是极小五色的。这结束了该定理的证明。\quad\blacksquare
现在并不难验证我们的集合的所有构型够满足这个定理的假设。对于所有 0 - 和 (-1) -扩张的 D-可约性的 D-可约元素,直接从引理 I 的推论中得出,并且我们仅需单独检查极少数可能进行 (-2) -扩展的情况。对于不是 D-可约的构型,我们必须同样检查 0 - 与 (-1) -扩张。但大部分情况下,这些扩张包含,正确嵌入的,其余具有更小环大小的构型。我们也需要检查 reducer 是否是 fine 的。但是大部分构型非常小,所有 reducer 都是 fine 的(见补充文件)。
4. 可约构型的不可约集合 \mathscr U
此表格被组织成若干主要部分,由构型中每个度数的 major 顶点的数量决定。例如,图 1 中的构型没有 major 顶点,但图 16 中的构型有一对 $V_7$。除了此类相当小的情况外,例如具有两个 $9$ 度顶点的构型(见图 45),这类构型跨越了连续的完整图序列。在这些类中,排序更为随意,并不完全一致。外观相似的构型通常位于同一页上,例如,图 23 中的所有构型都有一个 $V_7$ 与一个 $V_8$ 相邻,下面有一个 $V_5$ 与两者相邻,上面有一个 $V_6$ 与两者相邻。有时,构型无法放入适当的图中,通常会在其自然位置的两页内,朝向图的底部。
试图获得合理的视觉显示导致一些图可能少于 $35$ 个条目。此外,当在表的最终检查中发现冗余时,冗余构型被删除,而不会向前移动剩余构型,引入潜在错误。缩微胶片补充 Section (β) 提供了有关表 $\mathscr U$ 的 C-可约(但不是D-可约)构型的更多信息。在补充材料中的每个图的上方是一对 $f-p$,它给出了所讨论的构型的图号和图中的位置。补充材料中的顺序与表中的顺序相同,除了在补充材料中绘制的图后添加了某些构型。在图中这以 heavy carat 表示。例如,5-32 和 6-13 之间的 carat 表示在表的末尾添加了一种构型,该构型应该放置于这个位置(构型为 5-35)。由于我们的 C-reducer 几乎所有都由对角线和标识(diagonals and identifications)组成,因此示意图如下绘制。首先,表 $\mathscr U$ 中的构型被复制一份。利用给出的构型的边界点的度数的信息,(不显示的)$n$-环可以容易地被读者画出。$n$-环上的顶点按顺时针顺序从 $1$ 到 $n$ 编号。此图的下面列出了所有标识和对角线。例如,构型 2-28 具有区分顶点 3 和 5,顶点 7、9 和 11 以及连接顶点 1 和 6、顶点 2 和 6、顶点 6 和 10 的对角线的标识。进一步,$m$(顶点数量)和 $n$(环大小)被提供。(在 2-28 的情况下,$m=8,n=12$)最后一个数字(对构型 $2-28$ 是 $6655$)给出了应用测试 D-可约性的算法后的坏着色数量。
以下数字为 $\mathscr U$ 提供了一些额外的线索。在 $1834$ 种构型中:
|环大小|数量|
| -----------: | -----------: |
|$\le8$|$7$|
|$9$|$8$|
|$10$|$35$|
|$11$|$89$|
|$12$|$334$|
|$13$|$701$|
|$14$|$660$|
$\mathscr U$ 中有 $504$ 种构型是 C-可约但不是 D-可约的。有关更多详细信息,请参阅缩微胶片补充 Section (ϵ)。
有 $13$ 种环大小小于 $11$ 的 C-可约构型未包含在补充材料中。这些构型在 [2] 的表格中被考虑。
> 图 1 - 图 63
当前进度:Part I 已完成,Part II 已完成,Part I 的 Introduction 与 BIBLIOGRAPHY 需要修订。