计数问题学习笔记

# 基础知识 ## 排列组合 ### 排列 从$n$个数字有序地选择$k$个数字的方案数。 第一个数字有$n$种选择方案，第二个有$n-1$ 于是答案为$n(n-1)(n-2)...(n-k+1)=\frac{n!}{(n-k)!}=n^{\underline{k}}$。($n^{\underline{k}}$指n的k次下降幂） 记为$P_n^k,A_n^k,{n\choose k}*k!$ 前两个好像是苏联的符号...? ### 组合 从$n$个数字个数字无序地选择$k$个数字的方案数。 因为无序，在排列的基础上除以$k!$即可 记为$C_n^k,{n\choose k}$ 同样地，国际上都喜欢用第二种。 ### 二项式定理 $(x+1)^n$中$x^k$前的系数。 等价于$n$个单项式中选$k$个取$x$，其余取$1$ 展开式： $$(x+y)^n=\sum_{k=0}^n{n \choose k}x^ky^{n-k}$$ ### 广义二项式定理 求$(x+y)^a$ （a是有理数） $$(x+y)^a=\sum^{\infty}_{k=0}\frac{a^{\underline{k}}}{k!}x^ky^{(a-k)}$$ 如果是正整数显然能那个分数能对应成刚刚的组合数 其他情况要泰勒展开，我不会。 ### 隔板法 n个一样的球放进m个不同的盒子，能不放，求方案数 把n个东西划分成m段，可以强行加m个球要求不能不放，那么就是在n+m-1个划分点选m-1个 答案为${n+m-1 \choose m-1}={n+m-1 \choose n}$ 以上是最简单的排列组合，下面的东西可能会让人懵掉。 ## 计数原理 ### 抽屉原理 把$kx+b(0<b<x)$个物品放进$x$个盒子内，至少有一个盒子内有$k+1$个东西 ### 加法原理 事件$A$有$n$个结局，事件$B$有m种结局，发生了一个事件，共有$(n+m)$种结局 若干不交的集合取一个的方案数，等于集合大小的和。 ### 乘法原理 事件$A$有$n$个结局，事件$B$有$m$个结局，两个事件都发生了，共有$nm$种结局 若干不交的集合格取一个的方案数，等于集合大小的乘积。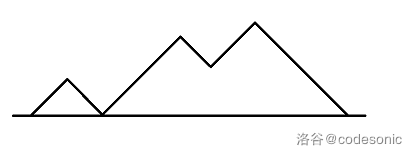 以上计数原理是计数的基石，虽然很浅显但是在后面的知识中扮演关键的角色、 ## 特殊数列 ### 卡特兰数 定义式： $$h_n=\sum^{n-1}_{k=0}h_kh_{n-1-k}(h_0=h_1=1)$$ 通项式： $$h_n={2n \choose n}-{2n \choose n-1}=\frac{{2n \choose n}}{n+1}$$ 应用场景很多 括号序列数量/$n\times n$方格行走数（不能越过对角线），凸多边形划分数，二叉树数量 用方格行走推导$h_n={2n \choose n}-{2n \choose n-1}$： 将模型转换成这样：  然后不能越过下面的直线 我们要走n次向上，n次向下，共2n次，这样我们才能回到0。 先忽略不能越过下面的直线，那就是在2n步中选出n步向上走，为${2n \choose n}$ 接下来减掉不合法的，如果越过了这个线，那么这时我们把终点(n,0)，改成(n,,-2)，进行一次**翻转**，就只需要走n+1步向下，n-1步向上，答案为${2n \choose n-1}$，这是一个**反射法**的经典应用。 ${2n \choose n}-{2n \choose n-1}=\frac{{2n \choose n}}{n+1}$可以用数学方法证明~~留与读者自证~~ ### 第一类斯特林数 用$S_u(n,m)$表示n个不同元素构成m个圆排列的方案数 1.最后一个元素单独做环 2.插入之前的m个环中 $$S_u(n,m)=S_u(n-1,m-1)+(n-1)*S_u(n-1,m)$$ 第一类斯特林数有时候有符号，在生成函数上应用较多，记为$S_s$ $$S_s(n,m)=(-1)^{n+m}S_u(n,m)$$ 有符号的斯特林数的生成函数为$x^{\underline{n}}$，这个结论非常重要，有了这个可以快速求斯特林数 建议明白生成函数后再回来看 ### 第二类斯特林数 $S(n,m)$表示把$n$个不同元素拆分进$m$个非空集合的方案数，集合不为空 $$S(n,m)=S(n-1,m-1)+m*S(n-1,m)$$ 类似于第一类斯特林数，考虑当前元素再新建一个集合和加入之前的集合即可。 $$S(n,m)=\frac{1}{m!}\sum(-1)^k{m \choose k}(m-k)$$ 这个式子可以用卷积快速计算，但是因为本篇主题是计数，所以不展开。 贝尔数（不要求划分成几个集合）是第二类斯特林数之和。 ### 拆分数 $f_n$表示大小为n的正整数拆分成若干无序的正整数和的方案数 有两种DP方法 1$.f_{i,j}$表示拆分成若干不超过j的方案数 $$f_{i,j}=f_{i-j,j}+f_{i,j-1}$$ 2.$g_{i,j}$表示拆分j个数字的方案数 $$g_{i,j}=g_{i-1,j-1}+g_{i-j,j}$$ 两个DP复杂度都是平方级别的。 考虑大小超过$\sqrt{n}$的数字最多只有$\sqrt{n}$个，结合两种DP，复杂度$O(n\sqrt{n})$ 用第一个DP考虑小的数字，用第二个DP考虑大的数字，先用f算出$\sqrt{n}$以内的答案，g的方程就可以改为$g_{i,j}=g_{i-\sqrt{n},j-1}+g_{i-j,j}$ 拆分数也有生成函数，为： $$\frac{1}{\Sigma(-1)^kx^{k(3k\pm 1)}}$$ 下面这个分母是带符号的五边形数 如果把拆分出来的正整数想象成柱形图，那么这两种方法一种是按列考虑，一种按行考虑。 # 生成函数 >生成函数的应用简单来说在于研究未知（通项）数列规律，用这种方法在给出递推式的情况下求出数列的通项 ## 多项式与形式幂级数 形式幂级数的定义： $$\sum _{n\geq 0}a_nx^n$$ 可以认为是一个有无穷次项的多项式，所有次项都为正 加减法： $$\sum _{n\geq 0}a_nx^n\pm \sum _{n\geq 0}b_nx^n=\sum _{n\geq 0} (a_n\pm b_n)x^n$$ 乘法： $$\sum _{n\geq 0}a_nx^n\times \sum _{n\geq 0}b_nx^n=\sum_{n\geq 0}(\sum _{k=0}^na_kb_{n-k}x^n)$$ 类似于多项式的加减法和乘法 ## 闭形式 形式幂级数的表达形式是一个长度无穷的多项式，但是对于部分的形式幂级数，存在长度有限的函数能够直接表示它，则称之为闭形 式。 比如等比数列： $$\sum _{n \geq0}x^n=\frac{1}{1-x}$$ $$\sum _{n \geq1}x^n=x\sum _{n \geq0}x^n=\frac{x}{1-x}$$ 意义：把无穷长度的形式幂级数改写为有限长度的闭形式 ## 组合对象 组合计数是一类常见问题，通常给定我们若干组合条件，对于每个组合对象，有某个函数 $size$ 衡量了它的大小，如图的节点数，序列的长度等。$size$ 为 $n$ 的个数为有限个，记为$A_n $，求某个$A_n.$ 这些图，序列等就是组合对象。 组合对象分为是否有标号的两种，指的是是否考虑组合对象内部的元素有不同的区别，例如无标号的三个点的图只有 4 种，而有标号的有 8 种。 ## 普通生成函数 数列$A_0,A_1,A_2...$的普通生成函数为 $$\sum _{n \geq 0}A_nx^n$$ 普通生成函数通常考虑无标号问题，它的加法操作和乘法操作分别对应了并和拼接两种操作。 ### 斐波那契数 $f_n$表示第n个斐波那契数，求$\sum_{n \geq 0}f_nx^n$的闭形式 令 $$F(x)=\sum_{n\geq0}f_nx^n$$ 由于$f_n=f_{n-1}+f_{n-2}$可得 $$F(x)=xF(x)+x^2F(x)+1$$ 解方程得 $$F(x)=\frac{1}{1-x-x^2}$$ 分解质因数后裂项，可得到通项公式。 ### 卡特兰数 求节点数为n的二叉树个数 生成函数本身具有组合性质，令$F(x)$表示该问题的生成函数，一棵二叉树可以划分成根节点和左右子树，是两个完整都二叉树， 所以$F(x)=xF^2(x)+1$，解方程可得$F(x)=\frac{1-\sqrt{1-4x}}{2x}$ 通过泰勒展开可以求得通项公式。 因为我不会 也不是主题内容，所以不展开 ## 指数生成函数 指数生成函数一般用来解决有标号问题 数列$A_0,A_1,A_2...$的指数生成函数为 $$\sum _{n \geq 0}\frac{A_n}{n!}x^n$$ ### 连通图计数 考虑到任意图可以被划分成若干连通图。 定义连通图的生成函数为$F(x)$，任意图的生成函数为$G(x)$。 很容易求出任意图的生成函数，即 $$G(X)=\sum _{n\geq 0}\frac{2^{n(n-1)/2}}{n!}x^n$$ 任意图是由连通图构成的，所以$G(x)=e^{F(x)}$，所以F(x)=ln G(x)，通过多项式姿势可以快速求出来 # Polya定理 ## Burnside 引理 ### 置换 置换就是对元素进行重新排列，必须（类似于线性代数中的**线性映射**）。 比如，把正方体旋转90度，可以看做四个顶点的一个置换 有以下结论： 置换可以构成环:从一个元素置换前到置换后连一条有向边，会构成环(循环） 定义一个状态S经过置换后与原来相同，则称其为不动点。 ### 置换群 置换群指的是一个置换的集合，满足任意两个置换不能复合出一个新的不在集合内的置换。 ### Burnside 引理 令$X$表示某个集合，$G$表示某个作用在X上的某个置换群。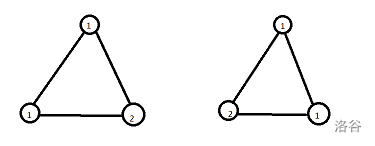对于任意$G$内的元素$g$，定义$f(g)$为$X$内经过置换$g$后不变的元素数量，我们要求$X$内本质不同的元素个数（本质不同指不能通过$G$获得彼此），这个个数记为$|X/G|$ （这也被称为**等价类**，求的也就是等价类个数） 形象地说，比如某个集合:  然后有一个置换为逆时针旋转60度，那这两个元素本质相同。 Burnside 引理为： $$|X/G|=\frac{1}{|G|}\sum_{g\in G}f(g)$$ 证明： > 我们发现一个元素是不是不动点需要考虑两个东西：一是元素本身，二是置换，所以不动点是**二元**的 例子： > 一个正方形分成4格,涂上黑白两种颜色,有多少种方案？其中经过转动相同图像的算一种方案 本来可以直接枚举，但是我们要验证Burnside ，所以对其加以考虑。 在这个正方形上的置换有： (1)顺时针转90度，(2)逆时针转90度，(3)不动，(4)直接转动180度 先把所有正方形画出来  然后按从上到下 从左到右一行一行编号为(1)~(16) 其中对于每个置换，列出不动点： (1):2个 (2):2个 (3):16个 (4):4个 $$|X/G|=\frac{1}{|G|}\sum_{g\in G}f(g)=\frac{1}{4}(2+2+16+4)=6$$ ### Polya定理 设$G$是$X$的一个置换群，$|X|$=n，用$m$种颜色染色，本质不同的方案数: $$L=\frac{1}{G}\sum_{g\in G}m^{c(g)}$$ $c(g)$表示$g$的循环节个数。 通常我们并不枚举所有的$g$，并计算$c(g)$，而是枚举 $c(g)$，快速计算多少$g$满足条件。 仍然将一个正方形分成4格,涂上黑白两种颜色,有多少种方案？其中经过转动相同图像的算一种方案 在这个正方形上的置换有： 不动：4 旋转90度 ：1 旋转180度 ：2 旋转270度：1 $M=\frac{1}{4}(2^4+2^1+2^2+2^1)=6$ # 生成树计数 ## 度数矩阵，邻接矩阵和基尔霍夫(Kirchhoff)矩阵 对于一个无向图$G$，定义$G$的度数矩阵$D$满足： $$d_{i,j}=\begin{cases} deg_i\space\space\space(i=j)\\0\space \space\space\space\space\space\space\space(i\ne j)\end{cases}$$ 其中，$deg_i$表示节点i的度数 定义$G$的邻接矩阵$C$满足： $$c_{i,j}=\begin{cases} 0\space\space\space\space\space\space\space\space\space\space(i=j)\\adj_{i,j}\space \space\space(i\ne j)\end{cases}$$ 定义$G$的基尔霍夫矩阵$L$：$L=D-G$，也就是： $$l_{i,j}=\begin{cases} deg_i\space\space\space\space\space\space\space\space(i=j)\\-adj_{i,j}\space \space\space(i\ne j)\end{cases}$$ ## 行列式 定义：一个矩阵$A$的行列式表示为: $$|A|=\sum _p(-1)^{\sigma(p)}\prod_{i=1}^na_{i,p_i}$$ 性质： 1.一个对角矩阵/上三角矩阵的行列式值是所有对角线上元素的乘积。 2.交换矩阵的两行/两列，行列式值取反 3.将矩阵的一行/一列乘上一个固定的常数 k，行列式值也乘上 k。 4.将矩阵的一行加到另外一行上去，行列式值不变，列同理。 可以使用高斯消元快速计算行列式。 ## 矩阵树(Matrix-Tree)定理 图$G$的生成树数量是依照以上步骤求出来的基尔霍夫矩阵$L$的行列式的任意一个代数余子式。 也就是说随意取它的任意一个$n-1$阶主子式，然后求出主子式的值，得到的就是在这个图中生成树的数量。 代码：咕咕咕 计数笔记就到这里结束了，以后可能会补一些例题什么的~ 接下来大概要学线代和数论/多项式~