树形DP
Echidna
·
·
个人记录
$update: 9.28$ **更新了[P3047 [USACO12FEB]Nearby Cows G](https://www.luogu.com.cn/problem/P3047)的思路和分析**
$update : 10.11$ **更新了[P4084 [USACO17DEC]Barn Painting G](https://www.luogu.com.cn/problem/P4084)的思路和分析**
----------------------
### 所谓树形DP,就是用来解决一些在树上的问题的DP。
### 树形DP可以分为很多类
- 树形DP+背包
典型例子:
**[P2014 [CTSC1997]选课](https://www.luogu.com.cn/problem/P2014)**
[P2015 二叉苹果树](https://www.luogu.com.cn/problem/P2015)
**[P1272 重建道路](https://www.luogu.com.cn/problem/P1272)**
[P1273 有线电视网](https://www.luogu.com.cn/problem/P1273)
- 选择节点的树形DP
基本特点是考虑的是每一个节点,不涉及背包
典型例子:
[P1122 最大子树和](https://www.luogu.com.cn/problem/P1122)
**[P1352 没有上司的舞会](https://www.luogu.com.cn/problem/P1352)**
**[P3047 [USACO12FEB]Nearby Cows G](https://www.luogu.com.cn/problem/P3047)**
**[P4084 [USACO17DEC]Barn Painting G](https://www.luogu.com.cn/problem/P4084)**
**加粗的题目**表示这篇博客中涉及到的题目。
~~我太弱了,没能做更多的树形DP~~
下面是针对每一题的思路。
------------
## P2014 [CTSC1997]选课
题目大概的意思是为了学分,你要修$m$门课。但是每一门课都需要之前学过铺垫的知识才能学。然后我们可以修$C$门课,求修完之后能获得的最多的学分。
首先,我们会发现这个题可以用暴力求解。暴力的方法就是直接dfs,枚举每一条和当前节点相连的边,然后进行下一次的dfs,但是时间复杂度却是不确定的 ~~(反正我推不出来)~~ 。所以我们要学习更加巧妙的算法 ~~(dfs也挺香的,但是万一爆了就不好了)~~
于是我们可以考虑DP。那么对于DP我们第一个想到的就是去推状态转移方程(记忆化搜索如果dfs写好了的话不需要)
对于树型DP,f的一般格式就是$f[i][j]$,其中$i$代表以$i$为根节点的子树,j不确定,根据每一个题目而定。那么对于这个题,我们可以设$f[i][j]$为以$i$为根节点的包括$i$的子树中,花费$j$的学习课程的机会能够获得的最多学分。这时回顾背包,发现这不就是背包问题吗?
状态转移方程为
$f[i][j]=max(f[i][j],f[k][t]+f[i][j-t]+s_k)
其中j为i的子节点,s_k为k的学分,t为分给j的子树的学习机会次数,并且明显1 \le t \le j 。
没看懂?没问题
为什么呢?我们为了求以i为根节点的子树、有j个学习机会的最大学分,必然会把这些学分分给每一个子树。所以就有了这个奇妙的转移方程。
现在我们回顾这个方程,发现为了求出f[i][j],我们需要先知道f[k][t]。很明显,t \le i,所以问题规模是在不断缩小的。为了求出f[k][t],我们又要去找k的子节点……
貌似还有一个问题:叶结点怎么办?叶结点只有两种状态:学或者不学。当学的时候,f[i][1]=s_i ;不学的时候,f[i][0]=0
这样的话,我们就能写一个用dfs实现的dp了 (有点怪)
这道题还有一个小技巧可以使用。因为数据是个森林(有多棵树),直接dp还得涉及数据的合并,非常难搞,我们可以假设每一门没有先修课的科目的先修课都是0,这样就把一个森林变成了一棵树。( 《 生 物 科 技 》 )
下面是代码:
#include<iostream>
#include<cstring>
using namespace std;
const int N=310;
int f[N][N]; //这个是DP数组
int h[N]; //i的学分
struct side{
int t,n;
};
side ss[N]; //链式前向星存图
int head[N];
int k=1;
void add(int f,int t){
ss[k].t=t;
ss[k].n=head[f];
head[f]=k++;
}
int n,m; //分别代表科目的数量,可以修的课的数量
void dp(int k){ //用dfs实现的dp
f[k][1]=h[k]; //不管怎么样,如果只选一门课,那只能选自己。
for(int nxt=head[k];nxt!=-1;nxt=ss[nxt].n){ //枚举每一个子节点
int to=ss[nxt].t;
dp(to); //因为要知道f[to][i],所以要先递归到to上,算出f[to]
for(int j=m;j>=1;j--) //枚举总的学习机会
for(int i=j-1;i>=1;i--) //枚举分给to的学习机会。
f[k][j]=max(f[k][j],f[k][j-i]+f[to][i]);
//因为这里实际上使用了滚动数组优化法,所以j一定要倒序枚举,否则在使用之前覆盖之前算出的得数。
}
}
int main(){
cin>>n>>m;
for(int i=0;i<=n+1;i++)
head[i]=-1;
for(int a,b,i=1;i<=n;i++){
cin>>a;
add(a,i);
cin>>h[i];
}
m++;
dp(0); //为了方便,我们假设0为所有没有父节点的根节点
cout<<f[0][m]<<endl;
return orz;
}
P1352 没有上司的舞会
这道题大概的意思就是如果一个人的上司参与了舞会的话,他就不会参与,否则反之。每一个人都有一个逗比 (弱智) 指数,请你编程计算如何安排可以让这个舞会的逗比指数最大。
首先按照上一个题说的技巧,我们可以快速地设f[i][j]为以第i个人为根的子树,
然后还是需要具体题目具体分析。
我们可以设f[i][j]为第i个人参加或者不参加的时候舞会上有的最大的逗比指数,j=0代表不参加,j=1代表参加。
如果这个人参加的话,那么他的下属都不会参加,所以我们需要把所有下属不参加的最大的逗比指数加起来,也就是\sum_{j \in son[i]}f[j][0] ;同时我们还要把这个人参加所增加的逗比指数加进去,总的状态转移方程就是这样的:
f[i][1]=v_i+\sum_{j \in son[i]}f[j][0],其中 v_i 代表i的逗比指数,son[i] 代表第i个人的下属的集合。
如果这个人不参加的话,那么他的下属有可能参加或者不参加,但他的逗比值不会加到舞会里。
所以总的状态转移方程是这样的:
f[i][0]=\sum_{j \in son[i]} max(f[j][0],f[j][1]) , 其中son[i] 代表第i个人的下属的集合。
对于这个题目,小的细节问题就是我们不清楚哪个人是老板(树的跟)。对此,我们可以在输入的时候统计每一个人的入度,如果这个人的入度为零,说明这个人是这个公司的老板,记为root。
分析到这里,其实题目的状态转移方程就已经出来了,剩下的就是套模板,用dfs的方式去完成dp。在每一个节点,计算这个人的f[i][0]、f[i][1]。最后dp完成之后输出max\{f[root][1],f[root][0]\} 即可。
代码:
#include<iostream>
using namespace std;
const int N=6e3+100;
int h[N];
int f[N][2];
int n;
struct node{
int t,n;
}nodes[N];
int head[N];
int k=1;
void add(int f,int t){
nodes[k].t=t;
nodes[k].n=head[f];
head[f]=k++;
}
int rd[N];
int root;
void dp(int k){
f[k][0]=0;
f[k][1]=h[k];
int nxt=head[k];
while(nxt!=0){
int y=nodes[nxt].t;
dp(y);
f[k][0]+=max(f[y][0],f[y][1]);
f[k][1]+=f[y][0];
nxt=nodes[nxt].n;
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++)
cin>>h[i];
for(int a,b,i=1;i<n;i++){
cin>>a>>b;
rd[a]++;
add(b,a);
}
for(int i=1;i<=n;i++)
if(rd[i]==0){
root=i;break;
}
dp(root);
cout<<max(f[root][0],f[root][1])<<endl;
return orz;
}
P1272 重建道路
这道题的基本意思就是:John的农场的道路被地震摧毁了,重建后形成了一个树状结构, John非常开心 ,并想让你计算如果再来一场地震,震出来一个有m个节点的联通块的最少的需要摧毁的道路是多少。
感觉这么说还是搞不懂啊,那就看看数据吧。
输入数据:input_1 输出数据:output_1
11 6 2
1 2
1 3
1 4
1 5
2 6
2 7
2 8
4 9
4 10
4 11
那么我们来看看这个题的数据:要求形成一个有六个点的独立联通块。现在看着这个图,然后我们就可以找规律了。如果我们找1,2,3,4,5,6这六个点的话,那么我们就要断开五条边(2\rightarrow7 , 2\rightarrow8 ,1\rightarrow3 , 1\rightarrow4 , 1\rightarrow5)才能让1,2,3,4,5,6变成一个独立联通块
如果我们选择 1,2,3,6,7,8 这6个点的话,我们只需要断开两条边就行了(1\rightarrow4 , 1\rightarrow5),这显然是正解(为什么呢?看看输出就知道了)。
如果实在还不了解题意的可以去看看这道题的题解 (太懒了)
我们仍然可以套树形DP的模板:设f[i][j]。i可以意思是以i为根节点的子树,但是j应该代表什么呢?我们看看这道题的未知数: 断开的路的数量 和 最多形成的最大独立联通块的大小 。咦?正好是两个量,那么一个是j 、一个是f[i][j]不就行了吗?还真是这样。
因为我们最终要求的是这棵树形成一个有m个节点的独立联通块的最小断掉的路的数量,所以如果设j为断掉的路的数量,不是很好写转移方程;如果设 f[i][j] 为断掉的路的数量,就会好写很多。 (这一段看得懂看不懂都无所谓。)
下面开始转移方程的推导。
对于一个有n个节点的子树,很明显最多可以断开n-1条边,不能再多了(没边可以拆了)。我们设 f[i][j] 为对于以i为根节点的子树,形成j的联通块所需要的最少的删边数量。我们需要分别考虑每一个子节点。
我们的思路就是父节点有j次删边的机会,我们就把这些机会分给j的子节点,然后看怎么分需要删的边最少,所以我们的转移方程就像这样:
这里的$-2$是为什么呢?我们的DP方程是$k$节点和父节点之间有边,所以要-1;
这颗子树和k节点之间还有一条边,所以要-1。相加就是-2了。
还有些大佬他们的做法是设$f[i][j]$为分给$i$节点$j$个删边的机会,并且$i$节点和父节点之间假设没边。他们这种做法就是$-1$了。但是$f$的初始化就和这里讲的不一样了。
这个转移方程各位大佬能看出来了,就是个背包。
很明显,我们可以看出来,$t \leq j$ 并且 $t \leq size_t-1$($size_t$代表以$t$为根节点的子树的节点数量),又因为这个DP方程其实是由三维压成了二维,所以**循环对于$m$应该倒序枚举。**
```c++
for(枚举每一个子节点)
for(int i=m;i>=1;i--)
for(int j=1;j<=min(i,nds[t]);j++)
//你的转移方程
```
把上述的一切拼在一起就是完整的程序了。
代码如下。
```cpp
#include<iostream>
#include<cstring>
#include<stdio.h>
#define int long long
//妈妈再也不用怕我忘了开long long了!
using namespace std;
const int N=600;
struct side{
int t,n;
}ss[N];
int head[N];
int k=1;
int du[N];
//f(i,j)代表从根节点为i的子树中截取j个节点所需的最少截断数(size(i)>j)
int f[N][N];
void add(int a,int b){ //链式前向星存图
ss[k].t=b;
ss[k].n=head[a];
head[a]=k++;
}
int nds[N]; //每一个节点(包括他自己)的子树的节点个数
int cl(int k,int fa){ //这个函数是用来统计将每一个点作为根节点的树的节点的个数的。
nds[k]=1;
int nxt=head[k];
for(;nxt!=0;nxt=ss[nxt].n){
int y=ss[nxt].t;
if(y==fa)
continue;
nds[k]+=cl(y,k);
}
return nds[k];
}
//对于每一个f(i,j),根据每一颗子树u,有
// f(i,j)=max(f(u,t)+f(i,j-t))
// 限制条件:t<=size(u) 且 u!=fa(i)
//对于这个方程,考虑循环嵌套顺序和方向。
//显然,应该j的枚举在外层,t的枚举在内层
//我们对于这个转移,需要之前的结果,所以如果j从小到大枚举的话,势必会破坏之前的结果。
//所以j应当从大到小枚举。
//t的顺序反而显得没有必要去一定从大到小或者从小到大,因此从小到大即可。
void dp(int k,int fa){
//尝试初始化显而易见的dp值
f[k][0]=1;
f[k][1]=du[k];
f[k][nds[k]]=1;
if(k!=1&&du[k]==1)
return;
//开始枚举每一条边,准备状态转移
int nxt=head[k];
for(;nxt!=0;nxt=ss[nxt].n){
int y=ss[nxt].t;
//检测这个点是否合法
if(fa==y)
continue;
dp(y,k);
for(int j=nds[k];j>=0;j--)
for(int t=1;t<j;t++)
f[k][j]=min(f[k][j],f[y][t]+f[k][j-t]-2);
}
}
int n,m;
signed main(){
cin>>n>>m;
if(n==m){
cout<<0<<endl;
return 0;
}
memset(head,0,sizeof(head));
memset(du,0,sizeof(du));
memset(nds,0,sizeof(nds));
memset(f,0x3f,sizeof(f));
for(int i=1;i<n;i++){
int a,b;
cin>>a>>b;
du[a]++;
du[b]++;
add(a,b);
add(b,a);
}
cl(1,-1);
dp(1,-1);
int ans=0x3f3f3f3f;
for(int i=1;i<=n;i++)
ans=min(ans,f[i][m]);
cout<<ans<<endl;
return orz;
}
```
如果还有什么不懂的话可以去看看这个题的题解,题解对于细节的讲解和处理比我说的详细的多。
## P3047 [USACO12FEB]Nearby Cows G
这道题目如果大佬一看,肯定会想到很多神奇的做法 ~~(蒟蒻都不会,然后自己想出了整个思路)~~
首先我们可以通过严谨的分析~~看标签~~发现这道题目的算法是树形DP。
既然是树形DP我们就应该还是拿出那一套。设$f[i][j]$为以$i$节点为根的子树中……
然后你会发现,这道题和之前的题有点不一样。这道题目没法再用背包,因为只要某个节点能被拓展到,它就可以被累加,而不是选择 ~~(有没有题目看错的?)~~,所以树形+背包那一套没用了。
取而代之的是什么呢? ~~(只有小孩子才做选择,我全都要)~~ 我们可以计算每一个子树**往下**看k层的所有节点的和。
然后有什么用呢?这又和题目有什么关系呢?题目给出的是这个节点往**四周**扩展k层啊,我们的程序没法直接应对这种询问。
但是,没法直接应对,不代表无法应对。如果你画一个图的话,你可以看出一些猫腻。首先我们先画出样例数据(以1为跟)
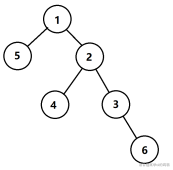
如果我们从第三个点开始拓展,我们可以先试着往下拓展。
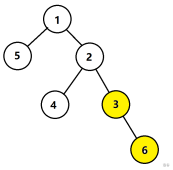
这样弄完了之后,我们再考虑上面的。如果我们直接把现在的值(也就是$f[3][2]$)加上$f[2][1]$的话,效果是这样的。
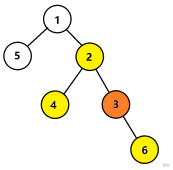
其中黄色代表加进去了一次,橙色代表加进去了两次。
我们会发现,节点$3$的值加进去了两次,这可不行,我们需要把它减去。怎么减呢?其实,$f[fa_i][j-1]$和$f[i][j]$的交集就是$f[i][j-2]$。你大可以画一棵完全二叉树看一下结果 ~~(这个蒟蒻找不到更好的证明方式了)~~
知道了这个,我们就可以说,节点$i$往上面扩展$1$层和节点$i$往下拓展$k$层的节点的和就是$f[i][k]+f[fa_i][k-1]+f[i][k-2]$。
我们已经成功往上推了一层,再推一层还不简单吗?
先把往上推一层的图像发一下。
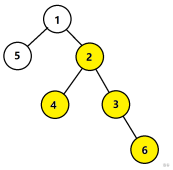
然后是往上面推两层的:
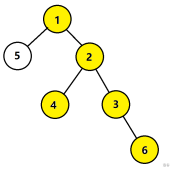
点$3$拓展$2$层的公式就是这个:
$spread(3,2)=f[3][2]+f[2][1]-f[3][1]+f[1][0]
这样点3就推完了。
根据这个方法,我们可以推出来任何一个点往上和往下推k层经过节点的和。
验证了思路的正确性,我们可以开始想DP了。(其实写题的时候是先写出来的DP,在想出来的往上推的方式)
我们容易得出:
为什么要max呢?**因为如果这个点往下的最多深度要大于j的话,它会把所有点全部取完,而不是是$0$。**
下面是程序了 ~~(更多的证明我咕了)~~
```cpp
#include<iostream>
#define int long long
#define FOR(k) for(int nxt=head[k];nxt!=0;nxt=ss[nxt].n)
#define TP ss[nxt].t
//define真香!
using namespace std;
const int N=2e5+10,K=22;
struct side{
int t,n;
}ss[2*N];
int head[N];
int k=1;//链式前向星存图
void add(int f,int t){
ss[k].t=t;
ss[k].n=head[f];
head[f]=k++;
}
int cs[N];//某个点的值
int n,m;
int f[N][K];//DP数组
int rd[N];//某个点的入度,用来快速判断这个点是不是叶结点。
int fa[N];//这个点的父节点(我们默认认为1是根节点)
void dp(int now,int fat){//DP
f[now][0]=cs[now];
for(int i=0;i<=m;i++)
f[now][i]=cs[now];
//这里for的作用懒得解释,如果不懂的话可以试着把这几行删掉,了解作用。
if(rd[now]==1&&now!=1){ //这里太坑了,如果点1只有一条边连着的话,
//程序会判断是叶结点,所以需要特判。
return;//如果是叶结点的话,直接返回,因为叶结点没什么好往下拓展的
}
FOR(now){
if(fat==TP)
continue;
dp(TP,now);
for(int j=1;j<=m;j++)
f[now][j]+=f[TP][j-1];
}
}
void dfs(int now,int father){
//这里的dfs是用来判断每一个点的父节点的。
//因为这个东西在dp()里算老是锅,就额外写了个dfs
fa[now]=father;
FOR(now){
if(TP==father)
continue;
dfs(TP,now);
}
}
//这个函数的作用是向上拓展,是用dfs实现的。
//你也可以使用bfs实现,但是我老是锅,没办法。。。
int spread(int a,int b,int ans){ //a代表现在的点
//b代表可以往上拓展的层数,ans代表答案。
if(a==1)
return ans;//对于a=1的特判。
if(b==1)//假如可以拓展的层数没有了的特判
return ans+f[fa[a]][b-1];
if(fa[a]==1)//如果到了根节点
return ans+f[fa[a]][b-1]-f[a][b-2];
ans+=f[fa[a]][b-1]-f[a][b-2];//一般情况
return spread(fa[a],b-1,ans);
}
signed main(){
cin>>n>>m;
for(int a,b,i=1;i<n;i++){
cin>>a>>b;
add(a,b);
add(b,a);
rd[a]++;
rd[b]++;
}
for(int i=1;i<=n;i++){
cin>>cs[i];
}
dfs(1,-1);
dp(1,-1);
for(int i=1;i<=n;i++){
cout<<spread(i,m,f[i][m])<<endl;
}
}
```
## P4084 [USACO17DEC]Barn Painting G
这道题目的大概意思是:这里有一棵树,有些节点的颜色已经告诉你了,你需要给其他的节点涂颜色,使得每一个节点的颜色都不与相邻节点的颜色重合,求方案数。
这道题我们选择可以从叶结点往根节点涂颜色,那么我们需要做的就是保证你要涂的节点的颜色和它的子节点的颜色不同。所以这道题的最大的问题就是有些节点的颜色已经固定了,你不能更改,只能让它影响你的方案数。
我们可以设$f[i][j]$为以$i$节点为根结点的子树中,节点$i$被涂成了颜色$j$的总方案数。因为这里我们设的是子树,所以我们不用在意这个节点的父节点有没有被涂色。如果这个节点的所有子节点都没有被固定颜色的话,状态转移方程为:
$f[i][j]=\prod_{p\in son[i]}\sum^3_{k=1,k\neq j}f[p][k]
其中 “ \prod ” 为连乘号,也就是把它后面连着的全部乘起来。
那么为什么是这个状态转移方程呢?假如这个节点有两个子节点,那么只要这两个子节点的颜色不和父节点重合,它们之间没有任何关系和影响。所以这里满足乘法原则:做一件事,完成它需要分成n个步骤,做第一 步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法。那么完成这件事共有 N=m1×m2×m3×…×mn 种不同的方法。
但是呢,对于每一个节点,它选择了一种颜色它就不能选择其他的颜色。这里就满足加法原则了:做一件事情,完成它有n类方式,第一类方式有M1种方法,第二类方式有M2种方法,……,第n类方式有Mn种方法,那么完成这件事情共有M1+M2+……+Mn种方法。
现在我们弄懂了如果子节点没有已经涂颜色的点的时候状态转移方程的推法。现在考虑其他的问题:如果这个点的子节点有已经被涂颜色了呢?很明显,这时我们不能把这个点的颜色涂成跟这个点的颜色是一样的。状态转移方程其实完全没有改变:我们设集合K为这个点可以选择的颜色,如果你要涂的颜色不在K中,那么我们就把这个颜色的f设为零。
说句人话就是:不让涂我就留0。
这个问题解决了之后,还有最后一个分问题:如果这个点是已经被涂了颜色的点,怎么办?
我们设这个点的颜色是c,那么如果这个点已经被涂了颜色的话,很明显,K=\{c\},也就是说,我们对于这个点只能选择涂c颜色。那么我们要不要直接粗暴的把这个状态转移方程的值赋为0或者1呢?
不能这样做。我可以画一个图,解释一下这种情况怎么做。
尽管红点的两个子节点的父节点是已经被染了色的点,我们仍然有四种染色的方案。如果我们直接把红点的dp的值写成1或者0的话,这会和正解不一样。
所以如果这个点已经被染色了,那么状态转移方程会是这样的:
f[i][c]=\prod_{p\in son[i]}\sum^3_{k=1,k\neq c}f[p][k]
所以这和上边的方程有区别吗?
有区别。区别就是除了c其他的颜色都是0。
如果您还是不能理解的话,您可以对照一下样例的图和dp数组的值自行理解。
dp数组的值:
4 4 0
1 1 1
1 1 1
0 0 1
树状数组实在是累死了,这篇博客到这里一应该结束了,后续可能不会更新了。
接下来我可能会去学线段树、数位DP、状压DP、斜率优化DP之类的数据结构和算法。
最后骗一波赞
这篇博客中有些题是我在做完好多天之后才写的,对于一些题的印象可能不是很深了,如果有错误和疏忽还请指出,感激不尽!