梦熊 2025 省选集训营 做题笔记
沉石鱼惊旋
·
·
算法·理论
20250204 模拟 T1
删点 MST,3\leq n,m\leq 5\times 10^5。
Sub 1
暴力模拟。或者写正解没上数据结构优化。
## Sub 2
数据随机。哈哈我也不会。
赛时没几个人会的档。由于随机所以造出来的树每个点度数都不多,暴力维护连通块。没写,大概就这个意思。
## Sub 3
一条链 $(i,i+1,1)$ 然后后面随便连点边。
MST 一定是这条链。
一次只会分成两个连通块。就是求 $u\lt i\lt v$ 的最小边权。
扫描线一下。
## 赛时提交记录
<https://mna.wang/contest/submission/765776>
## 正解
前言:删边 MST 版本。
<https://atcoder.jp/contests/JAG2013Spring/tasks/icpc2013spring_e>
<https://codeforces.com/problemset/problem/827/D>
<https://codeforces.com/problemset/problem/1184/E3>
我因为做过然后一时半会儿没转过弯来调了一个多小时倒闭了。GGG。
场上的时候我先是注意到了增量是 $\mathcal O(n)$ 的,一直在想处理每条边对应的可替代边,然后去重,掐头掐尾。
写了一下这个的暴力版本过不去拍但是过了大样例的第一个。我想先把这个改对了再套树剖,没测别的大样例。一直挂,寄寄寄。这个看起来可能有点对但是不太靠谱。
这个做法的主要思路和 std 都差不多。唯一问题好像是,我不能很方便的判断出子树之间的连边?
不管了,反正随便和我重写的 std 做法很像,代码复制黏贴一点改几句话就过了。糖糖的。
考虑类似删边 MST 的做法。删边 MST 要把贡献放到边上,我这里还是放到边上,删点就是删掉相邻边,然后就寄了。
把贡献放到点上,然后就全对了。子树可以连到一个祖先,或者连到其他子树。连到祖先的部分是链上 checkmin 然后单点求值。这个大力树剖,或者一个很简单的写法是对权值从小到大排序,覆盖一个点就删一个点,这里可以并查集维护删点,删点就是合并到父亲。
发现 $(u,v)$ 只可能是删掉 $\operatorname{lca}(u,v)$ 的时候才会用这条边合并两个子树。这样的话一条边只会在一个点贡献。均摊是对的。然后再做一个 $\mathcal O(deg)$ 个点的 MST。
代码非常好写!!1
但是不妨碍我模拟赛的时候和弱智一样!!1
<https://mna.wang/contest/submission/766572>
# 20250205 模拟 T1
有 $n$ 个点 $x_i$,每次从 $x_i$ 出发必须跳到 $[x_i+L,x_i+R]$ 之间的一个点 $x_j$。
每个点 $x_i$ 有元素 $a_i$。找到一个跳跃方式,使得经过的 $a_i$ 降序排序之后字典序最大。
无法到达输出 $-1$。
$1\leq n\leq 5\times 10^5$,$1\leq x_i,L,R\leq 10^9$,$1\leq a_i\leq n$,$x_i\lt x_{i+1}$。
## 特殊性质
$a_i$ 是排列。
zzk 说是因为不知道怎么放部分分放了个这个。他不知道怎么做。
我也不知道哈哈。
好像是说按位贪心可以做。但是想到这个就死翘翘了。和正解一点关系没有,大概是没法优化到正解复杂度的。
## Sub 1
$n\leq 500$。
发个考场时的笔记。
> 枚举点 $i$,枚举前驱点 $j$。
>
> 每个点维护一个序列表示目前的答案方式
>
> 点 $i$ 的最优序列是点 $j$ 在某个位置插入 $a_i$ 得到的
>
> 比较大小二分 lcp。序列只要维护一个前缀 hash 然后可以单点求值即可。
哈哈这个是正解。三方是实现这个暴力用 vector 然后暴力枚举 $j$ 比较。
代码不想交梦熊,这里贴一下主函数。
```cpp
int main()
{
read(n, L, R);
for (int i = 1; i <= n; i++)
read(p[i]);
for (int i = 1; i <= n; i++)
read(a[i]);
vec[1] = {a[1]};
for (int i = 2; i <= n; i++)
{
int l = lower_bound(p + 1, p + n + 1, p[i] - R) - p;
int r = upper_bound(p + 1, p + n + 1, p[i] - L) - p - 1;
for (int j = l; j <= r; j++)
{
if (vec[j].empty())
continue;
auto v = vec[j];
auto it = v.begin();
for (; it != v.end(); it++)
{
if (*it < a[i])
{
v.insert(it, a[i]);
break;
}
}
if (it == v.end())
v.insert(it, a[i]);
checkmax(vec[i], v);
}
}
write(vec[n].size(), '\n');
for (int i : vec[n])
write(i, ' ');
putchar('\n');
return 0;
}
```
缺失部分在梦熊交了 $\mathcal O(n^2\log n)$ 的。不影响理解。
但是这个是错的,我没判 -1。
## Sub 2
$n\leq 5000$。
$n\leq 500$ 的做法转移是一个提取区间 max。套个单调队列或者线段树就好。我写了个线段树,复杂度 $\mathcal O(n^2\log n)$。
<https://mna.wang/contest/submission/767064>
## 正解
首先这个转移形式是一段区间的 max 并且区间端点单调,所以可以单调队列维护。
开一个主席树,支持单点插入即可。
找 lcp 可以用 sum hash。看左子树的 hash 是不是一样,如果左子树一样就找右子树。为了避免冲突提前把每个 $[1,n]$ 映射到 $[0,p)$。
然后似乎没什么难写的,注意一下这题从大到小主席树值域要倒过来。
<https://mna.wang/contest/submission/776878>
# 20250205 模拟 T2
省流:Monster 的 DAG 版本。
给定 DAG,每个点有一个怪兽两条属性,花费 $a_i$ 血量击杀他然后回复 $b_i$ 滴血。求最小初始血量。
原题:<https://qoj.ac/contest/1221/problem/6406>。
$2\leq n+m\leq 72$,$1\leq a_i,b_i\leq 10^{15}$。
这个题有点乱,晚点好好补一下各档分的做法。
先写一下我的赛场做法。最高目前过了 96pts 的分。
数据很小,模拟退火,甚至还是阉割版,我不会完整的模拟退火。先随便拉一条 DFS 序下来,然后直接随机交换,更优就替换答案。然后次数开大点用 bitset 存一些目前可达的点集就差不多了。随便来一发就 84 了。随便调调参可以 96。
<https://mna.wang/contest/submission/767450>
然后为了获得 100 分,我们缝合一下 Cfz 的,数据分治一下。
> 显然有一个状压 DP。
>
> 但是状态数不满。
>
> 直接 map 存状态然后 BFS。
就过了。
Cfz 这个可以加点神秘的东西不是我这个做法给数据分治成 100。
**后续补。**
# 20250205 模拟 T3
求 $n$ 个盒子放 $m$ 个左括号,每个盒子都是合法括号序列,并且不存在一个盒子有 $k$ 个左括号的方案数。
$1\leq n,m\leq 10^7$,$1\leq k\leq m$,$10^8\leq p\leq 10^9+7$。
反射容斥和拉格朗日反演啥的都太难了,来点我学得会的做法。
首先显然套一个容斥,把不能有 $k$ 个左括号的限制消掉。然后 DP。$f_{i,j}$ 表示 $i$ 个盒子装 $j$ 个左括号的方案数。
这个有个显然的 $\mathcal O(n^3)$ 的,枚举这个盒子放多少左括号,转移显然。
这样就三方了。
## 特殊性质 1
$k=m$。
我也不知道是什么,会这个就会整个题了吧。
## 特殊性质 2
$p=998244353$。
一眼 NTT。但是有人说被卡常了,反正我不会 NTT 不关我事 >_<
## 正解
先随便说个东西。这个 $f_{i,j}$ 打表出来形如
```plain
1 0 0 0 0 0 0 0 0 0 0
1 1 2 5 14 42 132 429 1430 4862 16796
1 2 5 14 42 132 429 1430 4862 16796 58786
1 3 9 28 90 297 1001 3432 11934 41990 149226
1 4 14 48 165 572 2002 7072 25194 90440 326876
1 5 20 75 275 1001 3640 13260 48450 177650 653752
1 6 27 110 429 1638 6188 23256 87210 326876 1225785
1 7 35 154 637 2548 9996 38760 149226 572033 2187185
1 8 44 208 910 3808 15504 62016 245157 961400 3749460
1 9 54 273 1260 5508 23256 95931 389367 1562275 6216210
1 10 65 350 1700 7752 33915 144210 600875 2466750 10015005
```
然后观察一下,第 $1$ 行和第 $2$ 行只差一位,而第 $1$ 行是卡特兰数,说明第 $2$ 行是一个类似卡特兰数的转移,多个 $\pm 1$。然后撞几个式子就出来了。令人汗颜。
<https://mna.wang/contest/submission/768314>
这个正经做法我还不会,晚点写。
**后续补。**
# 20250206 模拟 T1
给定长度为 $n$ 的序列 $x_i$。定义 $f(x_i)=(a\oplus x_i)-b$,其中 $\oplus$ 是异或。
有 $q$ 次操作每次形如:
1. `1 k v` 表示 $x_k\gets v
2 a b 表示求出一个 i 满足 f(x_i)f(x_{i+1})\leq 0。无解输出 -1。
## 特殊性质
不带修。
<https://qoj.ac/problem/9669>
和正解一起讲,事实上会了这个就会正解了。
## 正解
我很不理解这个题出出来有什么意义,如果只是为了科普这个题很牛逼的这个做法完全可以开成强制在线。$10^6$ 卡掉了 $\log^2$ 也卡掉了正解的 $\log$。
不带修的版本求出最小的 $f(x)$ 和最大的 $f(y)$,那么如果有 $f(x)f(y)\leq 0$ 那么一定有解。
我们可以考虑如果此时还有一个 $z$ 那么 $f(x)f(z)$ 和 $f(y)f(z)$ 一定有一个 $\leq 0$。原因显然。
那么我们直接分治就对了。每次取 $mid=\frac{x+y}{2}$,然后递归跑下去。直到区间长度为 $2$。
带修的话在字典树的叶子结点加一个可删堆就好了,小心一些空间什么的。
糖题。线下评测还把我空间卡了。麻麻思乐。
<https://mna.wang/contest/submission/768709>
# 20250207 模拟 T1
每次操作选择当前位置抬高一格或者下个位置降低一格。操作永久保留。走到 $n$ 就回到 $1$。高度相同才可以通行。问走 $k$ 轮的最小操作次数。
## 正解
太简单了不写部分分做法了。
不难发现一个位置如果下降了就不会上升。而且下降的一定是后缀。所以需要先把后缀拍平。
然后 $k=1$ 答案就是极差,因为可以证明我们做降低操作是不优的。这说明我们每一轮答案都是极差。
然后继续观察一下每一轮相当于是删掉了最左侧的元素。那么直接前缀和维护一下就做完了。
<https://mna.wang/contest/submission/770764>
# 20250207 模拟 T2
构造不超过 $V$ 个点 $E$ 条边的有向图使得外向基环树大小是 $k$。
$V=80$,$E=220$,$1\leq k\leq 10^{18}$。
**可以有重边和自环。**
## Sub 1 & Sub 2
$V=130$,$E=400$,$1\leq k\leq 10$。
$V=130$,$E=400$,$1\leq k\leq 100$。
直接连 $k$ 条边就做完了。
## Sub 3
$V=130$,$E=400$,$k=2^t(0\leq t\leq 20)$。
构造 $t+1$ 个点的链,中间每个点连 $2$ 条边。
## 正解
这是 std 做法。
然后是 Cfz 做法。
妈的我赛时做了个完全一样的做法啊???然后我和【数据删除】赛时开黑,我俩认为我的做法应该对着加法构造加法器。但是这个很糖,做不了,因为一条边的贡献和两条边是不一样的。他并不是局部做了一个乘法最后可以加回来。然后发现这个东西啥都过不去。
但是这个做法的式子其实是加法乘法拼起来了,所以可以改。
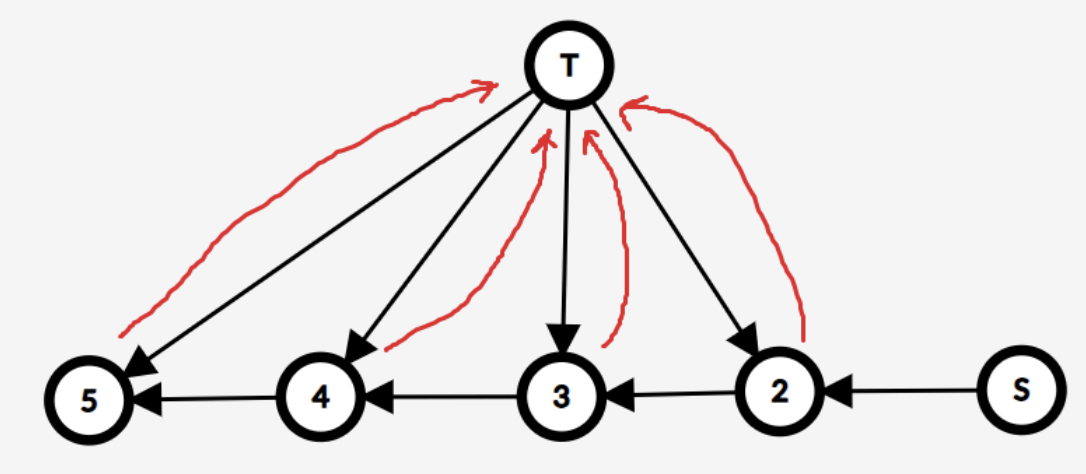
这个方案数是 $AB+AC+CD$。同理画更多点的图出来。
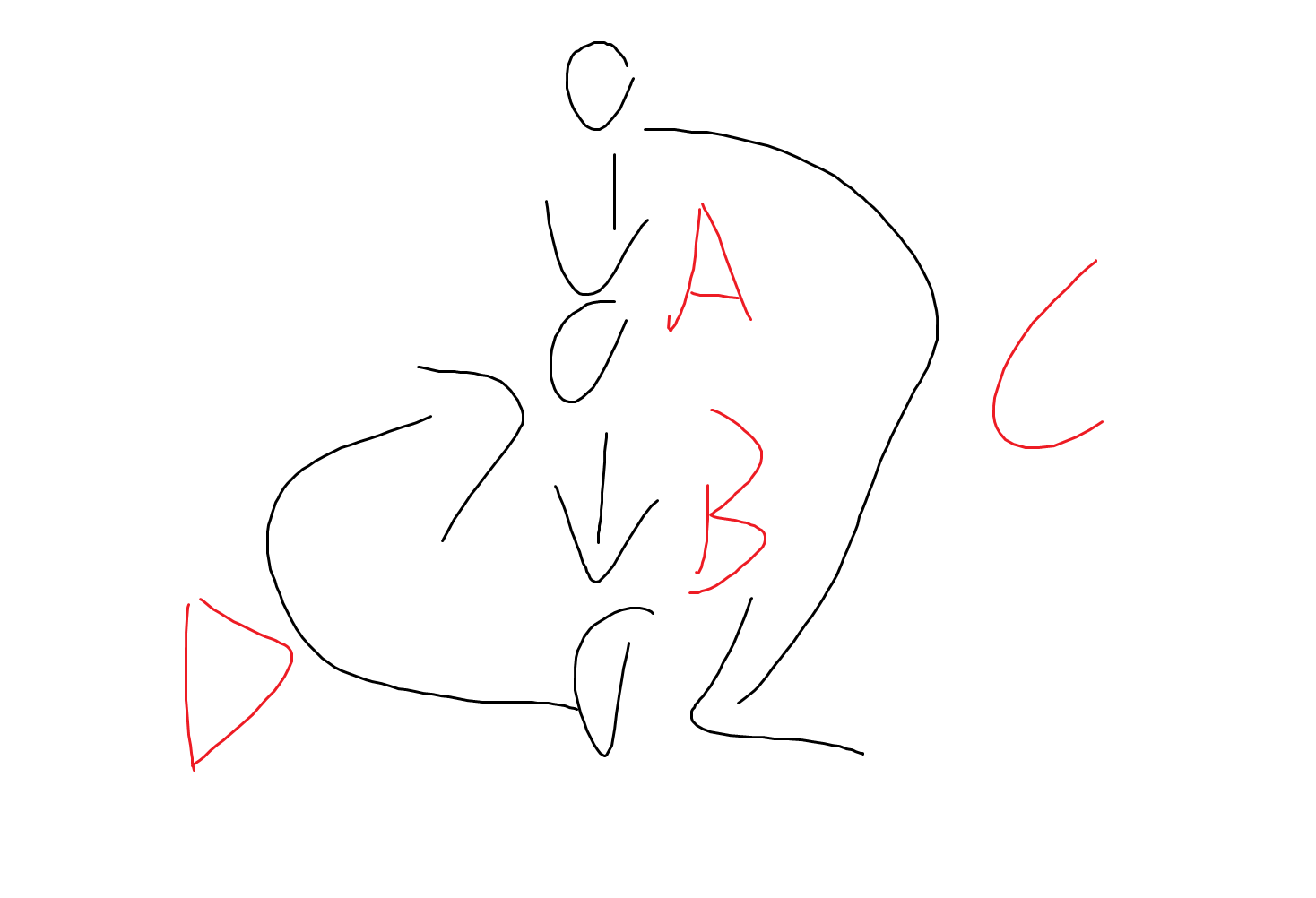
我们令 $A=B=E=F=1$,那么方案数是 $1+D(1+G)$。
同理边上连 $k_i$ 条生成树个数就是 $1+k_1(1+k_2(1+\dots))$。
然后这个直接就好了。。。奇数连一条偶数连两条是 $\log$ 但是常数倍。这个问题不大,奇数找一下 $\leq 7$ 的质因子除掉,就过了。
# 20250207 听课笔记
随机算法。
Monte Ciallo 算法