题解:P2296 [NOIP2014 提高组] 寻找道路
lusq
·
·
题解
P2296 [NOIP2014 提高组] 寻找道路
更新
## 思路
题意:找到有向图 $G$ 上连接 $s,t$ 两点最短的路径 $l$ 使得对于 $l$ 上的每个点 $u$,所有 $u$ 所指向的点都能到达点 $t$。
如果你没看懂这句话,你可以理解成:找到从一点到另外一点的最短路径,使得路径上就算走错一步,还是可以到达终点。
很明显,我们需要判断对于每个点能不能到达终点,再在所有指向的节点都能到达终点的节点中找最短路。
要判断哪些节点能到达终点,我们可以从终点反向搜索,所有搜索到的节点都能到达终点。
最后再用 BFS 求一遍最短路,保证路径上所有节点指向的节点都能到达终点即可。
为了方便读者理解,这里放一组样例来解释:
如图,假设节点 $1$ 为起点,节点 $4$ 为终点。
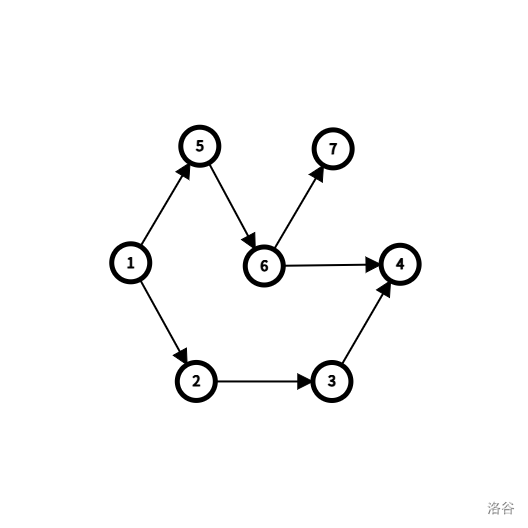
接下来我们从终点 $4$ 反向搜索,发现只有节点 $1,2,3,4,5,6$ 可以到达终点 $4$。
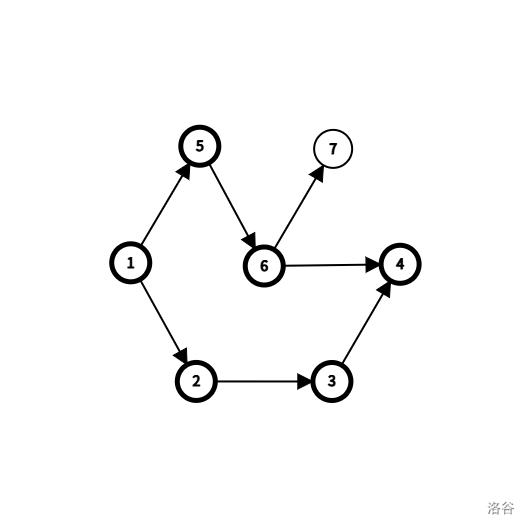
但是由于节点 $6$ 指向的节点 $7$ 不能到达终点 $4$,因此节点 $6$ 也不能作为最短路径上的点。
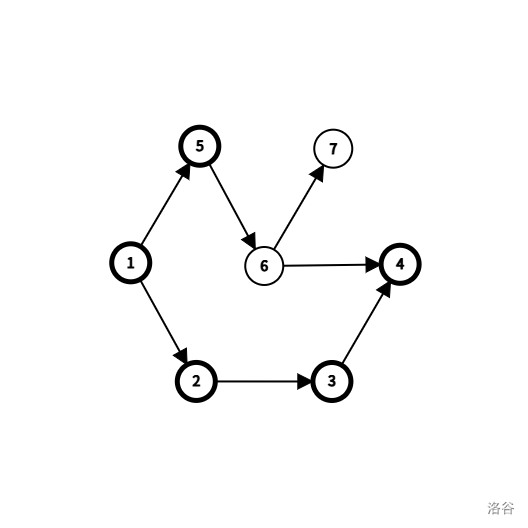
在剩下的节点中,从起点 $1$ 走到终点 $4$ 的最短路径为 $1 - 2 - 3 - 4$,长度为 $3$。
## code
```cpp
#include<bits/stdc++.h>
using namespace std;
vector<int>b[10005],db[10005];//b 存边,db 反向存边
int v1[10005],v2[10005],v[10005];//v1 为能否到达终点,v2 为指向的边能否到达终点,v 用来找最短路时判重
struct Node{
int i,n;//节点编号及路径长度
};
queue<Node>q;
void dfs(int i){
for(int j=0;j<db[i].size();j++){
if(v1[db[i][j]]==0){
v1[db[i][j]]=1;
dfs(db[i][j]);
}
}
}
void bfs(int i,int t){
if(v2[i]==0){//特判起点
return;
}
v[i]=1;
q.push({i,0});
while(q.size()){
Node p=q.front();
q.pop();
if(p.i==t){//BFS 第一个找到的一定是最短路
cout<<p.n;
exit(0);//结束程序
}
for(int j=0;j<b[p.i].size();j++){
if(v2[b[p.i][j]] && v[b[p.i][j]]==0){
v[b[p.i][j]]=1;
q.push({b[p.i][j],p.n+1});
}
}
}
}
void main1(){
int n,m,u,v,s,t;
cin>>n>>m;
for(int i=0;i<m;i++){
cin>>u>>v;
b[u].push_back(v);
db[v].push_back(u);
}
cin>>s>>t;
v1[t]=1;
dfs(t);//从终点反向搜寻
for(int i=1;i<=n;i++){
v2[i]=1;
}
for(int i=1;i<=n;i++){
if(v1[i]==0){
for(int j=0;j<db[i].size();j++){
v2[db[i][j]]=0;//判断指向节点能否到达终点
}
}
}
bfs(s,t);
cout<<-1;//如果程序还没结束,说明找不到要求路径
}
signed main(){//个人风格
int t=1;
//cin>>t;
while(t--){
main1();
}
return 0;
}
```