浅谈高维莫队

lzqy_ · 2022-02-15 22:22:13 · 个人记录

$update \;2023:$ 补充高维回滚莫队 --------- 发现网上没有对于高维莫队的系统性整理，这里简单整理一下。笔者实力有限，内容较为浅显，欢迎在评论区指教。 # 目录 - ### 引入 - ### 实现 - **排序** - **块长与效率** - ### 习题 - ### 其他 - **最优性证明** - **优化** - **效率估算** - **高维回滚莫队** - ### 总结 ----------- # 引入莫队是什么？区间查询的说法其实并不准确，比如这道题： > 有 $q$ 组询问，每组询问为二元组 $(n,m)$，求 $\sum\limits_{i=1}^{n}{m \choose i}$ 的值。 $\\(0\leq n,m,q\leq10^5)

这一题的做法是莫队，考虑已知 (n,m) 的答案，推出 (n,m±1),(n±1,m) 的答案。由于与高维莫队无关，这里就不展开讲解了。

可以看出，莫队本质上解决并不是区间问题，而是由若干个可以快速移动指针组成的询问。

其中，最熟悉的普通莫队就是 2 维莫队，带修莫队就是 3 维莫队。

到这里，高维莫队就好理解了。

高维莫队指的是指针数量（维数）大于等于 3 的莫队算法。

实现

排序

（此处默认升序排序）

莫队的排序分为两种，按照所在块排序、按照位置排序。容易发现，只要有 2 维及以上按照位置排序，时间复杂度一定不优于 \text{O(n}^{\text 2}\text )。

（考虑按位置排序的最后两维的指针为 [1,n],[2,1],[3,n],[4,1],\dots，移动次数已经达到 \text{O(n}^\text{2}\text ) 级别）

因此高维莫队的排序方式为，前 (k−1) 维按所在块排序，后一维升序排列。

代码片段如下：

struct Question{
    int Item[K],Blank[K],id;
}q[N];
bool cmp(Question a,Question b){
    for(int i=1;i<k;i++)
        if(a.Blank[i]!=b.Blank[i])
            return a.Blank[i]<b.Blank[i];
        return a.Item[k]<b.Item[k];
}

块长与时间复杂度

手膜一下不难发现，块长继续取 n^\frac{1}{2} 肯定是不行的，考虑取不同的块长。

实际上，对于 k 维莫队，理论最优的块长为 O(n^\frac{k-1}{k})，此时最优时间复杂度为 O(kn^\frac{2k-1}{k})，严格优于暴力 O(kn^2)。

为了不影响阅读，关于高维莫队的最优性证明放在后文。

代码片段如下：

int main(){
    scanf("%d%d%d",&n,&k,&m);
    Blank_len=pow(n,double(k-1)/k);
    ......
}

习题

除去带修莫队，高维莫队很少会作为正解出现。因此可使用高维莫队的题目通常解法不唯一。

矩形计算

题目大意

给出一个 n\times m 的矩阵，每次询问一个子矩阵的权值。权值定义为 \sum\limits_{i=-\infty}^{\infty} p_i^2。\\其中，p_i 表示数字 i 在子矩阵中出现的次数。

应该是网上唯一正解是高维莫队的题目了qwq，感动（

这道题就是 P2709 的加强版，从序列变成了矩阵。按照 P2709 的方式移动即可，只不过多移动了两个指针。注询问给出的是对角线。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=210;
const int maxq=200010;
const int inf=INT_MAX;
int read(){
    int x=0,f=1;
    char c=getchar();
    for(;!(c>='0'&&c<='9');c=getchar())
        if(c=='-') f=-1;
    for(;c>='0'&&c<='9';c=getchar())
        x=(x<<1)+(x<<3)+c-'0';
    return x*f; 
}
struct Que{
    int l[2],r[2];
    int bl[2],br[2];
    int id;
}q[maxq];
bool cmp(Que a,Que b){
    if(a.bl[0]^b.bl[0]) return a.bl[0]<b.bl[0];
    if(a.br[0]^b.br[0]) return a.br[0]<b.br[0];
    if(a.bl[1]^b.bl[1]) return a.bl[1]<b.bl[1];
    return ((a.bl[0]+a.br[0]+a.bl[1])&1)?a.r[1]<b.r[1]:a.r[1]>b.r[1];
}
map<int,int>H;
int b[maxn*maxn]; 
int a[maxn][maxn];
ll ans[maxq];
int l[2],r[2];
int Tap[maxn*maxn];
int n,m,Q,qn; 
int main(){
    int val=0,cnt=0;
    n=read(),m=read();
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            a[i][j]=read(),b[++cnt]=a[i][j];
    sort(b+1,b+cnt+1),b[0]=-inf;
    for(int i=1;i<=cnt;i++)
        if(b[i]^b[i-1]) H[b[i]]=++val;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            a[i][j]=H[a[i][j]];
    Q=read(),qn=max(n,m)*1.0/pow(Q,0.25);
    if(!qn) qn=29;//注意这一段,不加会在#20 RE
    for(int i=1;i<=Q;i++){
        q[i].l[0]=read(),q[i].l[1]=read();
        q[i].r[0]=read(),q[i].r[1]=read();
        if(q[i].l[0]>q[i].r[0]) swap(q[i].l[0],q[i].r[0]);
        if(q[i].l[1]>q[i].r[1]) swap(q[i].l[1],q[i].r[1]);
        q[i].bl[0]=(q[i].l[0]-1)/qn+1;
        q[i].br[0]=(q[i].r[0]-1)/qn+1;
        q[i].bl[1]=(q[i].l[1]-1)/qn+1;
        q[i].br[1]=(q[i].r[1]-1)/qn+1;
        q[i].id=i;
    }
    sort(q+1,q+1+Q,cmp);
    l[0]=l[1]=1;
    ll sum=0;
    for(int i=1;i<=Q;i++){
        while(l[0]>q[i].l[0]){
            l[0]--;
            for(int j=l[1];j<=r[1];j++) 
                Tap[a[l[0]][j]]++,sum+=(Tap[a[l[0]][j]]*2-1);
        }
        while(r[0]<q[i].r[0]){
            r[0]++;
            for(int j=l[1];j<=r[1];j++) 
                Tap[a[r[0]][j]]++,sum+=(Tap[a[r[0]][j]]*2-1);
        }

        while(l[1]>q[i].l[1]){
            l[1]--;
            for(int j=l[0];j<=r[0];j++) 
                Tap[a[j][l[1]]]++,sum+=(Tap[a[j][l[1]]]*2-1);
        }
        while(r[1]<q[i].r[1]){
            r[1]++;
            for(int j=l[0];j<=r[0];j++) 
                Tap[a[j][r[1]]]++,sum+=(Tap[a[j][r[1]]]*2-1);
        }
        while(l[0]<q[i].l[0]){
            for(int j=l[1];j<=r[1];j++) 
                sum-=(Tap[a[l[0]][j]]*2-1),Tap[a[l[0]][j]]--;
            l[0]++;
        }
        while(r[0]>q[i].r[0]){
            for(int j=l[1];j<=r[1];j++) 
                sum-=(Tap[a[r[0]][j]]*2-1),Tap[a[r[0]][j]]--;
            r[0]--; 
        }
        while(l[1]<q[i].l[1]){
            for(int j=l[0];j<=r[0];j++) 
                sum-=(Tap[a[j][l[1]]]*2-1),Tap[a[j][l[1]]]--;
            l[1]++;
        }
        while(r[1]>q[i].r[1]){
            for(int j=l[0];j<=r[0];j++) 
                sum-=(Tap[a[j][r[1]]]*2-1),Tap[a[j][r[1]]]--;
            r[1]--;
        }
        ans[q[i].id]=sum;
    }
    for(int i=1;i<=Q;i++)
        printf("%lld\n",ans[i]);
    return 0;
}

本题较卡常数，使用的优化后文有介绍。

[SNOI2017]一个简单的询问

题目大意

给出长度为一个 n 的序列 a，每次询问 \sum\limits_{x=0}^{\infty}get(l_1,r_1,x)\times get(l_2,r_2,x) 的值。\\ 其中，get(l,r,x) 表示数字 x 在 [l,r] 区间出现的次数。

考虑与一般解法不同的高维莫队的解法。

显然 l_1,r_1,l_2,r_2 都可以实现 O(1) 移动，所以直接用 4 维莫队实现即可。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=50010;
inline int read(){
    int x=0;
    char c=getchar();
    for(;!(c>='0'&&c<='9');c=getchar());
    for(;c>='0'&&c<='9';c=getchar())
        x=(x<<1)+(x<<3)+c-'0';
    return x;
}
struct Que{
    int l[2],r[2],id;
    int bl[2],br[2];
}q[maxn];
bool cmp(Que a,Que b){
    if(a.bl[0]^b.bl[0]) return a.bl[0]<b.bl[0];
    if(a.br[0]^b.br[0]) return a.br[0]<b.br[0];
    if(a.bl[1]^b.bl[1]) return a.bl[1]<b.bl[1];
    return a.r[1]<b.r[1];
}
int Tap[maxn][2],a[maxn];
ll ans[maxn];
int n,m,qn,l[2],r[2];
void Add(int k,int i,ll &sum){Tap[a[i]][k]++,sum+=Tap[a[i]][k^1];}
void Del(int k,int i,ll &sum){Tap[a[i]][k]--,sum-=Tap[a[i]][k^1];} 
int main(){
    n=read(),qn=pow(n,0.75);
    for(int i=1;i<=n;i++)
        a[i]=read();
    m=read();
    for(int i=1;i<=m;i++){
        q[i].l[0]=read(),q[i].r[0]=read();
        q[i].l[1]=read(),q[i].r[1]=read();
        q[i].bl[0]=(q[i].l[0]-1)/qn+1;
        q[i].br[0]=(q[i].r[0]-1)/qn+1;
        q[i].bl[1]=(q[i].l[1]-1)/qn+1;
        q[i].br[1]=(q[i].r[1]-1)/qn+1;
        q[i].id=i;
    }
    sort(q+1,q+1+m,cmp);
    ll sum=0;
    l[0]=l[1]=1;
    for(int i=1;i<=m;i++){
        for(int j=0;j<2;j++){
            while(l[j]>q[i].l[j]) Add(j,--l[j],sum);
            while(r[j]<q[i].r[j]) Add(j,++r[j],sum);
            while(l[j]<q[i].l[j]) Del(j,l[j]++,sum);
            while(r[j]>q[i].r[j]) Del(j,r[j]--,sum);
        }
        ans[q[i].id]=sum;
    }
    for(int i=1;i<=m;i++) printf("%lld\n",ans[i]);
    return 0;
}

时间复杂度 O(n^{\frac{7}{4}})，吸口氧才能过。

[AHOI2013]作业

题目大意

给出长度为一个 n 的序列 a，区间 [l,r] 中数值在 [a,b] 中的种类数与总数。\\n,m\leq10^5

显然的普通莫队套值域分块。但四维莫队也是可做的。

若 [a,b] 不变，则 l,r 都可以实现 O(1) 移动；若 [l,r] 不变，则 a,b 也可以实现 O(1) 移动。所以直接暴力移动四个指针 l,r,a,b 即可。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=100010;
const int maxm=100010;
inline int read(){
    int x=0;
    char c=getchar();
    for(;!(c>='0'&&c<='9');c=getchar());
    for(;c>='0'&&c<='9';c=getchar())
        x=(x<<1)+(x<<3)+c-'0';
    return x;
}
struct Que{
    int l[2],r[2],id;
}q[maxm];
int Tap[maxn],a[maxn];
pair<int,int>ans[maxn];
int Bl[maxn];
int n,m,qn,l[2],r[2];
bool cmp(Que a,Que b){
    if(Bl[a.l[0]]^Bl[b.l[0]]) return Bl[a.l[0]]<Bl[b.l[0]];
    if(Bl[a.r[0]]^Bl[b.r[0]]) return Bl[a.r[0]]<Bl[b.r[0]];
    if(Bl[a.l[1]]^Bl[b.l[1]]) return Bl[a.l[1]]<Bl[b.l[1]];
    return a.r[1]<b.r[1];
}
int main(){
    n=read(),m=read();
    qn=pow(n,0.75);
    for(int i=1;i<=n;i++)
        a[i]=read(),Bl[i]=(i-1)/qn+1;
    for(int i=1;i<=m;i++){
        q[i].l[0]=read(),q[i].r[0]=read();
        q[i].l[1]=read(),q[i].r[1]=read();
        q[i].id=i;
    }
    sort(q+1,q+1+m,cmp);
    int sum1=0,sum2=0;
    l[0]=l[1]=1;
    for(int i=1;i<=m;i++){
        while(l[0]>q[i].l[0]){
            --l[0],Tap[a[l[0]]]++;
            sum2+=(a[l[0]]>=l[1]&&a[l[0]]<=r[1]);
            sum1+=(a[l[0]]>=l[1]&&a[l[0]]<=r[1]&&Tap[a[l[0]]]==1);
        } 
        while(r[0]<q[i].r[0]){
            ++r[0],Tap[a[r[0]]]++;
            sum2+=(a[r[0]]>=l[1]&&a[r[0]]<=r[1]);
            sum1+=(a[r[0]]>=l[1]&&a[r[0]]<=r[1]&&Tap[a[r[0]]]==1);
        } 
        while(l[0]<q[i].l[0]){
            Tap[a[l[0]]]--;
            sum2-=(a[l[0]]>=l[1]&&a[l[0]]<=r[1]);
            sum1-=(a[l[0]]>=l[1]&&a[l[0]]<=r[1]&&Tap[a[l[0]]]==0);
            l[0]++;
        } 
        while(r[0]>q[i].r[0]){
            Tap[a[r[0]]]--;
            sum2-=(a[r[0]]>=l[1]&&a[r[0]]<=r[1]);
            sum1-=(a[r[0]]>=l[1]&&a[r[0]]<=r[1]&&Tap[a[r[0]]]==0);
            r[0]--;
        } 
        while(l[1]>q[i].l[1]) sum1+=(bool)Tap[--l[1]],sum2+=Tap[l[1]];
        while(r[1]<q[i].r[1]) sum1+=(bool)Tap[++r[1]],sum2+=Tap[r[1]];
        while(l[1]<q[i].l[1]) sum1-=(bool)Tap[l[1]],sum2-=Tap[l[1]++];
        while(r[1]>q[i].r[1]) sum1-=(bool)Tap[r[1]],sum2-=Tap[r[1]--];
        ans[q[i].id]=make_pair(sum2,sum1);
    }
    for(int i=1;i<=m;i++) printf("%d %d\n",ans[i].first,ans[i].second);
    return 0;
}

时间复杂度 O(n^{\frac{7}{4}})，也要开 \text{O2}。

[NOI2020] 时代的眼泪

题目大意

给出一个 n\times n 的矩阵，每行每列恰好有一个点。m 组询问，求一个子矩阵内包含多少个点对 \{(x_1,y_1),(x_2,y_2)\} 满足 x_1\le x_2,y_1\le y_2。

作为 NOID1T3，用高维莫队肯定是无法直接通过此题的，但是能取得不错的分数。

发现询问的子矩阵本质上是四个指针，考虑四维莫队。

每次指针移动时，都有可能在询问矩阵中新增/减一个点。显然该点的横/纵坐标有一个是询问矩阵中的极值，所以只需要维护另一坐标的区间和即可。

四维莫队套两个BIT，时间复杂度 O(n^{\frac{7}{4}}\log n)，但由于这只 \log 跑不满且是时限5s，所以有不错的效率。

特判一下 c_{1,i}=1,c_{2,i}=n 的二维莫队部分分，总共得分 64pt，属于比较优秀的暴力。


#include<bits/stdc++.h>
#define ll long long 
#define il inline
using namespace std;
const int maxn=200010;
il int read(){
    int x=0;
    char c=getchar();
    for(;!(c>='0'&&c<='9');c=getchar());
    for(;c>='0'&&c<='9';c=getchar())
        x=(x<<1)+(x<<3)+c-'0';
    return x;
}
int n,m,qn;
int Tree1[maxn],Tree2[maxn];
int Lx[maxn],Ly[maxn];
ll ans[maxn];
struct Que{
    int xl,xr,yl,yr,id;
    int bxl,bxr,byl;
}q[maxn];
il bool cmp(Que a,Que b){
    if(a.bxl^b.bxl) return a.bxl<b.bxl;
    if(a.bxr^b.bxr) return a.bxr<b.bxr;
    if(a.byl^b.byl) return a.byl<b.byl;
    return (a.bxl+a.bxr+a.byl&1)?a.yr<b.yr:a.yr>b.yr;
}
il void Add1(int k,int x){for(;k<=n;k+=k&-k)Tree1[k]+=x;}
il int Sum1(int k,int sum=0){for(;k;k-=k&-k)sum+=Tree1[k];return sum;}
il void Add2(int k,int x){for(;k<=n;k+=k&-k)Tree2[k]+=x;}
il int Sum2(int k,int sum=0){for(;k;k-=k&-k)sum+=Tree2[k];return sum;}
int main(){
    int x;
    n=read(),m=read();
    qn=pow(m,3.0/4);
    bool fl=1;
    for(int i=1;i<=n;i++)
        x=read(),Lx[i]=x,Ly[x]=i;
    for(int i=1;i<=m;i++){
        q[i].xl=read(),q[i].xr=read();
        q[i].yl=read(),q[i].yr=read();
        fl&=(q[i].yl==1&&q[i].yr==n);
    }
    if(fl) qn=sqrt(n);
    //这是性质A的特判,只需要改块长即可
    for(int i=1;i<=m;i++){
        q[i].bxl=(q[i].xl-1)/qn+1;
        q[i].bxr=(q[i].xr-1)/qn+1;
        q[i].byl=(q[i].yl-1)/qn+1;
        q[i].id=i;
    }sort(q+1,q+1+m,cmp);
    int xl=1,yl=1,xr=0,yr=0,tot=0;ll sum=0;
    for(int i=1;i<=m;i++){
        //Add
        while(xl>q[i].xl){
            --xl;
            if(Lx[xl]>=yl&&Lx[xl]<=yr){
                Add1(xl,1),Add2(Lx[xl],1),tot++;
                sum+=tot-Sum2(Lx[xl]);
            }
        }
        while(xr<q[i].xr){
            ++xr;
            if(Lx[xr]>=yl&&Lx[xr]<=yr){
                Add1(xr,1),Add2(Lx[xr],1),tot++;
                sum+=Sum2(Lx[xr]-1);
            }
        }
        while(yl>q[i].yl){
            --yl;
            if(Ly[yl]>=xl&&Ly[yl]<=xr){
                Add1(Ly[yl],1),Add2(yl,1),tot++;
                sum+=tot-Sum1(Ly[yl]);
            }
        }
        while(yr<q[i].yr){
            ++yr;
            if(Ly[yr]>=xl&&Ly[yr]<=xr){
                Add1(Ly[yr],1),Add2(yr,1),tot++;
                sum+=Sum1(Ly[yr]-1);
            }
        }
        //Del
        while(xl<q[i].xl){
            if(Lx[xl]>=yl&&Lx[xl]<=yr){
                sum-=tot-Sum2(Lx[xl]);
                Add1(xl,-1),Add2(Lx[xl],-1),tot--;
            }
            xl++;
        }
        while(xr>q[i].xr){
            if(Lx[xr]>=yl&&Lx[xr]<=yr){
                sum-=Sum2(Lx[xr]-1);
                Add1(xr,-1),Add2(Lx[xr],-1),tot--;
            }
            xr--;
        }
        while(yl<q[i].yl){
            if(Ly[yl]>=xl&&Ly[yl]<=xr){
                sum-=tot-Sum1(Ly[yl]);
                Add1(Ly[yl],-1),Add2(yl,-1),tot--;
            }
            yl++;
        }
        while(yr>q[i].yr){
            if(Ly[yr]>=xl&&Ly[yr]<=xr){
                sum-=Sum1(Ly[yr]-1);
                Add1(Ly[yr],-1),Add2(yr,-1),tot--;
            }
            yr--;
        }
        ans[q[i].id]=sum;
    }
    for(int i=1;i<=m;i++) 
        printf("%lld\n",ans[i]);
    return 0;
}

其他

最优性证明

填一下前文的坑。

设 k 维莫队的块长为 S，询问次数与值域都为 n（即默认 n,m 同阶，不同阶的情况在 优化 部分有提及）。

前文证明过，高维莫队的排序方式为，前 (k-1) 维按所在块排序，后一维按位置排列。

考虑此时莫队的时间复杂度：

对于前 (k-1) 的 \frac{n^{k-1}}{S^{k-1}} 种所在块状态，最后一维升序，所以最多移动 n 步，总共 \frac{n^k}{S^{k-1}} 步。
因为按照所在块排序，前 (k-1) 维每维最多移动 nS 步，总共 (k-1)nS 步（此处证明详见普通莫队的时间复杂度证明）。

所以 k 维莫队的时间复杂度为：

\frac{n^k}{S^{k-1}}+(k-1)nS

=n\times(\frac{n^{k-1}}{S^{k-1}}+(k-1)S)

求当 S 取何值时，该式最小。

设 F(S)=\frac{n^{k-1}}{S^{k-1}}+(k-1)S,a=n^{k-1}，求导得：

F'(S)=-a(k-1)S^{-k}+k-1

-a(k-1)S^{-k}+k-1=0

-\frac{1}{S^k}a(k-1)+k-1=0

\frac{1}{S^k}=\frac{k-1}{a(k-1)}

S^k=a,S=a^{\frac{1}{k}}=n^{\frac{k-1}{k}}

所以当块长取 n^{\frac{k-1}{k}} 时，最优时间复杂度为：

n\times(n^{\frac{k-1}{k}}+(k-1)n^{\frac{k-1}{k}})

即 \text{O(kn}^{\frac{\text{2k-1}}{\text k}}\text )。

当 n,k 为正整数时，该时间复杂度严格优于暴力 \text{O(kn}^\text{2}\text )。

优化

作为 ~~优雅的暴力~~ 通常情况下的非正解做法，卡常技巧是必须的。由于笔者实力有限，这里主要讲的是普通莫队优化的推广。

以 [SNOI2017]一个简单的询问 为例，这是未加优化的 4 维莫队（代码为上文示例）：

总用时 2.87s，最大用时 576ms。

奇偶优化

相信这个优化大家都很熟悉，这里就不赘述了。唯一需要注意的是，奇偶优化中的 奇偶 指的是 前 (k-1) 维所在块之和奇偶性。

代码片段如下：

bool cmp(Que a,Que b){
    if(a.bl[0]^b.bl[0]) return a.bl[0]<b.bl[0];
    if(a.br[0]^b.br[0]) return a.br[0]<b.br[0];
    if(a.bl[1]^b.bl[1]) return a.bl[1]<b.bl[1];
    return ((a.bl[0]+a.br[0]+a.bl[1])&1)?a.r[1]<b.r[1]:a.r[1]>b.r[1];
}

评测结果：

总用时 2.51s，最大用时 499ms。

块长

普通莫队的块长有两种，\sqrt n 和 \frac{n}{\sqrt{m}}。该结论是推广到 k 维莫队的，具体来说，k 维莫队的块长可以取 n^{\frac{k-1}{k}} 和 \frac{n}{\sqrt[k]{m}}，前者时间复杂度为 O(k(n+m)n^\frac{k-1}{k})，后者为 O(knm^\frac{k-1}{k})，n,m 同阶时复杂度相同。进行微调可能会有更多的优化。通过测试，本题块长取 \frac{n}{\sqrt[k]{m}}\times 1.17 时最优，评测结果如下：

总用时 2.82s，最大用时 567ms。块长调整的作用在本题中不明显，但对于 矩形计算 一类 n,m(q) 不同阶的题目来说，是非常有效的。

常数优化

高维莫队的时间复杂度瓶颈在于调用了 n^{\frac{2k-1}{k}} 次 Add 和 Del 函数。而函数调用的常数很大。将两个函数写在主函数中，会有较好的效率提升（这个方法同样适用于普通莫队，但效率提升不如高维莫队明显）。

评测结果：

总用时 1.60s，最大用时 294ms，是三种优化中最有效的。

结合三种优化：

总用时 1.27s，最大用时 259ms。总用时减少 1.22s，最大用时减少 240ms。

效率估算

注：为了方便，暴力与莫队都按照每秒跑 5\times 10^8 来估算，实际上打满优化的莫队常数会更优。

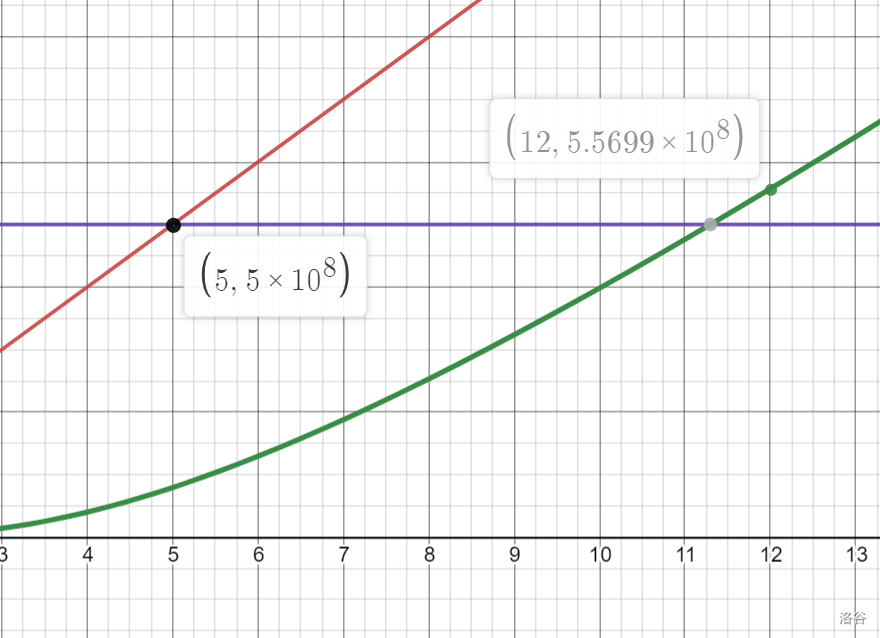![](https://cdn.luogu.com.cn/upload/image_hosting/ymkgswb0.png) 暴力正好可以跑到 $k=5$，而高维莫队的表现十分优秀，$5\times 10^8$ 的范围内最多可以跑到 $k=11$（$11$ 维莫队），但实际上是可以做到 $k=12$ 的，运算次数也只有 $5.5699\times10^8
。
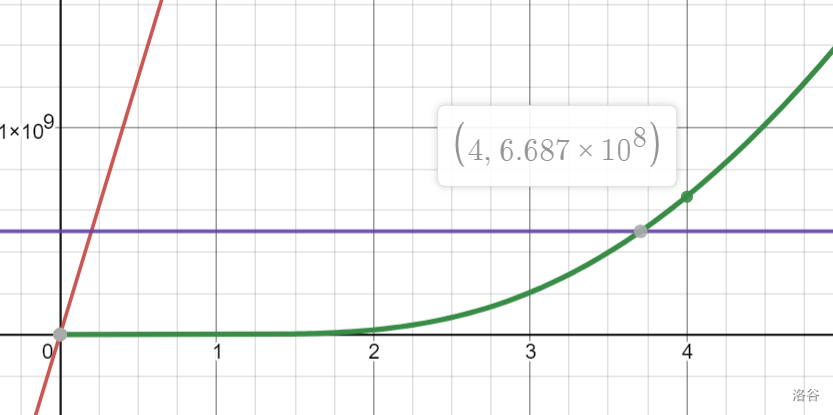![](https://cdn.luogu.com.cn/upload/image_hosting/kaspfrov.png) 暴力已经跑不动，莫队在 $5\times 10^8$ 的范围内最多可以跑到 $k=3$（$3$ 维莫队）。优化后可以卡过 $k=4$，运算次数约为 $6.687\times10^8$。
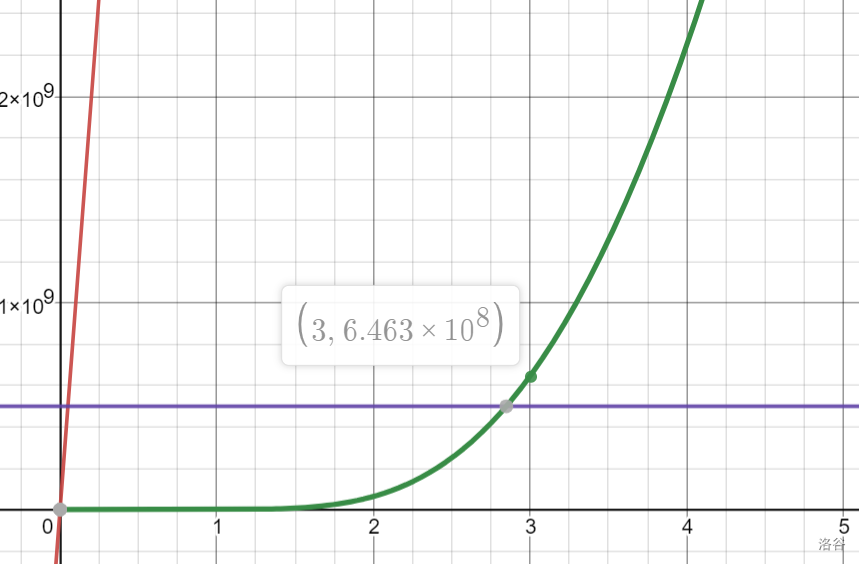![](https://cdn.luogu.com.cn/upload/image_hosting/vk6esa23.png) 暴力肯定还是过不去的，但莫队在 $5\times 10^8$ 的范围内也只能达到 $k=2$ ，即 $2$ 维莫队（普通莫队）。卡一卡最多跑到 $k=3$ （$3$ 维莫队），运算次数约为 $6.463\times10^8$。

高维回滚莫队

这一类题不能把询问点看成单纯的指针，因为 回滚 是具有区间性质的。

CF1767F

浅谈高维莫队

实现

排序

块长与时间复杂度

习题

矩形计算

[SNOI2017]一个简单的询问

[AHOI2013]作业

[NOI2020] 时代的眼泪

其他

最优性证明

优化

效率估算

高维回滚莫队

CF1767F