splay
20213116lyd
·
·
个人记录
BST
先介绍二叉搜索树BST(Binary Search Tree),性质:
$2.$ 右子树的所有结点权值都大于于当前结点
$3.$ 中序遍历是递增序列
# 平衡树
当BST退化成一条链的时候,我们查询就变成了 $O(n^2)$,容易被卡掉,于是我们需要一种数据结构在维护序列的同时,保持树的深度为 $log(n)$,于是我们把它叫做平衡树。
# splay
不妨设现在有这样一棵 $splay$:(图片来源于[blog](https://www.cnblogs.com/cjyyb/p/7499020.html))
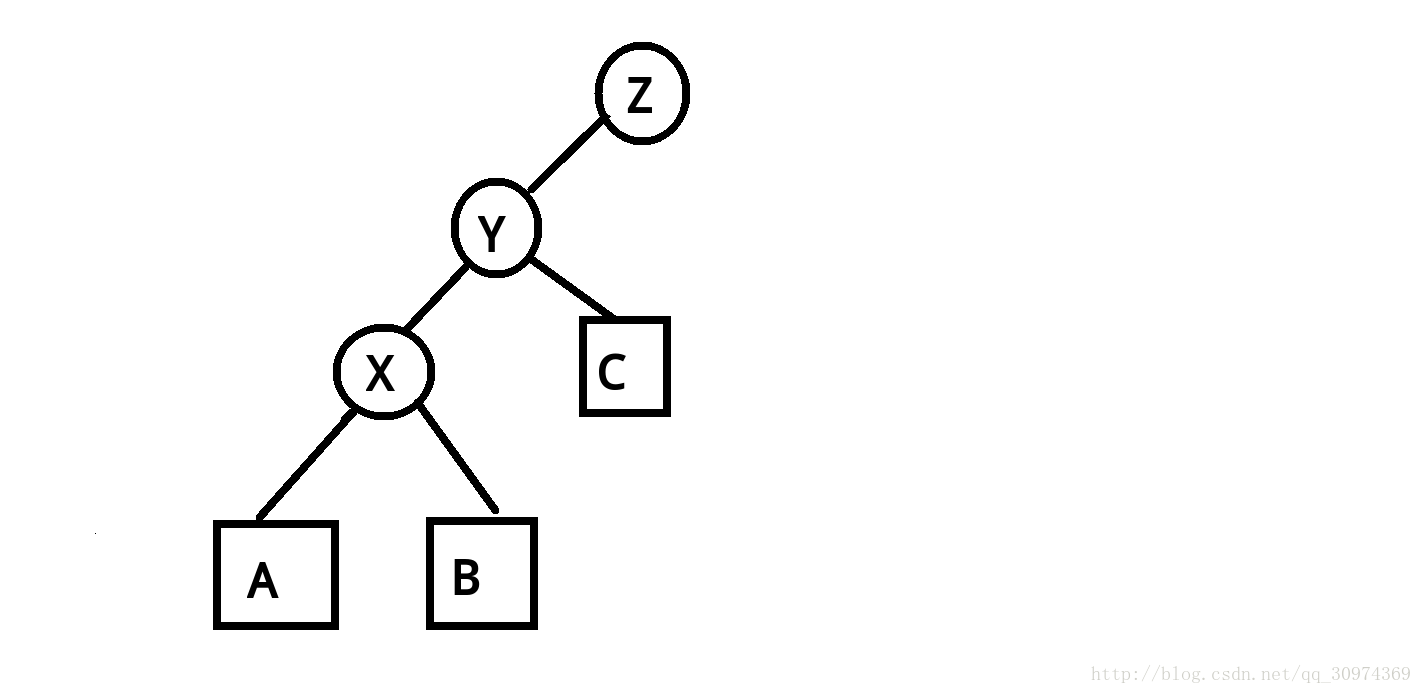
根据 $BST$ 得特点,可得:$z>C>y>B>x>A
假设我们现在想要让 x 往上爬一层该如何做到呢
即我们的 x 现在要到 y 这个位置上去,既然 x 上去了,那么 y 就会往下走一层,想要依然满足 BST 的性质,就需要 y 做 x 的右儿子。再更新牵连到的结点,给个图片体会一下。
就像这样,多举几个例子就可以发现规律,这里不过多阐述 就是懒而已。
void update(ino x) {
t[x].siz = t[t[x].ch[0]].siz + t[t[x].ch[1]].siz + t[x].cnt;
}
void rotate(ino x) {
ino y = t[x].fa,z = t[y].fa,w = (t[y].ch[1] == x);
t[z].ch[t[z].ch[1]==y] = x;
t[x].fa = z;
t[y].ch[w] = t[x].ch[w^1];
t[t[x].ch[w^1]].fa = y;
t[x].ch[w^1] = y;
t[y].fa = x;
update(y); update(x);
}
关于树的定义我们稍后再讲,因为——现在我们有了 rotate 操作后任然会被卡。例如 :
它形成了一条类似链,但我们仅靠反转 x 是不够的,这时我们只需要反转 y 就行了 读者自证不难
接下来就是 splay 操作:挺好理解的,就是一直将 x 结点往上面反转,直到它成为 ex 的儿子。
void splay(ino x,ino ex) {
for(;t[x].fa ^ ex; rotate(x)) {
ino y = t[x].fa,z = t[y].fa;
if(z ^ ex)
t[y].ch[1]^x^t[z].ch[1]^y ? rotate(x) : rotate(y);
}
if(!ex) root = x;
}
$0.$ 定义 $splay
看代码
struct node {
ino fa,val,cnt,siz,ch[2];
fa -> 父亲 val -> 权值 cnt -> 这个结点有多少个权值为val的数,siz -> 子树结点个数 ch[0] -> 左儿子 ch[1] -> 右儿子
}t[1000005];
ino n,root,tot;
由于 $x$ 的大小是给定的,我们只需要从根一直往下面走,如果比当前结点大就走它的右边否则就走它的左边,直到走到尽头或有一个结点的权值等于它,如果已经有了,就直接 $cnt++$,没有就新建一个。
```cpp
void ins(ino x) {
ino p = root,fa = 0;
while(p && x ^ t[p].val) {
fa = p;
p = t[p].ch[x > t[p].val];
}
if(p) t[p].cnt++;
else {
p = (++tot);
if(fa) t[fa].ch[x > t[fa].val] = p;
t[p].fa = fa;
t[p].siz = t[p].cnt = 1;
t[p].ch[0] = t[p].ch[1] = 0;
t[p].val = x;
}
splay(p,0); //最后再把翻到根节点去,使其平衡。
}
```
$2.$ 查询 $x$ 数的排名(排名定义为比当前数小的数的个数 $+1$ )
我们依然从根结点一直往下走,直到找到 $x$ 为止。
```cpp
void find(ino x) {
ino p = root;
if(!p) return;
while(t[p].ch[x > t[p].val] && x ^ t[p].val)
p = t[p].ch[x > t[p].val];
splay(p,0); ////最后再把翻到根节点去,好查询。
}
```
$3.$ 求 $x$ 的前驱(前驱定义为小于 $x$ ,且最大的数)
$4.$ 求 $x$ 的后继(后继定义为大于 $x$ ,且最小的数)
为什么把他们放一起讲呢,因为他们可以一起写,先找到 $x$ 的位置,再分四种情况讨论就行了,不再过多阐述 ~~懒~~
```cpp
ino _next(ino x,ino e) {
find(x);
ino p = root;
if(t[p].val > x && e) return p;
if(t[p].val < x && !e) return p;
p = t[p].ch[e];
while(t[p].ch[e^1]) p = t[p].ch[e^1];
return p;
}
```
$5.$ 删除 $x$ 数(若有多个相同的数,因只删除一个)
先把 $x$ 的前驱翻为根,再把 $x$ 的后驱翻到前驱下面,这样你会发现,根据 $splay$ 的性质,后驱就只有 $x$ 这一个儿子作为叶子结点,我们就可以直接删除了
```cpp
void erase(ino x) {
ino l = _next(x,0),r = _next(x,1);
splay(l,0); splay(r,l);
ino lkid = t[r].ch[0];
if(t[lkid].cnt > 1) t[lkid].cnt--,splay(lkid,0);
else t[r].ch[0] = 0;
}
```
$6.$ 查询排名为 $x$ 的数
就像主席树那样查询就好了,看 $x$ 是否大于当前节点左儿子的结点数,如果小于就什么 $x$ 在左边,否则在右边,具体细节看代码:
```cpp
ino p = root;
if(t[p].siz < x) return 0;
while(1) {
ino y = t[p].ch[0];
if(x > t[y].siz + t[p].cnt) {
x -= (t[y].siz+t[p].cnt);
p = t[p].ch[1];
}
else if(t[y].siz >= x) p = y;
else return t[p].val;
}
```
最后附上完整代码:
```cpp
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
typedef int ino;
void sr(ino &x) {
ino f=1;x=0;char s=getchar();
while(s>'9'||s<'0') {if(s=='-') f=-1;s=getchar();}
while(s>='0'&&s<='9') {x=x*10+s-'0';s=getchar();}
x *= f;
}
struct node {
ino fa,val,cnt,siz,ch[2];
}t[1000005];
ino n,root,tot;
void update(ino x) {
t[x].siz = t[t[x].ch[0]].siz + t[t[x].ch[1]].siz + t[x].cnt;
}
void rotate(ino x) {
ino y = t[x].fa,z = t[y].fa,w = (t[y].ch[1] == x);
t[z].ch[t[z].ch[1]==y] = x;
t[x].fa = z;
t[y].ch[w] = t[x].ch[w^1];
t[t[x].ch[w^1]].fa = y;
t[x].ch[w^1] = y;
t[y].fa = x;
update(y); update(x);
}
void splay(ino x,ino ex) {
for(;t[x].fa ^ ex; rotate(x)) {
ino y = t[x].fa,z = t[y].fa;
if(z ^ ex)
t[y].ch[1]^x^t[z].ch[1]^y ? rotate(x) : rotate(y);
}
if(!ex) root = x;
}
void find(ino x) {
ino p = root;
if(!p) return;
while(t[p].ch[x > t[p].val] && x ^ t[p].val)
p = t[p].ch[x > t[p].val];
splay(p,0);
}
void ins(ino x) {
ino p = root,fa = 0;
while(p && x ^ t[p].val) {
fa = p;
p = t[p].ch[x > t[p].val];
}
if(p) t[p].cnt++;
else {
p = (++tot);
if(fa) t[fa].ch[x > t[fa].val] = p;
t[p].fa = fa;
t[p].siz = t[p].cnt = 1;
t[p].ch[0] = t[p].ch[1] = 0;
t[p].val = x;
}
splay(p,0);
}
ino _next(ino x,ino e) {
find(x);
ino p = root;
if(t[p].val > x && e) return p;
if(t[p].val < x && !e) return p;
p = t[p].ch[e];
while(t[p].ch[e^1]) p = t[p].ch[e^1];
return p;
}
void erase(ino x) {
ino l = _next(x,0),r = _next(x,1);
splay(l,0); splay(r,l);
ino lkid = t[r].ch[0];
if(t[lkid].cnt > 1) t[lkid].cnt--,splay(lkid,0);
else t[r].ch[0] = 0;
}
ino kth(ino x) {
ino p = root;
if(t[p].siz < x) return 0;
while(1) {
ino y = t[p].ch[0];
if(x > t[y].siz + t[p].cnt) {
x -= (t[y].siz+t[p].cnt);
p = t[p].ch[1];
}
else if(t[y].siz >= x) p = y;
else return t[p].val;
}
}
int main() {
ino n;
sr(n);
ins(1e9); ins(-1e9);
ino x,y;
for(int i = 1;i <= n; ++i) {
sr(y); sr(x);
if(y == 1) ins(x);
else if(y == 2) erase(x);
else if(y == 3) {
find(x);
printf("%d\n",t[t[root].ch[0]].siz);
}
else if(y == 4) printf("%d\n",kth(x + 1));
else if(y == 5) printf("%d\n",t[_next(x,0)].val);
else printf("%d\n",t[_next(x,1)].val);
}
return 0;
}
```
## $splay$ 还有很多操作,但大部分都是基于以上操作,感觉是最自由的一个数据结构
# $end