快速傅里叶变换 FFT
SalN
·
·
算法·理论
一坑未填又开一坑。
yyc 的讲课速度我不能接受。
做不到两天速通网络流字符串反演fft。
总是听不懂,脑子要炸裂了捏 /wq
加法卷积 $C[k]=\sum_{i+j=k}A[i]B[j]$。
其实差不多就是两个 $x$ 进制的数相乘,只不过当前位的数不一定在 $[0,k)$ 罢了捏。
----
### 分治乘法
左右拆半分而治之,一次算 3 次。复杂度 $T(n)=O(n)+3T(n/2)$,解得 $T(n)=O(n^{\log_23)}=O(n^{1.585})$。
我们要算 $A$ 卷 $B$。我们弄 $A=A_0x^{\lfloor n/2\rfloor}+A_2,B=B_0x^{\lfloor m/2\rfloor}+B_2$ 以及 $A_1=A_0x^{\lfloor n/2\rfloor},A_2=B_0x^{\lfloor m/2\rfloor}$,换元大法好。
$$AB=(A_1+A_2)(B_1+B_2)$$
$$=A_1B_1+A_1B_2+A_2B_1+A_2B_2$$
$$=2(A_1B_1+A_2B_2)-(A_1-A_2)(B_1-B_2)$$
----
### FFT
把复数 $a+bi$ 看成平面直角坐标系中的点 $(a,b)$。
⌈ 模长 ⌋ 指的是点到原点的距离。 ⌈ 幅角 ⌋ 指的是横轴正半轴的射线绕原点逆时针转碰到点至少要转的角。
两个复数相乘,模长相乘,幅角相加。
$n$ 次单位根 $\omega_n=\cos(2\pi/n)+i\sin(2\pi/n)$,意思是 ⌈ 顺时针转 $1/n$ 圆周 ⌋。 那么 $\omega_n$ 的 $0$~$n-1$ 次幂 互不相同 & 均分单位圆。
----
求解 $C=AB$ 中的 $C$ 的大概的流程
+ **选数** 选定 $n$ 个数 $1,\omega_n,\omega_n^2,...,\omega_n^{n-1}$。
+ **DFT** 将多项式 $A(x)$ 视为函数,$x=t_0$ 的值即为 $A(x)$ 的点值。求出 $A,B$ 在 $x_i$ 处的点值。
+ **点积** 用算出来的点值得到 $C$ 的点值。
+ **IDFT** 用 $C$ 若干点值求出其所有系数。
----
#### DFT
给出 $A$,对 $k=0$~$n-1$ 求 $A(\omega_n^k)$。
分而治之,奇偶拆半(本质上是讨论余数合并)。
$$A(x)=A_0(x^2)+xA_1(x^2)$$
$$A(\omega_n^k)=A_0(\omega_n^{2k})+\omega_n^kA_1(\omega_n^{2k})$$
$$=A_0(\omega_{n/2}^k)+\omega_n^kA_1(\omega_{n/2}^k)$$
最后一步几何理解。复杂度很显然是 $O(n\log n)$ 捏。/youl/youl
----
#### IDFT
luogu 知名管理员 chen_zhe 曾经发过一个帖子:关于有一位人士提交了 ⌈ 输入一些数,输出一些符合题意的数 ⌋ 的题目翻译。显然这位人才领悟了算法竞赛的精髓(确信。
线性算法是一个系数矩阵。通过矩阵 $W$ 可以从数列 $X$ 生成另一个数列 $Y$,具体而言是 $Y[k]=\sum_{i=0}^{n-1}A[i]W[i,k]$。
记计算 $X$ 的线性算法为 $W(X)$,有性质 $W(X+Y)=W(X)+W(Y),W(tA)=tW(A)$ 捏。
康康 $A(\omega_n^k)=\sum_{i=0}^{n-1}A[i]\omega_n^{ik}$,可以发现 DFT 是一个线性算法,IDFT 就是要求这个的逆矩阵。

祂的逆矩阵的结论是什么捏(?
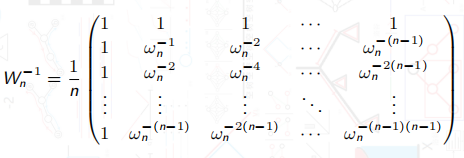
$IDFT(A)$ 相当于将数列 $A$ 构造为多项式,然后计算 $A(\omega_n^{-0}),A(\omega_n^{-1}),A(\omega_n^{-2}),...,,A(\omega_n^{-(n-1)})$。
有两个办法。op1,单位根改成 $\omega_n^{-1}$,跑 DFT。op2,注意到 $\omega_n^{-k}=\omega_n^{n-k}$,先跑一遍 DFT 再翻转。
----
#### 复域压缩优化
我们要算 $C=AB$。构造复多项式 $F(x)=A(x)+iB(x)$,则 $F^2(x)=A^2(x)-B^2(x)+2iA(x)B(x)$。算 $F^2$ 取出其虚部就能得到 $A(x)B(x)$ 的系数。这样可以把次数变少。
----
```cpp
#include<bits/stdc++.h>
#define db double
using namespace std;
inline int read() {
register char ch=0;
while(ch<48||ch>57) ch=getchar();
return ch-'0';
}
void write(int ch) {
if(ch<0) { ch=~(ch-1); putchar('-'); }
if(ch>9) write(ch/10);
putchar(ch%10+'0');
}
const db pi=acos(-1);
struct cp { db x, y; };
typedef const cp ccp;
cp operator+(ccp &a,ccp &b)
{ return (cp){a.x+b.x,a.y+b.y}; }
cp operator-(ccp &a,ccp &b)
{ return (cp){a.x-b.x,a.y-b.y}; }
cp operator*(ccp &a,ccp &b)
{ return (cp){a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x}; }
vector<cp> w[20];
void init(int m) {
for(int k=1; (1<<k)<=m; ++k) {
int n=(1<<k);
w[k].resize(n>>1);
for(int i=0; i<(n>>1); ++i)
w[k][i]=(cp){cos(2*i*pi/n),sin(2*i*pi/n)};
}
}
void dft(vector<cp> &f) {
if(f.size()==1) return;
int n=f.size();
vector<cp> f0, f1;
f0.resize(n>>1), f1.resize(n>>1);
for(int i=0; i<n; i+=2) f0[i>>1]=f[i];
for(int i=1; i<n; i+=2) f1[i>>1]=f[i];
dft(f0), dft(f1);
int id=0;
while((1<<id)<n) id++;
for(int k=0; k<(n>>1); ++k) {
cp tmp=w[id][k]*f1[k];
f[k]=f0[k]+tmp;
f[k+(n>>1)]=f0[k]-tmp;
}
}
void idft(vector<cp> &f) {
int n=f.size();
dft(f);
reverse(&f[1],&f[n]);
for(int i=0; i<n; ++i)
f[i].x/=n, f[i].y/=n;
}
signed main() {
int n, m, N=1;
scanf("%d%d", &n, &m);
while(N<=n+m) N<<=1;
init(N);
vector<cp> f;
f.resize(N);
for(int i=0; i<=n; ++i) f[i].x=read();
for(int i=0; i<=m; ++i) f[i].y=read();
dft(f);
for(int i=0; i<N; ++i) f[i]=f[i]*f[i];
idft(f);
for(int i=0; i<n+m+1; ++i)
write(f[i].y*0.5+0.1), putchar(' ');
return 0;
}
```