图论入门
Chtholly_L
·
·
个人记录
最近无论是大佬还是蒟蒻都在疯狂地写博客,
怎么能少的了我呢? hiahiahia
码字不易,码图不易,
所以
点个赞吧 QAQ
ps: 手欠把上传到洛谷的图片都给删了QMQ,又重新手画了一遍,更辛苦了。
另外
画图工具: Graph Editor
上传工具: 路过图床
First 什么是图:
- 图由点和边构成,一条边一定会连接两个点,两个点称为端点,许多的点和边组合在一起就成为了图,图的本质就是点和边的集合。
G=(V,E)
[](https://imgtu.com/i/WYdv7t)
[](https://imgtu.com/i/WYwC9S)
这两张图虽然看起来不一样,但是它们本质上是完全一样的,因为它们的点和边的关系是一样的,它们的连接关系是一样的。
* 图还有路径的定义。
就是从一个点到另一个点经过的路径,而有向图一般认为方向一样才算一条路径
* 图还有子集的定义。
图的子图指原图中的一个子集,这个子集也是一个图。
**图中点的度数指连接在这个点的边数。**
* 图还有图的直径、密度等定义,暂时学不到,更不会考到,就不说了。
---
## Second 图的分类:
* 图最基本的分类是有向图和无向图。
其中无向图表示图中的边是不区分方向的,可以从一个结点到其他的任何一个点。
有向图则不是,只能从特定的起点到终点。
* 另一个常见的分类是连通图和非连通图。
这两个都是针对无向图定义的。
即使一个图被分为两块,它们也是一个图,只不过是非连通的。
* 图还可分为带权图和无权图
[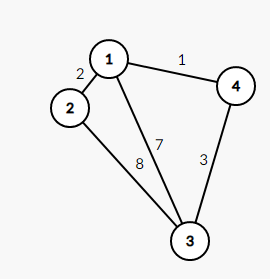](https://imgtu.com/i/WYwEBn)
这就是带权图。
可以把这四个点看成四个城市,边是高速公路,把权看做公路的长度(**只是一个示意,不是真的长度!**)
* 其次就是有向无环图,树,团,网络,仙人掌,线段树,珂朵莉树等等等。
这是有向无权图。
[](https://imgtu.com/i/WYwwge)
---
几个例子
[](https://imgtu.com/i/WYwb5V)
[](https://imgtu.com/i/WYwjv4)[](https://imgtu.com/i/WYwxKJ)
下面的两个图是上面的图的子图
[](https://imgtu.com/i/WYBqcF)
这个图的点二的度数为 $3$ 。
[](https://imgtu.com/i/WY06sJ)
这个图的点二的入度为 $1$ ,出度为 $2$ 。
---
## Second 图的存储:
* 可以分为 STL 型和数组型两类。
* **邻接矩阵**,**邻接链表**,**链式前向星**。
### ① 邻接矩阵:
这个存储方法很粗暴简单(~~很适合菜鸡~~)
**定义:** 对一个有 $N$ 个结点的图,邻接矩阵就是一个 $N \times N$ 的二维数组。它的每个元素都是 $0$ 或 $1$ 。如第 $i$ 行第 $j$ 列的元素为 $1$ ,则表示 $i$ 和 $j$ 之间有一条边。
**特点:** 无向图的邻接矩阵关于对角线对称(存图的时候记得给矩阵里两个方向的元素都赋为 $1$ ),如果图没有自环,那么对角线上的元素都为 $0$ 。一条边可能只出现一次,如 $1-2$ ,但矩阵里有两个元素 $(1,2)$ 和 $(2,1)$ 受到其影响。
代码实现(无向图):
```cpp
#include<iostream>
using namespace std;
int n,m;
int e[2100][2100];
int main(){
cin>>n>>m; //表示结点的个数和边的个数
int l,r;
for(int i=1;i<=m;i++){
cin>>l>>r; //连接的两个点
e[l][r]=1,e[r][l]=1;
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cout<<e[i][j]<<' ';
}
cout<<endl;
}
return 0;
}
```
---
### ② 邻接链表:
* 邻接链表就使用链表来存图。
邻接的意思就是储存一条边连接的两个结点作为信息。
邻接链表给每个结点分配一个链表,链表的链结中储存着两类信息,一类用于构成链表这个数据结构的信息,例如指向下一个链结或者上一个链结,另一类是关于边的信息,例如这条边的另一个端点是谁(一个端点已经确定,只需要存一个就够了)。
以下是一张图和它的邻接链表。
[](https://imgtu.com/i/WYBSSS)
1->2->4
2->3->1->4
3->2
4->1->2
代码实现:
```cpp
#include<iostream>
#include<cstdio>
using namespace std;
struct nds{
int y,nxt;
}e[2100];
//e是链结,y手边的下一端点,nxt是next,下一个链结的下标
int ltp =0,lk[110];
//ltp类似于栈的top ,用来随时 分配新的链结
//lk是link,lk[i]表示结点i的链表的第一个链结的下标
void ist(int x,int y){
//ist是insert,在链表钱插入一个链结(或者说往图里插入一条边)
//x和y表示要建立一个从x指向y的节点,无向图需要再建立反相边
e[++ltp]={y,lk[x]};
//让ltp+1,分配一个新连接,它的下一节点是y,下一个链结是lk[x]
//lk[x]也就是第一个链结,这个要结合下一步理解
lk[x]=ltp;
//让链表的第一个结点等于新分配的链结
e[++ltp]={x,lk[y]};
lk[y]=ltp;
//如果是无向图存图就需要给相反的的方向也插入一条边
//需要注意的是,无向图存储用的边数是输入的边数*2(易错点)
}
int main(){
cin>>n>>m;
int l,r;
for(int i=1;i<=m;i++){
cin>>l>>r;
ist(l,r);
}
for(int k=1;k<=n;k++){
cout<<k;
//输出结点标号
for(int i=lk[k];i;i=e[i].nxt){
//从k所在链的第一个链结开始,沿着下一个链结遍历
//直到遍历到头位置(下一个链结下标为0)
cout<<e[i].y;
//输出另一个端点的标号
}
cout<<endl;
}
return 0;
}
```
#### 差别
邻接矩阵的空间复杂度为 $O(n^2)
邻接链表的空间复杂度为 O(m)
邻接矩阵一般用于数据比较小的情况下,以及需要它的性质的时候(因为太容易爆炸了啊),因此邻接链表用的比较多,虽然很复杂,背过就行了 (doge) 。
Third 图的遍历:
图的遍历是指从一个(或多个)结点出发,沿着边遍历其他结点。由于图的结构不确定,也比较复杂,因此常采用搜索( dfs&bfs )的方法。
用邻接矩阵 dfs
bool f[2100];
void dfs(int x){
if(f[x])return ;
f[x]=true;
for(int i=1;i<=n;i++){
if(e[x][i])dfs(i)
}
}
用邻接链表 bfs
int q[2100],hd=0;
bool f[2100];
void(bfs){
q[hd=1]=1;
for(int k=1;k<=hd;k++){
for(int lk[q[k]];i;i=e[i].nxt){
if(!f[e[i].y]){
q[++hd]=e[i].y;
f[e[i].y]=true;
}
}
}
}
推荐几道例题:
P5318 查找文献
P3916 图的遍历
P2661 信息传递
P2296 寻找道路
P1330 封锁阳光大学
P2853 奶牛聚餐
P1341 无序字母对
じゃ、これで!