CF1163F
dbxxx
·
·
题解
删边最短路
你说得对,但是很遗憾,您上传的题解 CF1163F 未能通过审核。原因是 LaTeX 使用不符合规范(运算符) 。
这篇题解的特点
其实其他的题解都有几处证明跳跃的点。比如,怎么证明删边最短路只强制经过一条边就足够,而不需要强制经过两条,三条边呢?这个结论的证明并不如想象中简单,而且我想读者阅读完其它题解后也很难意识到这个结论只在 无向正权图 上成立,只要负权 / 零权 / 有向,这个结论就立刻失效了。
又比如,怎么证明“任何一条删边最短路和原最短路只共享一段前缀和一段后缀”?这个其它题解倒是给了很多证明,但是也相对跳跃。比如没有题解说明为什么删边最短路和原最短路的交点,在两条路线上出现的顺序相同。如果不说明这一点,很多题解的证明是失效的。比如:
还有一些题解中的语言模糊,有缺陷。比如“$1$ 到 $x$ 的最短路和 $1$ 到 $n$ 的最短路的最后一个交点”这种说法。无向图上任意两点间最短路径并不是唯一的,那请问“$1$ 到 $x$ 的最短路和 $1$ 到 $n$ 的最短路的最后一个交点”取的是哪两条最短路的交点呢?是任意的吗?似乎也不是,因为 $1$ 到 $n$ 的最短路是一定要钦定的。那 $1$ 到 $x$ 就是任意的吗?笔者通过简单推导发现似乎也不是如此。
总之,其他题解中一些语言过于模糊,一些证明过于跳跃,可能给您带来困难,那么本文就是尽量来解决这些困难的。
## 前言
删边最短路是一种科技,用于解决一类问题:
> 给定 **正权** 图 $G = (V, E)$。设 $n = |V|$,保证 $1$ 可达 $n$。
>
> 设 $\Delta(e)$ 为图 $G' = (V, E \setminus \{e\})$ 上 $1 \rightsquigarrow n$ 的最短路,若 $G'$ 上 $1$ 不可达 $n$ 则为 $+\infty$。
>
> 对每个 $e \in E$,求出 $\Delta(e)$。
>
> 点的编号不影响什么,源点和终点可以随便给,这里给 $1$ 和 $n$ 是为方便。
我将删边最短路称为科技,是因为删边最短路的整个流程逻辑链相对复杂,难以想到,重在积累。
所以本文只会描述删边最短路科技的过程以及必要的证明。
**前置知识:最短路树的定义与构建。**
最短路树在 OI 中的应用可比删边最短路这种科技要常用得多,如果还不了解推荐赶紧学习一下。
同时,删边最短路并不是一种非常常用的科技,笔者比较实用主义,所以:
**本文证明删边最短路正确性使用的推论,是按照在整个 OI 图论(不局限于删边最短路)上,尽可能有用来选取的,而不是按照用到的推论尽可能少,证明复杂度尽可能简单来选取的。**
后者的确有它的优势,但是我想,如果看完这篇文章只学到删边最短路和一些只能用来证明删边最短路的 adhoc 推论,那写这篇文章也没多大意义,毕竟删边最短路也没有多少习题。
## 无向图
即保证 $G$ 是无向的。
这里再加一个限制条件:$G$ 是连通图,可以简化讨论。
$G$ 不是连通图的情况:
- $1$ 和 $n$ 不连通:所有删边最短路都是 $+\infty$。
- $1$ 和 $n$ 连通:除了 $1$ 和 $n$ 所在连通块,其他联通块上的边删除后,$1$ 到 $n$ 的最短路就是原来的最短路。
所以只需要讨论 $1$ 和 $n$ 所在连通块的这一部分图了,因此只需讨论连通图上的删边最短路。
### 基础记号与约定
#### 约定
本文认为路径有向,虽然无向图上一条路径也可以反着走,不过我会将其看做是另一条方向相反的路径。
本文中,”最短路“和”最短路径“两种表述存在差异,前者指的是长度,后者指的是路径。
本文中,$u \rightsquigarrow v$ 指的是 $u$ 通过一些边(也可只有一条边)走到 $v$,而 $u \to v$ 指的是 $u$ 仅通过 $(u, v)$ 这一条边走到 $v$。
本文中,说一条路径 $X$ 为一条最短路径时,$X$ 的起点 $s$ 和终点 $t$ 一定是已知的,这句话的意思就是 $X$ 是 $s$ 到 $t$ 的若干条最短路径中的一条,只是省略了起点和终点而已。
#### 权值
$w(e)$ 代表边 $e$ 的权值,$w(u, v)$ 代表 $(u, v)$ 这条边的权值,$w(X)$,其中 $X$ 是一条路径,代表路径 $X$ 的总权值。
#### 路径的拼接
定义两条路径 $X$ 和 $Y$ 的合并运算 $X \oplus Y$。该运算需要使得 $X$ 的终点和 $Y$ 的起点是同一个点。
设 $X = x \rightsquigarrow y$,$Y = y \rightsquigarrow z$,则 $X \oplus Y$ 的结果 $Z$ 也是一条路径,其从 $x$ 出发,先走 $X$ 到达 $y$,再走 $Y$ 到达 $z$。
#### 子路径
对于一条简单路径 $X$ 和两个在 $X$ 上的点 $u$,$v$,并且 $X$ 先走到 $u$ 再走到 $v$,
定义 $X(u, v)$ 为 $X$ 这条路径中,从 $u$ 走到 $v$ 的这一部分子路径。
注意上面的 $u$ 可以等于 $v$,此时 $X(u, u)$ 这条子路径只有一个点 $u$,没有边。
#### 树上的路径
对于一棵树 $T$ 和两个在 $T$ 上的点 $u$,$v$,定义 $T(u, v)$ 为 $T$ 上从 $u$ 到 $v$ 的这一部分路径。
### 记号(与删边最短路具体做法相关)
设 $G = (V, E)$ 的 **以 $\boldsymbol 1$ 为根** 的 **任意一棵** 最短路树 $T = (V, E_{T})$。
设 $D(1, u)$ 表示 $T(1, u)$ 这条路径的总权值,即 $w(T(1, u))$。
简记 $P = T(1, n)$,$D = D(1, n)$。
因为 $P$ 是从 $T$ 上摘出来的,因此是一条简单路径,不经过同一个点两次,不经过同一条边两次。
设 $P$ 经过 $k$ 条边,$k +1$ 个点。形式化地,设 $P = p_0(=1) \xrightarrow{E_1}p_1 \xrightarrow{E_2}p_2\xrightarrow{E_3}\cdots\xrightarrow{E_k}p_k(=n)$。
设这 $k + 1$ 个点构成的点集为 $V_P = \{p_i\}$,这 $k$ 条边构成的边集为 $E_P = \{E_i\}$。
对于任意 $u \in V_P$,记 $u$ 在 $p$ 上的下标为 $\mathrm{id}(u)$。即,$p_{\mathrm{id}(u)} = u$。对于 $u \notin V_P$,$\mathrm{id}(u)$ 未定义。
设 $\mathrm{pre}(u)$ 表示 $T$ 上 $u$ 和 $n$ 的 LCA,并设 $\mathrm{prd}(u) = \mathrm{id(pre}(u))$。
$\mathrm{pre}(u)$ 一定是 $T$ 上 $n$ 的祖先,因此 $\mathrm{pre}(u)$ 一定在 $T(1, n) = P$ 上,即 $\mathrm{pre}(u) \in V_P$。这保证对所有 $u$,$\mathrm{prd}(u)$ 都是有定义的。
设 $G = (V, E)$ 的 **以 $\boldsymbol n$ 为根** 的,**满足从 $\boldsymbol 1$ 到 $\boldsymbol n$ 的路径和 $\boldsymbol P$ 相等的** 任意一棵最短路树 $R = (V, E_R)$。
**再次注意,我们必须保证 $\boldsymbol{R(1, n) = P = T(1, n)}$。**这样的 $R$ 一定存在,具体见后面算法流程的构造方式。
设 $D(u, n) = w(R(u, n))$。
设 $\mathrm{suf}(u)$ 表示 $R$ 上 $u$ 和 $1$ 的 LCA。并设 $\mathrm{sud}(u) = \mathrm{id(suf}(u))$。同理,$\mathrm{suf}(u) \in V_P$,所以对所有 $u$,$\mathrm{sud}(u)$ 都有定义。
设得有点多,放一张图直观理解一下。

上图中,只标了部分点的编号(黑色数字,红色数字)和边权(绿色数字),其余的省略。
上面这个图是一棵树,假设上面这个图是某个图 $G$ 的最短路树 $T$,那么:
- 最左面的点 $1$ 是 $T$ 的树根。
- $T(1, 3) = 1 \to 4 \to 6 \to 3$。
- $D(1, 3) = 1 + 4 + 2 = 7$。
- $P = T(1, n) = 1 \to 4 \to 5 \to 2 \to 7 \to n$,即橙色路径。$k = 5$,即 $P$ 的边数。
- $p_0 = 1$,$p_1 = 4$,$p_2 = 5$,$p_3 = 2$,$p_4 = 7$,$p_5 = n$。这些点构成点集 $V_P$,编号 $0 \sim k$。
- $E_1 = (1, 4)$,$E_2 = (4, 5)$,$E_3 = (5, 2)$,$E_4 = (2, 7)$,$E_5 = (7, n)$。这些边构成边集 $E_P$,编号 $1 \sim k$。
- $D = D(1, n) = 1 +3 + 1 + 5 + 2 = 12$。
- $\mathrm{id}(1) = 0$,$\mathrm{id}(4) = 1$,$\mathrm{id}(5) = 2$,$\mathrm{id}(2) = 3$,$\mathrm{id}(7) = 4$,$\mathrm{id}(n) = 5$。可以看做 $p$ 的逆运算。
- $\mathrm{pre}(3) = \mathrm{LCA}_T(3, n) = 4$,$\mathrm{prd}(3) = \mathrm{id(pre(3)) = id(4)} = 1$。
- $\mathrm{pre}(8) = \mathrm{LCA}_T(8, n) = 5$,$\mathrm{prd}(8) = \mathrm{id}(5) = 2$。
现在换个假设,如果上面这个图是某个图 $G$ 的最短路树 $R$,那么:
- 点 $n$ 是 $R$ 的树根。
- $R(3, n) = 3 \to 6 \to 4 \to 5 \to 2 \to 7 \to n$。
- $D(3, n) = 2 + 4 + 3 + 1 + 5 + 2 = 17$。
- $\mathrm{suf}(3) = \mathrm{LCA}_R(3, 1) = 4$,$\mathrm{sud}(3) = \mathrm{id}(\mathrm{suf}(3)) = \mathrm{id}(4) = 1$。
- $\mathrm{suf}(8) = \mathrm{LCA}_R(8, 1) = 5$,$\mathrm{sud}(8) = \mathrm{id}(5) = 2$。
### 显然的事实
读者应当认为以下事实的成立十分自然,这里只给出简要说明或不给出。
为方便理解,再次给出例图,设下面的树是 $T$。

- 对于任意 $0 \le i \le k$,$p_i \in V_P$。
- 对于任意 $u, v \in \boldsymbol{V_P}$,$T(u, v) = R(u, v) = P(u, v)$。
- 这条性质后面会用到,不要反应不过来。
- 对于任意 $u \in V$,$T(1, u) = P(1, \mathrm{pre}(u)) \oplus T(\mathrm{pre}(u), u)$。
- $T(1, u)$ 这条路径就是先按照主干 $P$ 走到 $u$ 和 $n$ 的 LCA $\mathrm{pre}(u)$ 处,然后再从 LCA 处沿着小分枝走到 $u$。
- 比如 $T(1, 3)$ 就是先按照 $P$ 走到 $4$,然后在按照小分枝走到 $3$。$T(1, 8)$ 是先按照 $P$ 走到 $5$,再按小分枝走到 $8$。
- 同理,对于任意 $u \in V$,$R(u, n) = R(u, \mathrm{suf}(u)) \oplus P(\mathrm{suf}(u), n)$。
- $R(u, n)$ 就是 $u$ 先按照小分枝走到 $u$ 和 $1$ 的 LCA $\mathrm{suf}(u)$ 处进入主干,然后再沿着主干到达 $n$。
- 对于任意 $u \in V$,$T(1, u)$ 这条路径放在 $G$ 上,是一条最短路径(根据最短路树的定义)。
- 对于任意 $u \in V$,$R(u, n)$ 这条路径放在 $G$ 上,是一条最短路径(同上)。
- 因此,$P$ 是一条 $1$ 到 $n$ 的最短路径。
- 一条最短路径 $X$ 的任意子路径 $X(u, v)$,是一条最短路径(否则 $X$ 可以把 $X(u, v)$ 这条子路径换成更短的从而让 $X$ 更短)。
- 如果一条 $u \rightsquigarrow v$ 的路径 $X$ 是一条从 $u$ 到 $v$ 的最短路径,那么把 $X$ 反过来走也是一条 $v$ 到 $u$ 的最短路径(仅在无向图上成立)。
- 对于从 $u$ 到 $v$ 的两条最短路径 $X$ 和 $Y$,有 $w(X) = w(Y)$。
- 因为 $G$ 是正权图,所以对于任何 $u, v \in V$,任何一条 $u$ 到 $v$ 的最短路径都是简单的(不经过同一点,同一边两次)。因为如果经过同一个点两次说明最短路径存在一个环,在正权图上明显不可能。而经过同一条边两次说明经过了其两个端点两次,同理不可能。
同时,这里给出两个 **错误** 结论:
【错误结论一】对于任意 $u$ 和 $v$,$T(u, v)$ 和 $R(u, v)$ 放在 $G$ 上是一条最短路径。
注意,最短路树只保证树上 **从根到任意节点的路径** 是原图上根到这个节点的最短路径。**任意两点间的路径则不保证。**
【错误结论二】对于最短路径 $X$,$Y$,$X$ 的终点等于 $Y$ 的起点,则 $X \oplus Y$ 的结果也是一条最短路径。
想象一个由三个点构成的环 $a$,$b$,$c$,其中 $w(a, b) = w(b, c) = w(a, c) = 1$。
这个例子里 $a \rightsquigarrow b$ 的最短路径是 $a \to b$,$b \rightsquigarrow c$ 的最短路径是 $b \to c$,但 $a \to b \to c$ 不是 $a \rightsquigarrow c$ 的最短路径($a \to c$ 才是)。
事实上,假设 $X$ 的终点和 $Y$ 的起点是 $x$,则上面 $X \oplus Y$ 的结果可以理解为必须经过点 $x$ 的最短路径。
### 引理
$\mathbf{Lemma\ 1}$ **对于任意 $\boldsymbol{e \not\in E_P}$,$\boldsymbol{\Delta(e) = D}$。**
删除 $e$ 不会影响最短路径 $P$,也不可能生成一条距离更小的路径,因此 $1$ 到 $n$ 的最短路仍然是 $D$。
这个引理告诉我们,只需关心 $e \in E_P$ 的 $\Delta(e)$ 即可。
$\mathbf{Lemma\ 2}$ **对于任意 $\boldsymbol {u \in V}$,$\boldsymbol{\mathbf{prd}(u) \le \mathbf{sud}(u)}$。**
反证法,假设 $\mathrm{prd}(u) > \mathrm{sud}(u)$,即在 $P$ 上,$\mathrm{pre}(u)$ 出现得比 $\mathrm{suf}(u)$ 晚。
此时 $T(1, \mathrm{pre}(u))$ 会经过 $\mathrm{suf}(u)$,而 $R(\mathrm{suf}(u), n)$ 会经过 $\mathrm{pre}(u)$。
于是 $T(1, u) = 1 \rightsquigarrow \mathrm{suf}(u) \rightsquigarrow \mathrm{pre}(u) \rightsquigarrow u$,$R(u, n) = u \rightsquigarrow \mathrm{suf}(u) \rightsquigarrow \mathrm{pre}(u) \rightsquigarrow n$。画个图吧。

其中,橙色路径就是 $P$,为 $T$ 和 $R$ 共有部分;绿色路径在 $T$ 上;红色路径在 $R$ 上。
上面的 $a$ 为绿色路径的权值,$b$ 为红色路径的权值,$c$ 为 $\mathrm{suf}(u)$ 和 $\mathrm{pre}(u)$ 中间橙色路径部分的权值。
> 当然,可能绿色路径上有部分边在 $R$ 上,红色路径上有部分边在 $T$ 上,但这不影响。
>
> 我们保证的是绿色路径上的所有边都在 $T$ 上,至于有没有在 $R$ 上的无所谓。同理红色路径上的所有边都在 $R$ 上。
因为 $T(\mathrm{pre}(u), u)$ 和 $T(\mathrm{suf}(u), u)$ 都是最短路径 $T(1, u)$ 的子路径,所以分别是最短路径。
因为无向图,所以 $T(u, \mathrm{pre}(u))$ 和 $T(u, \mathrm{suf}(u))$ 也分别是最短路径。这两条路径的权值分别对应图中的 $a$ 和 $a + c$。
同理因为 $R(u, \mathrm{suf}(u))$ 和 $R(u, \mathrm{pre}(u))$ 都是最短路径 $R(u, n)$ 的子路径,所以也分别是最短路径。
这两条路径的权值分别对应图中的 $b$ 和 $b + c$。
因为 $T(u, \mathrm{pre}(u))$ 和 $R(u, \mathrm{pre}(u))$ 是两条同起点同终点的最短路径,所以其权值相等,因此 $a = b + c$。
因为 $T(u, \mathrm{suf}(u))$ 和 $R(u, \mathrm{suf}(u))$ 是两条同起点同终点的最短路径,所以权值相等,因此 $b = a + c$。
这两个方程联立得到 $c = 0$。然而 $G$ 是正权图,$c$ 作为一条起点不等于终点的路径,权值不可能为 $0$。矛盾,假设不成立,命题得证。
注意上面的结论只适用于 **无向正权图。**
$\mathbf{Lemma\ 3.1}$ **在原图上(先不考虑删边),任意两点间的任意两条最短路径 $\boldsymbol X$ 和 $\boldsymbol Y$,满足 $\boldsymbol X$ 和 $\boldsymbol Y$ 的交点在 $\boldsymbol X$ 中与在 $\boldsymbol Y$ 中的出现顺序相同。**
其实这个推论跟结论没啥影响,但是我觉得还是个挺有用的推论,在此证明一下。
考虑否命题,即 $X$ 和 $Y$ 存在两个交点 $a$,$b$,满足 $X = 1 \rightsquigarrow a \rightsquigarrow b \rightsquigarrow n$,$Y = 1 \rightsquigarrow b \rightsquigarrow a \rightsquigarrow n$。我们试图说明这是假的。
考虑最短路径的子路径也是最短路径,并且两点间最短路相同,因此 $w(X(1, a)) = w(Y(1, a))$,$w(X(1, b)) = w(Y(1, b))$。
然后明显又有 $w(X(1, a)) + w(X(a, b)) = w(X(1, b))$,$w(Y(1, b)) + w(Y(b, a)) = w(Y(1, a))$。
联立得到 $w(X(a, b)) = -w(Y(b, a))$,又因为正权图上 $w(X(a, b)) > 0$,$w(Y(b, a)) > 0$,所以等式无法成立,反证法成功。
注意上面的结论只适用于 **正权图(有向,无向均可)。**
$\mathbf{Lemma\ 3.2}$ **对于 $\boldsymbol{e \in E_P}$,删除 $\boldsymbol e$ 后,$\boldsymbol 1$ 到 $\boldsymbol n$ 若可达,则任意一条 $\boldsymbol 1$ 到 $\boldsymbol n$ 的最短路径 $\boldsymbol Q$,满足 $\boldsymbol Q$ 和 $\boldsymbol P$ 的交点在 $\boldsymbol Q$ 中与在 $\boldsymbol P$ 中的出现顺序相同。即,如果 $\boldsymbol Q$ 先和 $\boldsymbol P$ 交于 $\boldsymbol{p_i}$,后交于 $\boldsymbol{p_j}$,则 $\boldsymbol{i < j}$。**
这应该还是个蛮重要的推论的,大多数题解省略了对此的证明,这里补充一下吧。
注意到 $Q$ 是删边最短路径,不一定是原图上的最短路径,所以不能直接移用 $\mathbf{Lemma\ 3.1}$ 的结论。
但证明思路差不多,还是考虑反证:假设 $P$ 和 $Q$ 存在两个交点 $a$,$b$,满足 $P = 1 \rightsquigarrow a \rightsquigarrow b \rightsquigarrow n$,$Q = 1 \rightsquigarrow b \rightsquigarrow a \rightsquigarrow n$。
因为删边后最短路不可能降低,所以 $w(Q(1, b)) \ge w(P(1, b))$,$w(Q(a, n)) \ge w(P(a, n))$。又因为路径权值全是正的,
所以 $w(Q(1, a)) = w(Q(1, b)) + w(Q(b, a)) > w(Q(1, b)) \ge w(P(1, b)) = w(P(1, a)) + w(P(a, b)) > w(P(1, a))$。
同理 $w(Q(b, n)) = w(Q(b, a)) + w(Q(a, n)) > w(Q(a, n)) \ge w(P(a, n)) = w(P(a, b)) + w(P(b, n)) > w(P(b, n))$。
分类讨论删去的边 $e$ 位置。
如果删去的边 $e$ 位于 $P(1, b)$ 上,即 $P(b, n)$ 还是通的,则删边后仍存在一条路径 $Q' = Q(1, b) \oplus P(b, n)$。考虑其权值 $w(Q') = w(Q(1, b)) + w(P(b, n)) < w(Q(1, b)) + w(Q(b, n)) = w(Q)$。存在一条比 $Q$ 更短的路径,与 $Q$ 是最短路径的假设矛盾。
如果删去的边 $e$ 位于 $P(b, n)$ 上,此时 $P(1, a)$ 连通。则删边后仍存在一条路径 $Q' = P(1, a) \oplus Q(a, n)$。考虑其权值 $w(Q') = w(P(1, a)) + w(Q(a, n)) < w(Q(1, a)) + w(Q(a, n)) = w(Q)$,同样和 $Q$ 是最短路径矛盾。
所以假设不成立,命题得证。
注意上面的结论只适用于 **正权图(有向,无向均可)。**
$\mathbf{Lemma\ 3.3}$ **对于 $\boldsymbol{e \in E_P}$,删除 $\boldsymbol e$ 后,$\boldsymbol 1$ 到 $\boldsymbol n$ 若可达,则存在一条 $\boldsymbol 1$ 到 $\boldsymbol n$ 的最短路径 $\boldsymbol Q$,满足 $\boldsymbol Q$ 从 $\boldsymbol 1$ 开始,先跟 $\boldsymbol P$ 共享一段前缀(可以只有 $\boldsymbol 1$ 一个点),然后腾空一段绕过 $\boldsymbol e$(期间与 $\boldsymbol P$ 无任何交点),最后和 $\boldsymbol P$ 共享一段后缀(可以只有 $\boldsymbol n$ 一个点)到达 $\boldsymbol n$。**
可采取的证法很多,这里采用一种最直观的一种。
我们将 $P$ 这条 $1 \rightsquigarrow n$ 的路径从左到右排列成一条直线(为方便后面描述),即对于 $0 \le i < j \le k$,我们认为 $p_i$ 出现在 $p_j$ 的左侧。
根据 $\mathbf{Lemma\ 3.2}$ 的结论,任何一条 $1$ 到 $n$ 的最短路径 $Q'$ 和 $P$ 一定先相交在位于左侧的点,再相交在位于右侧的点。也即,不会出现 $Q'$ 先和 $P$ 交在右面一个点,然后又回去交在左面一个点的情况。
因此,所有 $Q'$ 都是从 $1$ 开始,反复地按照 $P$ 走一段,然后再离开一段,然后再回到 $P$ 走一段,再离开一段……往复进行,最后到达 $n$。并且和 $P$ 的交点一定越来越靠右。
据此:我们画出一个 $Q'$ 的示意图:
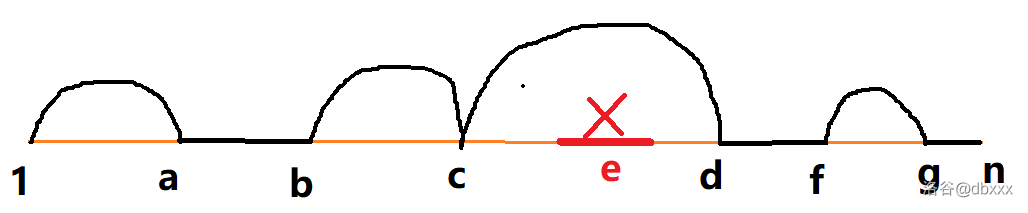
不难发现上面这个例子中,$Q'(1, a)$ 可以替换成 $P(1, a)$,$Q'(b, c)$ 可以替换成 $P(b, c)$,$Q'(f, g)$ 可以替换成 $P(f, g)$。
只有 $Q'(c, d)$ 这一段飞起来的弧会越过删除的边 $e$,$P(c, d)$ 不再连通,所以我们应该保留这段弧。
类似地,所有 $Q'$ 中飞起来的弧里,只会有一个越过边 $e$,我们保留这段弧,并将其他所有弧替换成 $P$ 上的子路径。
就可以构造一个从 $1$ 出发,先按照 $P$ 走,然后只腾空一段绕过 $e$,然后再按照 $P$ 走到 $n$ 的路径了。
注意上面的结论只适用于 **正权图(有向,无向均可)。**
$\mathbf{Lemma\ 4}$ **对于 $\boldsymbol{e \in E_P}$,删除 $\boldsymbol{e = E_t = (p_{t - 1}, p_t)}$ 后,$\boldsymbol 1$ 到 $\boldsymbol n$ 若可达,则存在一条 $\boldsymbol 1$ 到 $\boldsymbol n$ 的最短路径 $\boldsymbol Q$ 和两个点 $\boldsymbol a$,$\boldsymbol b$,满足 $\boldsymbol{(a, b) \in E \setminus E_P}$ 且 $\boldsymbol{Q = T(1, a) \oplus (a \to b) \oplus R(b, n)}$ 且 $\boldsymbol{\mathbf{prd}(a) \le t - 1}$ 且 $\boldsymbol{\mathbf{sud}(b) \ge t}$。**
先根据 $\mathbf {Lemma\ 3.3}$ 构造出 $1$ 到 $n$ 的一条删 $e$ 最短路径 $Q'$。它和 $P$ 共享前缀和后缀,中间腾空而起绕过 $e$。
设 $Q'$ 和 $P$ 共享的前缀是 $P(1, p_x)$,共享的后缀是 $P(p_y, n)$,中间腾空而起的部分即 $Q'(p_x, p_y)$。
因为 $T(p_x, p_y) = P(p_x, p_y)$,明显地 $Q'(p_x, p_y) \ne P(p_x, p_y)$,所以 $Q'(p_x, p_y) \ne T(p_x, p_y)$,即 $Q'(p_x, p_y)$ 一定出现了一条不在 $T$ 上的边。
然后又有 $Q'(1, p_x) = P(1, p_x)$,$Q'(p_y, n) = P(p_y, n)$ 上所有边都在 $T$ 上。
综上,$Q'$ 上一定存在不在 $T$ 上的边,且这些边一定都在 $Q'(p_x, p_y)$ 上,也就是中间那段腾空而起的弧上。
考虑 $Q'$ 上 **最后一条**(即最接近 $n$ 的)不在 $T$ 上的边 $(c, d)$,并设 $c$ 是那个更接近 $1$ 的端点,$d$ 是那个更接近 $n$ 的端点。
根据题设,$Q'(d, n)$ 全程在 $T$ 上,即 $Q'(d, n) = T(d, n)$。
考虑 $T(d, n) = T(d, \mathrm{pre}(d)) \oplus P(\mathrm{pre}(d), n)$,为保证 $P(\mathrm{pre}(d), n)$ 是通路,我们必须让 $\mathrm{prd}(d) \ge t$。
综上,$Q'$ 上一定至少存在一条不在 $T$ 上的边 $(a, b)$,满足 $\mathrm{prd}(d) \ge t$。
考虑 $Q'$ 上 **第一条**(即最接近 $1$ 的)不在 $T$ 上,并且满足 $\mathrm{prd}(b) \ge t$ 的边 $(a, b)$。设 $a$ 是更接近 $1$ 的那个端点,$b$ 是更接近 $n$ 的那个端点。
根据 $\mathbf{Lemma\ 2}$,$\mathrm{sud}(b) \ge \mathrm{prd}(b)$,所以 $\mathrm{sud}(b) \ge t$,因此 $\mathrm{suf}(b)$ 在 $e$ 的右侧。所以,$R(b, n)$ 在删 $e$ 后仍连通。
所以考虑将 $Q'$ 中的 $Q'(b, n)$ 替换成 $R(b, n)$,设新路径为 $Q''$。不难发现,$Q''$ 仍然是一条合法的删边最短路径。
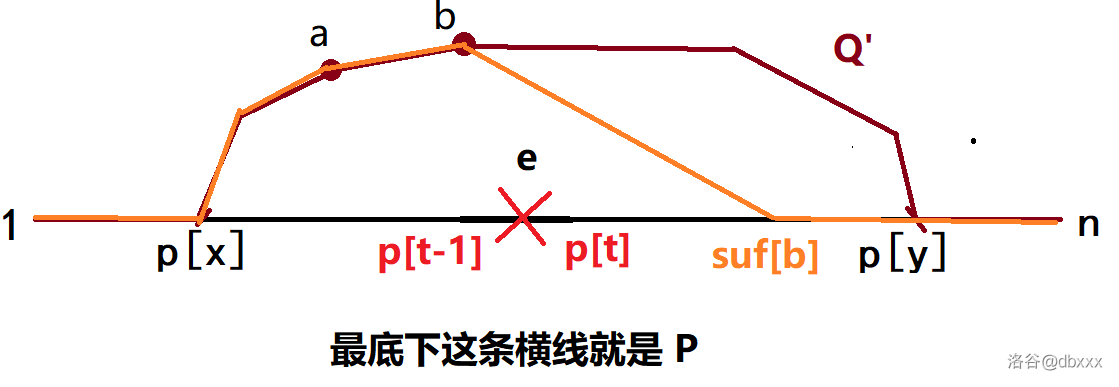
上面那条橙色的路径就是 $Q''$。
此时分类讨论:
**【情况一】** 如果 $Q''(1, a)$ 上所有边都在 $T$ 上。
$Q''(1, a) = T(1, a)$,因为 $Q''$ 是合法删边最短路径,所以 $T(1, a)$ 一定是通的。所以 $\mathrm{prd}(a) \le t - 1$。
因为 $(a, b)$ 不在 $T$ 上,那就更不可能在 $P$ 上。所以:
- $(a, b) \in E \setminus E_P$。
- $Q''$ 是一条合法删边 $1$ 到 $n$ 最短路径。
- $Q'' = T(1, a) \oplus (a \to b) \oplus R(b, n)$。
- $\mathrm{prd}(a) \le t - 1$。
- $\mathrm{sud}(b) \ge t$。
命题成立。
**【情况二】** 如果 $Q''(1, a)$ 上存在一条不在 $T$ 上的边。
设 $Q''(1, a)$ 上 **最后一条** 不在 $T$ 上的边为 $(f, g)$。设 $f$ 接近 $1$,$g$ 接近 $n$。
根据:
- $(a, b)$ 是 **第一条** 不在 $T$ 上,并且满足 $\mathrm{prd}(b) \ge t$ 的边。
- $(f, g)$ 不在 $T$ 上。
- $(f, g)$ 在 $Q''$ 上出现的比 $(a, b)$ 早。
可以推出 $\mathrm{prd}(g) < t$,或者说,$\mathrm{prd}(g) \le t - 1$。
于是此时 $\mathrm{prd}(g)$ 出现在 $e$ 的左侧,即删 $e$ 后 $P(1, g)$ 仍然连通。考虑将 $Q''$ 中的 $Q''(1, g)$ 替换成 $T(1, g)$,设为 $Q$。
不难发现 $Q$ 仍是一条合法删边 $1$ 到 $n$ 最短路径。
又根据 $(f, g)$ 的选取条件可知,$Q''(g, a) = Q(g, a)$ 这段子路径上的所有边都在 $T$ 上。
那么此时,$Q(1, g)$ 都在 $T$ 上,$Q(g, a)$ 都在 $T$ 上,$Q(b, n)$ 都在 $R$ 上。
所以 $Q = T(1, a) \oplus (a \to b) \oplus R(b, n)$。
$Q(1, a) = T(1, a)$,所以 $T(1, a)$ 连通,所以 $\mathrm{prd}(a) \le t - 1$。又有 $(a, b)$ 不在 $T$ 上,所以 $(a, b)$ 不在 $P$ 上,此时:
- $(a, b) \in E \setminus E_P$。
- $Q$ 是一条合法删边 $1$ 到 $n$ 最短路径。
- $Q = T(1, a) \oplus (a \to b) \oplus R(b, n)$。
- $\mathrm{prd}(a) \le t - 1$。
- $\mathrm{sud}(b) \ge t$。
命题成立。
上面的证明用到了只适用于无向正权图的 $\mathbf{Lemma\ 2}$,因此该推论只适用于 **无向正权图。**
$\mathbf{Lemma\ 5}$ **设 $\boldsymbol{S(i) = \{D(1, a) + w(a, b) + D(b, n) \mathop | (a, b) \in E \setminus E_P ,\mathbf{prd}(a) \le i - 1, \mathbf{sud}(b) \ge i\}}$。则当 $\boldsymbol{S(i) \ne \mathbf\varnothing}$ 时,$\boldsymbol{\Delta(E_i) = \min(S(i))}$;否则,$\boldsymbol{\Delta(E_i) = +\infty}$,即此时 $\boldsymbol{1 \rightsquigarrow n}$ 不可达。**
注:假设 $E \setminus E_P$ 有一条连接点 $2$ 和点 $3$ 的边,那么 $a = 2, b = 3$ 和 $a = 3, b = 2$ 这两种情况都满足 $(a, b) \in E \setminus E_P$,都需要代入到 $S(i)$ 中。即如果 $\mathrm{prd}(2) \le i - 1$ 且 $\mathrm{sud}(3) \ge i$,那么 $S(i)$ 中会有元素 $D(1, 2) + w(2, 3) + D(3, n)$;如果 $\mathrm{prd}(3) \le i - 1$ 且 $\mathrm{sud}(2) \ge i$,那么 $S(i)$ 中会有一个元素 $D(1, 3) + w(3, 2) + D(2, n)$。
上面这两个“如果”并不是对立关系,可以同时满足,也可以同时不满足,当然也可以满足一个而不满足另一个。
也就是对于每一条边,我们考虑它的两个端点时,要按照两种不同的顺序试两次代入 $S$。
---
我们设 $W(a, b) = D(1, a) + w(a, b) + D(b, n)$,即 $T(1, a) \oplus (a \to b) \oplus R(b, n)$ 这条路径的权值。
重新观察一下 $\mathbf{Lemma\ 4}$:
> $\mathbf{Lemma\ 4}$ 对于 ${e \in E_P}$,删除 ${e = E_t = (p_{t - 1}, p_t)}$ 后,$ 1$ 到 $ n$ 若可达,则存在一条 $ 1$ 到 $ n$ 的最短路径 $ Q$ 和两个点 $a$,$b$,满足 ${(a, b) \in E \setminus E_P}$ 且 ${Q = T(1, a) \oplus (a \to b) \oplus R(b, n)}$ 且 ${\mathrm{prd}(a) \le t - 1}$ 且 ${\mathrm{sud}(b) \ge t }$。
不难发现,它等价于:
对于 $e \in E_P$,删除 $e = E_t = (p_{t - 1}, p_t)$ 后,$1$ 到 $n$ 若可达,则存在两个点 $a$,$b$,满足 $(a, b) \in E \setminus E_P$ 且 $\Delta(E_t) = W(a, b)$ 且 $\mathrm{prd}(a) \le t - 1$ 且 $\mathrm{sud}(b) \ge t$。
令 $S(t) = \{W(a, b) \mathop | (a, b) \in E \setminus E_P, \mathrm{prd}(a) \le t - 1, \mathrm{sud}(b) \ge t\}$,则上面的这条又等价于:
如果删除 $E_t$ 后 $1$ 到 $n$ 可达,就一定有 $\Delta(E_t) \in S(t)$。
考虑 $S(t)$ 中任何一个元素,由于 $\mathrm{prd}(a) \le t - 1$ 和 $\mathrm{sud}(b) \ge t$ 的存在,所以 $T(1, a) + w(a, b) + R(b, n)$ 至少是一条删了 $E_t$ 之后仍然通的合法路径(只是不保证最短)。所以 $S(t)$ 中所有元素都 $\ge \Delta(E_t)$,即 $\Delta(E_t) \le \min(S(t))$。
而如果 $\Delta(E_t) < \min(S(t))$,就不满足 $\Delta(E_t) \in S(t)$ 了,所以 $\Delta(E_t) = \min(S(t))$。
---
而 $\mathbf{Lemma\ 4}$ 的逆否命题也是真命题,等价于:
如果不存在两个点 $a$,$b$,满足 $(a, b) \in E \setminus E_P$ 且 $\Delta(E_t) = W(a, b)$ 且 $\mathrm{prd}(a) \le t - 1$ 且 $\mathrm{sud}(b) \ge t$,则删除 $E_t$ 后一定不可达。
又不难发现,它等价于:
如果 $S(t) = \varnothing$,则 $\Delta(E_i) = +\infty$。
而如果 $S(t) \ne \varnothing$,由于 $S(t)$ 中的任意一个元素都可以对应一种 $1$ 到 $n$ 的通路,能推得 $1$ 到 $n$ 可达,进而推得 $\Delta(E_t) = \min(S(t))$,证毕。
$\mathbf{Lemma\ 5}$ 由只适用于无向正权图的 $\mathbf{Lemma\ 4}$ 推得,因此该推论只适用于 **无向正权图。**
### 算法流程
#### 准备工作
首先,在原图上以源点 $1$ 跑 dijkstra,得到以 $1$ 为根的最短路树 $T$,$P$,$D$,$D(1, u)$。
然后考虑根据 $T$ 求出 $\mathrm{pre}(u)$。当然可以倍增 LCA,但是由于我们要批量求解 $\mathrm{LCA}(u, n)$,$n$ 是定点。
所以我们可以考虑另一种更方便的做法:将 $T$ 上 $1 \rightsquigarrow n$ 这条链,即 $P$ 上的边全部断掉。
这样会形成森林(可能有孤立点),而且每棵树应恰有一个点属于 $V_P$,设这个点为这棵树的根。
于是对于每个点 $u$,$\mathrm{pre}(u) = \mathrm{LCA}(u, n)$ 就是 $u$ 所在的树根。
还是以这个图为例:

我们断掉 $P$ 上的边,得到:
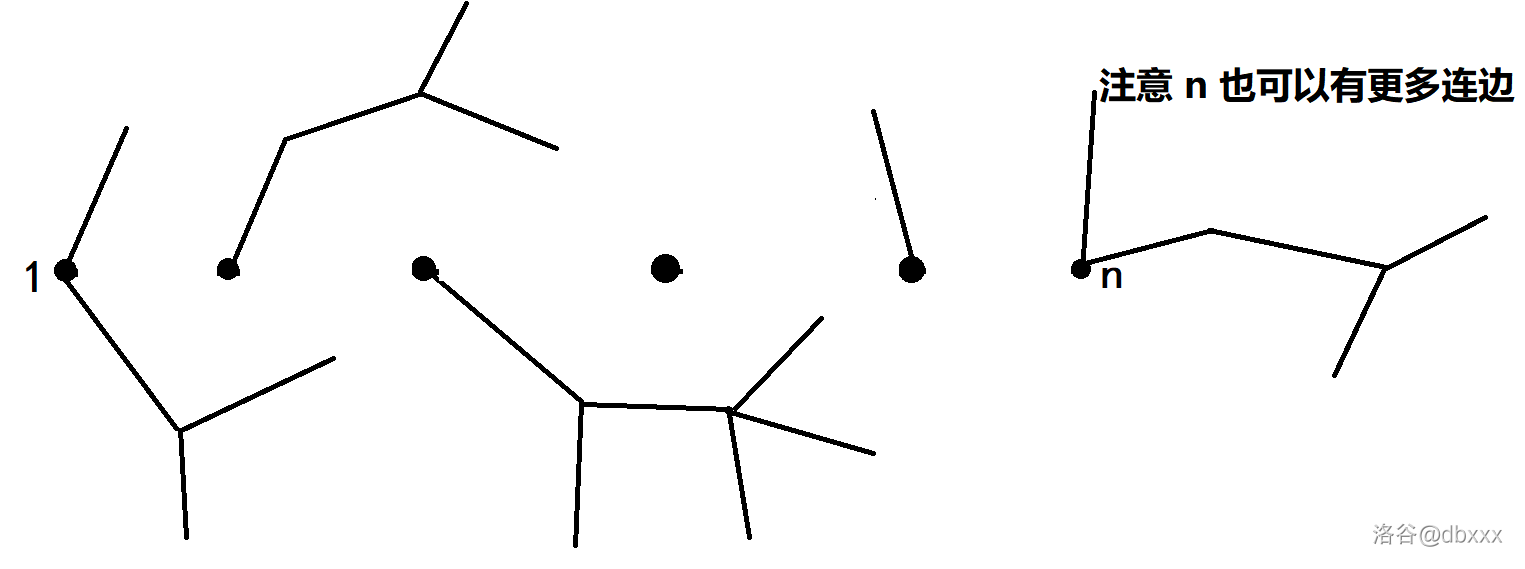
实心黑点对应 $V_P$ 上的某个点,设其为所在树的根。不难发现,对于每个点 $u$,$\mathrm{pre}(u) = \mathrm{LCA}(u, n)$ 就是 $u$ 所在的树根。
不过由于后面要用到的是 $\mathrm{prd}$,所以可以直接求 $\mathrm{prd}$,即树根的 $\mathrm{id}$。具体看下面例题代码。
另外注意,可以有点的 $\mathrm{prd}$ 是 $0$,也即 $\mathrm{pre}$ 为 $p_0 = 1$ 的点。
然后考虑构建以 $n$ 为根的最短路树 $R$。别忘了,我们要保证 $R(1, n) = P = T(1, n)$。
其实只需要 dijkstra 构建 $R$ 之前,先把 $R(1, n)$ 这条链直接链接成 $P$,并且把 $P = R(1, n)$ 上的所有点 $u$ 的 `disn[u]`(dijkstra 里用到的,$u$ 和 $n$ 的距离数组)全都先预处理好(直接设置为 $w(P(u, n))$)。
然后再 dijkstra 构建 $R$ 即可,`disn[v] < disn[u] + w` 的时候再把 `fa[v]`($v$ 在 $R$ 上的父亲)切换成 $u$,就能保证刚强制连接的 $R(1, n)$ 不会被修改。这里具体可以读代码。
$\mathrm{sud}$ 的求解和 $\mathrm{prd}$ 同理。
#### 维护与计算
根据强大的 $\mathrm{Lemma\ 1}$,对于任何 $e \not\in E_P$,$\Delta(e) = D$。
根据强大的 $\mathrm{Lemma\ 5}$,对于任何 $e \in E_P$,设 $e = E_i$,有:
$$
\Delta(E_i) = \min(S(i)) = \min\{W(a, b) \mathop | (a, b) \in E \setminus E_P,\mathrm{prd}(a) \le i - 1, \mathrm{sud}(b) \ge i\}
$$
然而直接求解,时间复杂度太高了。
对 $\mathrm{prd}(a) \le i - 1, \mathrm{sud}(b) \ge i$ 变形得 $\mathrm{prd}(a) + 1 \le i \le \mathrm{sud}(b)$。
于是我们有以下策略。
- 初始时创建若干空可重集合 $S'(1),\ldots,S'(k)$。
- 枚举非 $E_P$ 边 $(a, b)$,如果 $\mathrm{prd}(a) + 1 \le \mathrm{sud}(b)$,将 $W(a, b)$ 分别插入 $S'(\mathrm{prd}(a) + 1), S'(\mathrm{prd}(a) + 2),\ldots,S'(\mathrm{sud}(b))$。
- 注意上面,每一条连接 $a$ 和 $b$ 的边要按照 $(a, b)$ 和 $(b, a)$ 枚举两次。
- 待枚举结束后,$S'(i) = S(i)$。
这个算法仍然不现实,但注意到,我们并不在意 $S'$ 或 $S$ 集合的具体内容,只关心这些集合的最小值。
因此稍作改动便可形成如下算法:
- 初始定义 $\mathrm{ans}(i) = +\infty$。
- 对于每条非 $E_P$ 边 $(a, b)$,对下标在 $[\mathrm{prd}(a) +1, \mathrm{sud}(b)]$ 范围内的 $\mathrm{ans}$ 与 $W(a, b)$ 区间取 $\min$。
- 对于 $\mathrm{prd}(a) + 1 > \mathrm{sud}(b)$ 这种情况,直接认为上面那个区间是空的,也就是对 $\mathrm{ans}$ 没有影响。
- 同样注意每一条连接 $a$ 和 $b$ 的边要按照 $(a, b)$ 和 $(b, a)$ 枚举两次。
- 最后 $\mathrm{ans}(i) = \Delta(E_i)$。如果某个 $\mathrm{ans}(i)$ 仍然是 $+\infty$,证明断掉 $E_i$ 后 $1 \rightsquigarrow n$ 不可达。
到这里思路就很明朗了。可以线段树!先进行所有区间取 $\min$,然后回答时对 $\mathrm{ans}(i)$ 单点在线查询。
不过,因为询问都在区间操作之后,也可以先预处理出所有 $\mathrm{ans}(i)$,最后 $\Theta(1)$ 回答 $\Delta(e)$ 的询问。
所以可以离线 multiset 扫描线。
具体来说,$i$ 从 $1 \rightsquigarrow k$ 求解 $\mathrm{ans}(i)$,维护 multiset 上的最小值。
枚举到一个新的 $i$ 时:
- 对 multiset 插入影响区间左端点 $\mathrm{prd}(a) + 1$ 等于 $i$ 的 $W(a, b)$。
- 如果此时 multiset 为空,则 $\mathrm{ans}(i) = +\infty$;否则,$\mathrm{ans}(i)$ 应该为 multiset 的最小值。
- 最后在 multiset 中删除影响区间右端点 $\mathrm{sud}(b)$ 等于 $i$ 的 $W(a, b)$。
删边最短路就做完了。
### 时间复杂度
$\Theta((m + n)\log m + q)$。
其实删边最短路的原理是,通过一种非常巧妙的办法,将原问题转化成了一个可以用线段树解决的问题。
### 例题
#### bzoj 2725 [Violet 6]故乡的梦
[bzoj 2725](https://darkbzoj.cc/problem/2725)。模板题。
下面的 $s$ 和 $t$ 指的是原题上的源点 $S$ 和终点 $T$。
事实上刚刚讲的是 $s = 1$,$t = n$ 的情况。但是显然,源点终点编号不会影响做法。
不过,不保证图联通,也不保证初始时 $s$ 和 $t$ 在同一个连通块,我们就需要考虑一些小细节处理了:
- 如果 $s$ 和 $t$ 不连通,求出的最短路为 $+\infty$,此时特判所有询问都输出 `Infinity`。
- $s$ 和 $t$ 连通,但图不联通?
- 不在 $s$ 和 $t$ 所在连通块上的边 $e$ 可以正确地被判断不属于 $E_P$,得到 $\Delta(e) = D$。
- 判断不在 $s$ 和 $t$ 所在连通块上的点 $u$,可以用求解出的 $1 \rightsquigarrow u$ 的最短路是否有穷判断。
- 我们令不在 $s$ 和 $t$ 所在连通块上的点 $u$,有 $\mathrm{prd}(u) = \mathrm{sud}(u) = -1$。
- 这样以来,不在 $s$ 和 $t$ 所在连通块上的边 $e$ 的影响区间是 $[0, -1]$,也就是空区间,不会影响 $\Delta(E_i)$,这正是我们期望的。
问题就解决了。
```cpp
/*
* @Author: crab-in-the-northeast
* @Date: 2023-04-07 16:01:16
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2023-04-07 19:34:12
*/
#include <bits/stdc++.h>
#define int long long
inline int read() {
int x = 0;
bool f = true;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-')
f = false;
for (; isdigit(ch); ch = getchar())
x = (x << 1) + (x << 3) + ch - '0';
return f ? x : (~(x - 1));
}
const int maxn = (int)2e5 + 5;
const int maxm = (int)2e5 + 5;
typedef std :: pair <int, int> pii;
std :: vector <pii> G[maxn];
// G[u] 存储一个顶点是 u 的边信息
// pii 第一项为边连接的另一个顶点 v,第二项为边编号
int wei[maxm]; // 记录边编号为 i 的边权
std :: unordered_map <int, int> eid;
// 这个用来根据边两边的点信息还原出边的编号
// 因为 umap 自带哈希函数不支持 pair
// 考虑给键值传个 u * n + v
namespace T {
int fa[maxn], pred[maxn], dis[maxn];
// 分别代表:
// T 上 u 的父亲;
// T 上连接 u 和 fa[u] 的边(称之为前驱边)编号;
// D(1, u) = w(T(1, u)) 的值,也是原图上 1 到 u 的最短路
}
namespace R {
int fa[maxn], pred[maxn], dis[maxn];
// 分别代表:
// R 上 u 的父亲;
// R 上连接 u 和 fa[u] 的边(称之为前驱边)编号;
// D(u, n) = w(R(u, n)) 的值,也是原图上 u 到 n 的最短路
}
int prd[maxn], sud[maxn];
int tag[maxm];
// tag[i] 记录 i 编号这条边在 E 上的下标,如果不在 E_P 上则为 0
int ans[maxn];
// ans[i] 记录删除 E_i 的最短路,这里开 maxn 是因为最短路边数不会超过 n - 1
std :: vector <int> ls[maxn];
std :: vector <int> rs[maxn];
// ls[i] 存放左端点在 i 的区间修改信息,rs[i] 存放右端点在 i 的区间修改信息
int s, t, n, k; // k 表示最短路 P 的边数
inline int getprd(int u) {
return prd[u] = (prd[u] != -1 ? prd[u] : getprd(T :: fa[u]));
}
inline int getsud(int u) {
return sud[u] = (sud[u] != -1 ? sud[u] : getsud(R :: fa[u]));
}
inline bool init() {
std :: memset(T :: dis, 0x3f, sizeof(T :: dis));
const int inf = T :: dis[0];
T :: dis[s] = 0;
std :: priority_queue <pii> q;
q.push({0, s});
while (!q.empty()) {
int d = q.top().first, u = q.top().second;
q.pop();
if (d + T :: dis[u])
continue;
for (pii e : G[u]) {
int v = e.first, id = e.second, w = wei[id];
if (T :: dis[u] + w < T :: dis[v]) {
T :: dis[v] = T :: dis[u] + w;
T :: fa[v] = u;
T :: pred[v] = id;
q.push({-T :: dis[v], v});
}
}
}
if (T :: dis[t] >= inf)
return false;
std :: vector <int> P; // 这个 P 实际是 V_P
for (int u = t; u; u = T :: fa[u])
P.push_back(u);
std :: reverse(P.begin(), P.end());
k = (int)P.size() - 1;
// 在 P 上,点编号 0~k,共 k+1 个;边编号 1~k,共 k 个。
std :: memset(prd, -1, sizeof(prd));
std :: memset(sud, -1, sizeof(sud));
std :: memset(R :: dis, 0x3f, sizeof(R :: dis));
for (int i = 0; i <= k; ++i) {
prd[P[i]] = i; // 设置 P 上点的 prd
sud[P[i]] = i; // 设置 P 上点的 sud
if (i >= 1)
// 对于 i >= 1, P[i] 在 T 上的前驱边就是 E[i]
tag[T :: pred[P[i]]] = i; // tag[i] 记录 i 编号这条边在 E 上的下标,如果不在 E_P 上则为 0
R :: dis[P[i]] = T :: dis[t] - T :: dis[P[i]];
// P[i] 到 t 的距离等于 s 到 t 的距离 - s 到 P[i] 的距离
q.push({-R :: dis[P[i]], P[i]}); // 这些点的最短路确定,已经可以推入 dij 的优先队列了
// 有个负号是因为本人 dij 的写法
if (i < k) { // 这里是强制连边部分
R :: fa[P[i]] = P[i + 1]; // 把 P[i] 在 R 上的父亲设为 P[i + 1]
R :: pred[P[i]] = T :: pred[P[i + 1]]; // 把 P[i] 在 R 上的前驱边设为 P[i + 1] 在 T 上的前驱边
}
}
while (!q.empty()) {
int d = q.top().first, u = q.top().second;
q.pop();
if (d + R :: dis[u])
continue;
for (pii e : G[u]) {
int v = e.first, id = e.second, w = wei[id];
if (R :: dis[u] + w < R :: dis[v]) {
R :: dis[v] = R :: dis[u] + w;
R :: fa[v] = u;
R :: pred[v] = id;
q.push({-R :: dis[v], v});
}
}
}
for (int u = 1; u <= n; ++u) {
if (T :: dis[u] < inf) {
getprd(u);
getsud(u); // 处理好所有点的 prd 和 sud
}
}
return true;
}
signed main() {
n = read();
int m = read();
for (int i = 1; i <= m; ++i) {
int u = read(), v = read(), w = read();
G[u].push_back({v, i});
G[v].push_back({u, i});
wei[i] = w;
if (u > v)
std :: swap(u, v);
eid[u * n + v] = i;
}
s = read(), t = read();
if (!init()) {
int q = read();
while (q--)
puts("Infinity");
}
for (int u = 1; u <= n; ++u) {
for (pii e : G[u]) {
// 这种枚举方式下,一条边 (u, v) 会被作为 (u, v) 和 (v, u) 两次被枚举到,正是我们所期望的
int v = e.first, id = e.second, w = wei[id];
if (tag[id])
continue;
if (prd[u] < sud[v]) {
int W = T :: dis[u] + w + R :: dis[v];
ls[prd[u] + 1].push_back(W);
rs[sud[v]].push_back(W);
}
}
}
std :: multiset <int> S;
std :: memset(ans, 0x3f, sizeof(ans));
const int inf = ans[0];
for (int i = 1; i <= k; ++i) {
for (int d : ls[i])
S.insert(d);
if (!S.empty())
ans[i] = *S.begin();
for (int d : rs[i])
S.erase(S.find(d));
}
int q = read();
while (q--) {
int u = read(), v = read();
if (u > v)
std :: swap(u, v);
int id = eid[u * n + v];
if (tag[id]) {
int W = ans[tag[id]];
if (W == inf)
puts("Infinity");
else
printf("%lld\n", W);
} else
printf("%lld\n", T :: dis[t]);
}
return 0;
}
```
#### CF1163F Indecisive Taxi Fee
与删边最短路不同,这次是改边最短路。
还是先生成 $T$ 和最短路径 $P$,并计算最短路 $D$。假设待修改边是 $e$,修改前的边权是 $w(e)$,修改后的边权是 $x$。
明显地,无论怎么改,新图上的最短路就是两种最短路的 $\min$:必经 $e$ 的最短路,以及不经过 $e$ 的最短路。
**【如果 $\boldsymbol{e \notin E_P}$】**
这种情况是不经过 $e$ 的最短路更简单:就是 $D$。
必经 $e$ 的最短路其实也挺简单。假设 $e = (u, v)$,那么经过 $e$ 有两种方式:从 $u$ 进入,从 $v$ 离开;或者从 $v$ 进入,从 $u$ 离开。
因此必经 $e$ 的最短路是 $\min(D(1, u) + x + D(v, n), D(1, v) + x + D(u, n))$。
那么这种情况的总最短路就是 $\min(D, D(1, u) + x + D(v, n), D(1, v) + x + D(u, n))$。
必经最短路在 OI 中还是挺常出现的,值得注意。
**【如果 $\boldsymbol{e \in E_P}$】**
这种情况是经过 $e$ 的最短路更简单:就是 $D - w(e) + x$(注意 $e$ 的边权有修改)。
那不经过 $e$ 的最短路是什么?删边最短路!于是问题解决。
同样地注意,本题只保证 $1$ 和 $n$ 联通,不保证整个图联通。
```cpp
/*
* @Author: crab-in-the-northeast
* @Date: 2023-04-07 19:01:35
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2023-04-07 22:22:22
*/
#include <bits/stdc++.h>
#define int long long
inline int read() {
int x = 0;
bool f = true;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-')
f = false;
for (; isdigit(ch); ch = getchar())
x = (x << 1) + (x << 3) + ch - '0';
return f ? x : (~(x - 1));
}
const int maxn = (int)2e5 + 5;
const int maxm = (int)2e5 + 5;
typedef std :: pair <int, int> pii;
std :: vector <pii> G[maxn];
int wei[maxm], us[maxm], vs[maxm];
std :: vector <int> ls[maxn], rs[maxn];
int n, k;
namespace T {
int fa[maxn], pred[maxn], dis[maxn];
}
namespace R {
int fa[maxn], pred[maxn], dis[maxn];
}
int prd[maxn], sud[maxn], ans[maxn];
int tag[maxm];
inline int getprd(int u) {
return prd[u] = (prd[u] != -1 ? prd[u] : getprd(T :: fa[u]));
}
inline int getsud(int u) {
return sud[u] = (sud[u] != -1 ? sud[u] : getsud(R :: fa[u]));
}
inline void init() {
std :: memset(T :: dis, 0x3f, sizeof(T :: dis));
const int inf = T :: dis[0];
T :: dis[1] = 0;
std :: priority_queue <pii> q;
q.push({0, 1});
while (!q.empty()) {
int d = q.top().first, u = q.top().second;
q.pop();
if (d + T :: dis[u])
continue;
for (pii e : G[u]) {
int v = e.first, id = e.second, w = wei[id];
if (T :: dis[u] + w < T :: dis[v]) {
T :: dis[v] = T :: dis[u] + w;
T :: fa[v] = u;
T :: pred[v] = id;
q.push({-T :: dis[v], v});
}
}
}
std :: vector <int> P;
for (int u = n; u; u = T :: fa[u])
P.push_back(u);
std :: reverse(P.begin(), P.end());
k = (int)P.size() - 1;
std :: memset(prd, -1, sizeof(prd));
std :: memset(sud, -1, sizeof(sud));
std :: memset(R :: dis, 0x3f, sizeof(R :: dis));
for (int i = 0; i <= k; ++i) {
prd[P[i]] = i;
sud[P[i]] = i;
if (i >= 1)
tag[T :: pred[P[i]]] = i;
R :: dis[P[i]] = T :: dis[n] - T :: dis[P[i]];
q.push({-R :: dis[P[i]], P[i]});
if (i < k) {
R :: fa[P[i]] = P[i + 1];
R :: pred[P[i]] = T :: pred[P[i + 1]];
}
}
while (!q.empty()) {
int d = q.top().first, u = q.top().second;
q.pop();
if (d + R :: dis[u])
continue;
for (pii e : G[u]) {
int v = e.first, id = e.second, w = wei[id];
if (R :: dis[u] + w < R :: dis[v]) {
R :: dis[v] = R :: dis[u] + w;
R :: fa[v] = u;
R :: pred[v] = id;
q.push({-R :: dis[v], v});
}
}
}
for (int u = 1; u <= n; ++u) {
if (T :: dis[u] < inf) {
getprd(u);
getsud(u);
}
}
}
signed main() {
n = read();
int m = read(), q = read();
for (int i = 1; i <= m; ++i) {
int u = us[i] = read(), v = vs[i] = read(), w = read();
G[u].push_back({v, i});
G[v].push_back({u, i});
wei[i] = w;
}
init();
for (int u = 1; u <= n; ++u) {
for (pii e : G[u]) {
int v = e.first, id = e.second, w = wei[id];
if (!tag[id] && prd[u] < sud[v]) {
int W = T :: dis[u] + w + R :: dis[v];
ls[prd[u] + 1].push_back(W);
rs[sud[v]].push_back(W);
}
}
}
std :: multiset <int> S;
std :: memset(ans, 0x3f, sizeof(ans));
for (int i = 1; i <= k; ++i) {
for (int d : ls[i])
S.insert(d);
if (!S.empty())
ans[i] = *S.begin();
for (int d : rs[i])
S.erase(S.find(d));
}
while (q--) {
int t = read(), x = read(), u = us[t], v = vs[t], w = wei[t];
printf("%lld\n", tag[t] ?
std :: min(ans[tag[t]], T :: dis[n] - w + x) :
std :: min({T :: dis[n], T :: dis[u] + x + R :: dis[v], T :: dis[v] + x + R :: dis[u]}));
}
return 0;
}
```
## 有向图(疑似无靠谱做法)
由于无向图的 $\mathbf{Lemma\ 5}$ 引理无法推广到有向图上,所以无向图的做法无法移植到有向图。
目前学术界似乎还没有最坏复杂度优于暴力的做法。
另外,[P3238](https://www.luogu.com.cn/problem/P3238) 是个有向图删边最短路模板,然而目前还没有正确性和复杂度都有保障的解法。
### hack1
这个 hack 针对无向图做法直接移植到有向图,属于 hack 正确性。
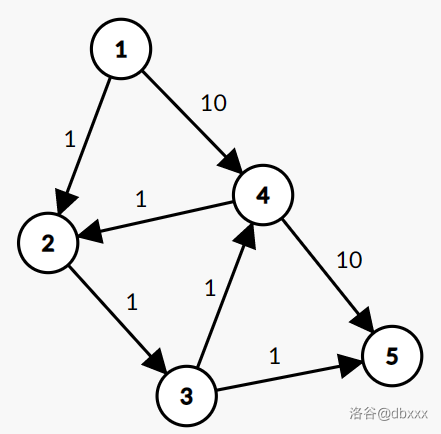
原最短路为 $1 \to 2 \to 3 \to 5$。
考虑删去 $2 \to 3$ 后,删边最短路会变为 $1 \to 4 \to 5$。
不难发现,在原图上,$1 \rightsquigarrow 4$ 的最短路不是 $1 \to 4$ 而是 $1 \to 2 \to 3 \to 4$,$4 \rightsquigarrow 5$ 的最短路不是 $4 \to 5$ 而是 $4 \to 2 \to 3 \to 5$。
因此类似无向图上“一个删边最短路,一定对应着原图上强制经过某 **一条** 非最短路边后的最短路”的结论不再成立。
如果无向图做法移植到有向图,会误判删掉 $2 \to 3$ 后,没有新最短路。
### hack2
这个 hack 针对 SPFA 乱搞,属于 hack 时间复杂度。
下面给出 generator。
```cpp
#include <bits/stdc++.h>
const int N = 20000, M = 4 * N - 1, L = N;
int main() {
printf("%d %d %d\n", N * 2 + 1, M, L);
for (int i = 1; i < N; ++i) printf("%d %d %d\n", i, i + 1, 1);
printf("%d %d %d\n", N, N * 2 + 1, 1);
for (int i = 1; i <= N; ++i) printf("%d %d %d\n", i, i + N, N - i + 1);
for (int i = 1; i <= N; ++i) printf("%d %d %d\n", i + N, i, 1);
for (int i = 1; i < N; ++i) printf("%d %d %d\n", i + N, i + N + 1, 1);
for(int i = 1; i <= L; ++i) printf("%d ", i); puts("");
return 0;
}
```
事实上上面的 $N$ 调成 $5000$ 就足以 hack 掉 P3238 所有 SPFA 乱搞做法。
关于卡 SPFA 就不过多解释了,和本文没啥关系。
### tips
有考虑过暴力吗?
明显地,我们只需要考察某条最短路上的边的删边最短路。但是注意到,最短路的边数不仅不会超过 $m$,而且不会超过 $n - 1$。
因此如果 $n$ 比较小而 $m$ 比较大,我们只需要做 $n - 1$ 次 dijkstra 而不是 $m$ 次。
---
上面的性质告诉我们,影响 $1 \rightsquigarrow n$ 最短路的边不会超过 $n - 1$ 条。
事实上有更强的性质:影响单源最短路的边不会超过 $n - 1$ 条(这里就假设源点为 $1$ 吧)。
也就是说,如果删除 $e$ 之后,只要存在一个 $u$,$1 \rightsquigarrow u$ 的最短路有变,那么就称 $e$ 是有影响的;那么有影响的边不超过 $n - 1$ 条。
为什么?考虑构建以 $1$ 为根的任意一棵最短路树,最短路树上总共只有 $n - 1$ 条边。
最短路树上的边可能有影响,也可能没影响(毕竟最短路树只包含 $1 \rightsquigarrow u$ 的一条最短路径,删了之后可能还有别的最短路径)。
但是,不在最短路树上的边一定是没影响的。所以有影响的边不超过 $n - 1$ 条。
于是你就会做 [P6880](https://www.luogu.com.cn/problem/P6880) 了。这题的原理就是 $n$ 比较小,所以考察删边最短路只需要暴力 $n$ 次 dijkstra。
## 有向无权图
论文科技,非确定性算法,线性根号对数,有兴趣的可以点下面的文章了解:
<https://www.cnblogs.com/Elegia/p/16461398.html>
## 最后
本文的工作量不言而喻。
其实实际工作量是这篇文章的两倍。因为一开始都写完一大篇跟这个差不多字数的解法报告了,结果后来发现那个解法从第二行就开始假……所以只好重新开始。
因此如果觉得这篇文章写得好,解决了你的问题,请不要忘记给个赞!