【学习笔记】点分治
xuyunao
·
·
算法·理论
点分治
点分治从小白到入门?
Update on 2026.1.10:增加了对点分树及点分治性质的补充,并增加了前言后记部分内容。
Update on 2026.1.10:添加了树上均衡路径一题,辛苦管理审核。
前言
我常常追忆过去。
——《追忆》
抬头啊 星空竟是陌生的眼睛
河流啊 带走我被抹去的乳名
有人啊 寻找我眼角的胎记
寻找 候鸟的踪迹
——非弹力碰撞《小孩》
自从 NOIP 之后就一直没有找到一个好的竞技状态,T2 没判相等错失两倍线,虽然当时就已经接受了结果,但是终究还没有调整好,省选模拟赛也没有切出来过题,很摆。与其这样,不如找点事情干,调整一下,尽快找回状态。
在 LCA 课上实在听不懂串串了,找点事情做,想起来当时首都 这题,于是想着把自己做过的一些比较好玩的点分治记录一下,刚好复习一下,语言应该不会很专业很官方,多数是结合自己理解的通俗语言。
什么是点分治
点分治是一种树分治,能解决的是树上路径问题,以我目前的知识水平,只会用点分治解决不定根的问题,更确切来说,点分治无法简单维护祖先关系,因此它不能处理依赖祖先关系的问题。
举个非常抽象的例子(这东西我还真的思考过),你要在一棵 trie 上点分治,但很快就发现这显然是不行的,因为 trie 维护字符串信息,它字符串是有序的,如果进行点分治会使得串的顺序被打乱。可能不那么好理解,后面遇到了自己思考一下就知道为什么不行了。
点分治怎么解决路径问题的
点分治是一个递归分治的过程,简述一下,可以分为下面步骤:
- 找到当前连通块重心,以它作为分治中心
- 递归进入分治中心,统计经过分治中心的路径信息
- 分治中心将当前连通块又划分为若干子连通块,我们对子连通块递归进行上述操作。
由于重心具有良好的性质,最大子树大小不超过 \frac{n}{2},也就是说,我们每递归一层,这个子连通块大小就会减半,因此递归层数为 O(\log n)。由于递归层数有了保证,我们就可以每次从分治中心出发,暴力枚举当前连通块内每个点并统计信息。
分析点分治的时间复杂度,大致可以表示为递归层数 \times 处理每层信息的时间复杂度,递归层数为 O(\log n),处理每层信息就要看具体使用的数据结构,比如线段树或排序就是 O(siz \log siz),总复杂度就是两个乘在一起。
这里要注意,子连通块处理信息需要的复杂度一定是与 siz 有关而不是 n。举个例子,如果你要对子连通块维护值域线段树,那么就需要离散化之后处理,这样才是 O(siz \log siz),要不然每次变成 O(n \log n),总复杂度变成 O(n^2 \log ^2 n),总之点分治处理、清空、维护信息都只能是依赖于当前分治中心的 siz 的。
另外,如果我们把点分治每一层重心向上一层中心连边,这样就会形成一棵树的结构,我们称之为点分树,点分树具有很多优秀的性质:
- 点分树深度为 O(\log n),这意味着我们可以支持暴力枚举祖先。
- 我们定义 siz_u 为点分树上 u 的子树大小,则 \sum siz_u 为 O(n\log n) 级别,不妨考虑对每个点算贡献,每个点的贡献就是祖先数量,而点分树有 O(\log n) 层,于是总的量级为 O(n\log n)。
- 继续上面的结论,记每个分治中心所处理的连通块大小为 siz_u,则 \sum siz_u 也是 O(n \log n) 级别,可以参照上面考虑,这个后面 Tree-MST 那题会用到。
一些例题
说完理论的东西,应该都还不太懂吧,所以找一些例题说一下。
P3806 【模板】点分治 - 洛谷
题意
这是点分治的模板题,给定一棵树,询问是否存在长度为 k 的路径,n \le 10^4,q\le 100,k \le 10^7。
Solution
维护路径信息可以使用点分治,考虑每次找到重心 rt 之后,从 rt 开始 dfs 整个连通块,维护 rt 到每个 u 的路径长度,那么对于 rt 子连通块内的两个点 u,v,他们之间的路径长度 dis(u,v) = dis(rt,u) + dis(rt,v),那么我们维护所有 dis(rt,u),对每个 u 统计答案,问题变成了给定 x,询问是否存在 k - x,这个是好维护的。
但还有一个需要注意的点,点分治要求每一条路径只在深度最高的分治中心被统计到,因此当我们统计信息时,假设 u,v 均位于 rt 的同一子连通块,则需要在后面的分治中心统计,而不能在当前层统计。简单而言,我们要求在 rt 处被统计到的点对 u,v 必须不在同一棵子树。
如何处理这个东西呢?有两种方法:
- 考虑先全都统计上,然后减去每个子连通块内,同样条件下产生的贡献。这里要注意同样条件,例如我们维护路径长度,则当我们对一个子连通块 v 去重,我们需要把 dis[v] 初始化成 w(u,v),也就是我们要在 u 统计答案的情境下,计算 v 子树内产生了多少贡献。
- 也可以用类似 dsu on tree 的合并方式,我们逐个连通块计算答案,先求出该连通块的信息,然后从之前的数据结构中尝试统计答案,统计完当前子连通块后再把当前子连通块内的贡献全都插入数据结构中。
会处理一个分治中心,剩下的就很好做了,只需要找重心,递归下去做就好了。
这里有若干小细节,是我见过刚开始很容易犯的:
- 找重心需要用到一个 mx 数组表示最大子树大小,我们要初始化一下,通常我是写成
mx[rt = 0] = inf。
- 由于 mx 需要考虑原树子树外的那棵子树,因此我们需要
mx[i] = max(mx[i],tot),在这里 tot 表示当前子连通块大小。
- 当我们走一个点 v 时,要时刻注意判断 v 是不是没有递归过,我们给已经处理的分治中心打上标记,判断 v 是否被标记。
- 处理当前分治中心,维护信息大小为 siz 而不是 n。
- 记得每次
getroot 的时候清空 mx。
实现
这里给出我的实现(不一定很优)
int mx[maxn],siz[maxn];
bool vis[maxn];
void getroot(int u,int fa)
{
siz[u] = 1;mx[u] = 0;
for(auto nx : G[u])
{
int v = nx.fi;
if(v == fa || vis[v]) continue;
getroot(v,u);
siz[u] += siz[v];
mx[u] = max(mx[u],siz[v]);
}
mx[u] = max(mx[u],tot - siz[u]);
if(mx[u] < mx[rt]) rt = u;
}
找重心:要注意每次清空 mx,并且每次给 tot 重新赋值,tot 表示当前子连通块大小,同时注意初始化 rt,我一般写成 mx[rt = 0] = inf。如果 tot 赋值错误,并不会导致正确性有问题,但是可能找到错误的重心,导致时间复杂度退化。
void divide(int u)
{
vis[u] = 1;
getans(u);
for(auto nx : G[u])
{
int v = nx.fi,w = nx.se;
if(vis[v]) continue;
tot = siz[v];rt = 0;
getroot(v,u); // 注意这里!!!
getroot(rt,0);
divide(rt);
}
}
divide 分治函数:要注意标记 vis,同时注意打注释的地方,在每次 divide 之前,找完重心都要重新 getroot(rt,0),否则会得到错误的 siz,也就导致 tot 错误,最终使得时间复杂度退化,例如一条链的情况如果不重新 divide 可能出现问题。
const int V = 1e8 + 10;
bool had[V];
int que[maxn],ed;
int dis[maxn],cnt;
void dfs(int u,int fa,int d)
{
dis[++cnt] = d;
for(auto nx : G[u])
{
int v = nx.fi,w = nx.se;
if(vis[v] || v == fa) continue;
dfs(v,u,d + w);
}
}
void getans(int u)
{
had[0] = 1;ed = 0;
for(auto nx : G[u])
{
int v = nx.fi,w = nx.se;
if(vis[v]) continue;
cnt = 0;dfs(v,u,w);
for(int i = 1;i <= cnt;i++)
for(int j = 1;j <= m;j++)
if(q[j] >= dis[i]) ans[j] |= had[q[j] - dis[i]];
for(int i = 1;i <= cnt;i++) had[dis[i]] = 1,que[++ed] = dis[i];
}
for(int i = 1;i <= ed;i++) had[que[i]] = 0;
}
getans 部分:这里给出的是第二种去重方式,也就是每次先算贡献,再插入到数据结构中,避免同一子连通块产生贡献。要注意每次情况都是 O(size) 的,而第一种去重方式由于每次去重都要递归所有子树,会导致常数较大。
请注意,在这篇文章中的代码有一些可能只写了一次 getroot,因此请注意自己修改!!!
针对这题还有一个需要注意的点,边权 w \le 10^4,n \le10^4,路径信息是可能到达 10^8,因此要么开数组开到 10^8,要么在信息超过 10^7 时直接 continue。
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin >> n >> m;
for(int i = 1;i < n;i++)
{
int u,v,w;cin >> u >> v >> w;
G[u].push_back({v,w});
G[v].push_back({u,w});
}
for(int i = 1;i <= m;i++) cin >> q[i];
mx[rt = 0] = inf,tot = n;
getroot(1,0);
getroot(rt,0);
divide(rt);
for(int i = 1;i <= m;i++) cout << (ans[i] ? "AYE\n" : "NAY\n");
return 0;
}
最后主函数:要注意的是初始化 rt,mx,tot 以及在 divide 以前进行两次 getroot 从而求出正确的子树大小信息。这里还有一个小细节,我们可以将所有询问全都输入然后在每次分治过程中更新答案。
全部实现
复杂度分析
我们分析一下复杂度,点分治递归层数 O(\log n),对于每个分治重心,统计答案 O(m \times size),总复杂度为 O(nm\log n),但我们要注意,点分治需要递归,常数是非常大的,因此如果我们在每次输入询问后都进行一次点分治,这个大常数是要乘上 m 的,可能会导致被卡常。
P4178 Tree - 洛谷
题意
询问树上长度 \le k 的路径数量,n \le 4 \times 10^4,k \le 2 \times 10^4。
Solution
非常板的一题,考虑像上一题一样,维护从分治中心出发到每个点的路径长度,那么要找 \le k,我们可以直接排序双指针统计答案,这份代码使用的是第一种去重方法,也就是对于子树重新 getroot 并减掉。
代码
CF293E Close Vertices - 洛谷
这题可以说是上一题加强版了。
题意
询问树上边数 \le l 且边权值和 \le w 的路径数量。
#### Solution
在上一题基础上,变成了两维的限制,那么我们不仅需要维护路径长度,还需要维护边权和,相当于对于每个点有一个二元组 $(x,y)$,那我们考虑说,对其中一维做双指针,另一维用数据结构维护,这里使用了树状数组,然后就做完了,复杂度 $O(n \log^2 n)$。
[完整实现](https://codeforces.com/contest/293/submission/329160207)
### [U648884 MX-BJ 树上均衡路径 - 洛谷](https://www.luogu.com.cn/problem/U648884)
#### 题意
已经很简化了,直接粘了。
如果树上一条简单路径满足:路径上点权最大值和最小值**都**在路径的端点上,并且**路径的两个端点不相同**;那么称之为完全非均衡路径。
给定一棵树,点权就是点的编号(是 $1$ 到 $n$ 的排列),求这颗树上的完全非均衡路径数量。
$n \le 5 \times 10^5$。
#### Solution
[A_zjzj ](https://www.luogu.com.cn/user/263082) 讲解的模拟赛,正解等下再写,这题点分治其实是歪解,但倒也是正解。
这种路径计数问题一看就非常可以点分治,我们考虑维护出从分治中心出发到树上每个点路径的最大值和最小值,限制就是 $mx_u = u$ 或者 $mi_u = u$。那么具体维护,类似上面那个,我们可以把 $mx$ 或者 $mi$ 分别维护到树状数组上,然后查询一段后缀 / 前缀就好。
这里要注意,对于从分治中心出发的一条路径需要单独处理一下,其实加个二分答案就好了,二分一下它作为 $\max$ 和 $\min$ 能配对的点,计算上贡献就好。点分治做法总复杂度 $O(n \log ^2 n)$,带有大常数。
下面是正解给出的做法。
分别建出最小、最大生成树的 Kruskal 重构树(注意这里是关于点的重构树),此时一条路径 $(u,v)$ 满足条件等价于在一棵重构树上要求 $u$ 是 $v$ 的祖先,在另一棵重构树上 $v$ 是 $u$ 的祖先。
考虑在第一棵重构树上 DFS,走到 $v$ 时,$v$ 到根链上的点可以成为 $u$。可以维护到根链的信息,DFS 进入 $v$ 时在第二棵树上加入 $v$,回溯时删掉 $v$,对于点 $v$ 查询在第二棵树上有多少个点是 $v$ 的后代即可,可以用树状数组维护单点加子树和,时间复杂度 $O(n\log n)$。
后面这一段是粘的题解,但是其实说到底就是一个二位偏序的限制,这个部分后面还会再研究。
#### 实现
当时实现的很烂,忘记处理从分治中心出发的路径了,而且后面二分搞混了很多变量名,需要精细实现一下,同时由于当时 mx 机子太慢了,所以加了非常多卡常,可能导致代码可读性下降。
[场上代码](https://www.luogu.me/paste/zymmmmfc)
## 几个需要思考的题
### [P12491 [集训队互测 2024] 串联 - 洛谷](https://www.luogu.com.cn/problem/P12491)
这也是我的第 1000 道题~~本来想写追忆~~,点分治真好玩。
#### 题意
没有形式化了,粘一下原题面吧。
给定一棵树,每个点有两个权值 $a_i,b_i$。对于树上的一条简单路径,若这条路径上 $b$ 之和乘上 $a$ 的最小值大于等于一个常数 $V$,那么这条路径被称作一条好的路径。
即:对于一条简单路径,设 $p_1,p_2,\dots,p_k$ 为路径上的点。这条简单路径是好的,当且仅当 $\min_{i=1}^k a_{p_i} \times \sum_{i=1}^k b_{p_i}\ge V$。
求所有好的路径中,$\sum b$ 的最小值。
$n \le 2 \times 10^5$,$V \le 10^{18}$,$a,b \le 10^9$。
#### Solution
一个比较板的点分治,难点在于如何统计答案。
我们观察这个式子,发现处理路径问题,路径 $\sum$,路径 $\min$ 都能用点分治维护,考虑能不能点分治,如何对每个分治中心统计答案。
首先考虑这个 $\min$ 对于一条路径拆开处理,首先维护从分治中心到每个点的路径 $\min a$ 以及 $\sum b$,我们设他们为 $A,B$。考虑按照这个 $A$ 从大到小插入,这样当前插入的 $A$ 一定作为较小值,去掉了 $\min$ 的限制。
接下来就很简单了,相当于是询问我们最小的 $B_j$ 满足 $B_j \geq \lceil \frac{V}{A} \rceil - B - b_{rt}$,把这个东西维护到值域上,求后缀 $min$ 即可。这里要注意要对值域离散化处理,要不然每次复杂度 $O(V)$ 就寄了,或者其实可以记录一下加进去了啥,然后清空掉也是可以的。
这里要注意,我们要求统计的答案不属于同一子连通块,因此我们还需要维护一下后缀非同一子树的次小,从而避免同一棵子树的情况。
注意单点也算一条路径,分治中心到一个点 $x$ 同样也是一条路径,需要特殊计数一下单点和这种路径,但是需要分清,究竟是处理的单点情况还是这样的路径,否则你就会像我一样以为自己处理了两种,实则只处理了单点。
[完整实现](https://www.luogu.me/paste/x15i3gvo)
### [P7215 [JOISC 2020] 首都 - 洛谷](https://www.luogu.com.cn/problem/P7215)
这是极其好的一道题,可以帮助我们深刻理解点分治的一些不易察觉的东西,嗯,感受那股劲就对了。~~我不会告诉你当时模拟赛搬了这个题发现自己之前根本没搞懂。~~
这题可以帮你深刻理解点分治,它能够具有哪些性质,而又不具有哪些性质。
#### 题意
给定一棵 $n$ 个点的树,每个点有颜色,共 $k$ 种颜色。定义一次操作:将一种颜色的所有点都改成另一种颜色。
现在你要进行若干次操作,使得操作之后你能够选出一种颜色 $c$,使得只保留颜色为 $c$ 的点和他们之间的边,这些点是联通的,询问最小操作次数。
$n,k \le 2 \times 10^5$。
#### Solution
这题有两种做法,我们先来考虑这样一个性质,对于一种颜色 $x$,如果 $c_i = x$ 的两个点 $u,v$ 路径上经过了一个颜色为 $y$ 的点 $p$,则如果我们最终选择颜色 $x$,就必须把颜色 $y$ 变成 $x$,同理不断扩展。
这样我们可以搞出一个拓扑序,表示如果选 $x$ 就必须选 $y$,那么最终答案就是要找到出度为 $0$ 的强连通分量的点数最小值,用线段树优化建图或者倍增优化建图可以做到 $O(n\log^2n)$,但是由于点分治巨大的常数,这个是可以跑过点分治的。
接下来我们考虑点分治怎么做~~我也不知道怎么想到点分治的~~,我们考虑最终选择分治中心这个颜色,只考虑当前连通块内的点,也就是维护一个队列,将需要改变颜色的点都搞进来,假设出现了该子连通块以外的点,那么直接退出。
我们来说明一下为什么出现子连通块外的点可以直接退出,考虑这样一个事情,假设当前分治中心颜色为 $x$,出现了一个需要修改的颜色 $y$,且 $y$ 同时出现在了当前子连通块内外,为了让当前情况合法,就必须让这两个 $y$ 最终联通,那么这两个 $y$ 之间路径上所有点都需要被修改。
而由于另一个 $y$ 在当前子连通块外,因此他们会在更高的分治中心被统计到,于是我们需要直接退出,因为在 $x$ 统计只会比在更高层统计不优(考虑除了前面要选的那些,我们又多选进去了 $x$ 这种颜色)。
------
这时候有好奇宝宝就要问了(其实就是我):如果子连通块内外同时出现了一个 $y$,按照树上问题来考虑,子树内外两个点,他们路径不是一定会经过根 $x$ 吗?这样不就变成选 $y$ 必须选 $x$,$x$ 就更优了。
**非也!**
这里我们就要阐述一下了,点分治只能保证点与点之间的路径和连通性不变,至于原树上的边,和点分治每一层的点之间没有任何关系,因此我在形容的过程中,一直使用了 **子连通块** 的字样而不是子树,这里一定要注意。
不懂得可以看下面的图,图中红色点为当前分治重心,绿色点为一个更高层的分治中心,蓝色圈出的是当前分治中心处理的子连通块,紫色的是两个颜色为 $y$ 的点之间的路径。
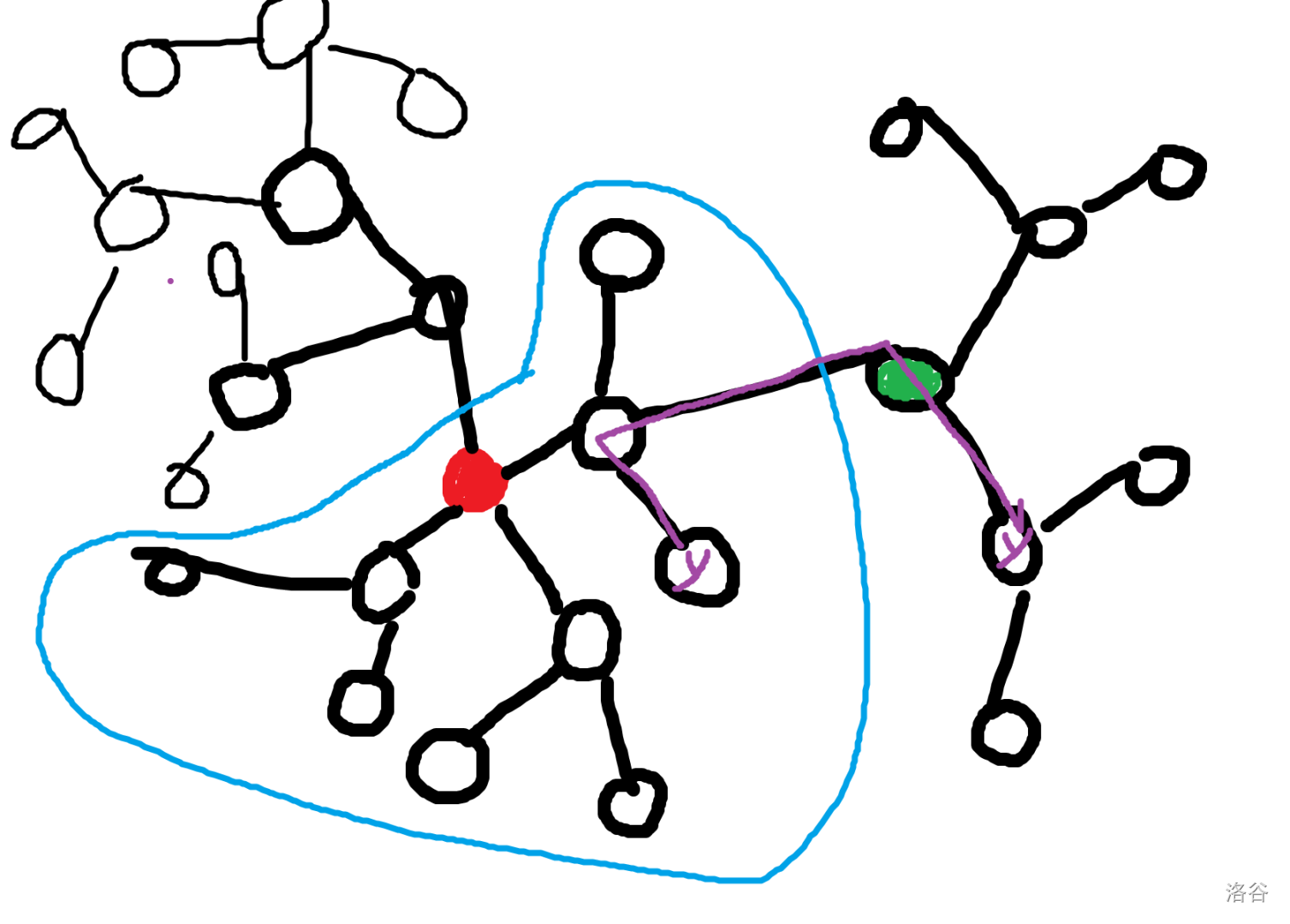
先来简单解释一下,对于没被围起来的部分,说明他们层次更高,在前面已经被处理过了,可以尝试自己这样子画图理解一下,这样的图非常适合点分治(还是从 [ez_lcw](https://www.luogu.com.cn/user/118318) 课上学到的),不难发现这两个 $y$ 之间路径是在绿色点被统计到的,也没有经过当时分治中心。
对于点分治,我们只能保证,对于当前连通块的几个子连通块之间的路径,一定经过当前分治中心,也就是红点把蓝色部分分成的几个子连通块之间的边,是一定经过红色点的,而蓝色内外是不一定经过红点的。
[完整实现](https://www.luogu.me/paste/sz1ysztu)
### [AT_cf17_final_j Tree MST - 洛谷](https://www.luogu.com.cn/problem/AT_cf17_final_j)
这个题,有点难,甚至于当时 ez_lcw 上课现场没有想出最简单的做法,现在暂时忘记怎么做的了,后面有时间可能会学习一下视频补上 lcw 讲解的做法。
#### 题意
给定一棵 $n$ 个点有边权的树,每个点有一个权值 $x_i$,考虑这 $n$ 个点构成了这样一张完全图 $G$,满足对于任意 $u,v$,两点之间连边的边权 $w(u,v)$ = $x_u + x_v + dis(u,v)$,这里 $dis(u,v)$ 表示树上 $u,v$ 两点之间的距离。
#### Solution
我们首先来考虑这样一个性质(貌似神秘 B 算法求 MST 就是用了这个):
> 对于稠密(完全)图 $(V, E)$ 求 MST,可将 $E$ 分成 $E_1, E_2, \dots, E_k$,满足其并集为 $E$,对每个边集求 MST(可以不连通),再将得到的边集再求一次 MST,即为原图的 MST。
有了这个性质,又发现边权与树上距离有关,考虑拆开,发现可以拆成两段,也就是边权变成了 $(dis(rt,u) + x_u) + (dis(rt,v) + x_v)$。
这个形式,很难不想到点分治,我们考虑以当前分治中心,处理出每个点的这个值,我们称他为 $val_i$,那么该子连通块的 MST,也就相当于从所有的 $val_i + val_j$ 中取,使得总和最小。
发现每个点的 $val$ 是必须取到的,那就另一个直接取最小值就好了,因此我们直接维护一下最小的 $val_i$,然后把每个点都向这个最小的点连边,直接用 vector 把所有边存起来,最后在外面做一遍 Kruskal 就是对的,正确性可以由上面的性质得知。
而这样做的时间复杂度呢?我们来分析一下。
对于每个分治中心,它所产生的边数是 $O(size)$ 级别的,那么对于整个过程所产生的总边数是 $O(n \log n)$ 级别的,于是我们直接再做 Kruskal,总复杂度 $O(n \log^2 n)$。
[提交记录](https://atcoder.jp/contests/cf17-final/submissions/72315712)
### [P12480 [集训队互测 2024] Classical Counting Problem - 洛谷](https://www.luogu.com.cn/problem/P12480)
这题好啊,可以让我们知道点分治用法其实很灵活,我直接搬题解了。
扫描线 $+$ 点分治,你值得拥有!
#### 题意
给定一棵 $n$ 个点的树,可以进行以下操作:
- 选择当前树上编号最大或最小的点,删除它以及以它为端点的所有边,并任选一个连通块作为新的树。
- 记 $\min$ 为当前树上编号最小值,$\max$ 为当前树上编号最大值,$size$ 为树上节点数量。定义一棵树的权值为 $\max \times \min \times size$,求能通过上述操作得到的非空树的权值和,答案对 $2^{32}$ 取模。
#### Solution
拿到题目,很难找到入手点,因此我们先来考虑一个性质:
- 一个 $\min$ 和一个 $\max$ 能够确定唯一的树。
我们考虑它的条件,$l,r (l \le r)$ 能确定一棵树的充要条件是,$l,r$ 路径上所有点编号都在 $[l,r]$ 之间。若不在则 $l,r$ 不能够作为 $\min$ 和 $\max$,否则可以从这条路径不断向外扩展,直到边界 $<l$ 或边界 $>r$,于是我们确定出一棵唯一的树。
此时我们容易得到一个 $O(n^3)$ 的做法,枚举 $l,r$,并 check $l,r$ 能否构成一棵合法的树。固定其中一个,移动另一个就可以做到 $O(n^2)$,可能需要带个 $\log$。
发现还需要继续优化,考虑拆贡献,可以将权值中的 $size$ 拆开,拆成对所有合法的 $(l,r,x)$ 三元组计算贡献,每个三元组的贡献就是 $l \times r$。问题转化为求树上有多少三元组 $(l,r,x)$,满足 $l,r$ 能确定一棵树并且 $x$ 位于 $l,r$ 确定出的树上。
考虑 $(l,r,x)$ 的关系大概是像下图中这样,按照 [ez_lcw](https://www.luogu.com.cn/user/118318#main) 课上讲的名字,称之为 “风车形”。
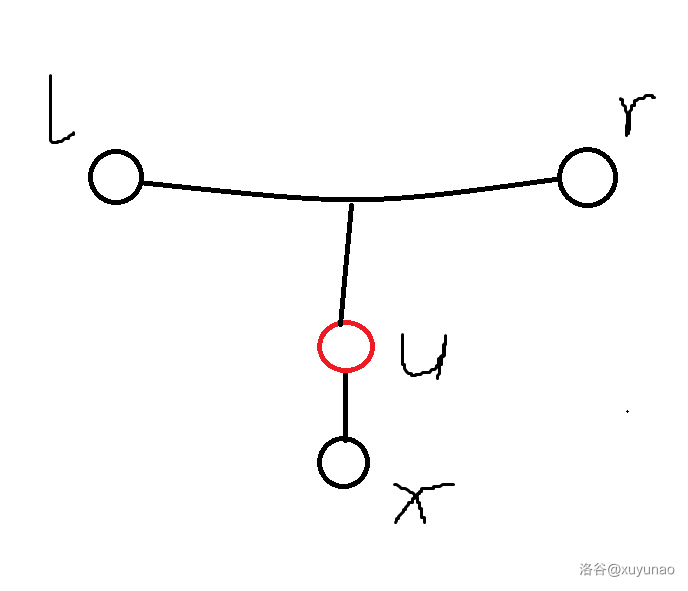
考虑点分治,对于每个风车,在风车上所有点中,点分树上深度最小的点上统计答案。假设红色点 $u$ 是统计答案的分治中心,需要满足 $l,r,x$ 均位于 $u$ 在点分树上的子树内,且其中至少两个点不在同一棵子树,也就是下图的两种情况。
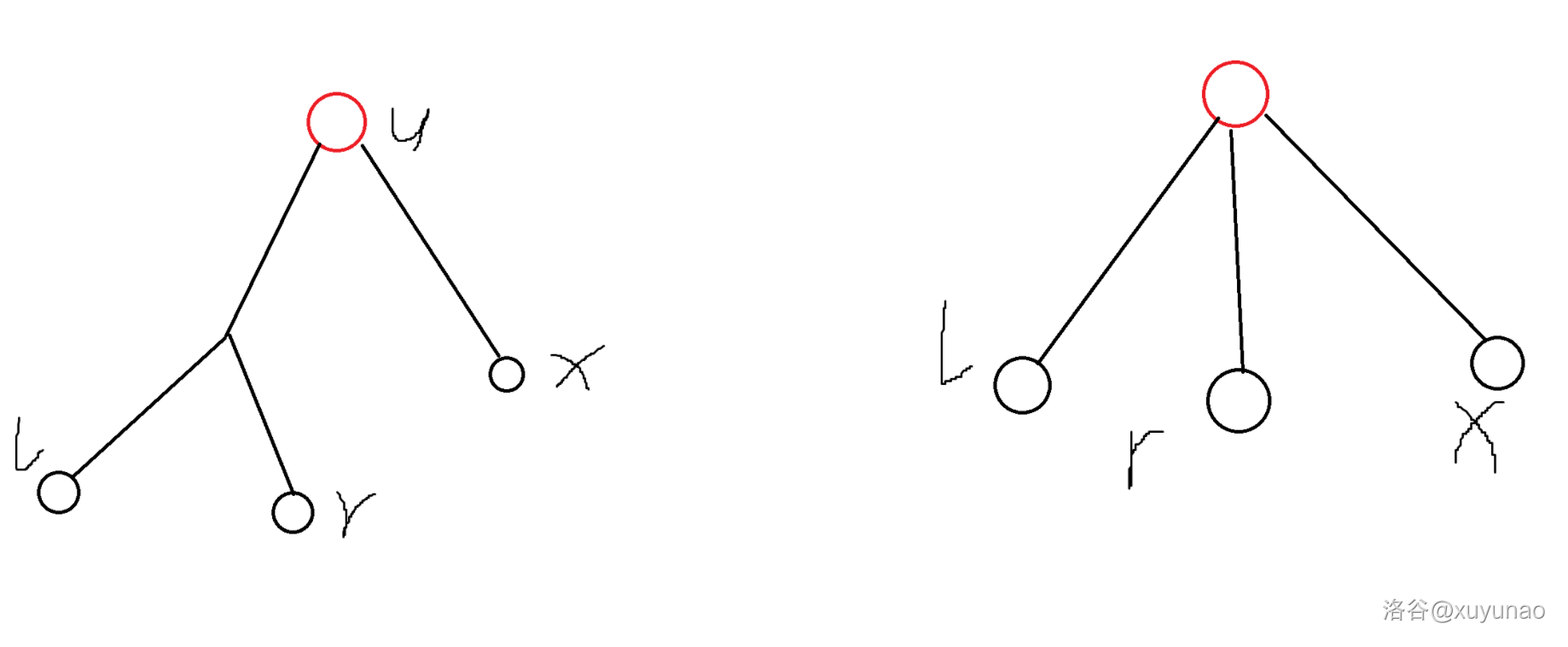
其中 $u$ 是这个风车上,点分树上深度最小的点。
接下来问题变成,我们如何统计子树内所有 $(l,r,x)$ 三元组的贡献,我们设 $mi_u$ 表示从分治中心到 $u$ 的路径上最小值,$mx_u$ 表示从分治中心到 $u$ 路径上的最大值,首先可以发现合法的 $l,r$ 满足 $mi_l = l,mx_r = r$。
$$\begin{cases} mx_l \le r \\ mx_x \le r \\ mi_x \ge l \\ l \le mi_r \end{cases}$$
考虑扫描线,对于每个 $r$ 处统计答案,统计合法的 $(l,x)$ 对的贡献。
考虑该怎么处理得到的限制关系。把子树内每个点 $u$ 维护在 $mx_u$ 的位置,从前往后扫描线,这样我们就解决了前两条限制关系。考虑维护一棵线段树,线段树需要维护三个信息:
- 对于每个位置 $i$,$l = i$ 的 $l$ 的编号和 $sum$。
- 对于每个位置 $i$,$mi_x = i$ 的 $x$ 的数量 $cnt$。
- 对于每个位置 $i$,$l = i$ 的合法 $(l,x)$ 对的贡献和 $val$。
那么对于每个限制 $4$,也就是 $l \le mi_r$,相当于是在一段前缀 $[1,mi_r]$ 查询合法 $(l,x)$ 对贡献,我们把拆完的贡献中的 $\times min$ 在这里计算。
接下来考虑如何统计 $(l,x)$ 对的数量,这里就要用到第三条限制关系,考虑加入一个点,这个点作为 $x$ 和作为 $l$ 的情况。
- 这个点作为 $x$,此时对于 $l \le mi_x$ 的所有 $l$,$x$ 都能与之配对产生贡献。对于所有合法的 $l$,它能增加的贡献值也为 $l$,要对这些 $l$ 的 $val$ 加上他们对应的 $sum$。同时插入 $x$ 后,$mi_x$ 处的 $cnt$ 也要 $+1$。
- 这个点作为 $l$,此时我们需要计算这个 $l$ 能和多少 $x$ 产生贡献,发现就是询问 $mi_x \ge l$ 的 $x$ 的数量,由于前面我们对每个位置 $i$ 维护了 $mi_x = i$ 的 $x$ 的数量,这里可以直接区间查询,同时 $l$ 位置的编号和也需要增加。
对于第一类,我们需要对贡献值区间加对应的 $val$,同时需要区间查询 $val$,因此需要线段树维护 $val$ 区间加,区间求和。同时需要对 $cnt$ 单点加,因此需要维护单点加的 $cnt$。
对于第二类,需要询问区间 $cnt$ 和,对 $cnt$ 线段树维护区间和,同时需要对 $sum$ 单点加,因此对 $sum$ 维护单点加区间查。
想通如何维护之后这道题目就很简单了,实现不难,维护出需要的信息即可。每层维护线段树,复杂度为 $O(m \log m)$,其中 $m$ 为点的数量,总复杂度 $O(n \log ^ 2 n)$。
#### 实现细节
- 注意到模数是 $2^{32}$,可以直接使用 unsigned int 存储,这样就不需要取模了。
- 对于每层值域需要离散化,否则每层都是 $O(n\log n)$ 的,总时间复杂度会变成 $O(n^2 \log^2 n)$。
- 要先加入 $l,x$,再询问 $r$。
- 由于需要去重,如果对每棵子树减去贡献,注意路径 $\min$ 和 $\max$ 的初始值。
- 该清空的要清空,该赋值的要赋值。
[完整代码](https://www.luogu.com.cn/record/256944292)
## 后记
本文使用 Typora 编写,如有格式问题影响阅读请谅解。
点分治真好玩!应该有新的比较好的题还会加进来。
省选 2026 rp++!
> 我该在哪里停留?我问我自己。
>
> ——《追忆》
>
> 有一天 阳光照进冰冷的河里
> 有一天 藤蔓爬上了云梯
> 你听啊 让风代替我喊你
> 知道 你从未放弃
>
> ——非弹力碰撞《小孩》