CF 高分段题目总结
_sys
·
2021-02-11 10:34:05
·
个人记录
1508D Swap Pass
给定平面上 n 个点,第 i 个点坐标为 (x_i,y_i) 点权为 a_i 。
你可以执行以下操作若干次:
选择两个不同的下标 i,j ,交换 a_i,a_j ,然后以点 i 点 j 为两端点画出一条线段。
要求最终形成的图中不存在相交线段(交于端点处不认为相交,相同线段认为相交),并且满足 a_i=i 。
给出任意一种方案或者报告无解。
***
[评测链接](https://codeforces.com/contest/1508/submission/114405430)
我好像秒了。
考虑 $a$ 构成了一个环怎么做。
我们随便选一个点,连一棵菊花,然后一个一个换。
多个环,我们随便选一个点满足 $a_i \neq i$,然后连一棵菊花。之后我们把所有点按照极角排序。如果两个相邻的点不在同一个环里,就先把他俩交换,这样他俩就在一个环内了。直到最后全到一个环里。
# [1491H Yuezheng Ling and Dynamic Tree](https://codeforces.com/problemset/problem/1491/H)
给定一棵大小为 $n$ 的 $1$ 为根节点的树。
接下来有两种操作:
- `1 l r x` 令 $a_i=\max(a_i-x,1)$($l\leq i\leq r$)。
- `2 u v` 查询在当前的 $a$ 数组构成的树上 $u,v$ 的 LCA。
$2\leq n,q\leq 10^5$,$1\leq x\leq 10^5$。
***
简单 Ynoi 题。我好像秒了。
考虑假如树高小于根号,那询问的复杂度就能接受。
如果树高大于根号,修改的次数不会很多就小于根号了。
具体地,我们对序列分块。同一个块内若一步到了下一块,那很好,查询的时候暴力跳即可。
否则我们预处理每个点跳出块会跳到哪。
由于每个块执行至多 $\sqrt n$ 次就一步跳出去了,所以总复杂度是 $O(\sqrt n^3)=O(n\sqrt n)$。
零散块暴力,复杂度 $O(q \sqrt n)$。
之后看题解说这就是弹飞绵羊,好像确实,看来我记性确实差。
# [1458D Flip and Reverse](https://codeforces.com/problemset/problem/1458/D)
给定一个 $01$ 串,每次可以选择一个连续子序列,满足 $0$ 的个数和 $1$ 的个数相同,将其翻转后取反。求能够得到的字典序最小的串。$|S| \leq 5\times 10^5$。
***
[评测链接](https://codeforces.com/contest/1458/submission/102100418)
我们把 $0$ 看作 $-1$,求串的前缀和 $s$。
我们构建有向图 $G$,$i$ 号点表示前缀和为 $i$。$(u, v)$ 有边当且仅当存在 $i$ 使得 $s_i = u, s_{i + 1} = v$。
这样,操作的条件就变为:从一个点出发,走若干步,回到起点。
操作的效果就变为:将一条回路的所有边方向取反。
那么所有能得到的串为 $G$ 变为无向图后,访问点的顺序差分(因为我们做了前缀和)。很显然地,前缀和的字典序越小,原序列的字典序也越小。
# [1416F Showing Off](https://codeforces.com/problemset/problem/1416/F)
对于大小为 $n\cdot m$ 的矩阵 $A$ 和 $B$,其中 $A$ 的每个元素为一个权值 $w(i,j)$,$B$ 的每个元素为一个方向 `L/R/D/U`,表示能走的方向。定义 $S_{i,j}$ 表示从 $(i,j)$ 出发能够到达的点的 $A_{i,j}$ 的和。给定矩阵 $S$,构造 $A$ 和 $B$ 使得其生成的矩阵为 $S$。$1\le n\cdot m\le 10^5$。
***
[评测链接](https://codeforces.com/contest/1416/submission/104945320)
$B$ 构成了基环内向森林。对于一个环上的点,他们的值应该相同。由于在网格图上,所有的环应该为偶环。
对于一种方案,我们把所有的环可以拆成若干个大小为 $2$ 的环,显然,这样也是合法的,并且更方便我们构造。
若一个位置的权值小于等于四周所有权值,那它只能是环边。
我们把所有相邻且权值相同的点对连边,最后的方案是这张图的一个匹配。由于存在强制选择的点,所以我们使用上下界网络流。
由于网格图是二分图,网络流的时间复杂度为 $O(|V|\sqrt {|V|})$。
# [1416E Split](https://codeforces.com/problemset/problem/1416/E)
给出长度为 $n$ 的序列 $a_i$,求长度为 $2n$ 的正整数序列 $b_i$ 满足:
- $\forall i\in[1,n],b_{2i-1}+b_{2i}=a_i$;
- 满足上述条件基础上,将 $b$ 的值域连续段缩成一个数,要求 $b$ 的长度尽可能小。
求这个最小长度。$n \leq 10^5$。
***
[评测链接](https://codeforces.com/problemset/problem/1416/E)
难题。
正整数很烦,我们先把 $b$ 整体 $-1$,这样每个 $a$ 就要 $-2$。
们发现,若 $b_{2i}\neq b_{2i+1}$,那我们就能把 $[1, i], [i+1, n]$ 分成两个独立的子问题。这是我们 dp 的阶段。
对于每一个阶段,我们需要保证所有 $b_{2i}=b_{2i+1}$。
设 $w_{i, j}$ 为 $a_{i+1 \ldots j}$ 满足上述条件下的答案,若无解为 $+\infty$。接下来我们考虑如何计算 $w_{i, j}$。
若我们确定了 $b_{2i+1}$,那么 $b_{2i+2\ldots 2j-1}$ 都能推出。并且他们为线性关系($b_{2k-1}$ 增加 $1$,$b_{2k},b_{2k+1}$ 减少 $1$,$b_{2k+2,2k+3}$ 增加 $1$,$b_{2k+4,2k+5}$ 减少 $1$,$\ldots$ ),由此,我们能够得出 $b_{2i+1}$ 的取值范围 $[l,r]$。并且,在若干个特殊的取值上,我们能将答案减少 $1$(存在一个 $b_{2k-1}=b_{2k}$,我们倒推回去得到这个特殊的位置)。
我们令 $b_1=x$,对于每个位置,求出合法的区间 $[l_i, r_i]$,令 $z_{i, j}$ 为 $\bigcap_{j < k \leq i} \left[ l_k, r_k \right]$。可以发现,$z_{i, j}$ 平移可得到 $w_{i, j}$,所以我们直接考虑 $z_{i, j}$。
设 $\delta_{x, i, j}$ 表示区间 $[i, j]$,$b_1$ 取值为 $x$ 时 $b_{2k-1}=b_{2k}$ 的个数。$f_i$ 表示 $[1, i]$ 的答案。则有:
$$f_i = \min_{0 \leq j < i} \left( f_j + \left( i - j + 1 \right) - \delta_{j, i} \right) = i + 1 + \min_{0 \leq j < i} \left( f_j - j - \delta_{j, i} \right)$$
考虑维护 $f_j-j-\delta_{j, i}$。
当 $i-1\to i$ 时,首先有 $[l_i, r_i]$ 的限制,所以 $[1,l_i)$ 和 $(r_i,+\infty)$ 的值要清空(赋值为 $+\infty$)。
其次,我们可以从 $f_{i-1}-(i-1)$ 转移,所以有全局取 $\min$。
之后,还会有一个特殊的位置 $\frac {a_i}2$ 使得 $\delta$ 改变,即单点减一。
最后,我们需要查询全局最小值。
线段树维护即可。
# [1392H ZS Shuffles Cards](http://codeforces.com/problemset/problem/1392/H)
有 $n+m$ 张牌,其中前 $n$ 张牌上分别标着 $1,2,\cdots,n$ 的数字,后 $m$ 张牌是鬼牌。现在我们打乱这些牌,然后开始抽牌游戏,每一轮你可以抽一张牌:
- 如果抽到了一张标有数字 $x$ 的牌,就移除这张牌,并将 $x$ 加入一个集合 $S$ ;
- 如果抽到了鬼牌,就把移除的牌重新加入牌堆,再次打乱所有牌的顺序,重新开始抽牌。如果你抽到了鬼牌,并且集合 $S$ 已经包括了 $[1,n]$ 中全部 $n$ 个数,那么抽牌游戏结束。
询问抽牌游戏结束的期望轮数。
***
[评测链接](https://codeforces.com/contest/1392/submission/101997176)
计数题,咕。
# [1383F Special Edges](https://codeforces.com/problemset/problem/1383/F)
给定一张 $n$ 个顶点,$m$ 条边的有向图 $G$,其中每条边有一个非负整数的容量。其中有 $k$ 条边是特殊的,它们在原图中的编号为 $1$ 到 $k$。在初始情况下它们的容量均为 $0$。
现在有 $q$ 组询问,对于每组询问,会给定 $k$ 个非负整数 $w_1, w_2, \ldots, w_k$,你需要求出:如果将编号为 $i$ 的特殊边的容量改为 $w_i$ (对 $i=1,2,\ldots,k$),那么从 $1$ 到 $n$ 的最大流会是多少?
$n, m \leq 10^4$,$q\leq 2\times 10^5$,$k \leq 10$,$w \leq 25$。
***
[评测链接](https://codeforces.com/contest/1383/submission/105067903)
考虑转化为最小割。
我们枚举这 $k$ 条边有哪些边被割了。
剩下的边不能被割,所以边权设为 $+\infty$,其余边设为 $0$,与 $G$ 一起跑最小割。
对于一个询问,答案为 $\min_{S}\{\sum_{i \in S}w_i+\textrm{mincut}(S+G)\}$。
这样的复杂度是 $O(2^k(\textrm{mincut}(G)+q))$ 的,不能接受。
考虑 $w$ 只有 $25$,所以退流的复杂度为 $O(25m)$,我们可以构造一个格雷码进行枚举,这样每次只有一次加边/删边,可以由之前的状态转移。
我用的方法是通过 $\textrm{popcnt}$ 分成若干个阶段转移,每次把 $\textrm{popcnt}$ 相同的全部存下来。
时间复杂度:$O(2^k(25m+q))$。
# [1338E JYPnation](https://codeforces.com/problemset/problem/1338/E)
给定一张 $n$ 个点的**竞赛图**,满足图中不存在一个三元环的三个顶点连向同一个点,求每对点之间的距离之和,若无法到达,贡献为 $514n$。
$n \leq 8000$。
***
[评测链接](https://codeforces.com/contest/1338/submission/105646804)
首先,这样的图的形态为:一条链,链上最后一个点连向一个强连通分量。因为若存在两个大小大于 $1$ 的强连通分量,必然是不合法的。
若 $(u, v)$ 中有一点在链上,那么计算是十分容易的。
考虑 $(u, v)$ 都在强连通分量里的情况,可以证明,$\textrm{dis}(u, v) \leq 3$。
考虑 $(u, v)$ 的最短路 $(d_1, d_2, \ldots, d_k)$,$d_1=u, d_k=v$,必须满足不存在 $d_i \to d_j$($j-i > 1$),否则会和最短路的定义相悖。
所以有 $d_{k-2} \to d_{k-1},d_{k-1}\to d_{k}, d_k \to d_{k-2}$,若 $k > 4$,则有 $d_k \to d_1, d_{k-1}\to d_1,d_{k-2}\to d_1$,这是不合法的。所以 $k \leq 4$ 也即 $\textrm{dis}\leq 3$。
$\textrm{dis}=1$ 的点对数就是边数。我们只用求出 $\textrm{dis}=2$ 的点对数。
$\textrm{dis}(u, v)=2$ 的条件是:$u$ 的出边集合与 $v$ 的入边集合有交。
考虑 $u$ 的出边集合里的两个点 $(x, y)$,$x \to y$。
则有:$v \to u, u \to x, u \to y,x\to y$。若 $x \to v$,则 $y \to v$,否则存在不合法的 $(u, v, x)\to y$。
所以若 $x \to y$,我们就不用再考虑 $x$ 了。我们只用找到 $u$ 出边集合中,拓扑序最靠后的点判断即可。
复杂度:$O(n^2)$。
# [1336F Journey](https://codeforces.com/problemset/problem/1336/F)
给定一棵树和 $m$ 条链,求多少对链的交中包含的边数 $\geq k$。
***
[评测链接](https://codeforces.com/contest/1336/submission/94529912)
很麻烦,详见[题解](https://www.luogu.com.cn/blog/sysjuruo/solution-cf1336f)。
# [1326F2 Wise Men (Hard Version)](https://codeforces.com/problemset/problem/1326/F2)
有 $n$ 个人。给出 $n$ 个人的「认识情况」(双向且保证合法)。
定义 `bool` 值函数 $K(i,j)$ 表示两个人是否认识。考虑一个 $n$ 个人编号的排列 $p$ ,定义其生成的 $01$ 串 $\{s_{n-1}\}$ 为 $\forall i\in[1,n-1]\cap\mathbb{Z_+},s_i=K(p_{i},p_{i+1})$。
统计对于 $2^{n-1}$ 种不同的 $01$ 串,有多少种排列可以生成它。
$2\leq n\leq 18$。
***
[评测链接](https://codeforces.com/contest/1326/submission/105640348)
计数题,咕。
# [1307G Cow and Exercise](https://codeforces.com/problemset/problem/1307/G)
给出一个 $n$ 个点 $m$ 条边的**有向图**,每条边有边权 $w_i$ 。
有 $Q$ 次询问,每次询问给出一个 $x$ 。你可以把一条边修改成 $w_i+a_i$ ($a_i$ **不一定**是整数),不过需要保证 $a_i \geq 0$ 且 $\sum a_i \leq x$ 。
你要通过修改边权使得从 $1$ 到 $n$ 的最短路径尽可能长,每次询问之间**独立**。
***
[评测链接](https://codeforces.com/contest/1307/submission/88135945)
若 $x \to +\infty$,则我们需要不存在一条 $1\to n$ 的路径满足路径上没有边被扩大,并且还需要选择的边尽可能少。
设原图每条边单位边权的图为 $G'$。显然,我们选择 $G'$ 最小割的割边。
但是还有可能 $x$ 不够大,只有 $k$ 条边被扩大了($k <$ 最小割)。这种情况,我们需要将最短的若干条路径上的边扩大。发现这就是我们在 $G'$ 上,把 $w$ 当作费用,增广 $k$ 次的结果。
最后我们取 $\min{\frac {cost_i+x}{i}}$ 即可,这是可以由凸包推得的。
好吧,说得很扯淡,有能力的还是用线性规划推吧。。。
# [1299D Around the World](https://codeforces.com/problemset/problem/1299/D)
给定一张无向联通图,保证不存在一个长度 $\geq 3$ 的简单环经过了 $1$ 号点。
你需要求解,有多少种方案删除若干条与 $1$ 号节点相连的边,使得不存在任意一条路径(不一定是简单路径)满足其以 $1$ 号节点为起点,$1$ 号节点为终点,经过的所有边的边权异或和为 $0$,且至少经过了一条边奇数次。
$n,m\le 10^5,w\le 31$。
***
[评测链接](https://codeforces.com/contest/1299/submission/70706487)
思路并不难,主要还是考察代码整合的能力。
详见[题解](https://www.luogu.com.cn/blog/sysjuruo/solution-cf1299d)。
# [1286D LCC](https://codeforces.com/problemset/problem/1286/D)
一条无限长的管道中有 $n$ 个粒子,第 $i$ 个粒子的位置为 $x_i$,保证对于 $1\leq i <n$,有 $x_i<x_{i+1}$。
一次实验开始时,第 $i$ 个粒子会获得 $v_i$ 的初速度,并有 $\frac{p_i}{100}$ 的概率向右移动,$1-\frac{p_i}{100}$ 的概率向左移动。
当任意两个粒子移动到相同位置的时候,我们称之为一次碰撞。一次实验耗费的时间为所有碰撞发生时间的**最小值**。特别地,如果没有发生任何碰撞,我们认为这次实验耗费的时间为 $0$。
求一次实验期望耗费的时间。
***
[评测链接](https://codeforces.com/contest/1286/submission/101944578)
第一次碰撞肯定是相邻的两个粒子。
我们枚举第一次碰撞的是哪一对,以及它们俩的方向分别是什么。那么其他所有点的碰撞时间不能小于它。
设 $f_{i, 0/1}$ 表示前 $i$ 个粒子,第 $i$ 个方向是左 / 右,满足条件的概率,遇到枚举的点就钦定只有一个方向有值。
发现转移式可以写成矩阵。
每个点矩阵根据我们对碰撞时间的限制有三种(不存在合法情况,同向合法,同向和正向合法),还有一种表示被钦定。
我们按照碰撞时间从小到大枚举,每次修改当前位置的矩阵值为被钦定的矩阵,再修改状态改变了的点。
线段树维护矩阵即可。
# [1276F Asterisk Substrings](https://codeforces.com/problemset/problem/1276/F)
给定一个字符集为小写字母的长度为 $n$ 的字符串 $s$,设 $t_i$ 表示将 $s$ 中的第 $i$ 个字符替换为特殊字符 $\text{*}$ 时得到的字符串,比如当 $s=\text{abc}$ 时,$t_1=\text{*bc}$,$t_2 = \text{a*c}$,$t_3 = \text{ab*}$。
求字符串集合$\{s,t_1,t_2,t_3,...,t_n\}$中本质不同的子串个数(需要计算空串)。
***
[评测链接](https://codeforces.com/contest/1276/submission/101617200)
$S, S*, *S$ 都是很平凡的,主要问题在于计算形如 $S*T$ 的串的个数。
我们建立后缀自动机,对于 $\textrm{Right}$ 集合相同的 $S$ ,其对应的 $T$ 的数量是相同的。
一个串若干个后缀本质不同的前缀个数是很容易计算的。我们建立反串的后缀自动机,若这若干个后缀对应的结点按照后缀树的 $\textrm{dfs}$ 序排序后为 ${p_1, p_2, \ldots, p_k}$,则本质不同的前缀个数为 $\sum_{i=1}^k\textrm{len}(p_i)-\sum_{i=1}^{k-1}\textrm{len}(\textrm{lca}(p_i, p_{i+1}))$。
我们在正串的后缀自动机上,set 启发式合并反串结点即可。
时间复杂度:$O(n\log^2 n)$。
# [1270H Number of Components](http://codeforces.com/problemset/problem/1270/H)
给一个长度为 $n$ 的数组 $a$,$a$ 中的元素两两不同。
对于每个数对 $(i,j)$($i<j$),若 $a_i<a_j$,则让 $i$ 向 $j$ 连一条边。求图中连通块个数。
支持 $q$ 次修改数组某个位置的值,每次修改后输出图中连通块个数。
$n,q\le 5\times 10^5,1\le a_i\le 10^6$,保证任意时刻数组中元素两两不同。
***
[评测链接](https://codeforces.com/contest/1270/submission/83489866)
若 $i, j$ 在同一个连通块里,$i < x < j$,则 $x$ 也在这个连通块里。
所以每个连通块在原序列上是一个区间。$i$ 是分隔点当且仅当 $\min_{j \leq i}a_j>\max_{j > i}{a_j}$ 。
也就是说,我们需要计算 $v$ ($v$ 在序列中出现过)的数量,满足序列的一个前缀 $\geq v$,其余 $< v$。
设 $f_v$ 表示序列中 $i$ 的数量,满足 $a_i \geq v$,$a_{i+1} < v$。
那么 $f_v=1$ 的 $v$ 的数量就是答案。
发现修改会使得 $f$ 区间加减 $1$,查询全局最小值的个数。
线段树维护即可。
# [1267G Game Relics](https://codeforces.com/problemset/problem/1267/G)
现在有 $n$ 种圣物,其中第 $i$ 个圣物的价格为 $c_i$ 碎片。你想把这 $n$ 种圣物全买一遍,其中有两种购买方式:
- 花费 $c_i$ 碎片购买第 $i$ 种圣物。
- 花费 $x$ 碎片进行抽奖,可以等概率随机获得这 $n$ 种圣物中的一种,如果获得了已经获得过的圣物,则会还给你 $\frac{x}{2}$ 碎片。
现在求最优策略下,得到这 $n$ 种圣物的最小期望花费。
$n \leq 100$。
***
[评测链接](https://codeforces.com/contest/1267/submission/99017542)
我们一定是先若干张抽卡,然后再全买。因为抽卡的效率越来越低。
若现在还剩 $k$ 张卡,则以第二种方式获得一张卡的期望代价为 $(\frac nk-1)\frac x2+x$。
由于获得的卡是随机的,所以 $\sum c$ 期望减少 $\frac {\sum c}k$。
所以当 $k, \sum c$ 固定时,减少 $\sum c$ 有两种方案:
1. 效率为 $1$。
2. 效率为 $\frac {(\frac nk-1)\frac x2+x}{\frac{\sum c}{k}}$。
(效率 $= E(\frac{减少量}{代价})$)
取两者较大值更优。
所以我们设 $f_{i, j, k}$ 表示前 $i$ 种卡,剩 $j$ 张,$\sum c = k$ 的方案数。
把每种情况出现的概率乘上较优的效率求和即为答案。
时间复杂度:$O(n^2\sum c)$。
# [1239E Turtle](https://codeforces.com/problemset/problem/1239/E)
一只乌龟从 $2 \times n$ 的棋盘的左上角走到右下角,只能往下或往右,需要给出一种方案来分配 $2n$ 个数字使得乌龟走过的路径上的数之和的最大值最小。
$n \leq 25$,$a \leq 5\times 10^4$。
***
[评测链接](https://codeforces.com/contest/1239/submission/97041068)
首先,我们走的路径一定是第一行的一个前缀和第二行的一个后缀。所以我们应让第一行不降,第二行不升。
设第一行的数为 $a$,第二行的数为 $b$。则答案为 $\max_{i=1}^n\{\sum_{j\leq i}a_j+\sum_{j \geq i}b_j\}$。
设 $w_i=a_i-b_{i-1}$。则答案为 $a_1+\sum b+\max_{i=1}^n\sum_{j \leq i}w_j$。
发现 $w$ 是不降的,所以我们只用保留 $a_1 + \sum b$ 和 $\sum a + b_n$ 两条路径,其他的路径肯定不会比它们俩同时大。
而 $a_1, b_n$ 是必经点,我们把最小的两个元素给它们肯定更优。
问题变为:给定 $2(n-1)$ 个数,分成两个长度为 $n-1$ 的序列,使得 $\max(\sum a_i, \sum b_i)$ 尽可能小。
我们设 $f_{i, j, k}$ 表示是否存在一种方案使得前 $i$ 个数,第一个序列分了 $j$ 个,和为 $k$。背包转移即可。
甚至,你可以用 $\textrm{bitset}$ 优化。
时间复杂度:$O(n^2\sum a)$,$O(\frac 1\omega n^2\sum a)$。
# [1188D Make Equal](https://codeforces.com/problemset/problem/1188/D)
给出 $ n $ 个数字 $ a_1 , a_2 , \ldots , a_n $ ,每次操作可以给其中一个数加上 $ 2 $ 的非负整数次幂。求最少的操作次数,使得这 $ n $ 个数相等。
***
[评测链接](https://codeforces.com/contest/1188/submission/91697385)
我们把 $a$ 排序,问题转化为:寻找一个 $x$,使得 $\sum \textrm{popcnt}(x+a_n-a_i)$ 最小。
我们令 $a_i\leftarrow a_n-a_i$。
发现此题实际上和 [778E Selling Numbers](https://codeforces.com/problemset/problem/778/E) 是同一题。
我们设 $f_{i, S}$ 表示前 $i$ 位,向第 $i+1$ 位进位的集合为 $S$,最小花费是多少。这样的复杂度是 $2^n\log a$ 的。
我们发现,$S$ 可能的状态只有 $n+1$ 种。这是因为我们令 $b_i=a_i$ 的前 $i$ 位,则这个数进位需要 $2^i-b_i$,所以我们把 $b$ 排序,进位的只可能是一个后缀。
时间复杂度:$O(n\log n \log a)$。
可以用基数排序去掉 $\log n$。
# [1178H Stock Exchange](https://codeforces.com/problemset/problem/1178/H)
股票交易所里有 $2n$ 种股票,每种股票有两个属性 $a_i,b_i$,在时刻 $t\ge 0$,第 $i$ 种股票的价格为 $a_i*\lfloor t\rfloor+b_i$。
每个时刻可以进行任意次股票交易,在时刻 $t$ 时能够把股票 $i$ 换成股票 $j$ 当且仅当股票 $i$ 在时刻 $t$ 的价格不小于股票 $j$ 在时刻 $t$ 的价格。
现在你手上有 $1$ 到 $n$ 号股票各一张,现在要求的是把这些股票换成 $n+1$ 到 $2n$ 号股票各一张的最早时刻,以及在最早换完股票前提下的最少交易次数。
$1\le n\le 2200,0\le a_i,b_i\le 10^9$。
***
[评测链接](https://codeforces.com/contest/1188/submission/91697385)
我们显然可以发现,$T$ 有可二分性。
接下来有一个重要的结论:若 $T$ 是一个可行的答案,那么一定存在一种交换方案,使得仅在 $0$ 和 $T$ 这两个时间点进行交换。
我们考虑一组交换 $(a, b, t)$,若 $t$ 在 $a, b$ 交点左侧,则令 $t = 0$,否则令 $t = T$,如果没有交点,两边都行。
那么如何求出交换花费最少的次数呢?我们发现若把最初的股票和最后的股票连接,这就是一个类似于二分图匹配的问题。区别在于,我们可以换位置。于是我们建立网络流模型,在二分图匹配的基础上,左边的两个位置 $i, j$,$b$ 更大的往小的连边,右边的同理,$kt+b$ 更大的往更小的连边。
这样我们的边数是 $O(n^2)$ 的,无法接受,不过优化这样的连边是基本套路(前缀和优化建图),在此不再赘述。
不过由于网络流的复杂度较高(一种实现的方法是 $O(n^2)$),这样还是无法通过。而我们发现,二分只用判断其合法性,不用求出具体花费。于是我们可以不顾及花费,让每个左边的位置都换为 $b$ 比自己小的且 $kt+b$ 最大的股票,之后我们再贪心地从大往小判断能否匹配。这样的复杂度是 $O(n\log n)$ 的,可以通过。
# [1178G The Awesomest Vertex](https://codeforces.com/problemset/problem/1178/G)
给定一棵根为 $1$ 的有根树,每个节点有两个权值 $a[i]$ 和 $b[i]$ 。定义 $R(v)$ 为 $v$ 祖先的集合(包括自己),则一个节点 $v$ 有多棒取决于其好的程度,好的程度是这样定义的:
$$ \left| \sum_{w \in R(v)} a_w \right| \cdot \left| \sum_{w \in R(v)} b_w \right|$$
现在需要支持两种操作:
- $1 \ \ v \ \ x$ — 将 $a_v$ 加上 $x$。
- $2 \ \ v$ — 输出以 $v$ 为根的子树中最大的好的程度。
$1≤n≤2⋅10^5$,$1≤q≤10^5$,$ 1\leq x \leq 5000 $。
***
[评测链接](https://codeforces.com/contest/1178/submission/106745768)
$\left| \sum_{w \in R(v)} b_w \right|$,最初的 $\left| \sum_{w \in R(v)} a_w \right|$ 显然是可以直接求出来的。
之后,我们把操作 $1$ 看作子树操作,好的程度定义为 $\max_{w \in R(v)}\left |a_wb_w\right |$。
这样,我们就只有子树操作了,用 $\textrm{dfs}$ 序转化为序列问题。
问题变为:区间加正数,区间求 $\max_{w \in R(v)}\left |a_wb_w\right |$。$|a_wb_w|=\max(a_wb_w, -a_wb_w)$。
$\textrm{KTT}$ 即可。
当然,我是不会的,所以我用了分块。
我们对于每个块维护所有 $b_wx + a_wb_w$ 构成的的凸包,整块加的时候,二分出最优的位置。由于加的是正数,我们只用维护一个指针,每次向后移。
零散块重建整个凸包。
时间复杂度:$O(n\log^2n)$,$O(n \sqrt n)$。
# [1175G Yet Another Partiton Problem](https://codeforces.com/problemset/problem/1175/G)
给定数组 $a_1,a_2\cdots a_n$,你需要将它划分成 $k$ 段(每个元素在且仅在一段中),某段 $a_l,a_{l+1}\cdots a_r$ 的权值为 $(r-l+1)\times \max_{l\leq i\leq r}\{a_i\}$,整个划分的权值是每段权值之和。求最小划分权值。
***
[评测链接](https://codeforces.com/contest/1175/submission/94838735)
好题。
设 $f_{i, l}$ 表示前 $i$ 个点,划分成了 $l$ 段的最小权值。则有:
$$f_{i, l}=\min\{f_{j, l-1}+(i-j+1)\max_{j \leq p \leq i} a_p\}$$
我们考虑按第二维分层计算,假设我们已经算出了 $f_{1, l-1}, f_{2, l-1}, \ldots, f_{n, l-1}$。
我们用单调栈把序列化成若干段,每段的 $\max$ 相同。
每段中,我们需要求出 $f_{j, l-1}-j\times \max$ 的最小值,可以斜率优化,维护凸包。
单调栈可能会合并凸包,由于两个凸包的斜率是不交的,我们用启发式合并。
每个凸包求出一个结果 $b$,我们需要求出所有的 $\max \times x + b$ 在 $x=i$ 处的最小值,并且还需要支持撤销(由于合并凸包要删除一条直线),所以我们不能再用均摊复杂度的凸包了,只能用严格复杂度的李超树。
时间复杂度:$O(nk\log n)$。
# [1172F Nauuo and Bug](https://codeforces.com/problemset/problem/1172/F)
现在给定数组 $a$ 和 $p$,要求多次询问 $\textrm{sum}(a, l, r, p)$ 的值。
$\textrm{sum}(a, l, r, p)$ 的定义为,从 $l$ 到 $r$,如果 $\textrm{result}+a_i\geq p$,$\textrm{result} \leftarrow \textrm{result} + a_i - p$,否则 $\textrm{result} \leftarrow \textrm{result} + a_i$。
***
[评测链接](https://codeforces.com/contest/1172/submission/93169442)
不太会,咕了。
# [1168D Anagram Paths](https://codeforces.com/problemset/problem/1168/D)
给出一个有根二叉树,每一条边上都有一个小写字母或 `?`。
称一个根到叶子的路径上的字母组成的字符串和这个叶子**相关联**。如果有一种方案把每个问号换成一个小写字母,使得所有叶子关联的字符串两两之间互相是对方的**重新排列**,那么称这棵树是**可重排的**。
如果一棵树是**可重排的**,那么某个字母 ``c`` 的**重排度** $f(c)$ 定义为在所有使树重排的问号赋值方案中,``c`` 在任何一个关联串中出现次数的最大值。
如果设 $id(c)$ 是字母 $c$ 的标号,即 $id(\texttt{'a'})=1,id(\texttt{'b'})=2$……,那么整棵树的**重排度**是
$$\sum_{c}f(c)id(c)$$
给出 $Q$ 次操作,每次操作替换一条边上的字符,求操作后,树是否**可重排**。如果**可重排**,输出它的**重排度**。
***
[评测链接](https://codeforces.com/contest/1168/submission/95963984)
首先,很显然地,叶子的深度必须相同。
在这个条件下,有解当且仅当
$$\forall u, \sum_{i=0}^{c} \text{maxi}_{u, i}\leq d-\text{dep}_u $$
其中,$\text{maxi}_{u, i}$ 表示以 $u$ 号点为起点向下的所有链中,第 $i$ 种字符最多为多少。$c$ 为字符集大小,$d$ 为叶子深度,$\text{dep}_u$ 为 $u$ 号点的深度。
必要性是显然的。
充分性可以考虑,我们假如让每一个子树都已经满足了条件,那么就可以把子树看作一条链(因为集合与个数都是一样的),这样我们考虑 $u$ 子树的时候,只用考虑两条在 $u$ 分叉的链如何解决。这个问题就非常简单了。除此之外,我们还得到了一条结论:最终答案中的一部分应该是 $(d-\sum \text{maxi}_{1, i})(1+2+\ldots +26)$。
现在,我们考虑修改该怎么处理。
我们思考,若一条边修改了权值,那么他的祖先们的 $\text{maxi}$ 值应该修改,其他点不需要修改。
我们可以用动态 dp 解决这个问题。
当然,有更容易的做法。
我们发现,假如树的一个部分形如一条链,其实我们可以把链缩成一条边,之后每次 $O(c)$ 计算。
也就是说,我们现在把原树变成了包含所有叶子的虚树。
有结论:此时的树高不会超过 $O(\sqrt n)$。
我们考虑在虚树上一条长为 $l$ 的链,要满足虚树的性质,就必须要在每个节点再深出一条枝干,又因为要求所有叶子的深度相同,所以枝干长度必须足够长。最终,我们需要 $O(l^2)$ 个点才能使这样一条虚树上的链存在。
于是我们建出虚树,在这个虚树上暴跳,维护 $\text{maxi}$ 值即可。
时间复杂度:$O(cn\sqrt n)$。
# [1163F Indecisive Taxi Fee](https://codeforces.com/problemset/problem/1163/F)
给你一个 $n$ 个点,$m$ 条边的无向图,每条边连接点 $u, v$,长度 $w$。
有 $q$ 次询问,每次询问给你一对 $t, x$,表示仅当前询问下,将 $t$ 这条边的长度修改为 $x$,请你输出当前 $1$ 到 $n$ 的最短路长度。
$n, m, q \leq 2\times 10^5$。
***
[评测链接](https://codeforces.com/contest/1163/submission/92954550)
若 $(u, v)$ 不在最短路上,容易解决。
若 $(u, v)$ 在最短路上且边权变小了,容易解决。
若 $(u, v)$ 在最短路上且边权变大了,是我们要处理的关键。
我们求出最短路树。有可能的答案是原路,或者走过一条非树边,跨过 $(u, v)$。
则一条非树边 $(u', v')$ 路径上的某条边被修改后,有可能的答案为 $(u', v')$。
所以 $\textrm{dis}(1, u')+(u', v')+\textrm{dis}(v', n)$ 或者 $\textrm{dis}(1, v')+(u', v')+\textrm{dis}(u', n)$ 给 $(u', v')$ 上的边做贡献。
由于所有的操作先于询问,我们可以用“倍缩”(倍增,但贡献方向全部反向,即 $f_{u, i} \to f_{u, i-1}/f_{\textrm{anc}_{u, i-1}, i-1}$)完成。
# [1149D Abandoning Roads](https://codeforces.com/problemset/problem/1149/D)
一张 $n$ 个点 $m$ 条边的无向图,只有 $a,b$ 两种边权($a <b$),对于每个 $i$,求图中所有的最小生成树中,从 $1$ 到 $i$ 距离的最小值。
$n \leq 70$,$m \leq 200$。
***
[评测链接](https://codeforces.com/contest/1149/submission/100607839)
对于一个最小生成树,我们把 $b$ 边删去,剩下了若干连通块,则所有不同的最小生成树一定是这些连通块之间的任意一棵生成树,每个连通块内的任意一棵生成树。
考虑什么情况下会使得较短的路径不合法呢?连通块内由于任意一棵生成树都合法,所以在连通块内的简单路径都是合法的,连通块之间的任意一棵生成树都是合法的,所以把连通块看作一个点,所有的简单路径都是合法的。
问题就出在后者的简单路径上。下图就是一个不满足条件的情况。
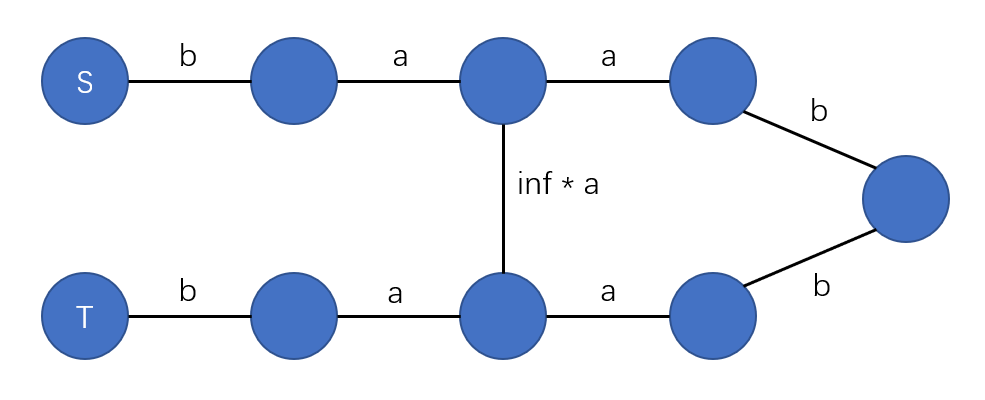
从最短路的角度,我们走了右侧的点,但在最小生成树的角度上,我们并不能走。
所以我们应该着力于保证简单路径。可以把所有的连通块状压,这样的状态数是 $2^n$ 的。但是我们发现,若连通块大小 $\leq 3$,我们肯定不会走两遍,这样会走重复的点,肯定不优。所以只用考虑 $\geq 4$ 的连通块即可。
时间复杂度:$O(2^{\frac n4}m)$。
# [1142E Pink Floyd](https://codeforces.com/problemset/problem/1142/E)
给定一张 $n$ 个点的竞赛图。边分为粉色和绿色。粉色的边有 $m$ 条,你已经知道了它们的方向。而绿色的边你不知道方向。
每次询问,你可以获得一条绿色的边的方向。
你需要在 $2n$ 次询问内,找到一个点 $u$,使得对于每个点 $v$,都有一条 $u\to v$ 的路径,使得路径上每条边同色。需要注意的是路径只能通过粉边和你已经询问的绿边。
交互库是自适应的。
$n, m \leq 10^5$。
***
[评测链接](https://codeforces.com/contest/1142/submission/101926229)
如果没有粉色边,我们可以这样构造:每次选出两个可能为答案的点,询问两者之间的边的方向,如果是 $(u, v)$,则钦定 $v$ 不为答案,直至剩余一个点,就是答案。
所有“钦定不为答案”的 $v$ 构成的集合也可以这么看:所有可能为答案的点都能够到达的点的集合,或者说已经处理完的点的集合。
回到原题,上面的询问可能会因为 $(u, v)$ 已经有粉色边而失败。怎么办呢?我们考虑若粉边连成了一个无环图,可以每次选出入度为 $0$ 的点作为已经可能是答案的集合,而不为 $0$ 的为已经处理完的集合。若度数为 $0$ 的点只剩 $1$ 个,它就是答案。因为它能够通过粉边到达所有未处理的节点,通过绿边到达已经处理的节点。
需要注意的是我们钦定 $v$ 不是答案的时候,需要立刻把它的后继中度数为 $0$ 的放入集合中。
# [1097G Vladislav and a Great Legend](https://codeforces.com/problemset/problem/1097/G)
给定一棵有 $n$ 个节点的树 $T$。
$f(X)$ 是点集 $X$ 的虚树的大小。求
$$\sum_{X\subseteq\{1,2,\dots,n\},X\neq\varnothing}(f(X))^k$$
$n \leq 10^5$,$k \leq 200$。
***
[评测链接](https://codeforces.com/contest/1097/submission/95630005)
$$f(X)^k=\sum_{i=0}^k \binom{f(X)}{i} {k \brace i}$$
所以我们要求 $\sum\binom{f(X)}{i}
考虑组合意义,就是要我们在虚树中选出 i 个特殊点。
设 f_{u, i} 表示 u 号点,所在的虚树已经选了 i 个点的贡献和,树上背包即可。
根据树背包的 trick,时间复杂度为:O(nk) 。
1097E Egor and an RPG game
设 f(n) 表示满足所有长度为 n 的排列都能被划分成 k 个不相交的单调上升/单调下降子序列的 k 的最小值。
多组数据,给定长为 n 的排列,输出一种单调序列个数不超过 f(n) 的划分方案。
最少的上升子序列的划分次数=最长下降子序列的长度
若前者 \geq \sqrt n ,我们用后者,否则用前者,这样保证我们只用 \sqrt n 次就能划分完成。
# [1091G New Year and the Factorisation Collaboration](https://codeforces.com/problemset/problem/1091/G)
给定 $n$($21\leq n \leq 2^{1024}$),求 $n$ 的质因数。保证 $n$ 的所有质因数均为 $4x+3$ ($x$ 为自然数)的形式且至多由 $10$ 个质因数相乘得到。
IO 交互提供了高精度计算。
`+ x y` 给定 $x, y$($0\leq x < n$),返回 $(x+y)\bmod n$。
`- x y` 给定 $x, y$($0\leq x < n$),返回 $(x-y)\bmod n$。
`* x y` 给定 $x, y$($0\leq x < n$),返回 $(x\cdot y)\bmod n$。
`/ x y` 给定 $x, y$($0\leq x < n$),返回 $(x\cdot y^{-1})\bmod n$。假如 $y, n$ 不互质,返回 `-1`。
`sqrt x` 给定 $x$($0\leq x < n$),返回 $y$($0\leq y < n$)满足 $y^2\bmod n=x$,若不存在返回 `-1`。
`^ x y` 给定 $x, y$($0\leq x < n$),返回 $(x^y)\bmod n$。
你至多可以使用 $100$ 次交互库。运算花费时间表如下:
`+ x y` 至多 1 ms。
`- x y` — 至多 1 ms。
`* x y` — 至多 1 ms。
`/ x y` — 至多 350 ms。
`sqrt x` — 至多 80 ms。
`^ x y` — 至多 350 ms。
***
[评测链接](https://codeforces.com/contest/1091/submission/96978106)
交互本质有何用?
我们仔细思考,加减乘除乘方我们都能直接实现,唯独 `sqrt` 似乎不好实现。
我们设 $n = p_1p_2\ldots p_k$。
我们考虑如何通过 `sqrt` 获取信息。设 $y=x^2$,我们询问 `sqrt y` 得到了一个不同于 $x$ 的解 $x'$,那么
$$x^2=x'^2 \pmod n$$
$$(x-x')(x+x')=0 \pmod n$$
$$(x-x')(x+x')=kn$$
那么 $x-x'$ 和 $x+x'$ 将 $n$ 的质因数分成了两个集合 $S_1, S_2$。
我们进行若干次这样的操作,得到了若干个 $S$,那么我们能求出一个质因子 $p_i$ 当且仅当对于每个 $j\neq i$,存在一个 $S$ 使得 $p_j$ 在 $S$ 中出现但 $p_i$ 没有出现。
那么我们如何得到一个 $x'$?
我们把第一个式子展开:
$$x^2-x'^2=0 \pmod {p_1}$$
$$x^2-x'^2=0 \pmod {p_2}$$
$$x^2-x'^2=0 \pmod {p_3}$$
$$\ldots$$
这些式子中只要有一个成立,最后我们用 CRT 合并回去就是原式。
$x^2-x'^2=0 \pmod {p}$ 的解为 $x'=x$ 和 $x = p-x$。
也就是说我们共有 $2^k$ 种解,无论交互库如何进行,我们的 $x$ 对方是不知道的,所以返回的 $x'=x$ 的概率是 $2^{-k}$,显然,这个概率很小。
并且由此我们得到:$S_1, S_2$ 的分配也是随机的。所以 $p_i, p_j$ 不同时出现在一个 $S$ 中的概率为 $50\%$。
我们随机找到 $t$ 组 $S_1, S_2$,这样对一个 $i$,一个 $j$ 满足的概率为 $1-2^{-t}$,全部 $(i, j)$ 都满足的概率为 $(1-2^{-t})^{k^2}$。
令 $t=50$,则正确性已经足够。
由于要使用高精度,代码使用 python,不过十分简单。
loj563 也是这 trick。
# [1083D The Fair Nut's getting crazy](http://codeforces.com/problemset/problem/1083/D)
给定一个长度为 $n$ 的序列 $\{a_i\}$。你需要从该序列中选出两个非空的子段,这两个子段满足:
- 两个子段非包含关系。
- 两个子段存在交。
- 位于两个子段交中的元素在每个子段中只能出现一次。
求共有多少种不同的子段选择方案。输出总方案数对 $10^9 + 7$ 取模后的结果。
需要注意的是,选择子段 $[a, b]$、$[c, d]$ 与选择子段 $[c, d]$、$[a, b]$ 被视为是相同的两种方案。
$1 \leq n \leq 10^5, -10^9 \leq a_i \leq 10^9$。
***
[评测链接](https://codeforces.com/contest/1083/submission/117481782)
考虑 $[l, r]$ 作为交集能产生的贡献。
设 $\textrm{las}_i$ 表示等于 $a_i$ 的元素在 $i$ 之前最后一次出现的位置 + 1,$\textrm{nxt}_i$ 表示在 $i$ 之后的第一次 - 1。
那么 $[l, r]$ 能够覆盖到的位置应该是 $[\max\{\textrm{las}_i\}, \min\{\textrm{nxt}_i\}]$,贡献为 $(l-\max\{\textrm{las}_i\})(\min\{\textrm{nxt}_i\}-r)$。
注意如果 $\max\{\textrm{las}_i\} \geq l$ 或者 $\min\{\textrm{nxt}_i\}\leq r$,那么贡献为 $0$。
拆开得 $l\min\{\textrm{nxt}_i\}+r\max\{\textrm{las}_i\}-\max\{\textrm{las}_i\}\min\{\textrm{nxt}_i\}-lr$。
考虑从大到小枚举 $l$,维护每个 $r$ 的答案。
设 $a, b$ 为两个数组,维护 $\max\{\textrm{las}_i\}$ 和 $\min\{\textrm{nxt}_i\}$。
那么 $i$ 左移的时候我们需要完成以下操作:
* $a$ 区间取 $\max$。
* $b$ 区间取 $\min$。
* 区间 $a_ib_i$ 求和。
* 区间 $b_i$ 求和。
* 区间 $ia_i$ 求和。
由于 $a, b$ 数组都是单调的,线段树维护即可。
# [1067D Computer Game](http://codeforces.com/problemset/problem/1067/D)
有 $n$ 个游戏,每个游戏有收益 $a_i$,升级后的收益 $b_i$,每次成功概率 $p_i$。每秒可以玩一个游戏,如果成功则得到当前收益,并且可以升级任意某个游戏。求 $t$ 秒后的期望收益的最大值。
$n\leq 10^5$,$t\leq 10^{10}$,$a_i<b_i$。
***
[评测链接](https://codeforces.com/contest/1067/submission/102094366)
我们获得了一次升级的机会后,便可以一直选择期望收益最大的游戏,设其期望为 $M$。
问题在于,没有升级的时候,我是选择一个期望收益高的,还是升级快的?
我们设 $f_i$ 表示剩下 $i$ 个时刻,还没有升级的最大的期望收益。
$$f_i=\max_j\{(1-p_j)f_{i-1}+p_j(M(i-1)+a_j)\}$$
$$f_i=f_{i-1}+\max_j\{p_j(M(i-1)-f_{i-1})+p_ja_j\}$$
我们把 $p_jx+p_ja_j$ 构成的凸包求出。
又发现,$Mi-f_i$ 是单调的,因为 $M$ 是 $b$ 中期望最大的,肯定比 $a$ 中的大。
所以用指针扫过去即可做到 $O(t)$。
又发现,在同一个决策的一段的转移是线性关系。矩阵优化,二分找到下一个决策点,这样是两只 $\log$ 的。不过多次矩阵乘我们有套路:预处理矩阵的 $2$ 的幂,倍增即可。
时间复杂度:$O(n \log t)$。
# [1037H Security](https://codeforces.com/problemset/problem/1037/H)
给出一个字符串 $S$。
给出 $Q$ 个操作,给出 $L, R, T$,求字典序最小的 $S_1$,使得 $S_1$ 为 $S[L\ldots R]$ 的子串,且 $S_1$ 的字典序严格大于 $T$。
$1 \leq |S| \leq 10 ^ 5, 1 \leq Q \leq 2 \times 10 ^ 5, \sum |T| \leq 2 \times 10 ^ 5$。
***
[评测链接](https://codeforces.com/contest/1037/submission/88109028)
考虑 $T$ 在 $S$ 的后缀自动机上匹配一段,之后拼接一个比它大的字符,如果不存在,就减小匹配长度。如何确定是否存在呢?线段树合并。
# [1034E Little C Loves 3 III](https://codeforces.com/problemset/problem/1034/E)
给定集合幂级数 $a, b$,求子集卷积 $\bmod 4$ 的结果。
$n \leq 2^{21}$。
***
[评测链接](https://codeforces.com/contest/1034/submission/74563138)
子集卷积的占位多项式限制了 $\textrm{popcnt}(a)+\textrm{popcnt}(b)=\textrm{popcnt}(c)$。我们也可以理解为满足 $p^{a+b-c}\mod p=1$ 的 $c$。
也就是说,我们可以把占位多项式理解为一个分离了 $p$ 的次数的高精度。
在这个题中,$p$ 很小,根本不需要高精度,所以直接 $a_i\leftarrow a_i\times 4^{\textrm{popcnt}(i)}$ 做 FWT 就好了。
# [1019C Sergey's problem](https://codeforces.com/problemset/problem/1019/C)
给定一张无向图,你需要选出一个独立集,使得不在集合的点都能够通过某个集合里的点经过至多 $2$ 步到达。
$n, m \leq 10^6$。
***
[评测链接](https://codeforces.com/contest/1019/submission/91620832)
奇怪的题。
先考虑满足第二个性质。显然我们能够构造出一个集合使得至多 $1$ 步到达。比如我们从大到小枚举,如果一个点没有被标记,那么把它选入,并把它能到达的点打上标记。
这样会造成有 $x > y, x \to y$ 的情况。考虑从大到小,如果一个点被选了,就把它能到达的点删去。这样,我们把选入的点染成白色和黑色,黑色是最终选的,白色是被删去的,那么白色、黑色都构成了独立集。所以我们不会从白色走到白色。所以至多 $2$ 步就能到达。
# [1012E Cycle sort](https://codeforces.com/contest/1012/submission/97993166)
给定一个长为 $n$ 的数组 $a$。
你可以进行若干次操作。每次操作给出 $k$ 的不同的下标 $i_1, i_2, \ldots, i_k$,然后将这些下标的元素进行顺时针轮换。即:$a_1\to a'_2, a_2\to a'_3, \ldots, a_{k-1}\to a'_k, a_k \to a'_1$。
现在要求所有操作的 $k$ 的总和不超过 $s$ 的前提下,将 $a$ 数组排序的操作数的最小值。无解输出 `-1`。
$n, s \leq 2 \times 10^5$。
***
[评测链接](https://codeforces.com/contest/1012/submission/97993166)
假设元素互不相同,我们考虑每个位置指向它最终所在的位置。这样构成了若干个环。
如果环数 $\geq 2$,我们可以通过两轮操作完成:
1. $(a_1, a_2, \ldots, a_{k_1}, b_1, b_2, \ldots, b_{k_2}, c_1, c_2, \ldots, c_{k_3}\ldots )
(z_1, y_1, \ldots, c_1, b_1, a_1)
这样的操作总数是 n+c 的,c 是环的个数。
如果 s < n+c ,我们只能把一些环自我处理。
如果有两个环相同的数,那么我们可以交换他们俩的出边,使两个环变成一个环。这个可以用并查集处理。处理完后,每两个环的数的集合不交,肯定不可能再变成一个环了。
1007D Ants
有一棵树有 n 个顶点。还有 m 只蚂蚁住在上面。每只蚂蚁都有自己的颜色。第 i 只蚂蚁有两个最喜欢的顶点对:(a_i, b_i) 和 (c_i, d_i) 。
你需要知道是否可以用 m 种颜色绘制树的边,以便每个蚂蚁能在其最喜欢的一对顶点对之间行走且这条边的颜色与这只蚂蚁相同。如果可能,你需要输出每个蚂蚁行走的顶点对。
***
[评测链接](https://codeforces.com/contest/1007/submission/98349566)
暴力的做法是直接建图跑 2-SAT。
2-SAT 图中,$u \to v$ 表示若 $u$ 选了,那么 $v$ 也要选。
考虑在图中如何限制若干元素中只有至多一个被选。记第 $i$ 个元素为 $(a_i, b_i)$,$a_i$ 表示选了,$b_i$ 表示没选。$s_i$ 表示前 $i$ 个是否有元素被选。则 $a_i \to s_i, s_i \to b_{i+1}$。
对树进行树剖+线段树,线段树中,一个结点内只能选一个,所以我们对包含这个结点的所有元素进行上述操作。父亲和儿子之间也只能选一个。所以我们再把父亲的 $s_n$ 连向儿子的 $s_1$ 即可。
时间复杂度:$O(m \log^2 n)$。
# [986F Oppa Funcan Style Remastered](https://codeforces.com/problemset/problem/986/F)
给定 $n$ 与 $k$,问是否能将 $n$ 分为若干个 $k$ 的因数($1$ 除外)之和。
$n\leq 10^{18}$,$k\leq 10^{15}$,最多 $50$ 种不同的 $k$。
一共 $t$ 组询问,$t\leq 10^4$。
***
[评测链接](https://codeforces.com/contest/986/submission/98094895)
如果 $k$ 只有两个因数,跑 exgcd。否则同余最短路。
分解质因数的时候先预处理好质数,这样能除一个 $\log k$。
时间复杂度:$O(n+T(\frac {k^\frac 12}{\log k} + d(k)k^\frac 13\log k))$。
$d(k)$ 表示因数个数,$T$ 是不同的 $k$ 的个数。
# [986D Perfect Encoding](https://codeforces.com/problemset/problem/986/D)
给出 $n$,请选出 $m$ 个可以相同的正整数 $a_i$,使 $\prod_{i=1}^ma_i\ge n$,且 $\sum_{i=1}^ma_i$ 最小(不一定要最小化 $m$)。
***
[评测链接](https://codeforces.com/contest/986/submission/98028948)
根据相关理论,$n \to \infty$ 时,$a$ 应该取 $e$ 最优。
离 $e$ 最近的整数是 $3$,所以 $a$ 应该全是 $3$。
当然有几个特殊的情况,比如若干个 $3$ 带一个 $2$,带两个 $2$,这要根据和 $\bmod 3$ 的情况分类。
实现一个高精度即可。
但是这样复杂度爆炸,所以我们先估计一下,发现答案应该是 $\log_3 n+O(1)$,从 $\log_3 n$ 开始枚举即可。
# [963E Circles of Waiting](https://codeforces.com/problemset/problem/963/E)
在平面直角坐标系上,有一个神奇的点,一开始在 $(0, 0)$ 。每秒钟这个点都会随机移动:如果它在 $(x, y)$ ,下一秒它在 $(x - 1, y)$ 的概率是 $p_1$ ,在 $(x, y - 1)$ 的概率是 $p_2$ ,在 $(x + 1, y)$ 的概率是 $p_3$ ,在 $(x, y + 1)$ 的概率是 $p_4$ 。保证 $p_1 + p_2 + p_3 + p_4 = 1$ ,各次移动互不关联。
求出这个点移动至距离原点距离为大于 $R$ 的点的期望步数。距离为欧几里得距离。
$R \leq 50$。
***
[评测链接](https://codeforces.com/contest/963/submission/98167137)
列出式子,有 $O(R^2)$ 个变量,高斯消元是 $O(R^6)$ 的。
但是我们发现,与一个点相关的点最多和它差一行一列。如果我们从上到下,从左往右编号,那么第 $i$ 个等式第一个未知量是 $O(i)$ 的,结束位置是 $O(i+R)$ 的。高斯消元的后面两层循环就只用枚举 $O(R)$ 项。
时间复杂度:$O(R^4)$。
# [936E Iqea](https://codeforces.com/problemset/problem/936/E)
在无限的二维网格上,你需要维护两种操作。
1. 在 $(x, y)$ 处新开一个商店。
2. 询问离 $(x, y)$ 最近的商店的距离。
唯一能够通过的路径,是 $n$ 个给定的点,若两个点的位置四相邻,那么可以直接通过。保证这些长条连通且二维网格的剩余部分也连通。路径的长度定义为走过的网格数。
***
[评测链接](https://codeforces.com/contest/936/submission/97411056)
如果我们把一个长条缩成一个点,两个相邻的长条连边,那么根据题目性质,它构成了一棵树。
树上进行着两个操作是经典点分树题。
但是有一点小问题,长条是有长度的。
点 $x, y$ 走最短路到长条 $u$ 的 $a, b$ 两点,那么 $x, y$ 的距离为 $dis(x, a) + dis(y, b) + |a-b|$。
这个式子的处理又是一个经典题。我们从左往右扫,维护 $dis(x, a) - a$ 的最小值,和 $dis(y, b) + b$ 的和取最小值,这样考虑了 $b \geq a$ 的情况,再反着做一遍即可。
时间复杂度:$O(n\log^2 n)$。
# [908H New Year and Boolean Bridges](https://codeforces.com/problemset/problem/908/H)
设 $f(i,j)$ 表示 $i$ 是否能直接或间接到达 $j$。
给定一个 $n\times n$ 的矩阵 $G$,求满足以下条件的有向图的最小边数:
- 若 $G_{i,j}=\mathsf{A}$,则要求 $f(i,j) \operatorname{and} f(j,i)=1$。
- 若 $G_{i,j}=\mathsf{O}$,则要求 $f(i,j) \operatorname{or} f(j,i)=1$。
- 若 $G_{i,j}=\mathsf{X}$,则要求 $f(i,j) \operatorname{xor} f(j,i)=1$。
$n\leq 47$。
***
[评测链接](https://codeforces.com/contest/908/submission/92507337)
我们考虑,若 $(i, j)$ 的限制为 $A$,则 $(i, j)$ 肯定是强连通的。显然,若 $(i, j)$ 和 $(j, k)$ 的限制都为 $A$,则 $(i, k)$ 也是强连通的。
所以我们把他们看作一个个连通块。一个连通块 $E'$ 就是一个强连通分量。我们至少要用 $|E'|$ 条边使得他们强连通(比如,连一个大环)。
由于对于每一对点都有至少一个限制,所以连通块与连通块间还需要单向连通。
对于两个连通块 $E_1, E_2$ 之间,若存在限制 $X$,则 $E_1, E_2$ 必然为单向联通,若全为 $O$,则可以单向联通也可以强连通。
对于大小 $\geq 2$ 的连通块,单向联通花费($|E_1|+|E_2|+1$)比强连通花费更多。所以我们要考虑把尽可能多的单向联通转化为强连通。
而大小为 $1$ 的连通块,两种花费相同,也就没有了决策,直接把答案加上即可。
大小 $\geq 2$ 的连通块最多只有 $\frac n2$ 个。我们考虑状压,之后考虑每次将一个强连通分量加进去。
设 $f_S$ 表示 $S$ 中的元素是否能构成一整个强连通分量。
设全集为 $T$。
则这部分答案为 $\min\{k|[T]f^k\neq 0\}$,其中乘法为子集卷积。
即最小的 $k$ 满足 $T$ 能拆分成 $k$ 个部分 $\{S_1, S_2, \ldots, S_k\}$,使得 $f_{T} \neq 0$。
直接实现复杂度会非常高。
我们这时候发现,实际上并不需要用子集卷积。因为若 $S_1$ 和 $S_2$ 有交,也能说明 $S_1\cup S_2$ 能缩成两个强连通分量(有交实际上是更强的一个条件)。
我们又发现,我们只需要求 $f^k_{T}$ 的值,并不需要每次都 $\text{IFWT}$ 回来,只需要考虑每一个位置在 $\text{IFWT}$ 时对 $T$ 这个位置的贡献就好了,经过简单推导即可得到结论(结论见代码)。
时间复杂度:$O(n2^{\frac n2})$。
# [878E Numbers on the blackboard](https://codeforces.com/problemset/problem/878/E)
给出 $n$ 个数字,每次询问一个区间 $[l,r]$,对这个区间内部的点进行操作。每次操作可以合并相邻两个数 $x, y$ ,将它们变成 $x+2y$ 对于每次询问输出当最后只剩下一个数字时,这个数字的最大值。
询问互相独立。
$n, q \leq 10^5$。
***
[评测链接](https://codeforces.com/contest/878/submission/97536058)
考虑每个位置最后的权重 $a_i2^{k_i}$,不难发现 $k$ 有如下限制。
* $k_i \leq k_{i - 1} + 1
并且所有满足条件的 k 都能取到。这是因为我们考虑 i 和 i+1 在 i 已经合并了 k_{i-1}-k_i+1 次后把它们俩合并,就能得到这样的 k 序列。
那么,我们对这个问题的分析应该这样:
所以当我们遇到一个负数时,先把它单独放在外面,不要合并。假如它和后面的数合并后变成了正数,我们再把它与前面合并。
我们考虑模拟这个过程,用并查集实现。询问离线后,在右端点加入后考虑计算一段后缀和。维护每个块的后缀和即可。
时间复杂度:O(n\log n) 。
865E Hex Dyslexia
给定一个十六进制数,已知他是两个数 a, b 的差,且 a 在十六进制下的数位经过重新排列可以得到 b 的十六进制表示。
求最小的 b 。
输入长度 \leq 14 。
评测链接
我们设输入的数为 d ,d 在十六进制下的数位和 s 。
则 \frac s{15} 为 b+d 在十六进制下加法的进位次数。
后者等价于 a-b 的借位次数,最初 a 的数位和减 b 的数位和等于 0 。每借一次位,数位和多 15 ,所以两者相同。
知道了进位次数后,我们需要知道哪些位置进了位,这一步的复杂度至多是 \binom{13}{6}=1716 。
在知道了哪些位进位后,我们便可以知道每个 a_i-b_i 的值。
我们设置换为 p ,则我们知道了 a_i-a_{p^{-1}_i} 的值。
此时,每个环都有一个相同的元素,合并环的套路在这里再次得到了应用。
**为什么要合并成一个环呢?因为有多个环,还得考虑每个元素在哪个环里,这是很麻烦的。**
当所有的元素都在同一个环中,我们从一个 $0$ 开始,对所有合法的放置顺序取权值最小值。这一步可以通过状压 dp 解决。
我们设 $f_S$ 表示目前已经放的位置的集合为 $S$ 的 $b$ 的最小值。每次考虑一个新的位置,它的数值为 $a_{p_{\text{start}}}+\sum_{i\in S} a_{i}-a_{p^{-1}_i}$。如果数值在 $[0, 15]$,这就是合法的一步放置。
我们令 $p_{\text{start}}$ 为 $d$ 的最高位即可。这是因为 $b$ 的最高位始终为 $0$。考虑两种情况,若 $d$ 的最高位为 `f`,则 $b$ 只能为 $0$,若不为 `f`,则一种合法解 $\frac d{15}$ 的最高位为 $0$。
时间复杂度:$O(\binom{n}{\frac n2}n2^{n})$。
# [855G Harry Vs Voldemort](https://codeforces.com/problemset/problem/855/G)
假设一棵树有 $n$ 个节点和 $n-1$ 条边,在树的节点增加 $q$ 条新边。在每一次增加新边后,你需要告诉形如 $(u,v,w)$ 的三元组,使得 $u,v,w$ 都不相同,并存在两条路径:$u$ 到 $w$ 之间和 $v$ 到 $w$ 之间,使得两条路径没有共同边。
$n, q \leq 10^5$。
***
[评测链接](https://codeforces.com/contest/855/submission/91760663)
考虑三种情况,$u, v, w$ 在一个边双里,$u, v$ 有一个在 $w$ 的边双里,三个没有在同一个边双里。
瞎算算就好了。
# [848E Days of Floral Colours](http://codeforces.com/problemset/problem/848/E)
给定一个有 $2n$ 个点的环,有 $n$ 种颜色,每个点有一种颜色,每种颜色恰好有两个点,它们俩的距离要么 $\leq 2$,要么 $=n$,对于一种颜色序列,我们把距离 $=n$ 的点全部去掉,贡献为连续段长度的乘积。求所有方案的贡献和。
$n \leq 5\times 10^4$。
***
[评测链接](https://codeforces.com/contest/848/submission/97958691)
计数题,咕。
# [830E Perpetual Motion Machine](https://codeforces.com/contest/830/problem/E)
有 $n$ 台机器,每个机器有一个设定值 $d_i$,它可以定为任意非负整数。当某一台机器的设定值为 $d_i$ 时,它每秒会消耗 $d_i^2$ 的能量,如果某一对机器 $y,z$ 通过电线直接连接,每秒会产生 $d_y \times d_z$ 的能量。
现在,给出机器和电线的连接情况,试问是否存在一种设定 $n$ 个机器的设定值的方案,使得 $\exists i,d_i \neq 0$ 且能量的总生产值大于等于总消耗值。
$n, m \leq 10^5$。
***
[评测链接](https://codeforces.com/contest/830/submission/103998095)
奇怪的构造题。
如果有环,环上每个点权为 $1$ 即可。
如果有度数大于 $3$ 的,中间点权值为 $2$,周围点为 $1$ 即可。
如果有两个度数等于 $3$ 的,让它俩之间的点权值为 $2$,可以起到连接两者的效果。
如果所有点的度数 $\leq 2$,那肯定无解。
重点就在仅有一个度数为 $3$ 的情况。
考虑一条从中间点引出的链,长度为 $n$。
中间点的权值为 $a_n$。
则我们需要最大化
$$\sum_{i=1}^{n-1}(a_ia_{i+1}-a_i^2)$$
最后比较三条链的贡献和与 $a_n^2$ 的大小关系。
$$\begin{aligned}&\sum_{i=1}^{n-1}(a_ia_{i+1}-a_i^2)\\ =& -\frac 12(a_1^2-a_n^2+\sum_{i=1}^{n-1}(a_{i+1}-a_i)^2)\end{aligned}$$
根据均值不等式,$a_{i+1}-a_i$ 取等时原式取到最大值。
同时可以得到,有解的条件为 $\frac 1{n_1+1}+\frac 1{n_2+1}+\frac 1{n_3+1}\leq 1
所以我们令 a_n 为三条链长度的 \textrm{lcm} 即可。
但是这样是不行的,因为我们需要保证 a_i \leq 10^6 。
所以三条链如果都不小于 2 ,就令 n_1=n_2=n_3=2 ,或者两条链不小于 4 ,就令 n_1=2, n_2=n_3=4 ,这样就能接受了。
827F Dirty Arkady's Kitchen
给定一张无向图,每条边在时间 [l_i,r_i] 才能通过,通过花费 1 的时间。你不能在原地停留。
你在时刻 0 从 1 号点,求最快何时能到达 n 号点。
***
[评测链接](https://codeforces.com/contest/827/submission/101158328)
我们在一条边上反复横跳,发现到达一个点的时间奇偶性不变。
所以把每个点的奇偶分开考虑。这样我们拥有了 $2n$ 个点。
对于一个点,我们维护 $\textrm{maxi}_u$ 表示我能停留在 $u$ 号点的最大时刻。
如果一条边的起始时刻不小于 $\textrm{maxi}_u$,我们便能走这条边。
我们考虑通过类似 dijkstra 的方式,按照 $l$ 从小到大的顺序,求出每条边最早能够到达的时间。
问题在于,一条边能够被松弛必须要满足 $\textrm{maxi}_u \geq l$。那如果不满足,我们就先把边存在一个临时 vector 里,当 $\textrm{maxi}_u$ 被更新时,由于我们时按照 $l$ 排序的,一旦被更新,所有 vector 里的边都能走了。所以一条边至多会放入优先队列两次。
时间复杂度:$O(m\log m)$。
# [809E Surprise me!](https://codeforces.com/problemset/problem/809/E)
给定一棵 $n$ 个节点的树,每个点有一个权值 $a[i]$ ,保证 $a[i]$ 是一个 $1..n$ 的排列。
求 $\frac{1}{n(n-1)}\sum_{i=1}^n\sum_{j=1}^n\varphi(a_i*a_j)* dist(i,j)
其中, \varphi(x) 是欧拉函数, dist(i,j) 表示 i,j 两个节点在树上的距离。
***
[评测链接](https://codeforces.com/contest/809/submission/99370976)
好套路啊。
$$\varphi(xy)=\frac{\varphi(x)\varphi(y)\gcd(x, y)}{\varphi(\gcd(x, y))}$$
证明可以考虑 $\varphi(x)=x\sum_{p|x}(1-\frac 1p)$。
枚举 $\gcd$,建虚树,随便统计一下就好了。
# [804F Fake bullions](https://codeforces.com/problemset/problem/804/F)
给定一张 $n$ 个点的竞赛图,第 $i$ 个点上有 $S_i$ 个人,编号从 $0$ 到 $S_i-1$,其中的某一些人手上有真金条。
在时刻 $T$,如果从 $u$ 到 $v$ 有一条边,并且 $u$ 中第 $T\bmod S_u$ 个人手上有金条(无论真假),并且 $v$ 中第 $T \bmod S_v$ 个人没有金条,那么 $v$ 中第 $T \bmod S_v$ 个人会获得一个假金条。
当所有人手上的金条数目不再变化时,他们开始卖出金条,真金条一定会卖出去,而假金条可能卖出去也可能卖不出去。
现在从卖出金条最多的 $A$ 个点中随机选择 $B$ 个,问可能选出的城市集合有多少个。
$n \leq 5000$,$S \leq 10^6$。
***
[评测链接](https://codeforces.com/contest/804/submission/112343715)
这是一道二合一题。
考虑 $u \to v$,它们俩点上的人划分成 $\gcd(a_u, a_v)$ 个等价类,每一个类如果 $u$ 有至少一个,那么 $v$ 全有。
进一步地,一个强连通分量 $S$ 被划分成了 $\gcd_{u \in S} a_u$ 个等价类。每一类,要么每个点全有,要么全没有。
两个强连通分量之间的转移同两个点之间的转移。
这样我们得到了每个点能卖出去拥有的金条数目 $[l_i, r_i]$。
我们枚举哪个点是所有点中卖出金条第 $B$ 多的。假设是 $u$。
那么 $r_i \geq l_u$ 的必选,$r_u < l_i$ 的必不选,剩下的可选可不选,组合数算算即可。
# [798E Mike and code of a permutation](https://codeforces.com/problemset/problem/798/E)
对于一个排列 $P=[p_1,p_2,\dots,p_n]$,定义它的编码 $A$ 为:对于每个 $i$,找到第一个未被标记过的位置 $j$ 满足 $p_j>p_i$,令 $a_i=j$,并打上标记;若没有合法的,则 $a_i=-1$。
现给出一个编码 $A$(除 $-1$ 外各不相同),请输出一个合法的 $P$。
***
[评测链接](https://codeforces.com/contest/798/submission/105259575)
不太会,咕了。
# [794G Replace All](https://codeforces.com/problemset/problem/794/G)
给两个包含 `A`,`B`,`?` 的串,`?` 可以是 `A` 或 `B`,求所有 `?` 的情况下,求下面这个东西的和:统计有多少对长度 $\le n$ 的 `01` 串 $(S,T)$ 使得把所有 `A` 换成 $S$,`B` 换成 $T$ 使得两个串相等。
$|S|, |T|, n \leq 3 \times 10^5$。
***
[评测链接](https://codeforces.com/contest/794/submission/96344454)
假设 $|S|\geq |T|
考虑两个串从头开始匹配,直到两个字符不同。
则可以得到:S=TTTTT\ldots S' ,其中 S' 是 S 的一个前缀。
这样我们发现,T 是 S 的一个周期。
同时,我们发现 S 的最小周期必须是 T 的因数,不然 S' 后半部分没办法继续匹配。
所以这个周期为 \gcd(|S|, |T|) 的因数,我们确定了这 \gcd(|S|, |T|) 位,两个串就能确定了。
若两个串中有 a_1, b_1 个 S ,a_2, b_2 个 T ,则还需要满足:
(a_1-b_2)|S|=(a_2-b_1)|T|
如果 a_1=b_2 且 a_2=b_1 ,则答案为
\begin{aligned}& \sum_{i=1}^n\sum_{j=1}^n2^{\gcd(i, j)}\\ =& \sum_{i=1}^n\lfloor\frac ni\rfloor^2\sum_{d|n}2^d\mu(\frac id)\end{aligned}
否则,设 a = a_1-b_2, b = a_2 - b_1 ,则有 a|S|=b|T| ,得到
\frac a{\gcd(a, b)}=\frac {|S|}{\gcd(|S|, |T|)}
所以 \gcd(a, b) 能取的范围为:
\lfloor\frac {n}{\max(\frac a{\gcd(a, b)}, \frac b{\gcd(a, b)})}\rfloor
答案为 2 的幂的前缀和。
我们设 a, b 的贡献为 f_{a, b} 。
设第一个串有 p 个 ?,第二个串有 q 个 ?,最初的 a, b 为 a', b' ,答案为:
\sum_{i=0}^p\sum_{j=0}^qf_{a'+i-j, b'+p-q-(i-j)}\binom pi\binom qj
经典套路:枚举 i-j 。
\begin{aligned}&\sum_{d=0}^{\max(p, q)}f_{a'+d, b'+p-q-d}\sum_{j=0}^q\binom{p}{p-j-d}\binom{q}{j}\\ =&\sum_{d=0}^{\max(p, q)}f_{a'+d, b'+p-q-d}\binom{p+q}{p-d}\end{aligned}
这道题就做完了。
793G Oleg and chess
有一个 n\times n 的矩阵,每行每列至多能放一个棋子,另外有 q 个矩形的区域不能放棋子(这些矩形区域互不相交),问最多能放多少个棋子。
***
[评测链接](https://codeforces.com/contest/793/submission/104100874)
$(i, j)$ 能选,则 $i \to n + j$,之后 $s \to [1, n], [n+1, 2n] \to t$,跑最大流。
这样复杂度不能接受。
考虑优化建图。扫描线从左往右扫过去,set 维护横坐标连续段,当扫到一个矩形的左边时,暴力遍历 set 区间。由于矩形右边会把这个区间推平,所以总共只会访问 $O(n)$ 次 set。
# [793F Julia the snail](https://codeforces.com/problemset/problem/793/F)
有一个长为 $n$ 的杆,上面有 $m$ 条绳子,每条绳子可以让蜗牛从 $l_i$ 爬到 $r_i$(中途不能离开),保证 $r_i$ 各不相同。蜗牛也可以自然下落。
现在有 $q$ 次询问,询问 $x$ 出发,途中高度不能低于 $x$ 或高于 $y$,问最高能爬到的位置。
$n,m,q\leq 10^5$。
***
[评测链接](https://codeforces.com/contest/793/submission/98369694)
对右端点排序,考虑维护每个左端点的贡献。
设 $f_i$ 表示 $i$ 号点最高能到哪。
一条绳子就是让 $i \leq l, f_i \geq l$ 的 $f_i$ 和 $r$ 取 $\max$。
SegmentTree Beats 即可。
# [788D Finding lines](https://codeforces.com/problemset/problem/788/D)
二维平面上有共 $n+m$ 条未知的平行于坐标轴的直线。
你每次可以询问一个平面上点,交互库将返回该点与离它最近的直线之间的距离。
你要在 $3 \times 10^5$ 次询问内确定这 $n$ 条直线。
询问和答案 $\in [-10^8, 10^8]
***
[评测链接](https://codeforces.com/contest/788/submission/101618204)
如果询问 $(x, x)$ 答案是 $0$,那我们再询问 $(x, rand())$,如果是 $0$ 就是平行于 $y$ 轴,否则就是 $x$ 轴。
考虑如果现在 $(x, x)$ 答案是 $k$,距离最近的点是一个我们已经知道的点 $(x-k,x-k)$,那么下次问 $(x+k, x+k)$,如果答案是 $2k$,说明我们还没有过两个点的中点,继续这个流程,否则直接一步走到。
但是这样的复杂度是 $n\sqrt n$ 的,所以我们最初开始询问的时候不要从 $1$ 开始,而是一个较大的数,比如 $1000$。
# [786E ALT](https://codeforces.com/problemset/problem/786/E)
给一颗 $n$ 个节点的树,每个边上有一个守卫。有 $m$ 个居民,每个居民有一个散步路径(两个节点的树上最短路)。一个居民高兴当且仅当他获得了一个宠物或者他散步的路径上所有的守卫都有宠物。宠物可以分配给居民或者守卫者。求最少需要几只宠物才能让所有居民高兴。输出方案。
$n,m \leq 2\times 10^4$。
***
[评测链接](https://codeforces.com/contest/786/submission/98097394)
显然是最小割。
显然树剖优化。
# [778E Selling Numbers](https://codeforces.com/problemset/problem/778/E)
给定 $n$ 个数字串和一个包含数字和 `?` 的串 |A|。
给定每个数位的贡献,你需要在每个 `?` 填入一个数字。使得这个串和 $n$ 个数字串分别相加构成的 $n$ 个数的数位贡献和最大。
$n, |A| \leq 1000$。
***
[评测链接](https://codeforces.com/contest/778/submission/98513692)
见 `1188D Make Equal`。
# [773F Test Data Generation](https://codeforces.com/problemset/problem/773/F)
给定 $n, a$,求从 $[1, a]$ 中选出至多 $n$ 个数,满足选了奇数个数,且 $2| \max\{a\}$且 $2\gcd\{a\}\not|\max\{a\}$的方案数。
$n \leq 3 \times 10^4$,$a \leq 10^9$。
***
[评测链接](https://codeforces.com/contest/773/submission/96952381)
计数题,咕。
# [765G Math, math everywhere](http://codeforces.com/problemset/problem/765/G)
给定 $N$ 的因式分解形式 $\prod_{i=1}^np_i^{\alpha_i}$ 和一个长为 $m$ 的字符串 $s$。
求 $k$ 的个数,使得 $0\leq k<N$ 且
$$\gcd(k+i,N)=1 \text{ if and only if }s_i=1$$
模 $10^9+7$。
$m \leq 40$,$n\leq 5\times 10^5$,$p_i, \alpha_i \leq 10^9$。
***
[评测链接](https://codeforces.com/contest/765/submission/96778265)
首先我们可以发现,若我们对于每个 $p_i$,确定了 $k \bmod p_i$ 的值,那么 $s$ 的值可以唯一确定,为
$$\begin{cases}1 & \exists i,s.t. p_i|(k+i) \\ 0 & \textrm{otherwise} \end{cases}$$
由此可以得出,$\alpha$ 是没用实际作用的,我们最后将答案乘 $\prod p_i^{\alpha_i-1}$ 即可。
我们此时产生了一个幼稚的想法:设 $f_{i, t}$ 表示前 $i$ 个质数,字符串状态为 $t$ 的方案数。每次枚举 $k\bmod p_i$ 的值进行转移。
这样的复杂度显然是不能接受的。但是实际上,那些 $p_i \geq m$ 的数,最多会在字符串中出现一次。如果我们先算好了 $p_i < m$,得到了一些状态。之后对于每个状态我们只用考虑每个质数在哪个位置上出现即可,不用考虑具体放置的位置。
比如当前的状态为 `111111111`,目标状态为 `100101100`。我们只用考虑有 $5$ 个 `1` 变成了 `0`,不用考虑它们的位置和顺序关系。
我们设 $f_{i, j}$ 表示目前还有 $i$ 个 `0` 需要被填,$j$ 个 `0` 已经被填,现在可以再填。则有转移:
$f'_{i, j}=\begin{cases}j\times f_{i, j} \\ i\times f_{i+1, j-1} & j\neq 0\end{cases}
当然,这个转移可以轻松地优化到线性。
那对于 p_i < m 的部分,最多只有 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37 这 12 个质数。我们猜测状态数不会太多。简单打表可以发现,2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37 全部包含,状态数是很少的。
于是我们就有了一个似乎很优秀的做法。这也是最初的 std 所做的全部。
但是,这样考虑真的正确吗?
我们仔细分析我们的做法,我们把所有状态相同存储在一起。也就是说,如果状态过于稠密,集中在全 1 或者几乎全 1 周围,那么这并不是最极端的情况。我们把 2, 3 两个贡献次数过多的数字去掉,发现状态爆炸性地增长,完全不能接受。
怎么办呢?我们考虑继续分离 p_i < m 的质数。
我们从小往大不断加数(除去 2, 3 ),到 23 ,状态数达到 10^7 级别。于是我们把 \leq 23 的质数分为一堆,用第一种方式处理,29, 31, 37 重新考虑一种方式。
首先我们能考虑到,29 \geq \frac m2 。也就是说这三个质数只会在字符串里出现至多两次。我们考虑能不能把两次通过某种方式处理呢?
其实这一步是很自然的,我们将前两种方式融合起来(官方题解:“杂种 dp”)。因为 29 已经离 40 不远了。我们直接存下字符串前 11 位,后 11 位的状态,而中间的 18 位,由于最多只出现一次,我们再用第二种方式处理。
这样,我们就把很多不同的状态化解成相同的状态,经过实验,继承来自 \leq 23 的状态,转移三个数,最终的状态数没有超过 10^7 。
这样我们就大致看清了这道题的轮廓。接下来是很多的细节。
首先,std::map 显然不能进行 10^7 量级的运算,unordered_map 的空间常数也十分巨大(大概数十倍)。所以我们需要手动实现 \textrm{hashtable} 。
当然了,第一部分可以用 map,只要在做 23 的时候,不要去重,直接插到 \textrm{hashtable} 就好。我实现的时候把 19 也跳了,似乎快了微不足道一点点。
其次,仅仅按照上面的写法比较难通过(我最后到了 9 秒)。我们可以算完 29 算 31 的时候把两边边缘各两位放到自由的部分里,37 当然也可以不过我的 \textrm{hash} 用的是 unsigned int 所以存 37 的时候会出问题,就没有再改 37 了(因为随便改改就很快了)。
代码写得很麻,因为上面的细节都是写完了又重构写完了又重构总结出来的...
756E Byteland coins
你现在有 n 种金币,第 i 种金币的面额是 \prod_{j=1}^{i-1} a_j ,有 b_i 枚。保证对于一个相同的 x ,面值为 x 的金币不会超过 20 种。
求凑出总面值为 m 的方案数,模 10^9+7 。
***
[评测链接](https://codeforces.com/contest/756/submission/96408614)
我们设 $f_{i, j}$ 表示前 $i$ 种金币,总面额为 $j$ 的方案数。$d_i$ 表示 $\prod_{j=1}^i a_j$,$k=20$ 表示 $a_i=1$ 的连续段最大长度。
显然,$f_{i, j}$ 给答案贡献仅当 $j\equiv m\pmod {d_i}$。因为 $i$ 之后的面额都是 $d_i$ 的倍数。
那么,我们设 $g_{i, j}$ 表示 $f_{i, d_i\times j+m\bmod d_i}$。设 $sz_i = \max\{j|g_{i, j}\neq 0\}$,则有
$$sz_i\leq \sum_{j=1}^i b_j\frac{d_j}{d_i}$$
这是因为只有 $\frac{d_i}{d_j}$ 的倍数才是有可能对答案有贡献的 $j$,共 $b_j\frac{d_j}{d_i}$ 个。
$d_i$ 至多往前 $k$ 步变化一次,一次变化是除以一个不为 $1$ 的 $a_j$,也就是至少缩小一半。因此:
$$\sum_{i=1}^n sz_i\leq \sum_{i=1}^n\sum_{j=1}^ib_j\frac{d_j}{d_i}=\sum_{j=1}^nb_j\sum_{i=j}^n\frac{d_j}{d_i}\leq \sum_{j=1}^n b_j (\frac {k}{2^0}+\frac{k}{2^1}+\frac{k}{2^2}+\ldots)=2k\sum_{j=1}^n b_j$$
感性地理解为,小的面值再往后 $k\log b_i$ 步就无用了,并且作用次次减半。
所以,$\sum sz_i$ 的范围是可以接受的。
我们用前缀和优化多重背包,复杂度正好是 $\sum sz_i$。
如何求出 $m \bmod d_i$?实现一个线性复杂度的高精度就好。当 $a_i=1$ 的时候直接继承,这样经过至多 $\log_2m$ 次,$\prod a_i> m$,此时退出即可。
时间复杂度:$O(\log^2m+k\sum b_i)$。
因为高精度本来就比较恼人所以代码用了很多硬编码。
# [755G PolandBall and Many Other Balls](https://codeforces.com/problemset/problem/755/G)
有一排 $n$ 个球,定义一个组可以只包含一个球或者包含两个相邻的球。现在一个球只能分到一个组中,求从这些球中取出 $k$ 组的方案数。
$n\le 10^9$,$k<2^{15}$。
***
[评测链接](https://codeforces.com/contest/755/submission/98107814)
计数题,咕。
# [750H New Year and Snowy Grid](https://codeforces.com/problemset/problem/750/H)
给一个 $h\times w$ 的棋盘,有障碍。$q$ 次询问,每次把 $k$ 个点变成障碍后询问能否找到两条从 $(1,1)$ 到 $(n,n)$ 的不相交的路径,询问独立。需要通过交互实现强制在线。
$h, w \leq 10^3$,$q \leq 10^4$,$k \leq 10$。
***
[评测链接](https://codeforces.com/contest/750/submission/95939231)
我们考虑,若询问的是 $(1, 1)$ 与 $(h, w)$ 是否连通,该如何解决。
不难发现,我们若在网格外加一层 `#`,则 $(1, 1)$ 与 $(h, w)$ 通过 `.` 四连通当且仅当 $(h + 1, 0)$ 与 $(0, w + 1)$ 通过 `#` 无法八连通。
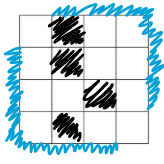
如图,蓝色为网格外加的一层 `#`,此时 `#` 八连通,所以 `.` 无法四连通。
同理,我们可以得出,`.` 双四连通(存在两条不交的四连通路径)当且仅当 `#` 无法“几乎”八连通。“几乎”八连通指的是存在一种方案使得仅添加一个 `#` 即可八连通。
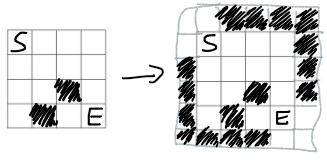
如图,$S$ 到 $E$ 仅存在一条路径,所以黑色是“几乎”八连通的。
那么我们现在的问题变为,添加 $k$ 个 `#` 后,如何判定 `#` 是否“几乎”八连通。
我们考虑首先对于每个连通块,求出已经“几乎”八连通的连通块邻居,即使它们有可能还没有和左下右上连通。在网格上走至多两步走到的连通块都是。
我们把可能 `No` 的情况分为两种:
1. 两个新的 `#` 切比雪夫距离 $\leq 2$,并且它们一个和左下连通,一个和右上连通。
2. 一些新的 `#` 使得一些原来孤立的连通块和左下连通了,而这个连通块又有“几乎”八连通的邻居现在和右上连通。
第一种情况 $k^2$ 枚举即可。
第二种情况,我们发现这样的连通块至多只有 $O(dk)$ 种,其中 $d=8$ 表示一个格子的相邻格子数,枚举每个连通块的“几乎”八连通邻居,看看是否和右上连通。最多 $O(d^2)$ 种,总复杂度 $O(d^3k)$。
实现上我用了可撤销并查集。
注意空间限制只有 256MB,不要放飞自我。
时间复杂度:$O(hwd^2+qd^3k)$。
# [750G New Year and Binary Tree Paths](https://codeforces.com/problemset/problem/750/G)
一颗无穷个节点的完全二叉树。
求有多少条树上的简单路径编号和为 $s$。
$s \leq 10^{15}$。
***
[评测链接](https://codeforces.com/contest/750/submission/95547772)
先考虑一条自上向下的链的情况。
我们可以证明,我们选择了链长度,合法的路径至多有一条。
设起点为 $x$,链长为 $h$。
我们始终往左走得到的值为:$x\sum_{i=0}^{h-1}2^i=x(2^{h}-1)
如果第 i 步往右走,新产生的值为 2^i-1 。
所以,能够走到的数的取值范围为:
[x(2^h-1), x(2^h-1)+(2^h-h)]
可以发现,每个 x 的范围是不交的。
于是我们枚举 h 即可。贪心地走即可。
如果是一条路径,我们确定了两边的长度 h_1, h_2 ,同样也可以证明路径只有至多一条。
但是我们不能贪心地走了。
我们考虑我们现在有 2^1-1,2^2-1,2^3-1,\ldots 2^{h_1}-1,2^1-1,2^2-1,\ldots 2^{h_2}-1 ,我们现在要凑出一个数 ret 。
可以给每个数加 1 。假如选了 n 个,我们要凑出 n+ret 。
设 f_{i, j, 0/1} 表示前 i 位,选了 j 个数,是否进位时的方案数。
时间复杂度:O(\log ^5 s) 。
739E Gosha is hunting
你要抓神奇宝贝!
现在一共有 n 只神奇宝贝。
你有 a 个『宝贝球』和 b 个『超级球』。
『宝贝球』抓到第 i 只神奇宝贝的概率是 p_i ,『超级球』抓到的概率则是 u_i 。
不能往同一只神奇宝贝上使用超过一个同种的『球』,但是可以往同一只上既使用『宝贝球』又使用『超级球』(都抓到算一个)。
请合理分配每个球抓谁,使得你抓到神奇宝贝的总个数期望最大,并输出这个值。
***
[评测链接](https://codeforces.com/contest/739/submission/98991013)
很显然的网络流模型。
能网络流说明他是凸的,wqs 二分。
# [720F Array Covering](https://codeforces.com/problemset/problem/720/F)
给定一个长度为 $n$ 的序列 $a$。
你需要选出 $k$ 个不同的子序列 $[l_i, r_i]$,使得它们的并为 $[1, n]$,求子序列和的最大值。
$n \leq 10^5$。
***
[评测链接](https://codeforces.com/contest/720/submission/99960458)
首先,不要看到标签里的 `*3100` 就以为这是一道水题。
这题破了我单题代码最长纪录(打表除外):$10.49K$。
结论 $1$:如果已经有一种方案,那么我们把其中的每个子序列 $[l_i, r_i]$ 向左右扩展至权值最大的位置,显然还是一种合法的方案。
结论 $2$:权值前 $\max(0, k-n)$ 大的子序列一定会被选。
证明:$k\leq n$ 显然。$k > n$ 的情况下,$k-\max(0, k-n)\geq n$,所以我们剩下了不少于 $n$ 个子序列。如果在这些不优的子序列中,有一个序列没有起到将并集扩大的作用,那么这个子序列是“自由”的,我们把它替换成最优的子序列,显然方案仍然是合法的,全集大小为 $n$,所以我们留下多于 $n$ 个不优的子序列显然是不好的。
我们从 $\max(0, k-n)$ 到 $k$ 枚举使用了多少个最大的子序列,设其为 $x$,它们的并集为 $S$。
结论 $3$:存在一种最优方案,使得对于某个 $x$,剩下的 $k-x$ 个不优的子序列的交集 $\subset S$。
证明:反证法:假设交集 $\not\subset S$。假如两个子序列不为包含关系,设他们为 $[l_1, r_1], [l_2, r_2]$($l_1\leq l_2\leq r_1 \leq r_2$),若它们的交为 $[l_u, r_u]$,则我们可以将其变为 $[l_1, r_2]$ 和 $[l_u, r_u]$ 两个子序列,转化为包含关系。若为包含关系,则 $[l_u, r_u]$ 是“自由”的。由于交集 $\not\subset S$,说明 $[l_u, r_u]$ 不为最优的子序列之一。那我们把 $[l_u, r_u]$ 转化为最优的子序列(即 `x++` ),显然更优。
于是我们先选出 $\max(0, k-n)$ 个最大的子序列。我们二分这个权值,再用主席树维护两维限制即可。
之后我们枚举 $x$,维护 $S$,用 $k-x$ 个交集 $\in S$ 的区间覆盖没有被覆盖的位置。
我们用 `set` 维护 $S$ 和 $S$ 的补集。再把 $S$ 连续的一段作为一个元素放到堆中,贡献为(这一段的和 - 这一段的前缀最大值 - 这一段的后缀最大值),这么算的原因是结论 $1$。于是我们需要两棵主席树。
再用堆维护一下下一个最大的子段和。
所以我们总共有 $4$ 个堆,$2$ 棵主席树,$2$ 个 set。
时间复杂度:$O(n\log^2 n)$。
# [720D Slalom](https://codeforces.com/problemset/problem/720/D)
一个 $n \times m$ 的网格,其中有 $k$ 个矩形障碍,保证这些障碍不重叠。求从 $(1,1)$ 走到 $(n,m)$,每步只能往右或往上走,不经过任何障碍的方案数。
两种方案被视为不同,当且仅当存在一个障碍,它在第一种方案里被从右侧绕过,而在第二种方案里被从左侧绕过(第一种左,第二种右同理)。
$n, m \leq 10^6$,$k \leq 10^5$。
***
[评测链接](https://codeforces.com/contest/720/submission/98658757)
设 $f_{i, j}$ 表示走到 $(i, j)$ 的方案数。
既然两种方案不同当且仅当跨过的矩形集合不同,那我们把方案数存在每个矩形的上边界上。也即若 $(i-1, j)$ 为空,$f_{i, j}=0$。
当扫到第 $i$ 行的一个矩形时,设其上边界为 $w$,则
$$f_{i, w}=\sum_{j=l}^w f_{i-1, w}$$
$l$ 为第 $i-1$ 行最后一个上边界 $\leq w$ 的矩形位置。
那么维护 $f$ 我们用线段树,找 $l$ 我们用 set。
# [718E Matvey's Birthday](http://codeforces.com/problemset/problem/718/E)
给定一个仅包含 `a`~`h` 的字符串。
有一个 $n$ 个结点的无向图,编号为 $0$ 到 $n−1$。结点 $i$ 与结点 $j$ 间有边相连当且仅当 $|i-j|=1$ 或 $S_i=S_j$。
求这个无向图的直径和有多少对点间的最短距离与直径相同。
$n \leq 10^5$。
***
[评测链接](https://codeforces.com/contest/718/submission/100886688)
设 $\textrm{dis1}_{i, j}$ 表示从点 $i$ 走到任意字符为 $j$ 的位置的最短距离。
如何求呢?我们再设 $\textrm{dis2}_{i, j}$ 表示从字符 $i$ 走到字符 $j$ 的最短距离。用它来更新。
那么两点之间的距离 $\textrm{dis}(x, y)=\min(|x-y|,1+\min_k\{\textrm{dis1}_{x, k}+\textrm{dis1}_{y, k}\})
为什么一定加 1 呢,因为总存在一个 k 满足我们使用了传送。不使用传送就变成前者了。
这样的复杂度是 O(n^2) 的。
如何优化?考虑 0 \leq \textrm{dis1}_{y, k}-\textrm{dis2}_{a_y, k} \leq 1 。
我们把它压成一个状态 S 。若 S 相同,后面的值就相同。
而我们又发现,答案 \leq 15 。所以我们暴力计算 j-i \leq 15 的 j ,再把剩下的 j 存到对应的状态里,每次枚举每种状态统计答案,这样我们就做完了。
715E Complete the Permutations
给定两个排列 p,q ,但是其中有些位置未知,用 0 表示。
现在让你补全两个排列,定义两个排列 p,q 之间的距离为每次选择 p 中两个元素交换,使其变成 q 的最小次数。
现在你需求出对于 i \in [0,n-1] 求出补全后相似度为 i 的方案数。
***
[评测链接](https://codeforces.com/contest/715/submission/100812624)
计数题,咕。
# [713E Sonya Partymaker](https://codeforces.com/problemset/problem/713/E)
一个长度为 $m$ 的环,最初有 $n$ 个点上有人。
每秒可以让所有人都走一步(可以选择每个人的方向,但中途不能变换方向)。
问使所有点都被走到的最短时间。
$n \leq 10^5$,$m \leq 10^9$。
***
[评测链接](https://codeforces.com/contest/713/submission/94955099)
考虑二分答案 $k$。
首先,环的问题怎么解决?我们找到相邻两人距离最大的位置,在最优情况下,这里一定是两边的人相向行走。我们以此断开环。
问题转化为序列上的问题。
设 $f_i$ 表示前 $i$ 个人最远能覆盖到哪里。
$f_i = \begin{cases}a_i+k & f_{i-1}\geq a_i\\ a_i & f_{i-1} \geq a_i-k \\ \textrm{gg} & \textrm{else}\end{cases}
但是还有一种情况!考虑 i 之前的一小段没有被覆盖,如果使用 i 来覆盖大材小用。此时我们可以我们使用 i+1 向前覆盖,i 向后覆盖。那有没有更优的策略呢?(比如使用 i+2 )显然是没必要的。因为我们只需要满足 i 能够向后覆盖。
708E Student's Camp
有一个 (n+2) \times m 的网格。
除了第一行和最后一行,其他每一行每一天最左边和最右边的格子都有 p 的概率消失。
求 k 天后,网格始终保持连通的概率。
***
[评测链接](https://codeforces.com/contest/708/submission/91684731)
设 $f_{i, l, r}$ 表示前 $i$ 行连通,第 $i$ 行是 $[l, r]$ 的概率。
$$f_{i, l, r} = P_{l-1}P_{m-r}\sum_{[l', r']\cap [l, r] \neq \varnothing}f_{i-1, l', r'}$$
$f$ 的状态数有 $nm^2$ 个,考虑优化。
其中 $P_i$ 表示消失 $i$ 个的方案数,$P_i=\binom kip^i(1-p)^{k-i}$。
设 $\textrm{sum}_{i, r}$ 表示 $\sum_{j=1}^rf_{i, j, r}$,$\textrm{ss}_{i, r}$ 表示 $\sum_{j=1}^r\textrm{sum}_{i, j}$。
由于左右是对称的,所以后缀和和后缀和的和不用记。
$$f_{i, l, r}=P_{l-1}P_{m-r}(\textrm{ss}_{i-1, m}-\textrm{ss}_{i-1, l-1}-\textrm{ss}_{i-1, n-r})$$
$\begin{aligned}\textrm{sum}_{i, r}=&\sum_{j=1}^rf_{i, j, r}\\ =&\sum_{j=1}^rP_{j-1}P_{m-r}(\textrm{ss}_{i-1, m}-\textrm{ss}_{i-1, j-1}-\textrm{ss}_{i-1, n-r})\\ =&P_{m-r}(-\sum_{j=1}^rP_{j-1}\textrm{ss}_{i-1, j-1}+\sum_{j=1}^r\textrm{ss}_{i-1, m}-\textrm{ss}_{i-1, n-r})\end{aligned}
再记录 \textrm{sp}_{i, r}=\sum_{j=1}^rP_{j-1}\textrm{ss}_{i-1, j-1} 即可。
时间复杂度:O(nm) 。
704D Captain America
平面上有 n 个点,第 i 个点的坐标为 (x_i, y_i) 。
每个点都要被涂色,涂成红色需要 r 元,涂成蓝色需要 b 元。
另外有 m 个限制,每个限制有两种可能:
1 l d 表示在直线 x = l 上,涂成两种颜色的点的数量之差不超过 d 。
2 l d 表示在直线 y = l 上,涂成两种颜色的点的数量之差不超过 d 。
要求构造出一种涂色方案使得满足所有限制且总花费最少,或判断无法构造。
***
[评测链接](https://codeforces.com/contest/704/submission/98092744)
设 $(a, b)$ 表示最低流量为 $a$,最高流量为 $b$ 的边。
对于每个点 $(x_i, y_i)$,从 $x_i$ 向 $y_i'$ 连 $(0, 1)$ 的边。
设 $c$ 表示这条线上的点的个数。
$s$ 往 $x_i$ 连 $(\frac {c-d}2, \frac {c+d}2)$ 的边。$d$ 选最小的。
$y_i'$ 往 $t$ 连 $(\frac {c-d}2, \frac {c+d}2)$ 的边。
上下界费用流即可。
# [700E Cool Slogans](http://codeforces.com/problemset/problem/700/E)
给定一个字符串 $S$,要求构造字符串序列 $s_1,s_2,\ldots,s_k$,满足任意 $s_i$ 都是 $S$ 的子串,且任意 $i\in[2,n]$,都有 $s_{i-1}$ 在 $s_i$ 中出现了至少 $2$ 次(可以有重叠部分,只要起始、结尾位置不同即可)。
求可能的最大的 $k$ 的值(即序列的最大可能长度)。
$n \leq 2 \times 10^5$。
***
[评测链接](https://codeforces.com/contest/700/submission/91467868)
后缀自动机建出 parent 树,倍增。
# [698F Coprime Permutation](https://codeforces.com/problemset/problem/698/F)
求有多少种排列 $p$ 满足对于任意 $i, j$,都有
$$[\gcd(i, j)=1]=[\gcd(p_i, p_j)=1]$$
对 $10^9+7$ 取模。
$n \leq 10^6$。
***
[评测链接](https://codeforces.com/contest/698/submission/98995301)
不太会,咕了。
# [679E Bear and Bad Powers of 42](https://codeforces.com/problemset/problem/679/E)
定义一个正整数是坏的,当且仅当它是 $42$ 的次幂,否则它是好的。
给定一个长度为 $n$ 的序列 $a_i$,保证初始时所有数都是好的。
有 $q$ 次操作,每次操作有三种可能:
- `1 i` 查询 $a_i$。
- `2 l r x` 将 $a_{l\dots r}$ 赋值为一个好的数 $x$。
- `3 l r x` 将 $a_{l \dots r}$ 都加上 $x$,重复这一过程直到所有数都变好。
$n,q \le 10^5$,$a_i,x \le 10^9$。
***
[评测链接](https://codeforces.com/contest/679/submission/88844731)
线段树每个结点记录一个 $d$ 表示区间内离 $42$ 的幂最近的是多少。
修改时如果某个区间 $d$ 小于 $0$ 了,继续进儿子。
为什么复杂度是对的?操作 $3$ 不用说,操作 $2$ 每次让 $\log$ 个区间可能进行操作,而假如一个区间的值全部相同,我们可以 $O(1)$ 修改。
时间复杂度:$O(n \log n \log_{42} a)$。
# [666E Forensic Examination](https://codeforces.com/problemset/problem/666/E)
给你一个串 $S$ 以及一个字符串数组 $T_{1\ldots m}$,$q$ 次询问,每次问 $S$ 的子串 $S[p_l\ldots p_r]$ 在 $T_{l\ldots r}$ 中的哪个串里的出现次数最多,并输出出现次数。
如有多解输出最靠前的那一个。
$|S|, q \leq 5 \times 10^5$,$m \leq 5 \times 10^4$。
***
[评测链接](https://codeforces.com/contest/666/submission/91623191)
建出 $S$ 的后缀自动机。
首先,$S[p_l\ldots p_r]$ 怎么定位?我们预处理 $S[1\ldots i]$ 的位置,之后跳后缀链接能得到 $S[1\ldots i]$ 的一个后缀。为了保证复杂度,我们预处理后缀链接的倍增数组。
之后 $T$ 的一个区间怎么做?把每个串在后缀自动机上匹配,线段树维护一下终止位置。
之后线段树合并即可。
# [666D Chain Reaction](https://codeforces.com/problemset/problem/666/D)
给定平面直角坐标系中的**四个整点**,问是否存在四个整数坐标,满足:
第 $1$ 个点能够仅通过竖直**或者**水平移动到达第 $1$ 个坐标(也就是说横坐标或者纵坐标相同),第 $2, 3, 4$ 个点类似。
且这四个新的整数坐标形成了面积非负的正方形的四个顶点(也就是说不能重合)。
且这个正方形的边必须平行于坐标轴(不是斜着的)。
如果存在这样的四个坐标,则尽量最小化对应点移动的距离的最大值。
(形式化地说,假设第 $i$ 个点移动的距离为 $d_i$,你需要最小化 $\max\limits_{i=1}^{4} d_i$)
如果不存在这样的坐标,输出 `-1`。
否则输出最小化的 $\max\limits_{i=1}^{4} d_i$,以及那四个坐标。
有 $t$ 组询问。
$t \leq 50$。
***
[评测链接](https://codeforces.com/contest/666/submission/106714320)
什么烂题。。。
$4!$ 枚举每个点走的方向,之后分类讨论。
* 两条横线两条竖线,形成四个交点,判断它是否是正方形。
* 两条横线一条竖线,正方形的两个交点和边长都确定了,就两种可能的位置。
* 两条横线,这样边长确定了,答案的式子形如 $\min\sum |x_i-x|$,取他们的中位数即可。
* 其他情况显然无解。
# [653G Move by Prime](https://codeforces.com/problemset/problem/653/G)
给你一个长度为 $n$ 的数列 $a_i$,你可以进行任意次操作:将其中一个数乘上或者除以一个质数。使得最终所有数相同,并使得操作数尽可能小。现在我们想要知道 $a_i$ 的所有子序列的操作数之和是多少。
$n \leq 3 \times 10^5$。
***
[评测链接](https://codeforces.com/contest/653/submission/98115112)
每个质数是独立的。
对于每个质数,式子形如 $\min \sum |x_i-x|$,取他们的中位数即可,在左边的贡献为 $-x_i$,在右面的为 $x_i$。
问题来了,对于所有子序列算这个,怎么办?
考虑排名为 $i$ 的数贡献的次数。
在左边选 $a$ 个,在右边 $b$ 个的贡献为
$$\begin{cases}x_i & a < b \\ -x_i &a > b\\ 0 & a=b\end{cases}$$
也就是 $\textrm{sgn}(a-b)x_i$。
枚举 $a+i-b$,相当于我们把左边不选的和右边选的这些数挑出来的方案数。
所以贡献为 $$\sum_{j=i}^{n-1}\binom {n-1}{j}-\sum_{j=0}^{i-2}\binom {n-1}{j}$$。预处理组合数前缀和即可。
# [645G Armistice Area Apportionment](https://codeforces.com/problemset/problem/645/G)
给定两点 $P(a,0), Q(-a,0)$,现在在平面上有 $n$ 个点,以 $n$ 个点为圆心作 $n$ 个过 $P$ 的圆。求所有圆交点中与点 $Q$ 最近的交点,输出该交点到点 $Q$ 的距离。
$n \leq 10^5$。
***
[评测链接](https://codeforces.com/contest/645/submission/95650280)
计算几何滚出 OI!
# [639F Bear and Chemistry](https://codeforces.com/problemset/problem/639/F)
给定一张 $n$ 个点 $m$ 条边的初始无向图。
$q$ 次询问,每次询问给定一个点集 $V$ 和边集 $E$。
你需要判断,将 $E$ 中的边加入初始无向图之后,$V$ 中任意两个点 $x,y$ 是否都能**在每条边至多经过一次**的情况下从 $x$ 到 $y$ 再回到 $x$。
$n,m,q,\sum |V|, \sum |E| \le 3 \times 10^5$,强制在线。
***
[评测链接](https://codeforces.com/contest/639/submission/86889679)
首先询问等价于 $V$ 中的所有点是否都在同一个边双内。
说到边双,我们想到对一棵生成树的路径打标记。
由于原始图不会被删,我们可以先求出原图的生成树。
之后每条边便是对一条路径打标记,或者连通两棵树。
既然要加边,LCT 就好了。
# [627F Island Puzzle](https://codeforces.com/problemset/problem/627/F)
给定一棵 $n$ 个点的树,每个点上都有一个 $[0,n-1]$ 的数,任意两点上的数都不同。
每次你可以交换 $0$ 所在的点和与其相连的任一点上的数,同时你可以最多加入一条边。
给定目标状态,你需要在加入的边数尽量小的前提下,求出最少的步数,或者判断无法达成目标。
$n \leq 2 \times 10^5$。
***
[评测链接](https://codeforces.com/contest/627/submission/105425625)
加一条边后变为基环树。
先把 $0$ 走到终点。
我们考虑哪些位置能够改变。
不在环上的显然不能改变。在环上的会平移若干位,但是相对顺序不会变。
随便判一下就好了。
# [627E Orchestra](https://codeforces.com/problemset/problem/627/E)
在一个 $r \times c$ 的矩阵中有 $n$ 个点,问有多少个连续子矩阵至少包含 $k$ 个点。
$r,c,n \le 3 \times 10^3$,$k \le 10$。
***
[评测链接](https://codeforces.com/contest/627/submission/98161335)
枚举上边界,再从小往大枚举下边界,用链表维护现在所有的点的位置。
$f_i$ 表示左边界为 $i$,至少要到哪里才能包含 $k$ 个点。
每次修改的时候跳链表修改前 $k$ 个位置。
不存在点的位置的 $f$ 等于向后第一个存在点的位置的 $f$ 值。所以维护一下 $\sum f_i(i-\textrm{las}_i)$,其中 $i$ 在链表内,$\textrm{las}_i$ 表示链表的上一个元素。
# [623E Transforming Sequence](https://codeforces.com/problemset/problem/623/E)
对于一个整数序列 $\{a_1, a_2, \ldots, a_n\}$,我们定义它的变换为 $\{b_1, b_2, \ldots, b_n\}$,其中 $b_i = a_1 | a_2 | \ldots | a_i$,其中 $|$ 表示二进制按位或运算。
现在求有多少个长为 $n$ 的序列 $a$,满足 $1\leq a_i \leq 2^k - 1$,使得它的变换 $b$ 是**严格单调递增**的,对 $10^9+7$ 取模。
$1\leq n \leq 10^{18}$,$1\leq k \leq 3 \times 10^4$。
***
[评测链接](https://codeforces.com/contest/623/submission/94253757)
首先,我们把题意转化为有 $n$ 个集合,$k$ 种元素。每个集合里必须有新的元素,每个集合之前的集合元素可以选择加入或不加入,求不同的集合数。
显然 $n > k$ 时答案为 $0$。
以下默认已特判此情况。
我们考虑递推答案。设 $f_{i, j}$ 表示前 $i$ 个集合,出现了前 $j$ 种元素的方案数(我们假设元素已经从 $1$ 至 $k$ 标号)。则答案为 $\sum _{i=n}^k f_{n, i}\times A_k^i$,其中 $A_k^i$ 为排列数,表示不同的标号方案。
则有
$$f_{i, j}=\sum_{l=i-1}^{j-1} \frac{f_{i-1, l}\times 2^l}{(j-l)!}$$
边界为 $f_{0, 0}=1$。
其中因为已有 $l$ 种元素,每种都可以选或不选,所以乘 $2^l$。因为单个集合里元素由排列关系变为组合关系,所以需要除以 $(j-k)!$。
由于转移都是 $i - 1 \to i$,我们可以除去第一维。则有
$$f_j=\sum_{l=i-1}^{j-1} \frac{f_l\times 2^l}{(j-l)!}$$
方便起见,我们将 $2^l$ 乘入状态,即 $f_i$ 表示出现了 $i$ 种元素的方案数乘 $2^i$ 的值。则有
$$f_j=2^j\sum_{l=i-1}^{j-1} \frac{f_l}{(j-l)!}$$
最终答案为
$$\sum _{i=n}^k \frac{f_{n, i}\times A_k^i}{2^i}$$
我们观察递推式,发现后面是卷积的形式,我们可以用多项式乘法将其时间复杂度优化至 $O(nk\log k)$。
我们现在考虑如何加速这一过程。发现我们将重复的操作进行了 $n$ 遍,能否进行倍增呢?发现 $2^i$ 难以处理。
我们设 $g_i=\frac 1{i!}$,则有 $f'_i=2^i \sum_j f_jg_{i-j}$。其中 $\ast$ 表示卷积。
$$f'=\sum_i 2^i(\sum_j f_jg_{i-j})x^i=\sum_i (\sum_j f_jg_{i-j})(2x)^i=\sum_i f(2x)\ast g(2x)$$
进行迭代,不难发现最终答案为 $\prod_{i=1}^n g(2^ix)$。这个式子可以进行倍增,设 $P_n(x) =\prod_{i=1}^n g(2^ix)$,则有 $P_{2n}(x)=P_n(x) \ast P_n(2^nx)$。
时间复杂度:$O((n+k)\log n\log k)$。
注意模数为 $10^9+7$,所以还需要一个任意模数 NTT。
# [613E Puzzle Lover](https://codeforces.com/problemset/problem/613/E)
给定一个 $2 \times n$ 的矩阵,每个位置上有一个小写字母。
有一个长度为 $k$ 的小写字符串 $w$,询问矩阵中有多少条有向路径满足以下条件:
- 路径上的字母连起来恰好为 $w$。
- 不多次经过同一个位置。
- 只能向上下左右四个方向走。
$n,k \le 2 \times 10^3$,答案对 $10^9+7$ 取模。
***
[评测链接](https://codeforces.com/contest/613/submission/106180672)
路径应该形如

其中,第一段和第三段是折回来的,第二段是上下交替的。
我们可以对于每个位置,求出可以匹配的前缀/后缀有哪些。之后我们只用考虑第二段匹配中间。
设 $p_{i, j, k}$ 表示到位置 $(i, j)$,匹配了前 $k$ 位的方案数。
这样好像不太好处理同一列的两个元素的关系。
所以设 $p_{1, i, j, k}$ 表示到位置 $(i, j)$,匹配 $k$,还没走同一列另一个位置的方案数,$p_{2, i, j, k}$ 表示已经走了。
# [611H New Year and Forgotten Tree](https://codeforces.com/problemset/problem/611/H)
有一棵 $n$ 个节点的树,节点编号为 $1 \sim n$。
记录这棵树的方式是记录下每条边连接的两点的编号。
现在,你不知道这些编号具体是多少,你只知道它们在十进制下的位数。
请你构造出一棵满足要求的树,或判断没有满足要求的树。
$n \le 2 \times 10^5$。
***
[评测链接](https://codeforces.com/contest/611/submission/103134721)
对于每一种位数,我们设立一个关键点,关键点之间连成一棵树,所有其他的连边,我们都使用关键点连向新点。
但是有两种情况:$x$ 新点连向 $y$ 关键点,$y$ 新点连向 $x$ 关键点。这是一个匹配的模型。
关键点和关键点的连边,我们可以暴力枚举所有的树型,这样的复杂度是 $O(m^{m-2})$ 的($m$ 是位数,最大为 $5$)。
之后我们用网络流做一个匹配即可。
# [603E Pastoral Oddities](https://codeforces.com/problemset/problem/603/E)
给定一张 $n$ 个点的无向图,初始没有边。
依次加入 $m$ 条带权的边,每次加入后询问是否存在一个边集,满足每个点的度数均为奇数。
若存在,则还需要最小化边集中的最大边权。
$n \le 10^5$,$m \le 3 \times 10^5$。
***
[评测链接](https://codeforces.com/contest/603/submission/70271946)
存在合法边集的充分必要条件是不存在一个大小为奇数的连通块。
必要性:一条边贡献度数和为 $2$,若大小为奇数,那一定存在一个点度数为偶数。
充分性:大小为偶数的连通块,我们可以求出其一棵生成树。生成树必定存在完美匹配。
如何最小化最大边权,我们使用类似维护动态最小生成树的方法,维护合法图。
每当加入一条边后,考虑删除边集中最大的边,如果删除后仍合法就可以删除。
LCT 维护即可。
# [587D Duff in Mafia](https://codeforces.com/problemset/problem/587/D)
给定一张 $n$ 个点 $m$ 条边的无向图,每条边有一个颜色 $c$ 和权值 $t$。
你要选出一些边,使得它们是一个**匹配**,同时剩下的边每种颜色也是一个**匹配**。
同时,你要最小化选出的边的最大权值。
$n,m \le 5 \times 10^4$。
***
[评测链接](https://codeforces.com/contest/587/submission/98647100)
2-SAT 优化建图练习题。
先二分答案,假设大于这个答案的都不能选,其他的边随意。
设 $x$ 表示选,$x'$ 表示不选。于是我们需要连三种边。
* 对于不能选的边,$x \to x'$。
* 小于二分值的,对于每个点的出边 $i, j$($i \neq j$),$x_i \to x_j'$。
* 其他的边,对于每个点,同颜色的 $i, j$($i \neq j$),$x_i \to x'_j$。
这样连边是 $O(n^2)$ 的。
发现限制形如若干个点只能选一个。前缀优化建图即可。
具体地,设 $s_i$ 表示前 $i$ 个有没有选。则有:
* $x_i \to s_i, s_i \to s_{i+1}$,表示 $s$ 是 $x$ 的前缀和。
* $s_i \to x_{i+1}'$,表示限制只能选一个。
# [585F Digits of Number Pi](https://codeforces.com/problemset/problem/585/F)
给定长度为 $n$ 的数字串 $s$ 和长度为 $d$ 的不含前导零的数字串 $x,y(x \le y)$。
求**存在长度至少为 $\left\lfloor\frac{d}{2}\right\rfloor$ 的子串是 $s$ 的子串**的数字串 $t \in [x,y]$ 的数量。
$n \le 10^3$,$d \le 50$。
***
[评测链接](https://codeforces.com/contest/585/submission/66206508)
平凡题。
把所有 $\lfloor \frac d2 \rfloor$ 的子串拉出来建 AC 自动机。
然后数位 dp。
# [582E Boolean Function](https://codeforces.com/problemset/problem/582/E)
$A,B,C,D,a,b,c,d$ 为八个布尔「变量」,其中小写字母的值等于对应大写字母的值取反。
$\&,|$ 为两个布尔「操作符」。
布尔「表达式」为一个「变量」,或通过「操作符」连接起来的两个「表达式」。
布尔「函数」$f(A,B,C,D)$ 为一个布尔「表达式」。
给定一个可能缺少某些「变量」和「操作符」(用 `?` 代替)的「函数」$s$,并给出 $n$ 个**函数在 $A,B,C,D$ 确定时**的值。
求可能的「函数」个数。
$|s|\le 500$,$n \le 16$,答案对 $10^9+7$ 取模。
***
[评测链接](https://codeforces.com/contest/582/submission/93602702)
先建出表达式树。
设 $f_{u, s}$ 表示 $u$ 号点,把 $f(A, B, C, D)=1$ 的下标 $\overline{ABCD}_{(2)}$ 设为 $1$ 的方案数。可以发现 $s$ 有 $2^{16}$ 种。
实际上是 dp 套 dp 类似物。
# [582D Number of Binominal Coefficients](https://codeforces.com/problemset/problem/582/D)
给定质数 $p$ 和整数 $\alpha,A$,求满足 $0 \le k \le n \le A$ 且 $p^{\alpha}|\binom nk$ 的数对 $(n,k)$ 的个数。
$p,\alpha \le 10^9$,$A < 10^{1000}$,答案对 $10^9+7$ 取模。
***
[评测链接](https://codeforces.com/contest/582/submission/92394950)
经典题。
库默尔定理:质数 $p$ 进制下 $a+b$ 的进位次数等于 $\binom{a+b}a$ 的标准分解式中 $p$ 的次数。
证明:$\binom {a+b}a=\frac {(a+b)!}{a!b!}$,$n!$ 中 $p$ 的次数为 $\log_p n+\log_p \frac np + \log_p \frac n{p^2}+\ldots$,进位一次对应着次数加一。
所以我们只需要求 $0 \leq a+b \leq s$,$a+b$ 在 $p$ 进制下进位次数至少为 $c$ 的方案数。
数位 dp 即可。
# [578F Mirror Box](https://codeforces.com/problemset/problem/578/F)
在一个 $n \times m$ 的网格中,每个格子里都有一个呈 `\` 或 `/` 状的镜子。
一个合法的网格需要满足**从任意一个边界段垂直射进网格中,光线会从相邻的边界段射出**,同时**网格中的每一段都被至少一条光线穿透**。
现在网格中有 $k$ 个位置的镜子形状不确定,求有多少种合法的网格。
$n,m \le 100$,$k \le 200$,答案对质数 $p$ 取模。
***
[评测链接](https://codeforces.com/contest/578/submission/95703770)
我们把 $i+j$ 为奇数的点 $(i, j)$ 染成黑色,则任何一棵黑色点构成的生成树都是合法的。
同理 $i+j$ 为偶数也行。
跑两遍矩阵树定理。
# [576E Painting Edges](https://codeforces.com/problemset/problem/576/E)
给定一张 $n$ 个点 $m$ 条边的无向图。
一共有 $k$ 种颜色,一开始,每条边都没有颜色。
定义**合法状态**为仅保留**染成 $k$ 种颜色中的任何一种颜色**的边,图都是一张二分图。
有 $q$ 次操作,第 $i$ 次操作将第 $e_i$ 条边的颜色染成 $c_i$。
但并不是每次操作都会被**执行**,只有当执行后仍然合法,才会执行本次操作。
你需要判断每次操作是否会被执行。
$n,m,q \le 5 \times 10^5$,$k \le 50$。
***
[评测链接](https://codeforces.com/contest/576/submission/74688798)
线段树分治,带权并查集。
# [573D Bear and Cavalry](https://codeforces.com/problemset/problem/573/D)
有 $n$ 个人和 $n$ 匹马,第 $i$ 个人对应第 $i$ 匹马。第 $i$ 个人能力值 $w_i$,第 $i$ 匹马能力值 $h_i$,第 $i$ 个人骑第 $j$ 匹马的总能力值为 $w_i\times h_j$,整个军队的总能力值为 $\sum w_i\times h_j$(一个人只能骑一匹马,一匹马只能被一个人骑)。有一个要求:每个人都不能骑自己对应的马。让你制定骑马方案,使得整个军队的总能力值最大。现在有 $q$ 个操作,每次给出 $a,b$,交换 $a$ 和 $b$ 对应的马。每次操作后你都需要输出最大的总能力值。
$n \leq 3 \times 10^4$。
***
[评测链接](https://codeforces.com/contest/573/submission/97210917)
我们设 $\mathrm{ban}_i$ 表示 $i$ 不能匹配的马。
则有结论:我们把 $w, h$ 排序后,每个人 $i$ 匹配的马必定在 $[i-2, i+2]$ 中。
证明:我们把每个人当作一个点放在左边,每匹马当作一个点放在右边。根据排序不等式,$a_1 \leq a_2, b_1 \leq b_2$ 则 $a_1b_1+a_2b_2 \geq a_2b_1+a_1b_2$。我们把匹配的人和马连边,则不交叉比交叉的权值更大,或者说,逆序对往更少调整,权值更大。
那么,我们考虑一组匹配 $(i, i + 3)$。
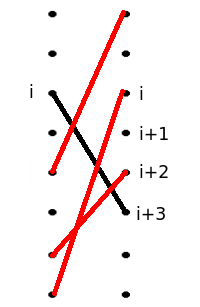
此时,左下比右下多了三个点,所以至少有三组匹配跨越了 $(i, i + 3)$(红线)。红线中可能有一匹马为 $\mathrm{ban_i}$,我们无法交换它和 $(i, i+3)$;有一个人 $j$ 的 $\mathrm{ban}$ 为 $i + 3$,我们也无法交换它和 $(i, i + 3)$。但这样总会剩下一组可以交换。交换后,逆序对数变少了,显然权值更大。所以不会存在 $(i, i+3)$ 的匹配。$(i, i-3)$ 同理。
同时,我们也可以通过交换的过程得到一条性质:如果前 $i$ 个人和前 $i$ 匹马匹配完成,那么存在 $k\leq 3$,使得 $[i, i+k]$ 中的人和马匹配。和上文一样可以用反证法,得到必然存在一种交换方式。
所以,我们设 $f_i$ 表示前 $i$ 个人和前 $i$ 匹马匹配完成的最大权值,只从 $f_{i-3}, f_{i-2}, f_{i-1}$ 转移。
由于有修改,我们直接用动态 dp 就好。
# [571D Campus](https://codeforces.com/problemset/problem/571/D)
有一个长度为 $n$ 的序列,初始全为 $0$。
有两类对下标的集合,初始时每一类各有 $n$ 个集合,编号为 $i$ 的集合里有下标 $i$。
一共有 $m$ 个操作,操作有五种:
1. `U x y` 将第一类编号为 $y$ 的集合合并到编号为 $x$ 的集合里。
2. `M x y` 将第二类编号为 $y$ 的集合合并到编号为 $x$ 的集合里。
3. `A x` 将第一类编号为 $x$ 的集合中的所有下标在序列中对应的数加上 $x$ 的集合大小。
4. `Z x` 将第二类编号为 $x$ 的集合中的所有下标在序列中对应的数设为 $0$。
5. `Q x` 询问序列中下标为 $x$ 的位置上的数。
$n,m \le 5 \times 10^5$。
***
[评测链接](https://codeforces.com/contest/571/submission/87390356)
对于每次询问,我们求出其最后一次被赋值的时间,之后就是查询在这个时间之后的,修改操作的和。
用 kruskal 重构树维护合并,加操作变为子树加。
离线后先求出被赋值的时间,之后用树状数组维护即可。
# [568E Longest Increasing Subsequence](https://codeforces.com/problemset/problem/568/E)
给定一个长度为 $n$ 的有 $k$ 个空缺的序列。
你有 $m$ 个数可以用于填补空缺。
要求最大化最长上升子序列的长度。
$n, m \le 10^5$,$k \le 10^3$。
***
[评测链接](https://codeforces.com/contest/568/submission/91757469)
设 $f_i$ 表示长度为 $i$ 的上升子序列最后一项的最小值。
如果不是空缺,那 `lower_bound`。
如果是,那枚举放的是什么,`lower_bound`,但这样多个 $\log$,所以从小到大枚举放的是什么,用指针扫过去。
之后倒着填回去就行。
# [566E Restoring Map](https://codeforces.com/problemset/problem/566/E)
有一棵 $n$ 个点的树,你不知道这棵树的边是怎么连的。
你得到了 $n$ 条关于每个点信息,每条信息记录了距离某一个点 $\le 2$ 的所有点。
但你不知道每条信息具体是哪个点的。
你需要构造一棵满足这些信息的树。
$n \le 10^3$。
***
[评测链接](https://codeforces.com/contest/566/submission/111746326)
考虑一条长度为 $4$ 的链,边上两个点的集合的交为中间两个点。我们可以以此获得非叶结点间的连边。并且这是充要条件。也就是说只要两个集合的交的大小为 $2$,那么两个点之间必然有一条边。
接下来考虑叶子问题。我们首先已经知道哪些结点为叶子,并且我们能找出它对应的连边集合。对于叶子 $u$,包含 $u$ 的所有集合中大小最小的一个为 $u$ 对应的连边集合。
之后我们用已经获得的非叶节点的连接信息判断出每个叶子对应的父亲。我们把叶子节点的连边集合去掉所有叶子,新的集合就是 $u$ 的父亲的邻接集合,所以先预处理出每个点的邻接集合即可。
$O(\frac {n^3}\omega)$。
# [566C Logistical Questions](https://codeforces.com/problemset/problem/566/C)
一棵 $n$ 个节点的树,点有点权,边有边权。
两点间的距离定义为两点间边权和的 $\frac 32$ 次方。
求这棵树的带权重心。
$n \le 2 \times 10^5$。
***
[评测链接](https://codeforces.com/contest/566/submission/92542442)
$f(x)=x^{\frac 32}$ 是凸函数。
我们可以得知任意一点到重心的路径上,权值和是递减的。
那么我们可以求出从 $u$ 到 $v$ 的权值和的差,如果是正的那就走到 $v$。
但是一次计算的复杂度是 $O(n)$ 的。
所以我们使用点分树,这样只用走 $O(\log n)$ 次。
# [553E Kyoya and Train](https://codeforces.com/problemset/problem/553/E)
给定一张 $n$ 个点 $m$ 条边的无重边无自环的有向图,你要从 $1$ 号点到 $n$ 号点去。
如果你在 $t$ 时刻之后到达 $n$ 号点,你要交 $x$ 元的罚款。
每条边从 $a_i$ 到 $b_i$,走过它需要花费 $c_i$ 元,多次走过同一条边需要多次花费。
走过每条边所需的时间是随机的,对于 $k \in [1,t]$,$\frac{p_{i,k}}{10^5}$ 表示走过第 $i$ 条边需要时间 $k$ 的概率。因此如果多次走过同一条边,所需的时间也可能不同。
你希望花费尽可能少的钱(花费与罚款之和)到达 $n$ 号点,因此每到达一个点,你可能会更改原有的计划。
求在最优决策下,你期望花费的钱数。
$n \le 50$,$m \le 100$,$t \le 2 \times 10^4$,$x,c_i \le 10^6$,$\sum_{k=1}^t p_{i,k} = 10^5$,答案精度误差 $\le 10^{-6}$。
***
[评测链接](https://codeforces.com/contest/553/submission/116903749)
由于有罚款,我们需要在状态中记录时间信息。不过也只用记录到 $t$。
设 $f_{i, j}$ 表示 $i$ 号点走到终点,目前的时间为 $j$ 的期望最小花费。
$$f_{u, j}=\begin{cases}\textrm{dis}(u, n)+x& j =t\\ 0&u=n, j\neq t\\ \min(\sum_{l=1}^tp_lf_{v, l+j}+c)\end{cases}$$
这样复杂度是 $O(mt^2)$ 的。
考虑分治 FFT。
设 $g_{i, j}$ 表示在时间 $j$ 走第 $i$ 条边的期望最小花费。
那分治 FFT 便是 $f_{*, [mid, r]}$ 向 $g_{*, [l, mid]}$ 贡献,$g$ 可以直接推出 $f$。
$O(mt\log^2t)$。
# [538H Summer Dichotomy](https://codeforces.com/problemset/problem/538/H)
有 $T$ 名学生,你要从中选出至少 $t$ 人,并将选出的人分成两组,可以有某一组是空的。
有 $n$ 名老师,每名老师要被分配到两个小组之一,对于第 $i$ 名老师,要求所在的小组中的学生人数 $\in [l_i, r_i]$。
此外,有 $m$ 对老师不能在同一个小组中。
你需要判断能否满足所有要求,如果可以,请给出一种方案。
$t \le T \le 10^9$,$n,m \le 10^5$。
***
[评测链接](https://codeforces.com/contest/538/submission/97207782)
特判全部老师有交的情况。
设第一组放较大的一些老师,第二组放较小的一些老师。
第一组的下界为 $\max{l}$,第二组的上界为 $\min r$。
当他俩的和过大时,第二组减小。过小时,第一组增大。发现第一组减小,第二组增大都是无意义的。
然后跑一个二分图染色,完了。
# [538G Berserk Robot](https://codeforces.com/problemset/problem/538/G)
有一个机器人,第 $0$ 秒时在 $(0,0)$ 位置。
机器人会循环执行一个长度为 $l$ 的指令序列,每秒执行一个指令。
指令有 `ULDR` 四种,分别代表向上/左/下/右移动一格。
你不知道这个指令序列具体是什么,但是你知道 $n$ 条信息,第 $i$ 条信息为「第 $t_i$ 秒时机器人在 $(x_i,y_i)$」,保证 $t$ 递增。
你需要构造一个满足这些信息的指令序列,或判断不存在。
$n \le 2 \times 10^5$,$l \le 2 \times 10^6$,$t_i,|x_i|,|y_i| \le 10^{18}$。
***
[评测链接](https://codeforces.com/contest/538/submission/118242376)
转切比雪夫。
于是对于每一维,都有若干个限制形如:$\lfloor\frac tl\rfloor s_l+s_{t \mod l}=x$。其中 $s$ 为序列的前缀和。
发现这样还是不好处理,由于有可能存在 $j$ 使得 $s_l < s_j$。所以我们再把坐标转化一下变为 $(\frac{x_i+y_i+t}2, \frac {-x+y_i+t}2)$,也就是把 $t$ 放进去。这样每次走的是 $0/+1$。故有 $i>j$ 时 $0 \leq s_i-s_j \leq i-j$。如果不考虑奇偶性,这是存在 $s$ 序列的充要条件。
我们差分两条信息,得到:
$x \leq ks_l=x+(s_a-s_b) \leq x+(a-b)
解一下 s_l 的解集就好,之后随便构造一下就完了。
533D Landmarks
有 n+2 根柱子支撑着一栋老房子。这些柱子位于坐标为 x_0,x_1,x_2,\cdots ,x_{n+1} 的点上。对于位于 x_1\cdots x_n 的柱子,我们知道它的承重系数 d_i 。位于 x_0,x_{n+1} 两个位置的柱子的承重系数可以认为是 +\infty 。
对于位于 x_i 的柱子,需要承重的部分为它到两边柱子距离的一半,即 [\frac {x_{i-1}+x_i}2,\frac {x_i+x_{i+1}}2] 。当该长度超过 d_i 时该柱子会坍塌。因此,会不断地有柱子坍塌。而位于 x_0 和 x_{n+1} 的柱子不会坍塌。
当只剩下位于 x_0 和 x_{n+1} 的柱子时,这栋老房子将会坍塌。
现在要求你往建筑中间加一根柱子,使得房子不会坍塌。可以在原有柱子的位置替换掉原有的柱子。求房子不坍塌的情况下,这根新加的柱子的承重系数的最小值。
***
[评测链接](https://codeforces.com/contest/533/submission/97518953)
考虑最终稳定状态。发现新柱子只会救助相邻的俩柱子。其他的原样。
我们设 $f_i$ 表示前 $i$ 个柱子能够稳定的最靠右的是哪个。单调栈转移一下。
倒着再做一遍。
推推式子发现是个二维“数“点问题(一维区间限制,一维找 $\min$)。完了。
# [526G Spiders Evil Plan](https://codeforces.com/problemset/problem/526/G)
给定一棵 $n$ 个节点的无根树,每条边有边权。
有 $q$ 次询问,每次询问给出 $x,y$,你需要选择 $y$ 条树上的路径,使这些路径形成一个包含 $x$ 的连通块,且连通块中包含的边权和最大。
$n, q \le 10^5$,强制在线。
***
[评测链接](https://codeforces.com/contest/526/submission/93159484)
我们可以证明,对于一棵 $2k$ 个叶子的树,我们可以用 $k$ 条路径包含整棵树。
调整法。首先肯定路径端点都是叶子更优。
假设在一种覆盖方案中,有一条路径无法被覆盖。他把树分成了两个连通块。我们从这两个连通块中各选出一条路径 $(a, b), (c, d)$,改为 $(a, c), (b, d)$,发现不仅覆盖了原来的路径,也覆盖了这一条。
它的另一种形式:我们选择了 $2k$ 个叶子,我们可以用 $k$ 条路经覆盖他们的虚树。
很显然地,直径端点一定会被选(当 $k$ 足够大的情况下)。我们可以以他为根建立虚树。
那么考虑虚树的建立过程,每次加入一个点的贡献应该为以其开始向上直到原虚树的一段路径。
如果我们使用长链剖分,就能保证每次加入的贡献都是最大的。这样我们可以对于每个 $k$ 都求出答案。
再考虑强制要求加入 $x$ 的情况。要么我们删去贡献最小的,要么将 $x$ 向上找到的第一条路径调整至 $x$。讨论一下即可。
# [526F Pudding Monsters](https://codeforces.com/problemset/problem/526/F)
给定一个 $n \times n$ 的棋盘,其中有 $n$ 个棋子,每行每列恰好有一个棋子。
求有多少个 $k \times k$ 的子棋盘中恰好有 $k$ 个棋子。
$n \le 3 \times 10^5$。
***
[评测链接](https://codeforces.com/contest/526/submission/68340358)
在一维上对于一个区间 $[l_1, l_1+k)$,至多有一个第二维的 $[l_2, l_2+k)$ 满足条件。满足条件当且仅当 $\max-\min=k$。
第一维序列分治,完了。
# [516E Drazil and His Happy Friends](https://codeforces.com/problemset/problem/516/E)
有 $n$ 个男生 $m$ 个女生,编号分别为 $0 \sim n - 1$ 和 $0 \sim m - 1$。
有 $b$ 个男生和 $g$ 个女生是快乐的,其他人是不快乐的。
在第 $i$ 天,编号为 $i \bmod n$ 的男生和编号为 $i \bmod m$ 的女生会一起玩。
如果他们俩中有一个人是快乐的,则另一个人也会变快乐。
求至少要多少天所有人都会变快乐,或者判断不可能所有人都变快乐。
$n,m \le 10^9$,$b,g \le 10^5$。
***
[评测链接](https://codeforces.com/contest/516/submission/98358463)
$\gcd(n, m)$ 分组,每组不干涉。
同组每两个都会一起玩。所以必定有解。只用算时间。
如果男生 $i$ 快乐,那么男生 $i+km \mod n$ 会在 $km$ 天后快乐。在这个环上,推推就发现答案只用考虑相邻两个快乐的人差的最大值。女生同理。
# [513G3 Inversions problem](https://codeforces.com/contest/513/problem/G3)
有长度 $n$ 的 $n$ 阶排列 $p_i$,$k$ 次操作,每次等概率反转一个区间,求最后逆序对的期望。误差 $<10^{-9}$ 即可。
$n \le100 ,k\le10^9$。
***
[评测链接](https://codeforces.com/contest/513/submission/99006603)
看到逆序对期望想到拆贡献。
设 $f_{a, b}$ 表示位置 $a, b$ 产生的贡献。枚举每次反转的区间。复杂度 $O(kn^4)
发现可以前缀和优化,做到 O(kn^2) 。
发现 f 在 k \to +\infty 时显然是收敛的。一测发现 k\leftarrow \min(k, 1000) 已经满足精度要求了。这种递推题不取模一般都要留意一下这种无趣的突破点。
506E Mr. Kitayuta's Gift
给定一个小写字符串 s 和一个正整数 n 。
要求在 s 中插入恰好 n 个小写字符使其回文的方案数。
***
[评测链接](https://codeforces.com/contest/506/submission/93633928)
考虑插入字符判断是否回文的自动机结构。