【数学】三边相等的四边形与60度角
A_Đark_Horcrux
·
2020-02-22 22:55:53
·
个人记录
\Huge\textsf{三边相等的四边形与60}\degree\textsf{角}
解决题目的关键是:
看到两个已知角的和是60\degree 的倍数,
就可以构造正三角形。
直接上题!
\Large\texttt{例<1>}
如图,AB = BC = CD,\;\angle C=80\degree ,\;\angle B=160\degree , 求\angle A.
此题在我的这篇文章中已经介绍过了,但我还是把过程再来一遍。
解:
以CD 为边向上作正三角形CED ,连接AE ,则 AB = BC = CD = CE = ED
\angle BCE = \angle BCD - \angle ECD = 80\degree - 60\degree = 20\degree = 180\degree - \angle B ,\;\therefore AB \parallel CE
又\because AB = BC = CE,\;\therefore \; 四边形ABCE 为菱形,\therefore AE = …… = ED .
\angle AED = 360\degree - \angle AEC - \angle CED = 360\degree - 160\degree - 60\degree = 140\degree
\therefore \angle EAD = \angle EDA = (180\degree - 140\degree)/2 = 20\degree
\therefore \angle BAD = \angle BAE + \angle EAD = 20\degree + 20\degree = 40\degree .
\Large\texttt{例<2>}
如图,AB = BC = CD ,\;\angle B = 150\degree , \angle C = 90\degree , 求\angle A .
解:还是底边造正三角形。
同理ED = EC = DC = EA = AB = BC ,\;\therefore ABCE 为菱形,
\therefore \angle AEC = \angle B = 150\degree ,\;\angle EAB = \angle ECB = 30\degree .
\because \angle AEC = 150\degree , \;\angle DEC = 60\degree ,\;\therefore \angle AED = 150\degree ,
又\because EA = ED,\;\therefore \angle EAD = \angle EDA = 15\degree .
\therefore \angle A = \angle DAE + \angle BAE = 15\degree + 30\degree = 45\degree .
\Large\texttt{例<3>}
如图,AB = BC = CD ,\;\angle C = 170\degree , \angle B = 70\degree , 求\angle D .
我猜我题目没念完你都算出来了。
好,有了三题,我们已经可以对这一种情况总结出通式了:
在凸四边形ABCD 中,AB=BC=CD,\angle B +\angle C = 240\degree , 则剩下两个角较小的一个为\frac{1}{2} \angle B.
\large\textsf{小拓展!}
第二题其实有一种更简单的做法:
如图,往左构造正方形DCBE ,连接EA.
$\therefore \angle AED = 60\degree + 90\degree = 150\degree ,\;$又因为$AE = AD ,\;\therefore \angle EAD = \angle EDA = 15\degree ,
\therefore \angle DAB = \angle EAB - \angle EAD = 60\degree - 15\degree = 45\degree .
然而不通用pwp
但这也只是一种情况……
\Large\texttt{例<4>}
如图,CA = AB = BD ,\;\angle A = 20\degree , \angle B = 100\degree , 求\angle D .
解:继续底边造等边三角形。造完以后,连接EC、ED。
易得AE = BE = AB = AC = BD ,\;\angle EAC = \angle EAB - \angle CAB = 40\degree ,
\therefore \angle ACB = \angle ABC = 80\degree ,\;\angle ACE = \angle AEC = 70\degree ,\angle ECB = \angle ACE + \angle ACB = 150\degree .
\angle DBE = \angle ABD - \angle ABE = 40\degree ,\;\angle DBC = \angle ABD - \angle ABC = 20 \degree ,\;\therefore \angle DBC = \angle EBC = 20\degree
又\because EB = DB ,\;CB 为公共边,\therefore \triangle CBE \cong \triangle CBD \;(SAS)
\therefore \angle DCB = \angle ECB = 150\degree ,\;\angle ECD = 360\degree - \angle DCB - \angle ECB =60\degree .
又\because EC = DC ,\;\therefore \triangle ECD 为等边三角形,\;\therefore \angle EDC = 60\degree .
\therefore \angle CDB = \angle EDB - \angle EDC = 10\degree .
\Large\texttt{例<5>}
如图,AB = BC = CD ,\;\angle C = 10\degree , \angle B = 110\degree , 求\angle D .
我都懒得描述辅助线了。你们猜猜辅助线是什么?
解:还是底边造等边三角形。造完以后,仍然连接EA、ED。
同理可以得\angle EDB = 150\degree ,\;\therefore \triangle EDB \cong \triangle ADB \;(SAS),\;
\triangle ECD $为等边三角形$,\;\angle DAB = \angle EAB - \angle EAD = 5\degree .
于是我们出了第二个通式:
在凹四边形ABCD 中,AB=BC=CD,\angle B +\angle C = 120\degree , 则剩下的锐角为\frac{1}{2} \angle C.
看累了?来张图洗洗眼睛吧awa
不急,我们没完呢!
\Large\texttt{例<5>}
如图,AB = BC = CD ,\;\angle C = 70\degree , \angle B = 50\degree , 求\angle D .
你体验过一招打遍天下的快感嘛?
解:依然是底边造等边三角形。造完以后,连接EC。
则AE = BE = AB = BC = CD ,\;\angle EBC = \angle EBA - \angle CBA = 10\degree
\therefore \angle AFB = \angle FEB + \angle FBE = 60\degree + 10\degree = 70\degree = \angle DCB ,\;\therefore CD \parallel EA ,\;
\angle BCE = \angle BEC = 85\degree ,\;\therefore \angle DCE = 155\degree .
又\because CD = EA ,\;\therefore CDAE\; 是平行四边形!
\therefore \angle D +\angle ACE = 180\degree ,\;\angle D = 25\degree !
\Large\texttt{例<6>}
如图,AB = BC = CD ,\;\angle C = 80\degree , \angle B = 40\degree , 求\angle D .
在洛谷,享受切题的乐趣!
解:仍然是底边造等边三角形。造完以后,连接EC。
同理得\angle DCE = 160\degree ,\;DCEA \; 为平行四边形,\angle D = 180\degree - \angle DCE = 20\degree .
出现了!第三个通式!
在凹四边形ABCD 中,AB=BC=CD,\angle B +\angle C = 120\degree , 则剩下的锐角为\frac{1}{2} \angle B.
我们还可以继续!
\Large\texttt{例<7>}
如图,AB = BC = CD ,\;E 为AC 、BD 交点,\angle AEB = 60\degree ,\; 求证:EA = ED.
依旧是造正三角形,只不过这题如何构造比较不容易想到。
\large\texttt{法<1>}
向右构造正三角形AEF ,易得E,B,F 共线。
设\angle EAB = \angle ECB = \alpha ,\;\angle BDC = \angle DBC = \beta.
在\triangle BEC 中,\angle ECB + \angle EBC = \angle AEB ,即\alpha + \beta = \angle AEB = 60\degree ;
而\angle EAB + \angle FAB = \angle EAF ,即\alpha + \angle BAF = 60\degree ,\;\therefore \angle BAF = \beta .
\angle FAB = \angle EDC =\beta ,\;BA = CD ,\; \angle F = \angle DEC = 60\degree ,\; \therefore \triangle FAB \cong \triangle EDC ,
---
$$ $$
$$\large\texttt{法<2>}$$
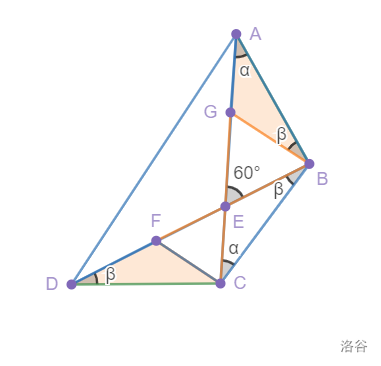
我这次向内构造两个正三角形$\triangle CEF$和$\triangle BEG ,
同理倒角,可得 \triangle GAB \cong \triangle FCD ,
其实这里还有一对全等$\triangle DFC \cong \triangle BEC $,但是没用上。
---
$$ $$
$$\large\texttt{小拓展!}$$
脱离正三角形了哦qwq
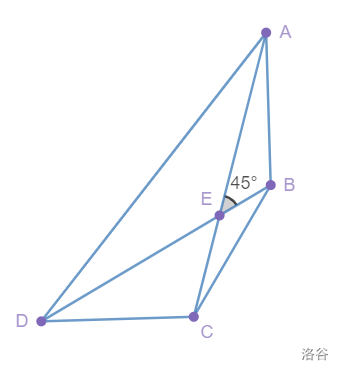
如图,$AB = BC = CD ,\;E$为$AC$、$BD$交点,$\angle AEB = 45\degree ,\;$求证:$BD = \sqrt{2}AE.
你一看到六十度变成了45度,该构造啥?
其实把正三角形换成等腰直角三角形就可以啦awa
解:向右构造等腰直角三角形AEF ,易得E,B,F 共线;作GC\perp BD 于D .
设\angle EAB = \angle ECB = \alpha ,\;\angle BDC = \angle DBC = \beta.
在\triangle BEC 中,\angle ECB + \angle EBC = \angle AEB ,即\alpha + \beta = \angle AEB = 45\degree ;
而\angle EAB + \angle FAB = \angle EAF ,即\alpha + \angle BAF = 45\degree ,\;\therefore \angle BAF = \beta .
\angle FAB = \angle GBC =\beta ,\;BA = CB ,\; \angle F = \angle CGB = 90\degree ,\; \therefore \triangle FAB \cong \triangle GBC ,\;\therefore AF = BG.
由于三线合一, DG = BG = AF.
另一种方法同理。
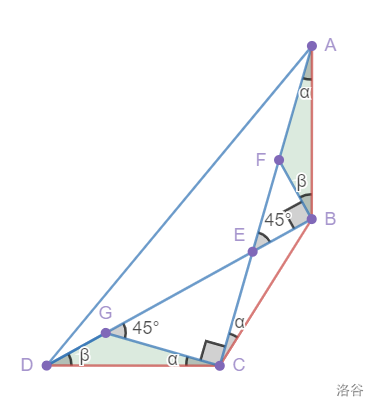
这里没用上的全等就有用了!
$\triangle DGC \cong \triangle BEC ,\;\therefore BE = DG,
\therefore AE = AF + FE = GC + \sqrt{2}BE = \frac{\sqrt{2}}{2}(GE + 2BE) = \frac{\sqrt{2}}{2} BD .
\huge\textsf{总结}
\small\texttt{Summary!}
总结起来就是遇到两个角和是60\degree 的倍数的时候就作正三角形吧。
为什么是60\degree 的倍数的时候作正三角形,我猜这样才能和正三角形挂钩。
至于结论为什么都是二倍角,就不得而知了,可能只是巧合。
附录:
1.画图软件:Desmos
( 几何区 )
2.参考资料:暂时没在网络上找到相应资料
3.转载请注明出处 \tiny\textbf{(虽然应该不会有人来抄我这个小菜鸡的文章XD)}