一些高联二试模拟题
Scrutiny
·
·
个人记录
收录一些全国高中数学联赛二试模拟题,题目不一定是我出的,但一定是我汇集成一张模拟卷的,如果对题目分数编排有异议,请在评论区提出(
一些题目会带有【原创】标签,表示是我自己出的题,不排除 idea 重复的可能性。
每篇模拟题都会给出我的评价。
二试模拟Ⅰ
我的评价:几何题高于近年二试几何难度;其余题目难度均明显低于近年高联二试平均难度。总体较为简单,适合萌新练习、高手热身。
1.(40')
如图,在 \odot O 上有三点 B,C,D,在圆上任取一点 A。
过 C 点作 AC 的垂线,过 D 点作 AB 的垂线,二者交于 E。若 DB=DC,求证:AD\parallel OE.
2.(40')
一个矩形网格,水平边的长度为 a,竖直边的长度宽为 b,某人欲从左下角走至右上角。若 a=kb(k\in\mathbb{Z^+}),求证:第一步向右走的最短路径条数是第一步向上走的最短路径条数的 k 倍。
试问,满足 $\sigma(n)\times \varphi(n)$ 是完全平方数的正整数 $n$ 的个数是有限还是无限的?并证明你的结论。
其中,$\sigma(n)$ 表示 $n$ 的所有正约数和;$\varphi(n)$ 表示欧拉函数。
**注:作者于 2021/3/22 发现本题解答出锅,故临时替换。**
$3.(50')
设正整数列 \{a_n\}_{n\ge 3} 满足:对所有使得 2\le k\le n-1 的正整数 k,均有
a_{k+1}=\frac{a_k^2+1}{a_{k-1}+1}-1
试求 n 的所有可能值。
4.(50')
(2017 东南)设正实数 a_1,a_2,\cdots,a_{n+1},证明:
\sum\limits_{i=1}^na_i\times \sum\limits_{i=1}^na_{i+1}\ge \sum\limits_{i=1}^n\frac{a_ia_{i+1}}{a_i+a_{i+1}}\times \sum\limits_{i=1}^n(a_i+a_{i+1}).
二试模拟Ⅱ
我的评价:题目难度较契合近年真题难度。几何、代数难度可能略高于近年真题。
1.(40')
如图,\odot O_1 与 \odot O_2 交于 A,B 两点,C 为 \odot O_1 上任意一点。CA,CB 分别交 \odot O_2 于 E,D 两点,DE 交 \odot O_1,\odot O_2 于 X,Y。作 X 关于 AC 的对称点 X',作 Y 关于 CB 的对称点 Y'。证明:X'Y'\parallel AB。
2.(40')
设正实数 a_1,a_2,\cdots,a_n 满足 \sum\limits_{i=1}^n a_i=1。
证明:
1\le \sum\limits_{i=1}^n\frac{a_i}{\sqrt{1+\sum\limits_{j=1}^ia_j}\times\sqrt{\sum\limits_{j=i+1}^na_j}}<\frac \pi 2.
证明:
$$C_{ap}^{bp}\equiv C_a^b\pmod {p^3}.$$
$4.(50')$ 设 A 为一个 $3\times9$ 的小方格表。在 A 中每个小方格内各填一个正整数。若一个 $m\times n(1\le m\le 3,1\le n\le 9)$ 的方格表中所有数之和**不是** $10$ 的倍数,则称这个方格表是“好矩形”。对于 A 中的一个 $1\times1$ 的小方格,若它不被任何“好矩形”包含,则称这个小方格为“坏格”。求“坏格”个数的最大值。
------------
### 二试模拟Ⅲ
我的评价:由于东南、西部奥林匹克临近,此套模拟题难度高于联赛难度,请慎用!!
$1.(40')$ 设正实数 $a,b,c,x,y,z$ 满足 $xy+yz+zx=3$。证明:
$$\frac{a}{b+c}(y+z)+\frac{b}{c+a}(x+z)+\frac{c}{a+b}(x+y)\ge 3.$$
------------
$2.(40')$ 将边长为 $n$ 的正六边形分割成 $6n^2$ 个单位正三角形,并将这些正三角形黑白染色,使有公共边的两个三角形不同色。现在将 $2n$ 个硬币放入这些正三角形中,满足没有一个三角形中有两枚硬币,且没有两枚硬币在任何方向的同一“层”中(一个“层”指网格线中两条相邻的平行线之间的区域)。证明:恰有 $n$ 个硬币位于黑色三角形中。
------------
$3.(50')$ 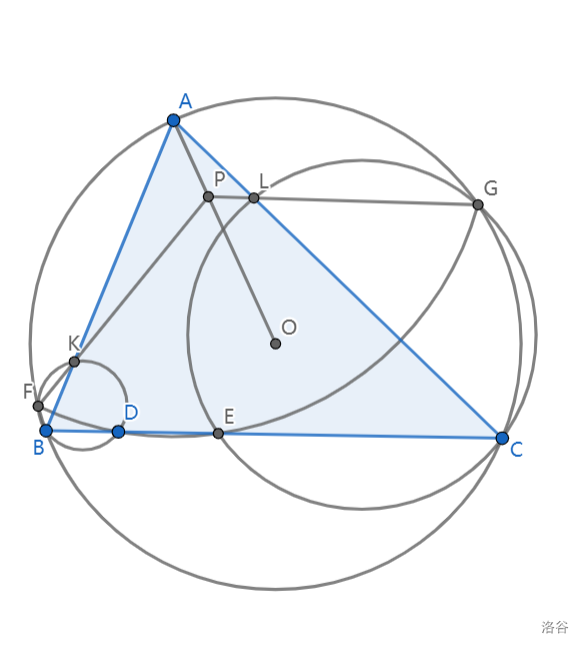
如图,$\triangle ABC$ 的外接圆为 $\odot O$。以 $A$ 为圆心作一圆,交 $BC$ 于 $D,E$,交 $\odot O$ 于 $F,G$。$\triangle BFK$ 的外接圆交 $AB$ 于 $K$,$\triangle CEG$ 的外接圆交 $AC$ 于 $L$。证明:$FK,GL,AO$ 三线共点。
------------
$4.(50')$ 将正整数集划分为 $n$ 个不交的无穷等差数列 $S_1,\cdots,S_n$,且它们的公差分别为 $d_1,\cdots,d_n$。证明:恰存在一个下标 $1\le i\le n$,使得
$$\frac{1}{d_i}\prod\limits_{j=1}^nd_j\in S_i.$$