讲稿-组合数学选讲

· · 个人记录

marp : true

headingDivider: 5

组合计数选讲

\texttt{by djwj233}

概念与约定

下面记：

由于时间问题，这里将仅给出证明的大致思路或正解的一个草图，繁琐的细节将被我们忽略.

本节课重点关注双射法在组合计数中的应用。

<!-- 双射法的本质是构造组合对象并从不同角度看该对象，借此证明组合恒等式.

双射法有狭义与广义之分，前者必须构造一一对应，后者则允许“多对一”“一对多”.

--- -->

<!-- 区别于代数方法，解决双射问题很像看图作文，大部分情况下你都需要对着式子天马行空地编出一个童话故事把它圆回去. 这个过程甚至往往不需要草稿纸.

可以说，在接受现代数学语言后，双射问题的硬性前置知识是没有的.

看上去双射问题很难有什么体系，但是在人们研究双射问题的过程中，人们还是总结归纳出了一些理论体系.

--- -->

以下内容大致分为四个部分：

要求

<!-- 你应当尽可能对下述问题给出尽可能优雅的只允许使用组合意义的解答.

这意味着下列解答将可能不会被我们接受：

不过在一些复杂问题中我们可能会允许使用出现后面几种情况以简化解答. -->

<!-- 我们的核心是降低解答难度，所以无论如何你都应保证：

你应当尽可能对下述问题给出优雅的组合意义证明。

由于课程的时间限制，给大家的思考时间较少. 如果各位可以在规定时间内独立完成所有题目，建议你踊跃投身前沿组合数学研究.

若无特殊说明，以下的所有变量都是 \mathbb N 中的元素. 题目难度不依次排列.

初等双射

P0

教程关：(2 min)

对于正整数 n，我们称一个正整数列 a_{1\cdots k} 是 n 的有序划分，当且仅当 \sum a_i=n。

给定 n(\ge 2)，求满足 \sum_{i=1}^k [2\mid a_i] 是偶数的有序划分个数。

答案是 2^{n-2}。

显然，n 的所有有序划分数量是 2^{n-1}，我们需要证明这里面一半为奇一半为偶。

对于一个有序划分，假如 a_1=1，那么我们把 a_1 和 a_2 合并得到一个新划分；反之若 a_1>1，我们把它拆成 1,(a_1-1) 两个数得到一个新划分。

容易发现，上述操作一定会改变 \sum_{i=1}^k [2\mid a_i] 的奇偶性。且这个映射是一个对合(involution，另译"内卷")，即有 f=f^{-1}。换言之，我们构造了一个从奇到偶的双射，这也就证明了两边的数量相等。

这是一大类双射问题的通用做法：构造一个不会映射到自己的对合，这样就可以把所有组合对象分为数量相等的两类。

我们再来看另一类双射。

P1

求解：(3 min)

\sum_{k=0}^m\binom{m+k}{k}2^{-k}

我们证明上式等于 2^m.

即证 \sum_{k=0}^m\binom{m+k}{m}2^{m-k}=2^{2m}，显然右边的意义是长为 2m 的 01 序列有多少种，我们证明它和左边相等.

对于一个长为 2m 的 01 序列，假如 0 在其中恰好有 m 个，那么这样的序列共有 \binom{2m}{m} 个.

否则我们在 \{0,1\} 中找到出现次数较多的数（众数），显然其出现次数至少为 m+1.

我们枚举其第 m+1 次出现位置为 m+k+1，其中 k\in [0,m-1].

这样 1\sim m+k 中的方案数就是 \binom{m+k}{m}，m+k+1\sim 2m 中的方案数是 2^{m-k}（m+k+1 位置上的数确定了众数），相乘再相加就是原式.

这类双射问题的特点是给等号两边找到一个相同的组合意义，也就是给等号左边的每个元素构造一个等号右边的元素，以证明二者数量相等。这个构造不一定是一个映射，它允许“多对一”“一对多”。

P2

求解：(5 min)

\sum_{k=0}^n\binom{2k}{k}\binom{2(n-k)}{n-k}

注意其代数解答是平凡的，因为 \sum_{k\ge 0}\binom{2k}{k}x^k=(1-4x)^{-0.5}，故上式应当等于 4^n. 下面给出一个组合证明：

右式的意义是从原点出发向右或向上走 2n 步，考虑解释左式.

我们设路径中最后一次触碰直线 y=x 是在 (k,k) 的位置，那么 (0,0)\to (k,k) 的方案数是 \binom{2k}{k}.

从 (k,k) 出发还可以走 2(n-k) 步，可以直接验证 k=n 时等式符合，下设 k<n，记 m=n-k.

若下一步向右走，那么其走到斜对角线 x+y=2n 而不触碰 y=x 的方案可以用类似于 Catalan 数的方法计算. 方案数是：

\sum_{0\le i<m} \binom{2m-1}{i}-\binom{2m-1}{i-1}=\binom{2m-1}{m-1}

把它乘以 2 就是 \binom{2m}{m}，这便是答案.

P3

求解：(7 min)

\sum_{i\ge 0}\binom{x+y+i}{i}\binom{y}{a-i}\binom{x}{b-i}

结论是：

\sum_{i\ge 0}\binom{x+y+i}{i}\binom{y}{a-i}\binom{x}{b-i}=\binom{x+a}{b}\binom{y+b}{a}

下面给出一个证明：

以下我们认为 b\le x+a\land a\le y+b，不难验证其余情况是平凡的.

考虑在两边同乘以 \dbinom{x+y}{x}，即证：

\sum_{i\ge 0}\binom{x+y+i}{x,y,i}\binom{y}{a-i}\binom{x}{b-i}=\binom{x+y}{x}\binom{x+a}{b}\binom{y+b}{a}

考虑如下实际问题：

我们有足够多个有标号物品，现在要从这些有标号物品中选择若干个物品组成集合 X,Y,A,B，需要满足：

这样，我们枚举 i=|A\cap B| 后，左式的组合意义显然. 我们解释右式.

若 T\subseteq S，且我们对 i\in [1,|T|] 确定了 T 中第 i 大的元素在 S 中是第几大，则称我们掌握了信息 (T,S).

容易看出右式相当于枚举了 (X,X\cup Y),(B,X\cup A),(A,Y\cup B) 这三个信息，只需证明从任意这三个信息出发可以确立一组全序即可.

我们只需要从小到大依次确定每个元素在哪里即可，现在我们把问题转化为寻找最小元素在哪里.

利用 (X,X\cup Y) 中信息，不妨设 \min X<\min Y，讨论：

P4

求证：（x\in \mathbb R）(4 min)

\sum_{k=0}^n \binom{n}{k}^2x^k=\sum_{k=0}^n\binom{2n-k}{n-k,n-k,k}(x-1)^k

我们以下认为 x\in \mathbb N_+.

注意到右式其实是 \displaystyle \sum_{k=0}^n\dbinom{n}{k}\binom{2n-k}{n}(x-1)^k，那么组合意义就显然了：

只需建立二者间的双射，这是简单的：

停停，这里不是只对 x\in \mathbb N_+ 证明了上述结论吗？

事实上，由于等式的两边都是次数有限的多项式，而我们对于无穷多个 x 都证明了两边相等. 从而依线性代数的有关结论，可以证明两边多项式的各项系数均相等，从而对任意实数上式均成立.

这种推理方式被我们称为多项式推理法.

P5

称正整数数列 a 是合法的当且仅当它是 n 的有序划分，分别求出：（6 min）

\sum_{a \text{ is valid}} \prod_{j=1}^k a_j

和

\sum_{a \text{ is valid}} \prod_{j=1}^k (2^{a_j-1}-1)

答案分别是 F_{2n-1},F_{2n-3}，其中 F 是斐波那契数列。

使用代数做法可以得到答案，但是没法直观地看出这是斐波那契数列。

前者是不难的，考虑画出 n 个圆圈，每两个圆圈间画一个点，共 2n-1 个元素。不难发现，选择这 2n-1 个元素的一个子集，使得：

这样的方案数就是 \sum_{a \text{ is valid}} \prod_{j=1}^k a_j。

而我们考虑把 2n-1 划分成若干个 1,2 之和以后，选择所有大小为一的块所包含的元素。可以证明这和上面的条件等价。证毕。

对于第二个问题，我们先考虑一下怎么给 2^{a_i-1}-1 找到与“划分为 1/2”有关的组合意义。

对于一个 a_i，我们把 2a_i 划分为若干段，每段长为 1 或 2，满足：

比如，a_i=3 时所有的划分方案为：

11112 1212 1122

容易证明方案数为 2^{a_i-1}-1。（在最后一个 1 之后人为补上一个 1 分析）

直接把 a_{1\cdots k} 中 k 段这样的东拼到一起，总长是 2n。但是由于开头的 1 和末尾的 2 是固定的，可能的方案数只有 F_{2n-3} 种。

现在只需要证明每种方案只有一种可能的划分方式。这是容易的：从前往后找到第一个 2 满足其前面的 1 的个数是偶数，显然第一段只能是在它后面划分；以此类推不断划分下去即可。

证毕。

<!-- ### EXTRA

前沿数学.

证明

\large \dfrac{\binom{2m}{m}\binom{2n}{n}}{2\binom{n+m}{n}}

总是整数. （这被称为 super Catalan numbers. ）

有一个显然的代数方法是分析每个质因子的出现次数，但是它没法给出上式的组合意义.

在 2014 年有人利用 2-Motzkin Paths 给出了一个组合证明. 有兴趣的同学可以自行阅读. -->

排列、置换与划分

注意以下内容的概念和记号很可能不通用，很多名词都是我自己的翻译 / 命名结果.

限于篇幅和时间问题，这里将不会展开具体应用，性质大都也是点到为止.

置换的循环结构

记 \mathfrak{S}_n 为 [n] 上的置换/排列构成的集合.

我们知道，任意一个置换 p 都可以被唯一地拆成若干循环的复合，使得每个 [n] 中的元素恰好在一个循环中，如 [4,2,1,3] 就可以被表示为 (2)(4\ 3\ 1) 的形式. 这个过程被我们称为循环分解.

若我们对所有 i\to p_i 连边，在直观上构成了若干个环，这也是 OI 中常用的置换环结构.

定义置换 w 的标准表示 \widehat{w} 为：

如 [4,2,7,1,3,6,5] 会变成 (2)/(4,1)/(6)/(7,5,3)，也就是 [2,4,1,6,7,5,3].

可以证明 \mathfrak{S}_n\ \hat{\to}\ \mathfrak{S}_n 构成了双射（证明留作习题），因此这也被我们称为基础双射 (fundamental bijection).

P0

记 c_i 表示 w 中长度为 i 的循环个数，称 c_{1\cdots n} 为 w 的类型. 今证明

设上述置换构成的集合为 \mathfrak{S}^c_n. 有：

证毕.

此公式给出了一个简单的代数结论，因此非常强大，可以帮助我们使用初等代数方法解决很多与循环拆分有关的问题.

借助于多元生成函数，此结论还可以发挥更大的作用，但这里不再展开.

P1

来做个简单的习题：

考虑在基础双射中，n 在 w 中大小为 k 的循环内当且仅当其在 \widehat{w} 中排在第 n-k+1 位，故可以得到答案就是 \frac{1}{n}，与 k 无关，非常神奇.

P2

可以得到答案是 \frac{1}{k}\sum_{i=1}^n [i\ \text{所在的循环大小为}\ k]=\frac{1}{k}.

排列的统计学性质

为了方便，以下我们认为对于任意 n 阶正整数序列 w_{1\cdots n}，只要 \forall i\ne j,w_i\ne w_j，w 就可以被用来表示一个排列 / 置换. 其值等于将 w 离散化到 [n] 中后的数列，如 [1,4,3] 等价于排列 (1,3,2).

P0

定义一个排列 p 的逆序对 \text{inv}(p)=\sum_{1\le i<j\le n}[p_i>p_j]，今证明

注意到一对在 \text{inv}(p) 中有贡献的 i,j，其在 \text{inv}(p^{-1}) 中仍然有贡献，且这个条件是充要的，立刻得到原结论. 证毕.

P1

定义 p 的下降集合 (descent set) \text{D}(p)=\{i\in [n-1]\mid p_i>p_{i+1}\}，其主指标 (major index) \text{maj}(p)=\sum_{i\in \text{D}(p)}i. 今证明

我们递归地构造双射 \varphi:\mathfrak{S}_n\to \mathfrak{S}_n. （注意这个 \varphi 的定义非常重要，我们之后还会用到）

需要注意的是，此处的证明并不是直接双射的（使用了归纳），事实上对此的直接双射证明仍是 open problem.

--- 对 $w\in \mathfrak{S}_n$，我们令 $v=\varphi'(w_{1\cdots n-1})$（这里的 $w_{1\cdots n-1}$ 表示把这些数取出离散化后的 $n-1$ 阶置换）. 把 $v$ 看作一个长为 $n-1$ 的序列，然后做一些调整： - 若 $w_n>w_{n-1}$，我们在每个满足 $w_i<w_n$ 的 $i$ 之后切一刀，把 $v$ 分为若干部分；对于每个部分，将其向右循环移一位. - 否则 $w_n<w_{n-1}$，我们在每个满足 $w_i>w_n$ 的 $i$ 之后切一刀，同样把每部分向右循环移一位. 这样我们得到一个新的序列 $v'$，现在我们令 $\varphi(w)_i=v'_i(1\le i<n)$ 且 $\varphi(w)_n=w_n$，这便完成了 $\varphi(w)$ 的构造. --- 易证 $\varphi$ 是双射. （证明只需构造 $\varphi^{-1}$ 即可）接下来我们只需要证明 $\text{maj}(w)=\text{inv}(\varphi(w))$. 依然考虑归纳，记 $p=w_{1\cdots n-1}$. - 若 $w_{n-1}<w_n$，则 $\text{maj}(w)=\text{maj}(p)$，对比一下上面的调整过程可以发现 $\text{inv}(\varphi(w))=\text{inv}(v)$ 成立. - 否则 $\text{maj}(w)=\text{maj}(p)+n-1$，依然可以证明此时 $\text{inv}(\varphi(w))=\text{inv}(v)+n-1$ 成立. 证毕. 由上，$\varphi$ 也可被视作 $\{p\in \mathfrak{S}_n\mid \text{inv}(p)=k\}\to \{p\in \mathfrak{S}_n\mid \text{maj}(p)=k\}$ 的双射. #### P2 记 $\text{ID}(w)=\text{D}(w^{-1})$，今证明 - 上述 $\varphi$ 是**保 $\text{ID}$ 的** ($\varphi$ preserves $\text{ID}$)，即 $\text{ID}(w)=\text{ID}(\varphi(w))$; --- 若其出错，即存在一个 $i$ 使得 $i+1$ 在 $w$ 中在 $i$ 前面而 $i+1$ 在 $\varphi(w)$ 中在 $i$ 后面（或其对称情况）. 归纳地，条件等价于"在上面的调整过程中二者间的位置关系改变了"，那么显然 $i$ 和 $i+1$ 不能是 $w_n$. 我们注意到若 $i$ 和 $i+1$ 不在同一个部分中，二者间的位置关系不会改变，现在只剩下二者在同一个部分中的情况. 容易证明二者中不可能有一个是某个部分的段尾，这样显然二者间的位置关系也不会改变. 证毕. #### P3 记 $\text{imaj}(w)=\text{maj}(w^{-1})$，今证明 - $\text{inv},\text{maj},\text{imaj}$ 是**两两交对称分布** (symmetric joint distribution)的. 即： $$ \forall x,y\in \mathbb N, \begin{cases} \#\{p\in \mathfrak{S}_n\mid \text{inv}(p)=x,\text{maj}(p)=y\}= \#\{p\in \mathfrak{S}_n\mid \text{inv}(p)=y,\text{maj}(p)=x\}\\ \#\{p\in \mathfrak{S}_n\mid \text{inv}(p)=x,\text{imaj}(p)=y\}= \#\{p\in \mathfrak{S}_n\mid \text{inv}(p)=y,\text{imaj}(p)=x\}\\ \#\{p\in \mathfrak{S}_n\mid \text{maj}(p)=x,\text{imaj}(p)=y\}= \#\{p\in \mathfrak{S}_n\mid \text{maj}(p)=y,\text{imaj}(p)=x\} \end{cases} $$ --- 第三条是显然的：只需考虑映射 $w\to w^{-1}$. 此外我们注意到 $\varphi$ 是保 $\text{ID}$ 的，那么自然也保 $\text{imaj}$，这样第二条是自然的：因为它可以直接和第三条中的等号接上. 由 $\text{inv}(p)=\text{inv}(p^{-1})$ 立刻得到第一条. 证毕. #### P4 记 $\text{des}(p)=\#\text{D}(p)$，回顾一下定义：$\text{des}$ 的分布被我们称为**欧拉数** $\left\langle \begin{matrix} n \\ m\end{matrix}\right\rangle$，其满足： $$ \left\langle \begin{matrix} n \\ m\end{matrix}\right\rangle=(n-m)\left\langle \begin{matrix} n-1 \\ m-1\end{matrix}\right\rangle+(m+1)\left\langle \begin{matrix} n-1 \\ m\end{matrix}\right\rangle $$ 边界条件是 $\left\langle \begin{matrix} n \\ m\end{matrix}\right\rangle=0(m\ge n),\left\langle \begin{matrix} n \\ 0\end{matrix}\right\rangle=1(n\ge 0)$. --- 定义 $i$ 是 $p$ 的**超限位置** (excedance, 这其实是 exceedance 的错拼, 但已广为使用)，当且仅当 $p_i>i$. 同理若 $p_i\ge i$ 则称其为**弱超限位置** (weak excedance). 记 $\text{exc}(p)$ 为 $p$ 的超限位置数量，$\text{wexc}$ 为弱超限位置数量. 今证明 - $\text{exc}$ 和 $\text{des}$ 等分布. - $\text{wexc}-1$ 和 $\text{des}$ 等分布. --- 先证后者. 考虑排列 $w$ 在基础双射下的像 $\widehat{w}$，易证 $$ \begin{aligned} \forall 1\le i<n, \widehat{w}(i)<\widehat{w}(i+1)&\Leftrightarrow ((w(\widehat{w}(i))\ne \widehat{w}(i+1))\lor (w(\widehat{w}(i))=\widehat{w}(i+1) \land \widehat{w}(i)<\widehat{w}(i+1)))\\ &\Leftrightarrow {\color{red}\widehat{w}(i)\le w(\widehat{w}(i))} \end{aligned} $$ 注意必须这里是 $\le$ 而不是 $<$. 另一方面我们有 $\forall 1\le i\le n, \widehat{w}(i)\le w(\widehat{w}(i))\Leftrightarrow (\widehat{w}(i)<\widehat{w}(i+1)\lor i=n)$，故 $n-\text{des}(\widehat{w})=\text{wexc}(w)$. 这给出 $$ \#\{w\in \mathfrak{S}_n\mid \text{wexc}(w)=k\}=\#\{w\in \mathfrak{S}_n\mid \text{des}(w)=n-k\}=\#\{w\in \mathfrak{S}_n\mid \text{des}(w)=k+1\} $$ 后一个等号只需考虑把排列反向后，其 $\text{des}'=(n-1)-\text{des}$. --- 对于前者只需考虑取双射 $f$： $$ f(w)_i= \begin{cases} 1 & \text{if }w_i=n\\ w_i+1 & \text{otherwise} \end{cases} $$ 这样 $f(w)_i>i\Leftrightarrow w_i\ne n\land w_i\ge i$，而 $w_i=n\Rightarrow w_i\ge i$，故 $\text{exc}(f(w))=\text{wexc}(w)-1$。 证毕. --- 综上所述，我们使用上面几条引理刻画了排列的一些统计学性质. 陈列如下： - 排列的逆保 $\text{inv}$. - $\text{maj}$ 和 $\text{inv}$ 等分布. （证明时引入了双射 $\varphi$.） - $\varphi$ 保 $\text{ID}$ 和 $\text{imaj}$. - $\text{inv},\text{maj},\text{imaj}$ 两两交对称分布. - $\text{exc}$ 和 $\text{des}$ 等分布. - $\text{wexc}-1$ 和 $\text{des}$ 等分布. ### 下降集合与 w-兼容性 以下我们设 $w$ 为任意 $n$ 阶置换（即 $w\in \mathfrak S_n$）. #### P1 我们称 $f:[n]\to \mathbb N$ 是 **$w$ - 兼容** ($w$ - compatible) 的，记为 $f\vdash w$，当且仅当： - $f(w_1)\ge f(w_2)\ge \cdots\ge f(w_n)$; - $i\in \text{D}(w)\Rightarrow f(w_i)>f(w_{i+1})$. 今证明：任意 $f:[n]\to \mathbb N$ 总是与且仅与某个 $w$ 兼容. ----- 按照值把 $f(i)$ 分为数段，容易发现对于一个极大的形如 $f(i_1)=f(i_2)=\cdots = f(i_L)$ 的段， 一定可以确定出 $l,r$ 使得 $w_j\in I\Leftrightarrow l\le j\le r$，其中 $I=\{i_1,i_2,\cdots,i_L\}$. 我们只需要分配 $w_{l\cdots r}$ 的值. 不妨设 $i_1<i_2<\cdots<i_L$，在段内我们需要保证 $w_i$ 单调递增，那么就是 $w_l=i_1,w_{l+1}=i_2,\cdots$，这个构造是唯一的. 证毕. #### P2 定义 $\mathcal A(w)=\{f:[n]\to \mathbb N\mid f\vdash w\},\mathcal A_m(w)=\{f:[n]\to [m]\mid f\vdash w\}$. 今证明 $$ \# \mathcal A_m(w)=\binom{m+n-1-\text{des}(w)}{n} $$ --- 考虑对于 $f\in\mathcal A_m(w)$ 构造 $f'$： - 先令 $f'=f$; - 依次地对于每个 $w_i>w_{i+1}$ 的位置，把 $f'(w_{1\cdots i})$ 这些位置的值都减去 $1$. 容易发现 $f$ 和 $f'$ 是双射，而 $f'$ 满足 $$ m-\text{des}(w)\ge f'(w_1)\ge f'(w_2)\ge \cdots\ge f'(w_n)\ge 1 $$ 使用插板法即可证明上述结论. 证毕. #### P3 今给出 $$ \sum_{f\in \mathcal A(w)} x^{\sum_{i=1}^n f(i)}=\dfrac{x^{\text{maj}(w)}}{\prod_{i=1}^n(1-x^i)} $$ --- 先类似地建立 $f$ 到 $f'(w_1)\ge f'(w_2)\ge \cdots\ge f'(w_n)\ge 0$ 的双射（注意此处 $f$ 是无界的），那么显然有 $$ \sum_{i=1}^n f(i)=\text{maj}(w)+\sum_{i=1}^n f'(i) $$ 这消去了右式的分子. --- 对于分母，代数地理解它是不难的，上式也即：（下面认为 $f(0)=0$） $$ \begin{aligned} &\sum_{f'} x^{\sum_{i=1}^n f'(i)}\\ =&\sum_{f'} \prod_{i=1}^n x^{(f'(i)-f'(i-1))(n-i+1)}\\ =&(1+x+x^2+\cdots)(1+x^2+x^4+\cdots)\cdots(1+x^n+x^{2n}+\cdots)\\ =&\dfrac{1}{\prod_{i=1}^n(1-x^i)} \end{aligned} $$ 其中第三行的第 $i$ 个括号相当于在枚举 $f(n-i+1)-f(n-i)$ 的值. 证毕. --- 让我们再关注一下分母部分的证明. 设形如 $f'(w_1)\ge f'(w_2)\ge \cdots\ge f'(w_m)\ge 0(m\le n)$ 的 $f'$ 构成的集合为 $\mathcal A_{(m)}(w)$， 那么我们本质上对 $1\le m\le n$ 建立了一个 $\mathcal A_{(m)}(w) \to \mathcal A_{(m)}(w)\cup \mathcal A_{(m-1)}(w)$ 的双射： - 对 $f'\in \mathcal A_{(m)}(w)$，若 $f'(w_m)=0$，直接删去之可对应至 $\mathcal A_{(m-1)}(w)$ 的一员；否则将 $f'$ **整体**减去 $1$，对应至 $\mathcal A_{(m-1)}(w)$ 的一员. 从这方面也可以解释上面的生成函数： > 分母中的 $\dfrac{1}{1-x^m}$ 相当于在枚举我们在 $\mathcal A_{(m)}(w)$ 通过上述双射到达 $\mathcal A_{(m-1)}(w)$ 的"进程"中执行了几次整体减一. 我们已经使用上面三条结论刻画了兼容的形态，考虑应用之解决一些实际问题. #### P4 证明 $$ \forall k\in \mathbb N, \left(\sum_{n\ge 0} n^kx^n\right)(1-x)^{k+1}=\sum_{i=1}^k \left\langle \begin{matrix} k \\ i-1\end{matrix}\right\rangle x^i $$ --- 只需证 $$ n^k=\sum_{i=1}^k\left\langle \begin{matrix} k \\ i-1\end{matrix}\right\rangle\binom{k+n-i}{n-i} $$ 注意到 $n^k=\#\{f:[k]\to[n]\}$，故 $$ n^k=\sum_{w\in \mathfrak S_k}\# \mathcal A_n(w)=\sum_{w\in \mathfrak S_k}\binom{n+k-1-\text{des}(w)}{k}=\sum_{w\in \mathfrak S_k}\binom{n+k-(\text{des}(w)+1)}{n-(\text{des}(w)+1)}=\sum_{i=1}^{k}\left\langle \begin{matrix} k \\ i-1\end{matrix}\right\rangle\binom{k+n-i}{n-i} $$ 这便是上式了. 证毕. --- **在实际问题中出现时，$\left\langle \begin{matrix} k \\ i-1\end{matrix}\right\rangle$ 往往以 $\#\{w\in \mathfrak{S}_k\mid \text{wexc}(w)=i\}$ 等更为隐蔽的形式出现**，因此务必牢记上面一节"排列的统计学性质"中讲过的性质，不要被遮蔽了双眼. ### 划分与五边形数 我们记 $\lambda=(\lambda_1,\lambda_2,\cdots,\lambda_{l})$ 是 $n$ 的划分，记为 $\lambda\vdash n$，当且仅当 $\lambda\in \mathbb N^l,\sum \lambda_i=n$ 且 $\lambda_i\ge \lambda_{i+1}$. 由定义，显然所有的划分与满足 $p\in \mathbb N^n,\sum ip_i=n$ 的 $p$ 双射. 若无特殊说明，以下有 $\lambda\vdash n$. #### P0 证明：对于任意正整数 $n\ge 2$，把 $n$ 划分为若干 $2$ 的次幂的方案数总是偶数. --- 简单题. 考虑对于一种划分方案，设划分中出现的最大的数是 $2^k$. 若其只出现一次则将其删去变成两个 $2^{k-1}$，否则将两个 $2^k$ 变为 $2^{k+1}$. 容易发现我们构造的映射是一个对合。此外，这个映射不会有射到自己的情况. 证毕. > 注意到该映射一定会改变划分中 $l$ 的奇偶性，因此也有一些其它用途. #### P1 一个有趣的小结论. 设 $f_{\lambda}(k)=\sum_i [\lambda_i=k],g_{\lambda}(k)=\sum_{i=1}^n [k\le \sum_j [\lambda_j=i]]$，今给出： $$ \forall k, \sum_{\lambda\vdash n}f_{\lambda}(k)=\sum_{\lambda\vdash n}g_{\lambda}(k) $$ 但是注意对于一个 $k$，$f_{\lambda}(k),g_{\lambda}(k)$ 不一定是等分布的. --- 考虑对 $\{(\lambda,i)\mid 1\le i\le f_{\lambda}(k)\}$ 和 $\{(\lambda,i)\mid 1\le i\le g_{\lambda}(k)\}$ 找到一个双射. 对前者中的 $(\lambda,i)$，我们在 $\lambda$ 中删去 $i$ 个 $k$，加入 $k$ 个 $i$ 得到 $\lambda’$，一定有 $k\le \sum_j [\lambda'_j=i]$，故只需令 $i'$ 为 $\sum_{t=1}^i[k\le \sum_j [\lambda'_j=t]]$. 这样我们得到了 $(\lambda',i')$，易见这是双射. 证毕. #### P2 证明： $$ \sum_{\lambda\vdash n}f_{\lambda}(2)=\sum_{\lambda\vdash \color{red}n-1}\sum_{i=1}^{n-1} [1= \sum_j [\lambda_j=i]] $$ --- 即证 $\sum_{\lambda\vdash n}f_{\lambda}(2)=\sum_{\lambda\vdash n-1}(f_{\lambda}(1)-f_{\lambda}(2))$. 同样地我们考虑对 $(\lambda, i),1\le i\le f_{\lambda}(1)$ 找到组合意义. 设 $f_{\lambda}(1)=k$，若 $i\le \frac{k}{2}$ 则把 $2i$ 个 $1$ 换为 $i$ 个 $2$，对应到 $(\lambda'\vdash n-1,i)$ 上；否则先加入一个 $1$ 再把 $2(i-\left\lfloor\frac{k}{2}\right\rfloor)$ 个 $1$ 换为 $i-\left\lfloor\frac{k}{2}\right\rfloor$ 个 $2$，对应到 $(\lambda'\vdash n,i-\left\lfloor\frac{k}{2}\right\rfloor)$ 上. 容易发现这是双射. 证毕. #### P3 我们定义**广义五边形数** (generalized pentagonal numbers) $n$ 为所有形如 $\dfrac{3k^2\pm k}{2}$ 形式的数，其中 $k\in \mathbb N$. 需要证明： $$ [x^n]\prod_{i=1}^{\infty}(1-x^i)=\begin{cases}(-1)^k & , \text{if } n=(3k^2\pm k)/2\\ 0 & ,\text{otherwise} \end{cases} $$ --- 展开后，其意义为： > 对于所有 $n$ 的元素互不相同的划分，记其权值为 $(-1)^l$，其中 $l$ 为其长度。原式即为所有 $n$ 的划分的权值和。 --- 我们希望建立一个从奇数长度划分到偶数长度划分的“几乎双射”。以下给出： > 我们记 $t(\lambda)$ 为一个最大的 $p$ 使得 $\forall i\le p,\lambda_i=\lambda_1-i+1$。 > > - 若 $t(\lambda)\ge \lambda_l$，则移除 $\lambda_l$ 并让 $\lambda_1\sim\lambda_{\lambda_l}$ 每个都加一； > - 若 $t(\lambda)< \lambda_l$，则让 $\lambda_1\sim\lambda_{t(\lambda)}$ 每个都减一，加入一个 $\lambda_{l+1}=t(\lambda)$。 > > 显然该映射总是把 $l$ 的奇偶性反转，而且它还是一个对合。唯一的问题是在一些情况下这个映射可能不合法，上述性质也就无从谈起。经过细致的讨论，我们发现只有当 $t(\lambda)=l$ 且 $\lambda_l-1\le t(\lambda)\le \lambda_{l}$ 时该映射直接不合法。可以证明，把这些情况粗暴地排除后，上述映射就是一个完美的对合了。 这样我们只需要分析 $t(\lambda)=l$ 且 $\lambda_l-1\le t(\lambda)\le \lambda_{l}$ 这个 corner case 带来的影响，简单计算可以发现这就是上面的 $(-1)^k$ 了。 证毕. #### P4 证明：（$n>0$） $$ [x^n]\sum_{i=1}^{\infty}(-x)^i\prod_{j=1}^{i-1}(1+x^j)=\begin{cases}-1 & , \text{if } n=(3k^2- k)/2\\1 & , \text{if } n=(3k^2+ k)/2 \\ 0 & ,\text{otherwise} \end{cases} $$ 只需注意到上述“几乎双射”同样反转了 $\lambda_1$ 的奇偶性即证。 #### P5 $$ [x^n]\sum_{i=1}^{\infty}x^{2i-1}\prod_{j=2i}^{\infty}(1-(-x)^j)=\begin{cases}1 & , \text{if } n=k^2\\ 0 & ,\text{otherwise} \end{cases} $$ --- 我们故技重施，依旧考虑构造一个“几乎双射”，满足： - 它交换偶元素个数的奇偶性； - 在且仅在 $(1,3,5,7,9,\cdots,2k-1)$ 处失效。 - 它最好还是一个对合。 第二点是一个非常强的条件！我们已经大致可以预想，这个映射对于划分中只有奇数的情况应当表现为“把排列中最大的一段连续奇数都减 $2$” 然后变成什么东西。完善一下细节，可以给出： > 我们把 $\lambda$ 中的所有奇数取出，从大到小排列为 $o_{1\cdots d}$，再记 $b$ 为一个最大的数使得 $\forall i\le b,o_i=o_1-2(i-1)$. > > 设 $\lambda$ 中最小的偶数为 $v$（若没有偶数则 $v=\infty$）： > > - 若 $2b<v$，我们便把 $o_{1\cdots b}$ 各自减去 $2$，再在 $\lambda$ 中加入一个 $2b$； > - 若 $2b\ge v$，我们把 $v$ 删掉，把 $o_{1\cdots b}$ 各自加上 $2$。 显然 $b\ge 1$，因此可以验证这是个对合。证毕。 ### 排列的笛卡尔树结构 这应当是联赛内容，不再赘述，来道例题吧. ---- （APIO2023 讲课题的一个加强版） 记一个长为 $n$ 的整数序列 $a_{1\cdots n}$ 为**好**的，当且仅当 $a$ 中每个数在 $[1,m]$ 之间，且 $[1,m]$ 间的每个整数都在 $a$ 中出现过. 在一个序列 $a$ 中，我们记 $a_x$ 比 $a_y$ 大，当且仅当 $a_x>a_y$ 或 $a_x=a_y,x<y$. 设 $f_a(l,r)$ 为 $a_{l\cdots r}$ 中最大值的下标，记两个序列 $a_{1\cdots n},b_{1\cdots n}$ 是**同态**的，当且仅当： - $\forall 1\le l\le r\le n, f_a(l,r)=f_b(l,r)$. 给定 $n,m$，求有多少种不同态的好数列，答案对 $998244353$ 取模. 多测，$1\le T\le 20,1\le n,m\le 10^6$. --- 随便给的部分分： - Subtask 1：5 分，$m=1$. - Subtask 2：5 分，$m>n$. - Subtask 3：5 分，$n\le 5$. - Subtask 4：15 分，$m=n$. - Subtask 5：5 分，$m=n-1$. - Subtask 6：10 分，$n\le 300$. - Subtask 7：1 分，$T=1,n\le 10^5$. - Subtask 8：19 分，$T\le 10,n\le 2000$. - Subtask 9：15 分，$m\ge \dfrac{n}{2}$. - Subtask 10：20 分，无特殊限制. 前三个部分应该是平凡的. ---- APIO2023 讲课中利用生成函数方法给出了一个单 log 做法，难免不尽如人意. 今给出 $\mathcal O(n+m)$ 做法. 这个题目需要多步双射，我们一步一步来. **第一步：笛卡尔树.** 显然，两个数列同态当且仅当其大根堆形式的笛卡尔树形态相同. <!-- > 一方面，对于两个同态序列 $a_{1\cdots n},b_{1\cdots n}$，由 $f_a(1,n)=f_b(1,n)$ 知其笛卡尔树的根的坐标肯定相同. > > 由于两个同态序列对应位置的子区间也同态，所以归纳可知两边子树形态相同. > > 另一方面，若两序列 $a_{1\cdots n},b_{1\cdots n}$ 笛卡尔树形态相同，则 $f_a(l,r)=\text{LCA}(l,r)$ 也相同. > > 证毕. --> 这样我们把问题转化为： > 计算树 $T$ 的数量，使得至少存在一种好的序列，其笛卡尔树为 $T$. 由于所有 $n$ 阶排列的笛卡尔树必然能取遍所有 $n$ 个结点的二叉树，所以 Subtask 4 能做了. Subtask 4：此问题即计算所有 $n$ 个点的二叉树的个数，即 $\text{Catalan}_n$. ---- **第二步：竖直左链、水平右链.** 根据题意，对笛卡尔树上每个结点，其左儿子的权值一定小于其本身，而右儿子的权值只需要不大于其本身. 这意味着，至少存在一种好的序列使其笛卡尔树为 $T$ 的一个必要条件是： > 对于树上的每个点，它到根的路径上是左儿子的点的数量（包括根）不超过 $m$. 否则 $1\cdots m$ 的数无法满足“左儿子的权值一定小于其本身”这一需求. ---- 我们通过构造证明，这个条件也是充分的. 大致的一个过程是：先按深度一层层染色，要是还有剩的，就按层数倒着染回来. 证毕. ---- 不难想到，对于一棵笛卡尔树，我们将其左儿子与父亲竖直画，右儿子与父亲水平画，那么问题转换为： > 计算笛卡尔树 $T$ 的数量，使得用竖直左链、水平右链的形式表示后，其树高（即代码中的 $dep$）不超过 $m$. 这样 Subtask 5 / 6 / 7 就能做了. Subtask 5： 树高不超过 $n-1$ 的笛卡尔树就是所有二叉树减去树高恰为 $n$ 的二叉树，后一部分只有一种可能：它是一条左偏链. 所以答案是 $\text{Catalan}_n-1$. ---- Subtask 6： 设 $dp_{n,m}$ 为树高 $\le m$，点数恰为 $n$ 的树的数量，则 $dp_{0,m}=1$，且： $$ dp_{n,m}=\sum_{x=1}^n dp_{x-1,m-1}dp_{n-x,m} $$ 这样就可以 $\mathcal O(n^2m+T)$ 了. Subtask 7：把这个东西写成生成函数形式可以得到 $F_m(x)=\dfrac{1}{1-xF_{m-1}(x)},F_0(x)=\dfrac{1}{1-x}$. 硬解可以解出一个通项式，可以 $O(Tn\log n)$ 做，过掉 Subtask 7. ----- **第三步：普通树.** 普通树和二叉树的双射有一种方法叫做左儿子右兄弟，我们试试. 对每个二叉树，我们建一棵普通树，满足： - 每个点在二叉树上的左儿子是其在普通树上的最左边的儿子； - 每个点在二叉树上的左儿子是其在普通树上的右兄弟. 判断重复的方法是每个点的儿子顺序一定，容易证明这是双射. 不过其实这东西建出来是一片森林，所以可能上面的表述有点不太严谨. ---- 问题转化为： > 求 $n$ 个点的（上面定义下的）有根树森林的数量，使得每棵树的树高不超过 $m$. **第四步：括号序列与 $\pm 1$ 序列.** 由于每个点的儿子顺序一定，不难想到转化为括号序列. 具体地，维护一个括号序列，在进入子树时添加一个左括号，在出子树时添加一个右括号. 把上面的 `(` 当作 $+1$，`)` 当作 $-1$，我们发现问题转化为： > 求 $\pm1$ 序列的数目，使得每个前缀和 $S_i$ 满足 $0\le S_i\le m$. Subtask 8：记 $dp_{i,j}$ 为长为 $i$ 且当前和为 $j$ 的 $\pm1$ 序列数量，可以 $\mathcal O(nm)$ DP，总复杂度 $\mathcal O(Tnm)$. ---- **第五步：折线.** 将 $\pm 1$ 序列画在一个 $n\times n$ 的网格图中，$+1$ 就是向上走，$-1$ 就是向右走. 这样问题转化为： > 求 $(0,0)$ 到 $(n,n)$ 的上述路径数，使得路径不碰到 $y=x-1$ 或 $y=x+m+1$. --- **第六步：翻折.** 容斥！ 实际上这里的容斥非常复杂，六步双射只是问题的刚刚开始. 我们先保证路径无论如何都不经过 $y=x-1$，这样答案数就是： > 不经过 $y=x-1$ 的方案数 减去 经过 $y=x+m+1$ 但是不经过 $y=x-1$ 的方案数. "不经过 $y=x-1$ 的方案数"就是卡塔兰数，它的推导过程叫做 [Gessel-Viennot Cancellation](http://people.brandeis.edu/~gessel/homepage/papers/pp.pdf)，大致思路是对不合法路径通过翻折构造双射. --- Subtask 9：注意到 $m\ge \dfrac{n}{2}$ 时经过 $y=x+m+1$ 对称的 $y=x-1$ 不可能被 $(-m-1,m+1)$ 碰到，所以可以直接一步容斥. ---- 正解需要更复杂的容斥，大致思路是递归下去. 设 $f(u,a,b,pre)$ 表示下列问题的答案： > 有一个 $u$ 行 $2n-u$ 列的格子，从左下走到右上，碰到 $y=x-b$ 是被禁止的. > > 另外，在第一次碰到 $y=x-pre$ 前碰到 $y=x+a$ 也是被禁止的. ------- 若 $x=0$ 则 $f(x,a,b,pre)$ 要么是 $0$ 要么是 $1$，直接返回. 若 $a>x$ 则就返回 $\dbinom{2n}{x}-\dbinom{2n}{x+b}$. 否则： $$ f(x,a,b,pre)=\dbinom{2n}{x}-\dbinom{2n}{x+b}-f(x-a,pre,2a+b,a) $$ 答案即 $f(n,m+1,1,1)$. 注意到递归时 $a>0$，故每次 $x$ 都是在减小的，复杂度 $\mathcal O(n)$. ## 树与 Prufer 序列 ### P0 设 $n\ge 2$ 为一个正整数. - 求 $n$ 个点的有标号无根树数量. - 求 $n$ 个点的有标号有根树数量. - 求 $n$ 个点的有标号有根森林数量. ---- 第一问就是 Prufer 序列的直接推论，答案为 $n^{n-2}$. > 回忆一下 Prufer 序列的构造过程： > > 1. 从树上选择编号最小的叶子结点并在序列末尾加入其父结点（其唯一连向的结点）的编号；删去该叶子. > 2. 重复操作直到树只剩下两个结点，此时序列的长度刚好为 $n-2$. > > 可以得到从 Prufer 序列到树的构造过程，因此构成双射. 容易发现，每个度数为 $d$ 的点恰好在序列中出现 $d-1$ 次. --- 易见第二问的答案为第一问答案乘 $n$，即 $n^{n-1}$； 第三问答案为 $n+1$ 个点的有标号有根树数量，即 ${(n+1)}^{n-1}$. ### P1 定义一个长为 $n$ 的整数序列 $a$ 是好的，当且仅当我们把它升序排序（从小到大排序）后得到的序列 $b$ 满足 $\forall i\in [1,n],1\le b_i\le i$. 求长为 $n$ 的好序列 $a$ 的个数. ---- 我们证明其与 $n+1$ 个点的有标号无根树双射，即答案是 $(n+1)^{n-1}$. 构造一张图，图中有 $n+1$ 个点，标号为 $0\sim n$.对每个 $i\in [1,n]$，连边 $(i,b_i-1)$，容易证明图形成了一棵树. 在上面的排序中，我们记录每个位置的原坐标 $pos_i$.我们钦定这里的排序是稳定排序，这样容易发现 $pos_i$ 唯一. 我们给图中的每个点分配一个新的标号，其中第 $i$ 个点的新标号为 $pos_i$.特别地，$pos_0=0$. 这样我们构造了从好序列到 $n+1$ 个点的有标号无根树的一个映射，容易验证它是双射. --- 事实上，此序列被称为 Parking Function，存在一整套围绕这个主题的理论. 但限于时间关系，我们不再具体展开。 <!-- 我们将以此为契机，引入 q-analog 的概念. --> ## 杨表 ### 杨表的概念 对于划分 $\lambda \vdash n$，我们画出 $l$ 行格子，第 $i$ 行包含 $\lambda_i$ 个格子，左对齐。 每个格子中可以填入一个正整数，这个包含数的表格称为**杨表**（Young tableau）。表格没填数时这个杨表的形状称为**杨图**，用 $\lambda$ 表示。 若我们在格子中填入的数满足： - 在 $[1,n]$ 内的正整数被不重不漏地填入所有格子； - 每行、每列中的数都严格单调递增。 则这样的杨表被称为**标准杨表**（standard Young tableau）。 ---- 若我们在格子中填入的数满足每**列**中的数**严格**单调递增且每**行**中的数**非严格**单调递增， 则称为**半标准杨表**（semistandard Young tableau，也称列严格杨表）。 **斜杨表**（skew Young tableau）定义为两个有包含关系的杨表的差集，但是我们这里不会讨论它。 ### 勾长公式 对于杨表中的某个格子 $x$，我们记其臂长为其正右方的格子数，腿长为其正下方的格子数，勾长为臂长加腿长加一，记为 $\text{hook}(x)$。 我们证明：**形状为 $\lambda\vdash n$ 的杨表个数为 $n!$ 除以每个格子的勾长之积，即：** $$ \dim \lambda = \dfrac{n!}{\prod_{x\in\lambda}\text{hook}(x)} $$ --- 这里给出勾长公式的一个概率证明。事实上，勾长公式存在直接的组合证明，但是非常复杂。 我们设 $C(\lambda)$ 为所有 $\lambda$ 中勾长为 $1$ 的“边缘”格子。对于一个 $x\in C(\lambda)$，记 $\lambda\backslash x$ 为从 $\lambda$ 中删去 $x$ 这个格子后形成的杨表。 设 $f(\lambda)$ 为在 $\lambda$ 中填数的方案数，显然有 $f(\lambda)=\sum_{x\in C(\lambda)} f(\lambda\backslash x)$。我们再令 $g(\lambda)=\dfrac{n!}{\prod_{x\in\lambda}\text{hook}(x)}$，定义 $f(\varnothing)=g(\varnothing)=1$，归纳地证明 $g(\lambda)=\sum_{x\in C(\lambda)} g(\lambda\backslash x)$ 即可。这等价于： $$ \sum_{u\in C(\lambda)}\dfrac{g(\lambda\backslash u)}{g(\lambda)}=1 $$ --- 考虑用概率论视角重新观察这个问题，可以想象我们需要构造的随机过程的大致形式是： > 从某个地方开始进行总会停止的随机游走，当且仅达到达边缘格 $u$ 时停止，$\dfrac{g(\lambda\backslash u)}{g(\lambda)}$ 就是停止在 $u$ 处的概率。 --- 若 $u$ 是 $(a,b)$ 这个格子，考虑做一些代数推理：（记 $(x,y)$ 的勾长为 $H_{x,y}$） $$ \begin{aligned} \dfrac{g(\lambda\backslash u)}{g(\lambda)} &=\dfrac{1}{n}\times\dfrac{\prod_{x\in\lambda} \text{hook}(x)}{\prod_{x\in(\lambda\backslash u)} \text{hook}(x)}\\ &=\dfrac{1}{n}\times\prod_{i=1}^{a-1}\dfrac{H_{i,b}}{H_{i,b}-1}\prod_{i=1}^{b-1}\dfrac{H_{a,i}}{H_{a,i}-1}\\ &=\dfrac{1}{n}\times\prod_{i=1}^{a-1}\left(1+\dfrac{1}{H_{i,b}-1}\right)\times \prod_{i=1}^{b-1}\left(1+\dfrac{1}{H_{a,i}-1}\right)\\ &=\dfrac{1}{n}\times\sum_{A\subseteq[a-1],B\subseteq[b-1]}\prod_{i\in A}\dfrac{1}{H_{i,b}-1}\prod_{j\in B}\dfrac{1}{H_{a,i}-1} \end{aligned} $$ $(1+\cdots)(1+\cdots)$ 显然不可能有合理且直接的概率意义，所以我们要把它打开成枚举集合。 --- 频频出现的 $\dfrac{1}{H_{x,y}-1}$ 可以被解释为从 $(x,y)$ 出发，随机走到其“勾”上除了自己外的任意一个格子，$\dfrac{1}{n}$ 大概就是随机选起始点。这个随机过程已经有些眉目了： - 在 $n$ 个格子中均匀随机地选择一个作为初始位置； - 每次从自己的“勾”中除去自己以外的 $\text{hook}(x)-1$ 个格子中均匀随机地选择一个走向它； - 走到勾长为 $1$ 的格子时停止过程。 我们只需要解释为什么走到一个格子 $(a,b)$ 处停止的概率就是上式了。 --- 容易猜想上面的 $A,B$ 分别枚举了随机游走过程中经过的行和经过的列，且： - 从一个位置 $(x,y)$ 出发开始随机游走，到达边缘格 $(a,b)$ 结束，且经过的行集合为 $A\cup \{a\}$，经过的列集合为 $B\cup \{b\}$。 在 $x\le a\land y\le b$ 时，该事件发生的概率为：$p(A,B)=\displaystyle\prod_{i\in A}\dfrac{1}{H_{i,b}-1}\prod_{j\in B}\dfrac{1}{H_{a,i}-1}$. --- 显然 $x=\min(A\cup \{a\}),y=(B\cup \{b\})$，所以只需证明上述结论即可。 依旧采用归纳的方式，$A=\varnothing$ 或 $B=\varnothing$ 的情况是显然的。对于其余情况，可以写出： $$ p(A,B)=\dfrac{p(A\backslash\{x\},B)+p(A,B\backslash\{y\})}{H_{x,y}-1} $$ 由于 $H_{x,y}-1=(H_{x,b}-1)+(H_{a,y}-1)$，直接打开即可验证上述结论正确。证毕。 --- 值得一提的是，上面的随机过程被称为 Hook Walk，另有一些应用。 比如，Hook Walk 中“均匀随机地选择”可以改为带权选择，上述结论在带权后依然成立。这可以解决一类偏序集上随机游走的问题。 --- 此外，前面提到的半标准杨表（列严格杨表）也有勾长公式： - 设值域为 $[1, m]$，在杨图 $\lambda$ 中填数形成半标准杨表的方案数为： $$ \prod_{p=(x,y)\in\lambda} \dfrac{m+y-x}{\text{hook}(p)} $$ 证明复杂，可见 IOI2019 集训队论文。 ### RSK 算法和 k-LIS/LDS 问题 杨表和排列间存在紧密的联系，比如我们有： $$ \sum_{\lambda\vdash n} \dim^2_{\lambda}=n! $$ 证明该结论就需要引入 **RSK 插入算法**。 RSK 算法的过程是根据一个排列生成其对应的两个杨表。在很多情况下，RSK 算法并不会被我们直接实现到代码里，而仅是作为理论研究的工具。 --- 对于排列 $p$，维护两个杨表 $P,Q$，分别称为该排列的**插入表**（insertion tableau）和**记录表**（recording tableau），初始均为空。 依次插入 $p_{1\cdots n}$，假设当前插入 $x=p_i$： 1. 维护一个指针 $t$，初始 $t=1$； 2. 找到 $P$ 中第 $t$ 行最小的比 $x$ 大的数 $y$； 若不存在则把 $x$ 放到本行末尾，并跳至第 4 步； 1. 交换 $x,y$，令 $t$ 自增 $1$，回到第 2 步处理下一行。 2. 对于此步在 $P$ 中新增的格子，在 $Q$ 中也新增这样一格，标上 $i$。 显然 $P$ 和 $Q$ 形状相同，且是合法的杨表。 --- 证明 $(P,Q)$ 可以唯一对应一个 $p_{1\cdots n}$，也即构造从 $(P,Q)$ 倒着推出 $p$ 的过程。 这是简单的：倒着操作，对于每个 $i$，记录表给出了 $p_i$ 及其所在的位置，凭此倒着向上恢复到插入 $p_i$ 前的状态即可。也就是说，**RSK 的单次插入是可逆的**。 --- 可以发现，RSK 算法中插入表的第一行就是我们熟知的 $O(n\log n)$ 求 LIS 的算法。这也引出了 $k$-LIS / $k$-LDS 子序列问题： - 求 LIS / LDS 长度不大于 $k$ 的子序列长度最大值。 - 由 Dilworth 定理可见这等价于"求 $k$ 条不相交的 LDS / LIS 子序列长度之和的最大值"。 但为与一般定义统一，这里采用前一种定义，也即 1-LDS 就是在求 $p$ 的 LIS 长度。 我们以 $k$-LDS 为例（不难发现 $k=1$ 时即求 LIS 长度），答案是，若 $p$ 的插入表 $P$ 的形状为 $\lambda$，则答案为 $\sum_{i=1}^k\lambda_i$，**不过构造不能直接取杨表的前 $k$ 行**。 我们将在接下来的高德纳等价一节中证明这个性质。 --- 回归视线，为了证明最开始的 $\sum_{\lambda\vdash n} \dim^2_{\lambda}=n!$，还需证明 $(P,Q)$ 可以唯一对应一个 $p_{1\cdots n}$，也即构造从 $(P,Q)$ 倒着推出 $p$ 的过程。 这是简单的：倒着操作，对于每个 $i$，记录表给出了 $p_i$ 及其所在的位置，凭此倒着向上恢复到插入 $p_i$ 前的状态即可。也就是说，**RSK 的单次插入是可逆的**。 这个唯一对应关系被称为 **Robinson–Schensted 对应**（Robinson–Schensted correspondence），记为 $p\to (P,Q)$。 --- 不加证明地给出它的一些性质：（设 $p\to (P,Q)$） - $p^{-1}\to (Q,P)$. - 由上述结论立刻得到，当且仅当 $p$ 是对合，则 $P=Q$. 这个结论并不像你想象中的那么不起眼，因为这意味着**对合与标准杨表双射**！立刻给出： $$ \sum_{\lambda\vdash n} \dim_{\lambda}=\sum_{k=0}^{n/2}\binom{n}{2k}(2k-1)!! $$ 上式的意义是枚举哪些位置是不动点。当然对合的数量也可以通过数列 $a_n=a_{n-1}+(n-1)a_{n-2}$ 计算。 --- - $(p_n,p_{n-1},\cdots,p_2,p_1)\to(P^T,Q')$，其中 $P^T$ 就是 $P$ 的转置， 而 $Q'$ 和 $P,Q$ 在形式上没什么特别的关系，不过人们发现 $Q'$ 只和 $Q$ 有关，与 $P$ 的取值独立。 - 立刻得到，对偶地，对于 k-LIS 问题，答案就是杨表前 $k$ 列的长度之和。 - $p_i>p_{i+1}$ 当且仅当 $i$ 在 $Q$ 中所在的位置 $(x_i,y_i)$ 和 $i+1$ 在 $Q$ 中所在的位置 $(x_{i+1},y_{i+1})$ 满足 $x_i<x_{i+1}$。 这也即 $p_i$ 越小，在插入过程中越容易走到更下面。 --- RSK 算法还可以推广到广义置换上，不过限于篇幅，这里不再展开。 有关排列、置换、划分问题实在是太困难了，至今为止仍没有类似于一般组合问题中的生成函数一样强大、机械、透彻的代数方法。 可以说，杨表配合 RSK 算法一起，对排列的一些性质（LIS / LDS / 下降集合）作了一定的统一。尽管研究杨表并不容易，但是这至今仍是我们研究排列问题所能利用的最先进的武器之一。 除此以外，杨表在格路计数等一众领域都有独特的应用，请同学自行了解。 ### 证明 比对一下我们可以发现只有两条不平凡的性质没有证明过： 1. $p^{-1}\to (Q,P)$； 2. $(p_{n},p_{n-1},\cdots,p_1)\to (P^T,Q')$； 第二条相当难证，此处按下不表。 --- <!-- 我们先来证明第二条中为什么是 $P^T$。 归纳法，已知 $p_{1\cdots n-1}\to (P,Q)\Rightarrow p_{n-1\cdots 1}\to (P^T,Q')$。我们设在插入 $p_n$ 时，插入过程经过了 $(1,c_1),(2,c_2),\cdots,(k,c_k)$ 这些位置，并把格子中的数依次后移了一格，最后在 $(1,c_1)$ 处填上 $p_1$。 考虑在当前 $p_{n-1\cdots 1}$ 的最前面放入一个 $p_n$ 会给杨表 $P^T$ 造成什么影响。 --- --> 我们介绍一个概念，称为 **Viennot 几何解释**（Viennot Geometric Construction）。 对于一个第一象限中的坐标 $(u,v)$，我们称 $\{(x,y)\mid x\ge u,y\ge v\}$ 这个点集为其**影子**。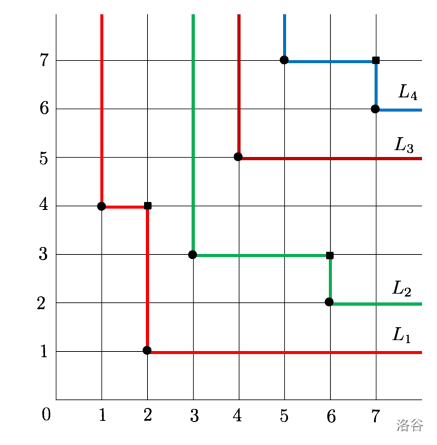 对于集合 $S$，把所有 $(x,y)\in S$ 的影子求并，称影子的边界为**影线**（shadow line） $L_1$。显然，影线是一条折线，由阶梯状的一些线段和边缘处的两条射线组成。这两条射线一条平行于 $x$ 轴，一条平行于 $y$ 轴，分别记为 $y=y_{L_1}$ 和 $x=x_{L_1}$。 --- 定义一个点集 $S$ 的**影图**（shadow diagram）$L_{1\cdots k}$： - 取出 $S$ 的影线 $L_1$。 - 把 $S$ 中**在 $L_1$ 上的点**删去，得到 $S_1$。 - 取出 $S_1$ 的影线 $L_2$。 - 把 $S_1$ 中在 $L_2$ 上的点删去，得到 $S_2$。 - 以此类推生成 $L_{1\cdots k}$，直至 $S_k=\varnothing$ 时停止。 显然 $L_i$ 两两不交且 $x_{L_i}=\min_{(u,v)\in S_{i-1}} u,y_{L_i}=\min_{(u,v)\in S_{i-1}} v$。 --- ![](https://cdn.luogu.com.cn/upload/image_hosting/wy5un6cx.png) --- 观察能力强的同学可能可以发现，插入表 $P$ 的第一行 $P_{1,i}$ 等于 $y_{L_i}$，记录表 $Q$ 的第一行 $Q_{i,1}$ 等于 $x_{L_i}$。证明可以归纳后模拟 RSK 算法的过程，有些繁琐因此略去。 那么如何刻画之后的行的性质呢？自然地，我们猜想它们也是某些折线的 $x_{L'_t},y_{L'_t}$。更仔细地研究可以得到： 定义 $(u,v)$ 是折线 $L_i$ 的**东北角**当且仅当 $(u,v)\in L_i$ 但 $(u+1,v)\notin L_i\land (u,v+1)\notin L_i$。我们取出所有 $L_{1\cdots k}$ 的东北角组成集合 $T$，求 $T$ 的影图 $L'_{1\cdots k'}$，可以发现 $x_{L'_t},y_{L'_t}$ 分别就是 $P_{2,t},Q_{2,t}$。对于第三行以后的情况同理。 证明同样考虑模拟 RSK 算法的过程，不再赘述。 --- 立刻可以解释为什么 $p^{-1}\to (Q,P)$：把所有 $(i,p_i)$ 沿直线 $y=x$ 对称即可得到 $(i,p^{-1}_i)$，那么整个几何解释也就沿着 $y=x$ 对称了。而 $P,Q$ 分别是几何解释中关于 $x,y$ 的信息，自然也就变成 $(P,Q)$ 了。 ### 高德纳等价 给定 $n$ 阶排列 $p_{1\cdots n}$，你可以执行任意多次（包括 $0$ 次）以下操作： - 选择整数 $i\in [1,n)$，满足存在 $x\in \{i-1,i+2\}$ 使得 $1\le x\le n$ 且 $\min(a_i,a_{i+1})<a_x<\max(a_i,a_{i+1})$。 然后交换 $a_i,a_{i+1}$。 问有多少本质不同的排列可以由这种操作得到，答案模 $998244353$。 --- 首先有： ![](https://xyix.github.io/images/nytoi-2021-d.png) --- 因此假如两派列等价，则他们在 RSK 算法中的插入表应当相同。不难猜测此条件同样充分，即：**所有插入表相同的排列应当等价**。 如何证明之？需要引入一个概念： > 定义一个杨表 $\lambda$ 的**阅读词**（reading word） 为把此杨表从下往上、从左往右地读出每行的结果，记做 $\text{read}(\lambda)$。 容易证明 $\text{read}(\lambda)$ 的插入表恰为 $\lambda$，接下来按 $n$ 的大小归纳证明任意排列和它对应的插入表的阅读词等价。 --- 考虑一个长为 $n+1$ 的排列，把其前 $n$ 位插入杨表中得到近似标准杨表 $\lambda$。 由归纳假设，前 $n$ 位和 $\text{read}(\lambda)$ 等价，现在插入第 $n+1$ 位上的数 $k$，只需证 $\text{read}(\lambda^\prime)\sim \text{read}(\lambda)+k$。 考虑第一行，只需把 $\text{read}(\lambda)+k$ 中的 $k$ 不断往前移动，易证一定可以移至正确位置（即前面的数 $<k$，后面的数 $>k$），但 $\lambda^\prime$ 中 $k$ 不一定在第一行，不能直接这样移动。 --- 分类讨论： - 如果一次都移动不了，那么显然 $\text{read}(\lambda)+k=\text{read}(\lambda^\prime)$，无需移动。 - 否则我们不断把 $k$ 向前移动，直到它再移动一次就没法移动了。 此时第一行中一定是 $\cdots(<k)(<k){\color{red}(>k)}(k)(>k)(>k)\cdots$ 的状态，而且在 RSK 过程中标红的这个 $>k$ 的数应该继续向下插。 我们把这个数向前移动至 ${\color{red}(>k)}(<k)\cdots(<k)(<k)(k)(>k)(>k)\cdots$ 的状态，这样在阅读词中 $>k$ 的这个数等价于在第二行末尾，应用归纳假设即可。 证毕。这种等价关系被我们称为**高德纳等价**（Knuth-equivalence）。 --- 我们再来证明杨表和 k-LDS 之间的联系。（注意上面的构造没有利用 k-LDS 和杨表间的关系，所以没有循环论证！） 首先，对于每个排列 $p\to (P,Q)$，它都可以在不改变 k-LDS 长度、且不改变插入表的前提下变化到 $\text{read}(P)$，那么我们只需要证明 $\text{read}(P)$ 的 k-LDS 长度是 $\sum_{i=1}^k\lambda_i$ 即可。 构造是显然的，直接取前 $k$ 行即可，证明最值只需要注意到每列中至多只能选择 $k$ 个元素即可。 ### 一个经典问题 > 求把 $n$ 个点的多边形划分成 $k$ 个部分的方案数，不考虑旋转、翻转同构，保证 $n\ge 3, k\le n-2$。 > 形式化地，"划分成 $k$ 个部分"指在 $n$ 个顶点间连 $k-1$ 条边，使得无重边、无自环且任意两边只在顶点处相交。 ---- 答案是： $$ \dfrac{1}{k}\binom{n-3}{k-1}\binom{n-2+k}{k-1} $$ 随便定一条基准边，从基准边出发递归下去划分子树，将原问题双射到一棵 $n-1$ 个叶子点，$k$ 个非叶子点的树. 在每个叶子上标上 $-1$，非叶子点上标上 (儿子数 $-1$). 根据 DFS 序记录序列，**再剔除最后一个叶子**得到 $a_{1\cdots n+k-2}$，满足： - $n-2$ 个元素为 $-1$，其余元素为正，总和为 $0$； - 每个前缀和非负. 可以简单证明这与原问题双射. --- 我们再证明这个东西和 $(k,k,1,1,\cdots,1)$ 的杨表双射，其中 $1$ 有 $n-k-2$ 个. 记 $a$ 中正数序列是 $b_{1\cdots k}$，我们从 $1\cdots n+k-2$ 一个一个地往杨表里填数： - 若 $a_i\ge 1$，把 $i$ 塞到当前的第一行末尾； - 否则 $a_i=-1$，设在这次之前出现过 $z$ 个 $-1$： - 若 $\exists j\in [0,k], \sum_{t=1}^j b_j=z$，则把 $i$ 塞到当前的第二行末尾； - 否则把 $i$ 塞到当前的第一列末尾；（两种操作等价当且仅当 $z$ 为 $0$，因此不用担心） 从杨表倒着生成 $a$ 可以先把正数的位置确定好，然后根据负数区出现数的位置确定每个正数. 于是双射就完成了. 不难发现杨表里有 $n+k-2$ 个数，由勾长公式，答案为： $$ \dfrac{(n+k-2)!}{\prod_x \text{hook}(x)}=\dfrac{(n+k-2)!}{(n-1)(n-2)\times (n-k-2)!\times k!\times (k-1)!} $$ 这就是上面那个式子了. ### ZJOI 2022 D2T2 > 九条可怜是一个喜欢计算几何的女孩子，她画了一个特别的平面坐标系，其中 $x$ 轴正半轴与 $y$ 轴正半轴夹角为 $60$ 度。 > 从中，她取出所有横纵坐标不全为偶数，且满足 $-2 a + 1 \le x \le 2 a - 1$，$-2 b + 1 \le y \le 2 b - 1$，$-2 c + 1 \le x + y \le 2 c - 1$ 的整点。 > 可怜想将其中一些点染色，但相邻的点不能同时染色。具体地，对于点 $(x, y)$，它和 $(x, y + 1), (x, y - 1), (x + 1, y), (x - 1, y), (x + 1, y - 1), (x - 1, y + 1)$ 六个点相邻，可结合样例解释理解。 > 可怜想知道在这个规则下最多能将多少点染色，以及染最多点的染色方案数。由于后者值可能很大，对于染色方案数，你只需要输出对 $998244353$ 取模后的结果。**注意不需要将最多染色点数取模。** > 多测，$T\le 10,1\le a,b,c\le 10^6$。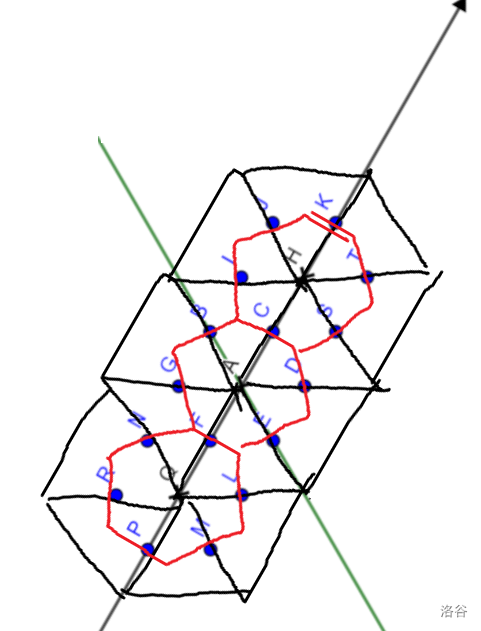 --- 我们先把限制在 $90^\circ$ 坐标系内画出来，然后拉伸，发现合法区域大概是一个六边形. 这个限制条件十分阴间，我们考虑一下能不能双射到一个人类能接受的结构. 事实上，有一个非常反人类的双射，可以把它射到六边形战士那个三角形匹配，大致过程是把这个东西点化边： --- ![](https://cdn.luogu.com.cn/upload/image_hosting/yhowg29l.png) --- 这样这个题中选不相邻的点就是原题中的选不相邻的边，也就是完美匹配. 现在考虑第一问答案是啥. 有一些退化情况，比如如果 $c\ge a+b$ （及其对称情况），图形就会退化为菱形，那么可以算出答案就是 $4ab$，且只有一种情况. 这点归纳一下可以证明，细节可能有点恶心. 否则问题就转化为三角形匹配，我们要得到六边形的六条边分别有多长，我们发现，相邻的三条边边长分别是 $a+b-c$ 的对称式. 三角形最大匹配的值就是三角形数量，这怎么求？可以补成一个平行四边形. --- 然后怎么做？旋转一下把他们看作是正方体堆叠，长、宽、高分别是 $a,b,c$. 那么我们可以考虑描绘出每个高度的轮廓线，不难发现这也是双射. 这就可以 LGV 了：$A_{i,j}=\dbinom{a+b}{a+i-j}$，求一个行列式. 这个东西可以代数化简，但是依托答辩，更优雅的做法是利用半标准杨表. --- 和小学中表示一个立体图形类似，我们在俯视图上每个格子标出其数目，这样只要满足： - 每个数都在 $[0,c]$ 之间. - 每行、每列单调不增. 即可. 但是这没法直接转化为杨表，我们可以对每行加 $1$，双射到值域 $[1,a+c]$ 之间的半标准杨表. --- 然后由半标准杨表的计数公式： $$ f_{\lambda}=\prod_{(i,j)\in \lambda}\dfrac{m+j-i}{h_{\lambda}(i,j)} $$ 答案就是： $$ \prod_{1\le i\le a}\prod_{1\le j\le b} \dfrac{a+c+j-i}{a+b-i-j+1} $$ 分母是 $$ \prod_{0\le i<a}\prod_{1\le j\le b}(i+j)=\prod_{0\le i<a}\dfrac{(i+b)!}{i!}=\dfrac{F(a+b-1)}{F(a-1)F(b-1)} $$ 其中 $F(x)=\prod_{i\le x}i!$. 分子也可以类似计算。 ## Good Luck & Have Fun！