CSP 数学基础
ollie
2019-11-08 10:53:21
## CSP 数学基础
### 整理&修改—— ollie 
#### 说明:蒟蒻只是整理,供自己和同学学习,部分转载其他博客,有一些链接丢失,如果有补充请在评论区@,会补上链接。
#### 你可能会好奇为啥要转载,因为我懒的一个一个找了。。。
- 取模相关
- 素数判断
- GCD/EXGCD
- 欧拉函数
- 欧拉定理
- 扩展欧拉定理
- 逆元
- 同余公式
- 逆元求法
- CRT/EXCRT
- 线性代数
- 快速幂
- *矩阵相关
- *高斯消元
- 组合数学
- 卡特兰数
- 排列组合
- 二项式定理
- 杨辉三角
- Fibonacci数列
- *Lucas定理
- 数学期望
- [原博客(目录)]( https://blog.csdn.net/M_oisture/article/details/83820851 )
先来一个跟我讲的毫无干系的[例题](https://www.luogu.org/problem/P1403)
### 一、取模相关
- `n%p`所得结果的正负由`n`决定,与`p`无关。如:`7%4=3`,`-7%4=-3`,`-7%-4=-3`
- 欧拉定理(后面会细讲)
$$
α^{\varphi(p)}≡1mod(p)
$$
- 当p为质数的特殊情况
$$
α^{p-1}≡1
$$
- Noip2014式取模, 如果f(x) = 0, 那么f(x) % p = 0, 在式子中带入数字看脸计算。
- 常数较小的取模方式
### 二、素数判断
1:一般筛法(埃拉托斯特尼筛法):
基本思想:素数的倍数一定不是素数
~~应该没人用咱就跳过吧~~
```cpp
#include<cstring>
#include<cmath>
const int MAXN=1000010;//范围
bool prime[MAXN];
void make_prime()
{
memset(prime,true,sizeof(prime));
prime[0]=prime[1]=false;
int t=sqrt(MAXN);
for(register int i=2;i<=t;i++)
{
if(prime[i])
{
for(register int j=2*i;j<MAXN,j+=i)
{
prime[j]=false;
}
}
}
return;
}
```
此方法的复杂度为
$$
O(\sum_{p<n}\frac{n}{p})=O(nloglogn)
$$
2:线性筛(优化)
原理:初始时,假设全部都是素数,当找到一个素数时,显然这个素数乘上另外一个数之后都是合数,把这些合数都筛掉,即算法名字的由来。
```cpp
#include<iostream>
using namespace std;
const int N = 200000;
int prime[N] , num_prime;
int isNotPrime[N] = {1, 1};//先将0,1排除,合数
int main()
{
for(int i = 2 ; i <= N ; i ++)
{
if(! isNotPrime[i]) //isNotPrime==0,即不是合数
prime[++num_prime]=i;//素数++,这不是关键1
//关键处1
/*i为合数时也要参与循环*/
for(int j = 1; j <= num_prime&&i * prime[j] <= N ; j ++)
/*i乘以其它质数=合数,且质数比自己小或者是自己(已经求出来了),所以不可能重复*/
{
isNotPrime[i * prime[j]] = 1;//乘以其它素数得到的一定是合数,之所以不重复是因为质数间不等
if( !(i % prime[j] ) ) //关键处2 如果i是p的倍数,退出循环,这样可以保证一个数只会被最小素因子筛到一次,prime是从小到大枚举的,1067=11*97,
break;
}
}
return 0;
}
```
先,先明确一个条件,任何合数都能表示成一系列素数的积。(为啥???)
$4 = 2 * 2$ , $12 = 2 * 3 * 3$, .......
不管 i 是否是素数,都会执行到“关键处1”( 别看错啦),
①如果 i 都是是素数的话,那简单,一个大的素数 i 乘以不大于 i 的素数,这样筛除的数跟之前的是不会重复的。筛出的数都是 N=p1*p2的形式, p1,p2之间不相等 ( 素数不会与其他数相等 )
$77=7*11$ , 即 $77$ 只能化简成这个形式且唯一 ( ~~这要是不懂那我也木得门~~ )
②如果 i 是合数,此时 i 可以表示成递增素数相乘 $i=p1* p2 * ...*pn$, $pi$都是素数$(2\leq i\leq n)$, $pi\leq pj ( i\leq j )$
p1是最小的系数。
根据“关键处2”的定义,当$p1==prime[j]$ 的时候,筛除就终止了,也就是说,只能筛出不大于p1的质数。
我们可以直观地举个例子。$i(235)=2*3*5 = 5 * 47$
$for\,\, j=1 -> num\,prime j = 1,2,3,4,5,....$
此时能筛除 $2i(470)$ ,不能筛除 $3i(705)$
如果能筛除$3i$ 的话,当 $i'$ 等于 $i'=335$ 时,筛除$2 * i'(705)$就和前面重复了。
所以只能枚举到最小质因子
##### 质数应用
- 用来取模
- ~~用来装 B~~
[P2312 解方程](https://www.luogu.org/problem/P2312)
### 三、GCD&EXGCD
#### 1 . gcd:
欧几里得算法,即辗转相除法,简称gcd,用于计算两个数的最大公约数。
公式 :
$$
gcd(a,b)=gcd(b,a mod b) ,b≠0
$$
啥?证明?能用就行要什么证明
咳咳,让我们来严格的证明一下
> 若 $a < b$,以上等式显然成立(~~你这要是不会我也没办法~~)#1
>
> 若 $a \geq b$, 设$a = q *b + r,0\leq r<b$, 即r=a%b 。对于$a$,$b$的任意公约数$d$,因为$d|a$(ps:这个符号的意思是d是a的约数),$d|b$,所以$d|(q * b)$, 可得$d|(a-q*b)$#2,即$d|r$,$d$也是$r$的约数。反之亦成立。所以,$a$,$b$的公约数集合和$b$,$a mod b$的公约数集合相同,他们的最大公约数自然也相同。
>
> 证毕
~#1解释:$gcd(10,20)=gcd(20,10\bmod20)=gcd(20,10)$[~~竟然看这个~~]
~#2解释:为什么?因为$d|a$,$d|b$可以写成$a=k1*d,q*b=k2*d$,相减得$a-q*b=(k1-k2)*d$即是d的倍数
上代码(~~我知道你们只想要这个~~)
```cpp
int gcd(int a,int b){
return b?gcd(b,a%b):a;
}
```
##### 补充:
**如何求 $lcm(i,j)$?**
提醒你:
$$
lcm(i,j)=\frac{i*j}{gcd(i,j)}
$$
也就是说gcd求出来lcm也就求出来了。。。
[上题](https://www.luogu.org/problem/SP5971)
#### 2 . exgcd:
用于求逆元
引理:**裴蜀定理**,一定存在$ax+by=gcd(a,b)$的整数解
乱证严格的证明:
> 当$b=0$时,$gcd(a,b)=a$,显然存在一对整数解$x=1,y=0$
>
> $gcd(10,0)=10$
>
> 若$b\neq0$
> 设$ax1+by1=gcd(a,b)=gcd(b,a \bmod b)=bx2+(a\bmod b)y2$
>
> 又因 $a\bmod b=a-a/b*b$
>
> 则 $ax1+by1=bx2+(a-a/b*b)y2$
>
> $ax1+by1=bx2+ay2-a/b*by2$
>
> $ax1+by1=ay2+bx2 -b* a/b * y2$
>
> $ax1+by1=ay2+b(x2-a/b*y2)$
>
> 解得 $x1=y2 , y1=x2-a/b*y2$
>
> 因为当 $b=0$ 时存在 $x , y$ 为最后一组解
>
> 而每一组的解可根据后一组得到
>
> 所以第一组的解 $x , y$ 必然存在
~~你要是不懂那就背吧~~
那么就到了激动人心的代码时间啦
求:
$$
ax\equiv1\pmod{b}
$$
$$
ax\bmod b =1 ->ax + by = 1
$$
原理是,方程 $ax + by = m$有解的必要条件是 $m \bmod gcd(a,b) = 0$
这个简单证一下。
由最大公因数的定义,可知 $a$ 是 $gcd(a,b)$ 的倍数,且 $b$ 是 $gcd(a,b)$ 的倍数,
若 $x,y$ 都是整数,就确定了 $ax + by$ 是 $gcd(a,b)$ 的倍数,
因为 $m = ax + by$,所以 $m$ 必须是 $gcd(a,b)$ 的倍数,
那么 $m \bmod gcd(a,b) = 0$
蒟蒻版:
```cpp
void exgcd (ll a, ll b, ll &x, ll &y)
{
if (b == 0) {
x = 1;
y = 0;
return ;
}
exgcd (b, a % b, x, y);
ll tmp = x;//#1此时的x=x2,y=y2,tmp = x2
x = y;//x 存储答案
y = tmp - a / b * y;//y1 = x2 - a/b*y2
//推上一个y1,从下往上推
}
```
萌新版:
```cpp
#include <bits/stdc++.h>
#define int long long
using namespace std;
int x, y, a, b;
void exgcd(int a, int b, int &x, int &y)
{
if(b) exgcd(b, a%b, y, x), y-=(a/b)*x;//压缩,不会自己thinkthink
//敲黑板(重点)exgcd(y,x)不是(x,y)
else x=1,y=0;
}
signed main()
{
scanf("%lld%lld",&a,&b);
exgcd(a,b,x,y);
printf("%lld",(x%b+b)%b);//x为逆元
return 0;
}
```
### 四、欧拉函数( 浅谈 )
#### **1、积性函数**
###### 概念
> 积性函数是对数论中一系列有特殊性质函数的统称,性质如下:
> 若
> $$
gcd(a,b)=1, f(ab)=f(a)f(b)
$$
> 那么 f 则是积性函数
>
> 特别地,假如对于任意的a、b,即
> $$
f(ab)=f(a)f(b)
$$
> 那么称 f 为完全积性函数
#### 2、欧拉函数概念
> 定义:欧拉函数$φ(n)$表示[1,n]范围内与n互质的数的个数。
> $$
\varphi( n )= \sum_{i=1}^{n} [ gcd ( i,n ) = 1 ]
$$
#### **3、基本性质**
###### 1.对于一个质数$p$, $φ (n) = p - 1$ (相对来说用的比较多)
证明:根据质数的定义,对于任意一个不是$p$倍数的正整数$x$,总有$gcd(p,x)=1$,即$p$与$x$互质。在$1~p$之间,只有$1×p$是$p$的倍数,故在1~p中,与$p$互质的数为$1$到$p-1$,共$p-1$个,$\varphi(p)=p-1$。
###### 2.对于一个质数p,
$$
\varphi(n) = p^{k}-p^{k-1}=p^{k-1}*(p-1)=p^{k-1}*\varphi(p)
$$
证明:我们知道,在 1~p 之间与 p 不互质的数共1个,在 1~2×p 之间与 p 不互质的数共2个……在1~p^(k−1)×p 之间有 p^(k−1) 个。所以在 1~p^k 之间与 p 不互质的数有 p^(k−1) 个,互质的那就是p^(k)−p^(k−1),故φ(p^k)= p^k−p^(k−1),即第二个式子。然后提取公因数 p^(k−1) 得到第三个式子。结合性质1得到第四个式子。
###### 3.对于一个数n,我们将其质因数分解为
$$
n=\prod_{i=1}^{k}p_{i}^{ri}
$$
###### 那么
$$
\varphi(n)=\prod_{i=1}^{k}\varphi(p_{i}^{ri})=\prod_{i=1}^{k}p^{ri-1}*(p-1)=n*\prod_{i=1}^{k}(1-\frac{1}{pi})
$$
**这个就是 _唯一分解定理_ 了**
证明:由于欧拉函数有积性,$φ(ab)=φ(a)φ(b)$,所以有
$$
\varphi(n)=\prod_{i=1}^{k}\varphi(p_{i}^{ri})
$$
结合性质2的第三个式子,我们可以得到第三个式子。对于第三个式子,我们提取一个公因子p,得到
$$
\prod_{i=1}^{k}p_{i}^{ri}*(1-\frac{1}{pi})=(\prod_{i=1}^{k}p^{ri})*(\prod_{i=1}^{k}(1-\frac{1}{pi}))=n*\prod_{i=1}^{k}(1-\frac{1}{pi})
$$
得证。
#### 4、扩展性质( 不证明 )
###### 1.假如$a,b$不互质,那么$φ(ab)$等于什么呢?
结论:令$d=gcd(a,b)$,则
$$
\varphi(ab)=\frac{\varphi(a)\varphi(b)d}{\varphi(d)}
$$
###### 2.对于任意正整数$n$,$φ(n)$与$n$有什么样的关系?
结论:
$$
n=\sum_{d|n}\varphi(d)
$$
#### 5、欧拉函数求法
① 直接求单独的phi值(只求某一个)
原理:质因子分解(基本性质3)。每次找到一个素因子,之后把它”除干净“,即可保证找的因子全部都为素数(这个比较容易理解,从2开始进行循环,删除二的所有倍数,因为含有倍数,则必定不是素数,从而确保下次循环所选的数必定为素数,额…若仍不理解,可以自己打表看一下,而事实也确实如此)。
```cpp
int phi(int n){
int ans=n,m=(int)sqrt(n+0.5);//细节问题,自己thinkthink
for(int i=2;i<=m;i++){//筛选素因子
if(n%i==0){//i必为素数(为什么,自己thinkthink)
ans=ans/i*(i-1);
while(n%i==0) n/=i; //每次都将素数因子除干净,这样就保证了每次寻找的i均为素数。均在唯一式内
}
}
if(n>1) ans=ans/n*(n-1);//若n不为1,则说明还有素数未除,则是n本身,继续进行上面的操作
return ans;
}
```
② 线性筛 (咋又是它嘞)
由于欧拉函数有积性,所以结合扩展性质1:
令$d=gcd(a,b)$,则
$$
\varphi(ab)=\frac{\varphi(a)\varphi(b)d}{\varphi(d)}
$$
我们可以通过线性筛质数,在筛出合数 $x * pri[j]$ 的同时计算出 $φ( x*pri[j] )$。(注:$pri[j]$ 为已经筛出来的质数,见上面的线性筛 )
不过,需要分2种情况计算:
1. **$x$ 与 $pri[j]$ 互质.**
这种情况比较简单。由于$d=1$,$φ(d)=1$,所以
$$
\varphi(x*pri_{j})=\varphi(x)*\varphi(pri_{j})
$$
直接计算即可
2. **$x$ 与 $pri[j]$ 不互质.**
这种情况下,$x$ 只可能是 $pri[j]$ 的倍数,故$ d = gcd( x, pri[j] ) = pri[j]$,根据扩1,所以:
$$
\varphi(x*pri_{j})=\frac{\varphi(x)\varphi(pri_{j})pri_{j}}{\varphi(pri_{j})}=\varphi(x)*pri_{j}
$$
带入计算即可
所以代码就出炉啦
```cpp
#include <bits/stdc++.h>
#define int long long
#define MAXN 3005000
using namespace std;
int phi[MAXN];//储存φ值
int not_prime[MAXN];
int prime[MAXN];
int n, p, tot;
void shake_it()
{
phi[1] = 1;
for(int i = 2; i <= n; i++)
{
if(!not_prime[i])
{
prime[++tot] = i;
phi[i] = i - 1;//基本性质1
}
for(int j = 1; prime[j]*i <= n; j++)
{
not_prime[prime[j]*i] = 1;
if(i%prime[j]==0)//如果i是prime的倍数
{
phi[prime[j]*i] = phi[i] * prime[j];
break;
}
phi[prime[j]*i] = phi[i] * (prime[j] - 1);
}
}
}
signed main()
{
scanf("%lld", &n);
shake_it();//线性筛
return 0;
}
```
#### 6、欧拉定理
##### ① 概念
> 若正整数 a , n 互质,则
> $$
a^{\varphi(n)}\equiv1\pmod{n}
$$
> 其中 $φ(n)$ 是欧拉函数(1~n) 与 n 互质的数
~~证明太***就不证明了~~
##### ② 费马小定理
> 对于质数 p,任意整数 a,均满足:
> $$
a^{p}\equiv a\pmod{p}
$$
> 即两边同时除 a 得:
> $$
a^{p-1}\equiv1\pmod{p}
$$
#### 7、扩展欧拉定理
当 $a , m ∈ Z$ 时有:
$$
a^{b} = \left\{\begin{matrix}
a^{b}& , & b<\varphi(m)\\
a^{b\,mod\,\varphi(m)+\varphi(m)}&, & b\geq\varphi(m)
\end{matrix}\right.\pmod{m}
$$
证明略。
[P5091
【模板】欧拉定理]( https://www.luogu.org/problem/P5091 )
[P4139 上帝与集合的正确用法](https://www.luogu.org/problem/P4139)
### 五、逆元
#### 0、转自[Nickel_Angel's nest](https://www.luogu.org/blog/1239004072Angel/post-shuo-xue-sheng-fa-ni-yuan)
#### 1、同余公式
> (a+b)%p = (a%p + b%p) %p
>
> (a-b)%p = (a%p - b%p) %p
>
> (a*b)%p = (a%p) * (b%p) %p
推论:a^b %p = (a%p)^b %p
但是……除法?
(a/b)%p ≠ (a%p) / (b%p) %p
怎么办?
~~这个时候就要呼叫超级飞侠啦~~
#### 2、逆元定义
乘法逆元,一般用于求
$$
\frac{a}{b} \pmod p
$$
的值($p$ 通常为质数),是解决模意义下分数数值的必要手段。
~~不知道定义都不知道后面在BB啥~~
> 若
> $$
a*x\equiv1 \pmod {b}
$$
> 且a与b互质,那么我们就能定义:x 为 a 的逆元,记为
> $$
a ^{-1}
$$
>
> 所以我们也可以称 x 为 a 在 modb 意义下的倒数,
>
> 所以对于
> $$
\displaystyle\frac{a}{b} \pmod {p}
$$
> 我们就可以求出 b 在 mop 下的逆元,然后乘上 a,再 modp,就是这个分数的值了。
#### 3、逆元求法(整理[原博客]( https://www.luogu.org/blog/1239004072Angel/post-shuo-xue-sheng-fa-ni-yuan ) )
##### ① EXGCD求逆元
同上不讲。 时间复杂度为 $O(log\,\, p)$
##### ② 欧拉定理求逆元
观察式子
$$
ax \equiv 1 \pmod{p}
$$
我们发现它和欧拉定理
$$
a^{\varphi(p)} \equiv 1 \pmod{p}
$$
很像……
而欧拉定理又是 $a,p$ 互质时成立,这和逆元存在的条件相同……
故将两个式子合在一起,得:
$$
ax\equiv a^{\varphi(p)}\pmod{p}
$$
两边同时除 a 得:
$$
x\equiv a^{\varphi(p)-1}\pmod{p}
$$
故
$$
x = a^{\varphi(p)-1}mod p
$$
求出欧拉函数后,可以使用快速幂求出答案。
code:
```cpp
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
long long n, p;
long long phi(long long x)//求x的欧拉函数
{
long long res = x, tmp = x;//初始化答案为x
for (int i = 2; i * i <= tmp; ++i)
{
if (x % i == 0)
{
res = (res / i) % p * ((i - 1) % p) % p;//找到x的一个质因子,计算其对答案的贡献
while (x % i == 0) x /= i;//统计完答案后,除去该质因子
}
}
if (x > 1) res = (res / x) % p * ((x - 1) % p) % p;//防止漏筛质因子
return res;
}
long long power(long long a, long long b)//快速幂
{
long long res = 1;
while (b)
{
if (b & 1) res = res * a % p;
a = a * a % p;
b >>= 1;
}
return res;
}
int main()
{
scanf("%lld%lld", &n, &p);
long long tmp = phi(p) - 1;
printf("%lld", power(n, tmp));
return 0;
}
```
时间复杂度为:
$$
O(log\varphi(p)+\sqrt p)
$$
##### ② 费马小定理求逆元
**TIP:** 仅能在 p 为质数的时候使用
> 费马小定理:若 p 为质数,且整数 a 满足 p | a ,则有:
> $$
a^{p-1}\equiv1\pmod{p}
> $$
对于定理中的式子,我们可以将两边同除 a ,得:
$$
a^{p-2}\equiv a^{-1}\pmod{p}
$$
而 a^(-1)就是 a在模 p 意义下的乘法逆元。
故我们只需计算 a^(p-2) mod p 即可,而这个过程可用快速幂解决。
我们不妨看看最初的问题,如何对一个分数取模?
$$
x=\frac{a}{b}modp=ab^{-1}modp
$$
只需要算 b 的逆元就行啦
时间复杂度为 $O(logp)$
##### ③ 线性求逆
**TIP:** 仅能在 p 为质数的时候使用
基于拓展欧几里得算法,我们虽然可以在 O(n log p)时间内,求出 [1,n]中所有整数在模质数 p 下的乘法逆元,但在面对更大的数据范围时,我们就需要更快的方法。
首先,我们不难发现,对于任何正整数 $c$,$1 * 1^{-1} ≡ 1 (mod c)$ ,即 1 在模任意正整数意义下的逆元为其本身。然后设 $p = ki + r(r < i, 1 < i < p)$,将其转化为同余式会得到:
$$
ki+r\equiv0\pmod{p}
$$
两边同时乘 $i ^{-1}, r^{-1}$,得:
$$
i^{-1}r^{-1}(ki+r)\equiv0\pmod{p}
$$
将式子乘开:
$$
kr^{-1}+i^{-1}\equiv0\pmod{p}
$$
移项得:
$$
i^{-1}\equiv -kr^{-1}\pmod{p}
$$
由于 $p = ki + r (r < i, 1 < i <p)$ 易知 $k = p/i$(下取整), $r = p \bmod i$,故有:
$$
i^{-1}\equiv-\left \lfloor\frac{p}{i} \right \rfloor*(p\,mod\,i)^{-1}\pmod{p}
$$
而 $p \bmod i < i$ ,故 $p \bmod i$ 的逆元我们之前已经递推出来了,故我们可以通过这个式子推出 i 的逆元是谁。 最终式子为:
$$
i^{-1}\equiv(p-\left \lfloor\frac{p}{i} \right \rfloor)*(p\,mod\,i)^{-1}\pmod{p}
$$
code:
```cpp
#include <bits/stdc++.h>
#define int long long
#define MAXN 5000000
using namespace std;
int n, p;
int x, y;
int inv[MAXN];
signed main()
{
scanf("%lld%lld", &n, &p);
inv[1] = 1;
for(int i = 2; i <= n; i++)
{
inv[i] = (p-p/i)*inv[p%i]%p;
printf("%d\n", inv[i]);
}
return 0;
}
```
**TIP:** 当然还有很多的方法,这里只列举比较常用的几种求逆元的方法
[P2613 【模板】有理数取余](https://www.luogu.org/problem/P2613)
[P5431 【模板】乘法逆元2](https://www.luogu.org/problem/P5431)
### 六、CRT/EXCRT
#### 1.CRT
##### 0.转载某[大佬]( https://www.luogu.org/user/111987 )(%%%),蒟蒻修改部分
##### 1.定义:
若m[1],m[2],...,m[n] 是两两互质的正整数, $M= \prod_{i=1}^n{m[i]}$,$M[i]=M/m[i] ,t[i]$ 是线性同余方程 $M[i] * t[i] ≡1(\bmod m[i])$的一个解。对于任意的$n$个整数$a[1], a[2], a[3], ... , a[n]$,则同余方程组为:
$$
\left\{\begin{matrix}
x\equiv a_{1}\pmod{m_{1}}\\
x\equiv a_{2}\pmod{m_{2}}\\
......\\
x\equiv a_{n}\pmod{m_{n}}
\end{matrix}\right.
$$
有整数解,方程组的解为
$$
x=a_{1}M_{1}t_{1}+a_{2}M_{2}t_{2}+...+a_{n}M_{n}t_{n}
$$
并且在%M意义下有唯一解。
##### 2.证明:
因为$M[i] = M/m[i]$ 是除$m[i]$ 之外所有模数的倍数,所以 $∀$ (任意)$k \neq i$,$a[i]M[i]t[i]≡0(\bmod m[k])$.又因为 $a[i]M[i]t[i] ≡a[i] (mod m[i])$,所以代入$x$得
$$
x=\sum_{i=1}^{n}a_{i}M_{i}t_{i}
$$
##### 3.结论:
中国剩余定理给出了模数两两互质的线性同余方程组的一个特殊解。方程组的通解可以表示为$x+kM(k∈Z)$。有些题目要求我们求出最小的非负整数解,只需把x对M取模,并让x落在0~M-1的范围内即可。
```cpp
int intchina(int r)
{
int Mi,x,y,d,ans=0;
int M=1;//注意取1
for(int i=1;i<=r;i++) M*=m[i];
for(int i=1;i<=r;i++){
Mi=M/m[i];
exgcd(Mi,m[i],d,x,y);
ans=(ans+Mi*x*a[i])%M; //Mi相当于Mi,x—>ti
}
return (ans+M)%M;//防负数
}
```
[P1495 曹冲养猪](https://www.luogu.org/problem/P1495)
#### 2.EXCRT
某位神仙说提高不会考,如果考到~~我认命~~,如果实在想学可以点击[这里](https://www.luogu.org/problemnew/solution/P4777)
### 七、线性代数
#### 0.前置
线性代数比较难(矩阵)而且不咋考,~~所以就马马虎虎地走个过场~~
#### 1.快速幂
这个大家都会,我就只贴板子了
如果你实在要搞懂原理 [戳我](https://www.luogu.org/problemnew/solution/P1226)
求:
$$
a^{b}\,mod\,p
$$
code:
```cpp
ll quick_pow(ll a, ll b, ll p)//a^b mod p
{
ll t=1;
while(b)
{
if(b&1) t=t*a%p;
a=a*a%p;
b>>=1;
}
return t;
}
```
#### 2.矩阵相关
%%%大佬 **可爱即是正义**
直接使用传送术(懒得排了,也不是很重要的东西)
[可爱即是正义 的博客](https://www.luogu.org/blog/shehuizhuyihao/post-zhen-sheng-fa)
#### 3.*高斯消元
某位神级清华sang师说高斯消元noip不会考,不属于提高组,所以不讲,如果感兴趣自己下去查吧。
### 八、组合数学
#### 0.前置:
这个也是考的比较多的
#### 1.卡特兰数(卡姿兰数)
**0、说明:**
[原博客](https://blog.csdn.net/wookaikaiko/article/details/81105031)
##### 1.卡特兰数是啥:
> 卡特兰数是一种经典的组合数,经常出现在各种计算中,其前几项为 : 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
TIP:Cn,hn,fn均表示卡特兰数(在这)
##### 2.卡特兰数的公式
###### ① 递归公式1
$$
f(n)=\sum_{i=0}^{n-1}f(i)*f(n-i-1)
$$
如果我们用这个公式显然我们要使用递归算法,那么数据一大就在时空上很麻烦
###### ② 递归公式2
$$
f(n)=\frac{f(n-1)*(4*n-2)}{(n+1)}
$$
这个公式应用递推,看上起十分和善
但对大数据呢?
我们注意到大数据的时候 f(n) 会很大,这时候题目一般会让你对某素数取模(~~当然你可以打高精度~~)
但你在取模过程中难保一个 f(n)%mod=0
那么根据公式下面所有的数都会等于0,于是你就愉快的WA了
###### ③ 组合公式1
$$
f(n)=\frac{C_{2n}^{n}}{(n+1)}
$$
卡特兰数可以与组合数联系起来,得到上面的公式
而组合数就是一个杨辉三角,可以递推得到
但我们发现对于大数据你要取模,而对于除法你是没办法用膜的性质的(~~当然你可以应用逆元~~),所以造成了麻烦
###### ④ 组合公式2
$$
f(n)=C_{2n}^{n}-C_{2n}^{n-1}
$$
与组合数公式1不同这个是两个组合数的减法
减法是可以用膜的性质的,于是你可以愉快的AC了。
##### 3.卡特兰数的应用
**①、进出栈问题**:
栈是一种先进后出(FILO,First In Last Out)的数据结构.如下图1,2,3,4顺序进栈,那么一种可能的进出栈顺序是:1In→2In→2Out→3In→4In→4Out→3Out→1Out, 于是出栈序列为1,3,4,2。

**那么一个足够大的栈的进栈序列为1,2,3,⋯,n时有多少个不同的出栈序列?**
[例题]( https://www.luogu.org/problem/P1044 )
我们可以这样想,假设 x 是最后一个出栈的数。
由于x是最后一个出栈的,所以可以将已经出栈的数分成两部分
1.比 x 小
2.比 x 大
比x小的数有x-1个,所以这些数的全部出栈方案数为f[x-1]
比x大的数有n-x个,所以这些数的全部出栈方案数为f[n-x]
所以一共有 $f[x-1]*f[n-x]$ 种方案。显而易见,$x$ 取不同值时,产生的出栈序列是相互独立的,所以结果可以累加。$x$的取值范围为 $1$ 至 $ n$,所以结果就为
$f[n] = f[0] * f[n-1] + f[1] * f[n-2] + ... + f[n-1] * f[0]$
**②. 二叉树构成问题**
有n个结点,问总共能构成几种不同的二叉树?
(1)先考虑只有一个节点的情形,设此时的形态有 $f[1]$ 种,那么很明显 $f[1]=1$
(2)如果有两个节点呢?我们很自然想到,应该在 $f[1]$ 的基础上考虑递推关系。 那么,如果固定一个节点后,左右子树的分布情况为$1=1+0=0+1$,故有$f[2] = f[1] + f[1]$
(3)如果有三个节点,我们需要考虑固定两个节点的情况么?(当然不,因为当节点数量大于等于$2$时,无论你如何固定,其形态必然有多种 我们考虑固定一个节点,即根节点)。好的,按照这个思路,还剩2个节点,那么左右子树的分布情况为$2=2+0=1+1=0+2$。 所以有$3$个节点时,递归形式为 $f[3]=f[2]+f[1]*f[1]+f[2]$。(注意这里的乘法,因为左右子树一起组成整棵树,根据排列组合里面的乘法原理即可得出)
(4)那么有n个节点呢?我们固定一个节点,那么左右子树的分布情况为
$n-1=n-1 + 0 = n-2 + 1 = … = 1 + n-2 = 0 + n-1$。此时递归表达式为$f[n] = f[n-1] + f[n-2]f[1] + f[n-3]f[2] + … + f[1]f[n-2] + f[n-1]$
即给定$N$个结点,能构成$h(N)$种不同的二叉树。$h(N)$为卡特兰数的第$N$项。(二叉树性质)
**③、凸多边形的三角形划分**
一个凸的$n$边形,用直线连接他的两个顶点使之分成多个三角形,每条直线不能相交,问一共有多少种划分方案。
这也是非常经典的一道题。我们可以这样来看,选择一个基边,显然这是多边形划分完之后某个三角形的一条边。图中我们假设基边是$p1-pn$,我们就可以用$p1,pn$和另外一个点假设为$pi$做一个三角形,并将多边形分成三部分,除了中间的三角形之外,一边是$i$边形,另一边是$n-i+1$边形。$i$的取值范围是$2$到$n-1$。所以本题的解$c(n)=c(2)c(n-1)+c(3)c(n-2)+...c(n-1)c(2)$。令$t(i)=c(i+2)$。则$t(i)=t(0)t(i-1)+t(1)t(i-2)...+t(i-1)t(0)$。很明显,这就是一个卡特兰数了。
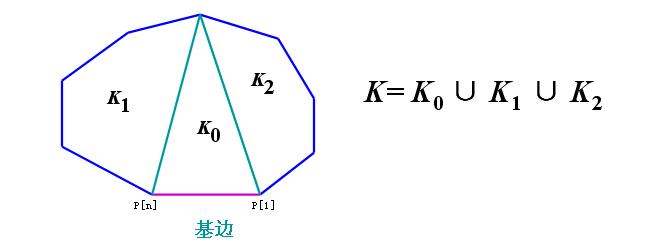
**④、求n+1个叶子的满二叉树的个数**

不证,知道就行
**⑤、路径问题 **
在n*n的格子中,只在下三角行走,每次横或竖走一格,有多少中走法?
其实向右走相当于进栈,向左走相当于出栈,本质就是n个数出栈次序的问题,所以答案就是卡特兰数。(利用这个模型,我们解决这个卡特兰问题的变形问题,并顺便给进出栈问题的解法一个几何解释)
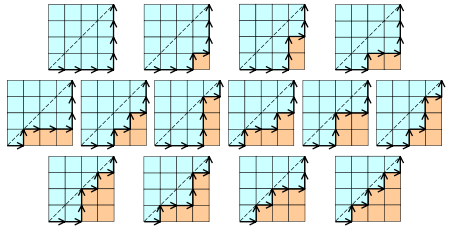
**⑥、划分问题**
将一个凸n+2边形区域分成三角形区域的方法数?
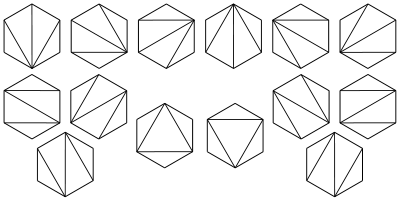
~~证明都差不多啦,自己研究去吧~~
**⑦、握手问题**
2n 个人均匀坐在一个圆桌边上,某个时刻所有人同时与另一个人握手,要求手之间不能交叉,求共有多少种握手方法
##### 4、引理
这就不说了,没啥对考试太实用的,如果实在想看就往上翻,去原博客看,考试知道这些就行了
##### 5、code
说了一堆终于到终点了哈
代码来自 [xiejinhao](https://www.luogu.org/user/196649) (%%%)
①公式1:
```cpp
#include<cstdio>
#define MAX_N 20//这你自己看要定义多大吧
#define ll long long
using namespace std;
int n;
ll f[MAX_N];
int main()
{
f[0]=f[1]=1;
scanf("%d",&n);
for(int i=2;i<=n;i++)
{
for(int j=0;j<i;j++)
{
f[i]+=f[j]*f[i-j-1];
}
}
printf("%lld",f[n]);
return 0;
}
```
②公式2:
```cpp
#include<cstdio>
#define MAX_N 20
#define ll long long
using namespace std;
int n;
ll f[MAX_N];
int main()
{
f[0]=f[1]=1;
scanf("%d",&n);
for(int i=2;i<=n;i++)
{
f[i]+=f[i-1]*(4*i-2)/(i+1);
}
printf("%lld",f[n]);
return 0;
}
```
③公式3:
```cpp
#include<cstdio>
#define MAX_N 20
#define ll long long
using namespace std;
int n;
ll c[MAX_N*2][MAX_N];
int main(){
scanf("%d",&n);
for(int i=1;i<=2*n;i++)
{
c[i][0]=c[i][i]=1;
for(int j=1;j<i;j++)
{
c[i][j]=c[i-1][j]+c[i-1][j-1];
}
}
printf("%lld",c[2*n][n]/(n+1));
return 0;
}
```
④公式4:
```cpp
#include<cstdio>
#define MAX_N 20
#define ll long long
using namespace std;
int n;
ll c[MAX_N*2][MAX_N];
int main(){
scanf("%d",&n);
for(int i=1;i<=2*n;i++)
{
c[i][0]=c[i][i]=1;
for(int j=1;j<i;j++)
{
c[i][j]=c[i-1][j]+c[i-1][j-1];
}
}
printf("%lld",c[2*n][n]-c[2*n][n-1]);
return 0;
}
```
~~不懂看公式去~~
卡姿兰数完结
#### 2、排列组合
##### 1、计数原理:
如果 A 地到 B 地有三条路径,B 地到 C 地有两条路径,那么A 到 C 共有 2 * 3 = 6 种方案
如果 A 还有一种直接到 C 的方案,那么就一共有 7 种方案
上面就是加法原理和乘法原理(不知道自行[百度](https://baike.baidu.com/item/%E8%AE%A1%E6%95%B0%E5%8E%9F%E7%90%86/4032370?fr=aladdin),~~好像不知道也无所谓哦~~)
##### 2、排列和组合:
从 n 个元素中取出 m 个元素,排成一排,叫做从 n 个元素中取出 m 个元素的一个排列
$$
A_{n}^{m}=\frac{n!}{(n-m)!}
$$
从 n 个元素中取出 m 个元素的所有组合(不管其顺序)的个数,叫做 n 个元素中取出 m 个元素的组合数
$$
C_{n}^{m}=\frac{n!}{m!(n-m)!}
$$
这东西太多了,我们讲几个基础的
$$
C_{n}^{m}=C_{n}^{n-m},C_{n}^{0}=C_{n}^{n}=1
$$
可以理解为:将原本的每个组合都反转,把原来没选的选上,原来选了的去掉,这样就变成从n个元素种取出n−m个元素,显然方案数是相等的。
$$
C_{n}^{m}=C_{n-1}^{m}+C_{n-1}^{m-1}
$$
可理解为:含特定元素的组合有$C^{m-1}_{n-1}$,不含特定元素的排列为$C^{m}_{n-1}$
组合数求和公式:
$$
C_{n}^{0}+C_{n}^{1}+C_{n}^{2}+...+C_{n}^{n}=2^{n}
$$
~~自己记去~~
#### 3、二项式定理
可以将x+y的任意次幂展开成和的形式
$$
(x+y)^{n}=\binom{n}{0}x^{n}y^{0}+\binom{n}{1}x^{n-1}y^{1}+\binom{n}{2}x^{n-2}y^{2}+...+\binom{n}{n-1}x^{1}y^{n-1}+\binom{n}{n}x^{0}y^{n}
$$
其中每个$\binom{n}{k}$为一个称作二项式系数的特定正整数,其等于$\frac{n!}{k!(n-k)!}$。这个公式也称二项式公式或二项恒等式。使用求和符号,可以把它写作
$$
(x+y)^{n}=\sum_{k=0}^{n}\binom{n}{k}x^{n-k}y^{k}=\sum_{k=0}^{n}\binom{n}{k}x^{k}y^{n-k}
$$
[P1313 计算系数](https://www.luogu.org/problem/P1313)
#### 4、杨辉三角
来自古人的神秘力量
[大佬博客](https://www.cnblogs.com/1024th/p/10623541.html)的搬运工——ollie

杨辉三角可以帮助你更好地理解和记忆组合数的性质:
1. 第$n$行的$m$个数可表示为 $C^{m-1}_{n-1}$,即为从$n-1$个不同元素中取$m-1$个元素的组合数。
2. 第$n$行的数字有$n$项。
3. 每行数字左右对称(第$n$行的第$m$个数和第$n-m+1$个数相等,$C_{n}^{m}=C_{n}^{n-m}$,由$1$开始逐渐变大。
4. 每个数等于它上方两数之和(第$n+1$行的第$i$个数等于第$n$行的第$i-1$个数和第$i$个数之和,即$C_{n+1}^{i}=C^{i}_{n}+C_{n}^{i-1}$。
1. $(a+b)^{n}$的展开式中的各项系数依次对应杨辉三角的第$n+1$行中的每一项(二项式定理)。
**code:**
```cpp
c[1][1] = 1;
for(int i = 2; i <= n; i++)
for(int j = 1; j <= i; j++)
{
c[i][j] = c[i-1][j] + c[i-1][j-1];
}
```
[P1118 数字三角形](https://www.luogu.org/problem/P1118)
[P2822 组合数问题](https://www.luogu.org/problem/P2822)
#### 5、Fibonacci数列
都知道吧,什么是Fibonacci数列。
递推式:
$$
F(1)=1,F[0]=0
$$
$$
F(n)=F(n-1)+F(n-2)
$$
通项公式:
$$
F(n)=\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{n}-(\frac{1-\sqrt{5}}{2})^{n}]
$$
关于斐波那契的一些恒等式:
1:$F(1)+F(2)+F(3)+...+F(n)=F(2n-1)$
2:$F(1)^{2}+F(2)^{2}+F(3)^{2}+...+F(n)^{2}=F(n)F(n+1)$
3:$F(1)+F(3)+F(5)+...+F(2n-1)=F(2n)$
4:$F(2)+F(4)+F(6)+...+F(2n)=F(2n+1)-1$
5:$F(n)=F(m)F(n-m+1)+F(m-1)F(n-m)$ $ps:n>m$
6:$F(n-1)F(n+1)=F(n)^{2}+(-1)^{n}$
**斐波那契的数论相关:**
**性质1**:$gcd(F(n),F(m))=F(gcd(n,m))$
反证法:假设不互素。那么有$a=gcd(F(n),F(n-1)),a>1$.
那么对于$F(n)=F(n-1)+F(n-2)$.因为$a|F(n),a|F(n-1)$,所以$a|F(n-2)$.
由于$a|F(n-1),a|F(n-2)$.又可以获得$a|F(n-3)$...可以知道$a|F(1)$其中。$F(1)=1$.
如果$a|F(1)->a|1$那么与$a>1$不符。相邻互素得证.(其实 $a|F(2)$就已经不行了.)
**性质2:** $n|m\Leftrightarrow F(n)|F(m)$
证明:当$n|m$时,
$$
gcd(F(n),F(m))=F(gcd(n,m))=F(n)\Rightarrow F(n)|F(m)
$$
[P1306 斐波那契公约数](https://www.luogu.org/problem/P1306)
### 九、数学期望
所有的权值乘以它对应的概率
通俗一点就是设$X[i]$为$i$的权值,$P[i]$是$i$对应出现的概率,期望值为$f$,有:
$$
f=\sum_{i=1}^{n}X[i]* P[i]
$$
## 完结撒花
### 还有部分内容未补上,后期补充上去