人伦之光 Splay
Splay
一种平衡树, 虽然常数较大, 但是凭着特殊的功能和较小的代码难度成为了很多人初学平衡树的首选. (当然我是受李煜东的 进阶指南 影响从 Treap 学起的)
Binary Search Tree (二分查找树)
想象一种二叉树, 它可以用来维护一个集合, 可以用来查找, 删除和添加元素, 还支持查找集合的最值 (权值最大/小的元素) ,一个节点的前驱/后缀 (权值严格小/大于这个元素的权值最大/小的元素). 这就是二分查找树, 简称 BST.
这种树满足父亲节点权值大于的左子树中任意节点的权值, 小于右子树所有节点的权值.
查找一个元素时, 从根节点开始, 向下一步步递归查找, 如果查找的权值比当前节点大, 就查找它的右儿子; 如果查找的权值比当前节点小, 就查找它的左儿子; 如果当前节点的权值就是要查找的权值, 就不用找了, 说明已经找到了.
如果找到最后, 最后经过的节点不是要找的节点, 却没有对应的左/右子树, 说明不存在相应元素.
添加元素也是相似的, 先查找这个权值, 如果找到了, 更新对应节点的计数器即可; 如果找不到, 就给最后一个经过的节点添加一个儿子, 左右取决于插入的权值和该节点权值的关系.
删除, 查找最值, 查找前驱/后缀等操作也是差不多的思想, 无非是根据需要的权值在 BST 找到对应位置, 在这个位置上进行操作罢了, 所以都离不开查找这个步骤.
因为基于查找, 每种操作, 除查找之外的部分复杂度都是
平衡树
由定义可以得出一个 BST 的性质, 对于同一组元素, BST 不唯一. 对于任何集合, 对应的 BST 的深度在构造合理的前提下都能达到
深度要达到
这样构造的 BST 称作平衡树. 而 Splay 就是一种能使 BST 趋近于平衡的构造和维护方式 (或者说操作), 这样维护的 BST 一般称为 Splay 树, 简称 Splay.
旋转
一种对 BST 进行局部操作但是不会破坏 BST 性质的操作, 是 Splay 等基于旋转的平衡树的基础.
前排提醒: 由于旋转存在父亲要变成儿子的儿子等神奇操作, 可能引发伦理危机. 好在幸亏节点不讲伦理, 所以学习这部分内容时请放下你的道德. 但是一定不要用你身边的朋或家人进行类比, 否则后果自负.
对于一个节点
由 BST 性质得
由于旋转的参照物不同, 会对旋转结果产生不同的影响, 所以针对参考系进行分类讨论. (当然有很多自创的名词, 但是为了更好表达这种思想, 这也是必要的)
规定下面介绍的旋转规则中所有公式表达中的节点 (如
绕自旋转
绕自旋转又分为两个方向: 左旋 (Zag) 和右旋 (Zig).
-
Zag (左旋)
旋转
i 的意义是使RS_i 变成i 的父亲. 这时如果要维护 BST 的性质,i 只能做RS_i 的左儿子. 而旋转后RS_i ,i 和他们的子树上的节点的权值与Val_{Fa_i} 的大小关系不变, 所以旋转前i 是Fa_i 的哪边的儿子, 旋转后RS_i 就是Fa_i 的哪边的儿子.如果想象着这种操作的动态过程, 可以发现操作相当于 $LS_{RS_i}$ 和 $RS_i$ 绕 $i$ 逆时针旋转, 然后重新连边. 在屏幕前的视角就是向左旋转, 故名 `左旋` 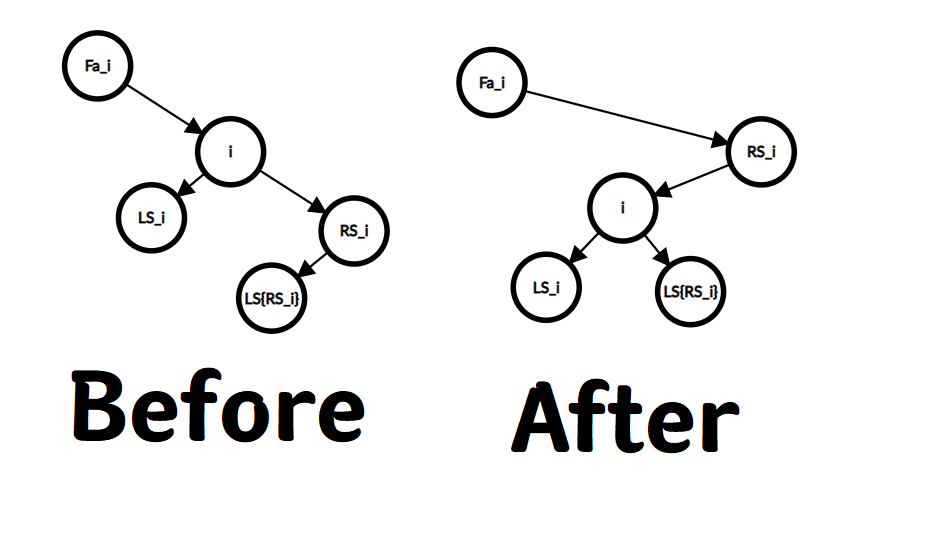 -
Zig (右旋)
参考结构化学中的手性的概念, Zig 就是 Zag 的对映操作. 也就是以
Fa_i - i 中轴线为对称轴, 和 Zig 对称的操作, 对细节不再赘述.
绕父旋转
在这种规则下, 旋转
这时
同理,
由于绕父旋转的方式在一个特定位置的节点上是一定的, 所以没有绕自旋转的 Zig, Zag 规则之分. 其本质就是根据不同相对位置关系对父亲进行 Zig/Zag 的调用, 所以是绕
伸展 (Splay)
由上面的旋转规则可以发现, 如果针对一个点一直绕父旋转, 每次这个点的深度都减少
再引入一个定义: 性别 (虽然不是官方叫法, 但我决得很形象, 姑且先这样叫). 设一个点的左儿子是男性, 右儿子是女性.
规定一种旋转准则:
-
如果还有爷爷
- 如果父子同性
则绕爷旋转. 这时原来的爷爷成了兄弟.
- 如果父子异性 (有些奇怪, 那就将父子理解成辈分好了)
则绕父旋转. 原来的爷爷成了父亲, 原来的父亲成了儿子. 原父亲性别不变, 和当前节点同性.
-
如果没有爷爷
则绕父旋转. 这是操作的边界, 这次旋转完后, 这个节点就成为了树根, 连父亲都没有了.
我们把根据这种准则将点 Splay(i).
定义一个操作经过的最后一个还在集合中的节点是目标节点. (这里强调还在集合中是因为删除一个节点后, 被删除的节点最后经过, 而显然这个点已经不在了)
通过 Splay 操作优化 BST 深度的操作比较玄学, 证明也更加麻烦, 所以直接给出具体操作: (证明困难户直接放弃)
每次进行操作后, Splay 目标节点. 就能使过程中 Splay 树的深度维持在近似
但是对于删除操作略有不同, 这时可以将一般操作和 Splay 的操作交换一下顺序. 具体操作是先将待删除点 Splay 到树根, 删除. 剩下两棵子树, 记为
操作详解 (附代码)
众所周知, 一般的数据结构都是由结构体和函数构成的, 所以接下来将一个一个函数去解析.
Rotate()
先写最底层的旋转, 因为 Splay 用到的就只有绕父旋转, 所以这里就只写绕父旋转, 不单独写 Zig, Zag 了.
旋转的同时维护子树大小
Rotate() 的细节非常多, 大部分都在注释中给出.
inline void Rotate(register Node *x) { // 绕父旋转
if (x->Fa){
Node *Father(x->Fa); // 暂存父亲
x->Fa = Father->Fa; // 父亲连到爷爷上
if(Father->Fa) { // Grandfather's Son (更新爷爷的儿子指针)
if(Father == Father->Fa->LS) { // Left Son
Father->Fa->LS = x;
}
else { // Right Son
Father->Fa->RS = x;
}
}
x->Size = x->Count; // x 的 Size 的一部分 (x->Size = x->LS->Size + x->RS->Size + x->Count)
if(x == Father->LS) { // x is the Left Son, Zag(x->Fa)
if(x->LS) {
x->Size += x->LS->Size;
}
Father->LS = x->RS, x->RS = Father;
if(Father->LS) {
Father->LS->Fa = Father;
}
}
else { // x is the Right Son, Zig(x->Fa)
if(x->RS) {
x->Size += x->RS->Size;
}
Father->RS = x->LS, x->LS = Father;
if(Father->RS) {
Father->RS->Fa = Father;
}
}
Father->Fa = x/*父亲的新父亲是 x*/, Father->Size = Father->Count/*Father->Size 的一部分*/;
if(Father->LS) { // 处理 Father 两个儿子对 Father->Size 的贡献
Father->Size += Father->LS->Size;
}
if(Father->RS) {
Father->Size += Father->RS->Size;
}
x->Size += Father->Size; // Father->Size 更新后才能更新 x->Size
}
return;
} Splay()
由于已经封装了 Rotate(), 加上逻辑比较简单, 所以 Splay() 也会更规整简洁好看一些.
因为任何操作的寻址都是从根开始的, 所以每次 Splay 也要实时更新根的位置, 记录在指针
void Splay(Node *x) {
if(x->Fa) {
while (x->Fa->Fa) {
if(x == x->Fa->LS) { // Boy
if(x->Fa == x->Fa->Fa->LS) { // Boy & Father
Rotate(x->Fa);
}
else { // Boy & Mother
Rotate(x);
}
}
else { // Girl
if(x->Fa == x->Fa->Fa->LS) { // Girl & Father
Rotate(x);
}
else { // Girl & Mother
Rotate(x->Fa);
}
}
}
Rotate(x);
}
Root = x;
return;
}Insert()
插入的大体框架是先寻址, 再操作, 最后 Splay.
寻址可以递归实现, 优点是思路清晰, 适合对算法仍不熟悉的人; 但是循环实现的常数小, 代码难度相对较低, 适合熟练者和考场代码.
void Insert(register Node *x, unsigned &y) {
while (x->Value ^ y) {
++(x->Size); // 作为加入元素的父节点, 子树大小增加
if(y < x->Value) {// 在左子树上
if(x->LS) { // 有左子树, 往下走
x = x->LS;
continue;
}
else { // 无左子树, 建新节点
x->LS = ++CntN;
CntN->Fa = x;
CntN->Value = y;
CntN->Size = 1;
CntN->Count = 1;
return Splay(CntN);
}
}
else { // 右子树的情况同理
if(x->RS) {
x = x->RS;
}
else {
x->RS = ++CntN;
CntN->Fa = x;
CntN->Value = y;
CntN->Size = 1;
CntN->Count = 1;
return Splay(CntN);
}
}
}
++(x->Count), ++x->Size; // 原来就有对应节点
Splay(x); // Splay 维护 BST 的深度复杂度
return;
}Delete()
应该是最复杂的一个操作了, 需要不止一次 Splay.
过程仍然是先寻址, 如果找到对应的节点就 Splay 到根上, 根据
-
Count > 1 无需删点, 只要修改
Size 和Count 即可, 由于当前节点已经是根了, 所以它的Count 修改不影响其它点的Size . -
Count = 1 这时需要将该点删除, 这时当前节点
x 是根节点, 删除x 后有几种情况要讨论, 剩下两棵子树, 剩下左子树, 剩下右子树. (不能一棵都不剩, 原因会在后面讲哨兵的部分解释).- 剩一棵子树
这棵子树便是新的 BST, 直接将这个子树根的父亲指针置空, 然后将
Root 指针指向这个子树根.- 剩两棵子树
随便挑选一棵 (这里选左子树) 为根, 将左儿子的父亲指针置空, Splay 左子树中的最大值作为 BST 新根, 右儿子就是原来根的右儿子.
代码有 Rotate() 的特点, 指针连接非常多, 每一步的意义都明白后, 整体理解就没那么难了.
void Delete(register Node *x, unsigned &y) {
while (x->Value ^ y) {
x = (y < x->Value) ? x->LS : x->RS;
if(!x) {
return;
}
}
Splay(x);
if(x->Count ^ 1) { // Don't Need to Delete the Node
--(x->Count), --(x->Size);
return;
}
if(x->LS && x->RS) { // Both Sons left
register Node *Son(x->LS);
while (Son->RS) {
Son = Son->RS;
}
x->LS->Fa = NULL/*Delete x*/, Splay(Son);// Let the biggest Node in (x->LS) (the subtree) be the new root
Root->RS = x->RS;
x->RS->Fa = Root; // The right son is still the right son
Root->Size = Root->Count + x->RS->Size;
if(Root->LS) {
Root->Size += Root->LS->Size;
}
return;
}
if(x->LS) { // x is The Biggest Number
x->LS->Fa = NULL; // x->LS is the new Root
Root = x->LS;
}
if(x->RS) { //x is The Smallest Number
x->RS->Fa = NULL; // x->LS is the new Root
Root = x->RS;
}
return;
}Value_Rank()
根据权值查排名, 可能会没有对应的权值出现. 规定排名为比权值这个数小的元素数量.
寻址过程中统计权值较小的元素数量, 由每个节点的经过方式决定. 如果往左子树走, 无需统计; 如果往右子树走, 统计左子树
-
y \leq x \rightarrow LS \rightarrow Size 要找的点在左子树, 直接前往左子树, 继续寻找.
-
y > x \rightarrow LS \rightarrow Size 要找的点不在左子树, 去掉左子树后排
y - x \rightarrow LS \rightarrow Size 名. 将y 减去x \rightarrow LS \rightarrow Size 后, 再次分两种情况讨论:(后面的y 是减去x \rightarrow LS \rightarrow Size 后的)-
y \leq x \rightarrow Count
这时要找的元素就是
x , 直接Splay(x) , 将答案存到根上.-
y > x \rightarrow Count
要找的元素在右子树. 在右子树中的名次是
y - x \rightarrow Count . -
这时操作中唯一一个不按权值寻址的操作, 但是结构也不复杂, 很清晰的过程.
void Rank_Value(register Node *x, unsigned &y) {
while (x) {
if(x->LS) {
if(x->LS->Size < y) {//Not in the Left
y -= x->LS->Size;
}
else { // In Left Subtree
x = x->LS;
continue;
}
}
if(y > x->Count) { // In Right Subtree
y -= x->Count;
x = x->RS;
continue;
}
return Splay(x); // Just Look for x
}
}Before()
相当于 <set> 中的 lower_bound(), 求集合中权值严格小于
仍然是寻址, 由于要求严格小于, 所以对于
这个操作的分类讨论比较多
-
y \leq x \rightarrow Value 往左走, 根据左儿子情况再次分类
- 有左子树
走左子树
- 无左子树
本来要找比
x 小的元素, 可是在x 的子树上已经不存在了, 所以只能在x 的祖先上找. 因为x 的深度最大的小于y 的祖先x' 一定是往右边走的. 然后接下来的每一步都往左走, 所以x 是x' \rightarrow RS 的子树上最小的元素. 由 BST 的性质得,x' \rightarrow Value 和它右子树上的最小值x \rightarrow Value 中间没有其它元素. 又因为x \rightarrow Value \geq y > x' \rightarrow Value , 所以x' 就是要找的元素.所以做法是: 从
x 往上跳, 跳到祖先x' (满足x' \rightarrow Value < y ) 为止, Splay(x'), 返回, 树根即为所求. -
y > x \rightarrow Value - 有右子树
走右子树
- 无右子树
说明
x 就是要找的点,Splay(x) , 返回, 答案就是根. 证明方式差不多,x 一定是它的子树中最大的, 对于x 的深度最大的大于等于y 的祖先x' , 一定是左转到x' \rightarrow LS , 然后一连串右转到x , 说明x 是x' \rightarrow LS 的子树中最大的节点, 同理, 有x 是小于x' 的最大元素. 又因为x \rightarrow Value < y \leq x' \rightarrow Value , 所以Splay(x) , 返回, 根即为所求.
代码比文字更易懂, 分为三个方向, 左转, 右转和上转, 两种边界, 上边界 (往祖先跳而找到的答案) 和右边界 (往右子树走不通而达到的边界).
void Before(register Node *x, unsigned &y) {
while (x) {
if(y <= x->Value) { // Go left
if(x->LS) {
x = x->LS;
continue;
}
while (x) { // Go Up
if(x->Value < y) {
return Splay(x);
}
x = x->Fa;
}
}
else { // Go right
if(x->RS) {
x = x->RS;
continue;
}
return Splay(x); // Value[x] < Key
}
}
}After()
相当于 <set> 中的反向 lower_bound(), 是 Before() 的对应操作, 反过来理解就好了.
void After(register Node *x, unsigned &y) {
while (x) {
if(y >= x->Value) { // Go right
if(x->RS) {
x = x->RS;
continue;
}
while (x) { // Go Up
if(x->Value > y) {
return Splay(x);
}
x = x->Fa;
}
}
else { // Go left
if(x->LS) {
x = x->LS;
continue;
}
return Splay(x);
}
}
}Build()
由于 Splay 树的常数非常大, 所以在初始化一个集合时, 一个一个 Insert 会非常不划算, 所以可以写一个初始化的程序, 快速建好这棵树.
提前预处理两个数组,
void Value_Rank(register Node *x, unsigned &y, unsigned &Rank) {
while (x->Value ^ y) { // Go Down
if(y < x->Value) { // Go Left
if(x->LS) {
x = x->LS;
continue;
}
return; // No more numbers smaller than y, Rank is the rank
}
else { // Go Right
if(x->LS) {
Rank += x->LS->Size; // The Left Subtree numbers
}
Rank += x->Count; // Mid Point numbers
if(x->RS) {
x = x->RS;
continue;
}
return; // No more numbers bigger than y, Rank is the rank
}
}
if(x->LS) { // now, x->Value == y
Rank += x->LS->Size;
}
return;
}哨兵
因为每次操作需要从根开始, 所以空 BST 是不能进行任何操作的, 但是应用中却可能出现空的集合, 这时必须要存在一个节点, 它既存在, 又不存在. 存在的意义是在 BST 中确实有这个节点, 可以在维护的集合为空时作为根节点; 不存在的意义是它在维护的集合中不存在, 任何查询操作都不会被它影响, 删除和插入也和这个节点没有关系.
这个节点必须满足它的
所以解决方案是在 Build() 前, 在待建树的集合数组末尾加入一个值域之外的最大值
例题: 普通平衡树 (数据加强版)
题意: 维护一个给定的数集, 支持六种操作, 这六种操作便是前面分析的 Splay 树支持的那六种操作
-
Insert
-
Delete
-
Value_Rank
-
Rank_Value
-
Before
-
After
强制在线, 本次操作值 = 上个答案 ^ 本次输入值.
输出所有答案异或和.
在普通平衡树的基础上, 写一个处理集合, 回答询问的接口即可.
下面的代码省略了前面列举的函数, 即 Splay 树对于本题的接口.
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <ctime>
#include <iostream>
#include <map>
#include <queue>
#include <vector>
#define Wild_Donkey 0
using namespace std;
inline unsigned RD() { // Fast Read
unsigned intmp = 0;
char rdch(getchar());
while (rdch < '0' || rdch > '9') {
rdch = getchar();
}
while (rdch >= '0' && rdch <= '9') {
intmp = intmp * 10 + rdch - '0';
rdch = getchar();
}
return intmp;
}
unsigned a[100005], b[100005], m, n, RealN(0), Cnt(0), C, D, t, Tmp(0);
bool Flg(0);
struct Node {
Node *Fa, *LS, *RS;
unsigned Value, Size, Count;
}N[1100005], *CntN(N), *Root(N);
signed main() {
register unsigned Ans(0); // 记录
n = RD();
m = RD();
a[0] = 0x7f3f3f3f;
for (register unsigned i(1); i <= n; ++i) { // 原集合
a[i] = RD();
}
sort(a + 1, a + n + 1); // 排序
for (register unsigned i(1); i <= n; ++i) { // 去重
if(a[i] ^ a[i - 1]) { // A new number
b[++RealN] = 1;
a[RealN] = a[i];
}
else { // Old number
++b[RealN];
}
}
a[++RealN] = 0x7f3f3f3f; // 加入哨兵
b[RealN] = 1;
Build(1, RealN, NULL); // 建树
Root = N + 1; // 初始化根 (根是第一个点, 因为递归建树是 DFS, 根是 DFS 序最小的)
for (register unsigned i(1), A, B, Last(0); i <= m; ++i) {
A = RD();
B = RD() ^ Last; // 强制在线, 处理操作值
switch(A) { // 分别是对应的 6 个操作
case 1:{
Insert(Root, B);
break;
}
case 2:{
Delete(Root, B);
break;
}
case 3:{
Last = 1; // 初始化 Last, 答案直接累计在传入的 Last 中
Value_Rank(Root, B, Last);
Ans ^= Last;
break;
}
case 4:{
Rank_Value(Root, B);
Last = Root->Value; // 4, 5, 6 操作的答案都存在树根上, 作为根节点的权值存在
Ans ^= Last;
break;
}
case 5:{
Before(Root, B);
Last = Root->Value;
Ans ^= Last;
break;
}
case 6:{
After(Root, B);
Last = Root->Value;
Ans ^= Last;
break;
}
}
}
printf("%u\n", Ans);// 输出异或和
return Wild_Donkey;
}小结
Splay 虽然不是我学习的第一种平衡树, 但是却是我 AC 的第一棵平衡树 Dec.1st 2020, 当时感觉自己都明白了, 结果如今 Apr.29th 2021 还是调了几天. 果然, 算法这种东西, 不练习是记不住的, 接下来要加强练习.
但是对于一个算法, 巩固它的更好方法貌似是以这个算法为前置知识去学习知识树上的后继节点. 所以, LCT, 我来了.
最后: 话说我现在一篇博客字符数量 15k+ 已经变成常态了吗? 还记得 10k 字符的后缀自动机 已经让当时的我震惊了, 随之而来的 SA-IS 的 16k 字符更是让我刷新了对自己码字能力的评估, 这次更是直接干到了 17.5k. 果然学 OI 是能提升语文水平的 (貌似还有英语水平).