直线和圆习题(目前持续更新)
BrotherCall
·
·
个人记录
1. 若过点 P(1,0),Q(2,0),R(4,0),S(8,0)作四条直线构成一个正方形,则该正方形的面积可能等于 \color{red}ABD
A.\frac{16}{17}/B.\frac{36}{5}/C.\frac{26}{5}/D.\frac{196}{53}
这里我们设过点 X 的直线为 x 。
①:p 与 q 平行,r 与 s 平行 --> $3\sin \theta = 6\cos \theta$ --> $\tan \theta = 2$ ,$S = \frac{16}{17}
②:p 与 r 平行,q 与 s 平行 --> 4\cos \theta = \sin \theta --> \tan \theta = 4 , S = \frac{36}{5}
③:p 与 s 平行,q 与 r 平行 --> 7\sin \theta = 2\cos \theta --> \tan \theta = \frac{2}{7},S = \frac{196}{53}
2. 1949年公布的《国旗制法说明》中就五星的位置规定:大五角星有一个角尖正向上方,四颗小五角星均各有一个角尖正对大五角星的中心点。有人发现,第三颗小星的姿态与大星相近。为便于研究,如图,以大星的中心点为原点,建立直角坐标系,OO_1,OO_2,OO_3,OO_4 分别是大星中心点与四颗小星中心点的连线,\alpha = 16 \degree,则第三颗小星的一条边AB所在直线的倾斜角约为 \color{red}2 \degree
---
### 3. 已知 $A(-1 , 3) , B(2 , -1)$ 两点到直线 $l$ 的距离分别为 2 和 3,则满足条件的直线 $l$ 共有 $\color{red}3$ 条
$\color{red}solution:$ 这题思路是很巧妙的,我一开始没想到。
要找到两定点距离为定值的线,首先考虑找点。
$|AB| = 5$ ,我们以 $A$ 为圆心 $2$ 为半径画圆,再以 $B$ 为圆心 $3$ 为半径画圆,发现正好外切。
然后满足题意直线条数其实就是公切线条数,这应该算一个结论吧,技巧性挺强。
---
### 4. 将函数 $y = \sqrt{13 - x^2} - 2 (x ∈ [-3,3])$ 的图像绕点 $(-3 , 0) $ 逆时针旋转 $\alpha(0 \leqslant \alpha \leqslant \theta)$,得到曲线 $C$ ,对于每一个旋转角 $\alpha$,曲线 $C$ 都是一个函数的图像,则 $\tan \theta = \color{red}\frac{2}{3}
介绍下题解解法:临界情况就是把圆心和左端点连线拽成平的,也就是说新圆心在 $x$ 轴上,于是 $\theta$ 就等于原圆心和 $x$ 轴的夹角。结束了,很巧妙,但我想不到。
---
### 5. 若倾斜角为锐角的直线 $L:y=kx+\sqrt{2}+1$ 与圆 $C:x^{2}+y^{2}-2x-2y-2=0$ 交于 $A$ 、$B$ 两点,当三角形$ABC$的面积最大时,直线 $L$ 的斜率为 $\color{red}2\sqrt2
然后令圆心到直线距离为 $\sqrt2$ 即可解出答案。
---
### 6. 设直线 $3x+4y-5 = 0$ 与圆 $C_1$ : 交于 $A, B$ 两点, 若圆 $C_2$ 的圆心在线段 $AB$ 上, 且圆 $C_2$ 与圆 $C_1$ 相切, 切点在圆 $C_1$ 的劣弧上, 则圆 $C_2$ 的半径的最大值是 $\color{red}2
感谢 syk 提供的思路 /bx 。
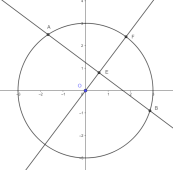
如图即可求出答案。圆心是 $(\frac{3}{5} , \frac{4}{5})$,圆上一点是 $(\frac{9}{5} , \frac{12}{5})$ ,半径计算得为 2 。
---
### 7. 过原点 O 作直线 $l:(2m+n)x+(m-n)y-2m+2n=0$ 的垂线,垂足为 P ,则 P 到直线 $x-y+3=0$ 的距离的最大值为 $\color{red}\sqrt2+1
第一个式子化成 $m(2x+y-2) + n(x-y+2)=0$,可得到该直线恒过点 $(0,2)$。
这个垂线,总让人感觉要设个斜率之积为 $-1$ 的直线。
实际上最好的做法是:这个垂足在以 $(0,0)$ 和 $(0,2)$ 为直径的圆上。
然后题目转化为定直线到圆上一点距离最大值。
---
### 8. 从圆 $C_1:x^2+y^2=4$ 上的一点向圆 $C_2:x^2+y^2=1$ 引两条切线,连接两切线间的线段称为切点弦,则圆 $C_2$ 内不与任何切点弦相交的区域面积为 $\color{red}\frac{\pi}{4}
要说用什么严谨方法,我偏向于直接套切点弦公式,然后不难发现圆心到动直线的距离是个定值。