树形 DP 学习笔记(二)
前言
本文讲解如何用树形 DP 解决兄弟节点间有数量上的约束关系的问题。解决方法大致是转化为多重背包问题,把一个节点的子节点视为物品,讲题目给定的数量约束视为背包容量。
upd.24/11/16 来填坑了。
写一道题目了解一下大致框架。
P2015 二叉苹果树
设
对于根节点 dp[cur][j]=max(dp[cur][j],dp[cur][j-k-1]+dp[nxt][k]+w);。需要注意的是,方程中的 dp[cur][j-k-1] 并不是在
至此,这道题已经有了正解,但是我们还可以进一步优化。
我们
因为作者个人能力有限,请读者移步别处查看此结论的证明。
贴个代码罢。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=105;
int n,q;
int siz[N];
int dp[N][N];
struct node{
int id,val;
};
vector<node>v[N];
void DFS(int x,int fa){
siz[x]=0;
for(int i=0;i<v[x].size();i++){
int to=v[x][i].id,w=v[x][i].val;
if(to==fa)
continue;
DFS(to,x);
siz[x]+=siz[to]+1;
for(int j=min(siz[x],q);j>=0;j--)
for(int k=0;k<=min(siz[to],j-1);k++)
dp[x][j]=max(dp[x][j],dp[x][j-k-1]+dp[to][k]+w);
}
return;
}
signed main(){
cin>>n>>q;
for(int i=1;i<n;i++){
int x,y,z;
cin>>x>>y>>z;
v[x].push_back({y,z});
v[y].push_back({x,z});
}
DFS(1,0);
cout<<dp[1][q];
return 0;
}P2014 [CTSC1997] 选课
和前一道例题大同小异。
根据选课的约束关系建树。然后设
故最后答案为
P1272 重建道路
上点难度。
状态比较好设:v[i].size()。
转移呢?先放个代码:dp[cur][j]=min(dp[cur][j],dp[nxt][k]+dp[cur][j-k]-1);
这个转移唯一难以理解的是,这个 -1 是怎么回事?其实很简单,别忘了,dp[cur][j-k] 统计的是
这题的答案也有点小坑。应该这么统计:
int ans=dp[1][p];
for(int i=2;i<=n;i++)
ans=min(ans,dp[i][p]+1);为什么呢?当我们选点 dp[i][p] 只是求取的将其子树中某些边删去的答案,但它到其父亲的边也要删去,才能将他这棵子树“剔除”在外。故删边数加
POJ1848 Tree
前言:恶心题目,甚至没提到有多测,而且 POJ 不支持看数据点,导致我现在没有条出来。不过 no problem。同时其实应该放到学习笔记(一)中的因为不是树上背包。不过思维难度较大,就放(二)里了。
题意:给定一棵树,求最少要加多少条边使得树上每个节点都仅在一个简单环里。
设状态
然后对于边
-
-
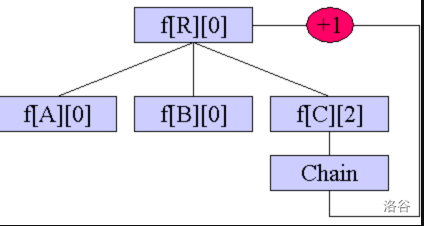 表示 $u$ 从 $v$ 伸出去的链上接回来,加了一条边。 -
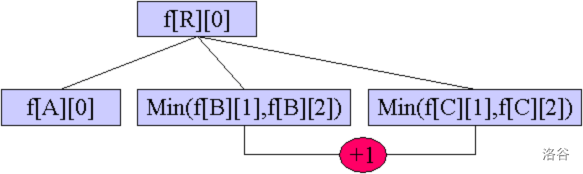 表示 $R$、$B$ 延伸部分、$C$ 延伸部分组成环。注意此时 $B,C$ 不能已全部成环,这样无法连接,所以不将 $F[B][0],F[C][0]$ 计入贡献。 -
什么?代码?没有。
P8867 [NOIP2022] 建造军营
同样不是树形背包但是难度比较大,故放至(二)。本文同步载于我的另一篇文章,部分参考本题题解区第一篇题解。
首先缩点,将整张图转化为一棵树。那么树上一个节点代表一个边双,每一个边双里的点和边都可以自由分配。(敌人无论如何都无法炸一条边使得这个边双不连通。)
转化为树之后,问题成为一个显然的树形 DP。设计状态为
这个限制第一篇题解中没有做详细解释,我自己的理解是:这样做可以不重不漏且方便统计。需要注意的一点是这样做不会漏掉某子树内的军营自成一体,不通过已派兵看守的边与
同时还要有一个限制:强制限制不选
那么有了这两个限制,转移就变得简单而不重不漏了。首先赋初值:
然后进行转移:
- 计算
dp_{x,0} :比较简单,dp_{x,0}\leftarrow dp_{x,0}\times \prod_{to\in son(x)}(2\times dp_{to,0}) ,表示乘上各个儿子子树方案数的乘积。单棵子树的方案数为dp_{to,0}\times 2 ,其中2 表示边to\to x 选或不选都可以。 -
计算
dp_{x,1} :考虑一棵一棵添加子树。- 若到新增前当前子树
x 内未建造过军营,那么当前儿子to 子树内必须有军营,即dp_{x,1}\leftarrow dp_{x,1}+dp_{x,0}\times dp_{to,1} 。 - 若到新增前当前子树
x 内已有军营,那么当前儿子子树内可以有军营也可以没有,即dp_{x,1}\leftarrow dp_{x,1}+dp_{x,1}\times(dp_{v,1}+2\times dp_{v,0}) ,2 的含义同上文。
综上,即
dp_{x,1}\leftarrow dp_{x,1}+dp_{x,0}\times dp_{to,1}+dp_{x,1}\times(dp_{v,1}+2\times dp_{v,0}) 。 - 若到新增前当前子树
最后是统计答案。令
那么题目就做完了,笔者有一个小错误一直卡在 15pts,直到 2025.5.3 终于调出来了。再次纪念并放上代码。代码不难但细节很多,码量较大:
#include<bits/stdc++.h>
#define int long long
#define ID(i) i*2-2
using namespace std;
const int N=5e5+5,M=1e6+5,mod=1e9+7;
int n,m,tot,col,ans,dfn[N],low[N],is[M<<1],vis[N],dccV[N],dccE[N],in[N],siz[N],dp[N][2];
struct node{int to,id;};
struct edge{int x,y;}e[M];
vector<node>v[N];
vector<int>g[N];
int fpow(int a,int b,int p){int ans=1;while(b){if(b&1)ans=ans*a%p;a=a*a%p,b/=2;}return ans;}
void Tarjan(int x,int preid){
dfn[x]=low[x]=++tot;
for(int i=0;i<v[x].size();i++){
int to=v[x][i].to,id=v[x][i].id;
if((id^1)==preid)continue;
if(!dfn[to]){
Tarjan(to,id);
if(dfn[x]<low[to])is[id]=is[id^1]=1;
low[x]=min(low[x],low[to]);
}
else low[x]=min(low[x],dfn[to]);
}
return;
}
void DFS(int x,int now){
if(vis[x])return;
vis[x]=1,dccV[now]++,in[x]=now;
for(int i=0;i<v[x].size();i++){
int to=v[x][i].to,id=v[x][i].id;
if(is[id])continue;
DFS(to,now);
}
return;
}
void dfs(int x,int fa){
siz[x]=dccE[x];
for(int i=0;i<g[x].size();i++){
int to=g[x][i];
if(to==fa)continue;
dfs(to,x);
siz[x]+=siz[to]+1;
}
return;
}
void DP(int x,int fa){
for(int i=0;i<g[x].size();i++){
int to=g[x][i];
if(to==fa)continue;
DP(to,x);
dp[x][1]=(dp[to][1]*dp[x][0]%mod+(dp[to][0]*2%mod+dp[to][1])%mod*dp[x][1]%mod)%mod,dp[x][1]%=mod;
dp[x][0]=dp[x][0]*dp[to][0]*2%mod,dp[x][0]%=mod;
}
if(x==1)ans+=dp[x][1],ans%=mod;
else ans+=dp[x][1]*fpow(2,siz[1]-siz[x]-1,mod)%mod,ans%=mod;
return;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++){
int x,y;
cin>>x>>y;
if(x==y)continue;
e[i]={x,y};
v[x].push_back({y,ID(i)});
v[y].push_back({x,ID(i)+1});
}
for(int i=1;i<=n;i++)if(!dfn[i])Tarjan(i,-1);
for(int i=1;i<=n;i++)if(!vis[i])DFS(i,++col);
for(int i=1;i<=m;i++){
if(e[i].x==e[i].y)continue;
if(in[e[i].x]!=in[e[i].y])
g[in[e[i].x]].push_back(in[e[i].y]),g[in[e[i].y]].push_back(in[e[i].x]);
else dccE[in[e[i].x]]++;
}
for(int i=1;i<=col;i++)
dp[i][0]=fpow(2,dccE[i],mod),dp[i][1]=(fpow(2,dccE[i]+dccV[i],mod)-dp[i][0]+mod)%mod;
dfs(1,0),DP(1,0);
cout<<ans;
return 0;
}后记
再放几道题吧,但是不想写解析了。
- P3177 [HAOI2015] 树上染色
- P4362 [NOI2002] 贪吃的九头龙
- P1270 “访问”美术馆
下一章节应该要写换根 dp 了,想摆。
注:换根 DP 不知道咕咕咕了多久了,干脆不写了嘿嘿。