线性基学习笔记
xtx1092515503
·
·
个人记录
如果有线性代数基础的话会更易理解。推荐配合本人的线性代数学习笔记食用。
线性基是针对某个序列生成的一个集合,它具有以下两条性质:
-
线性基中任意选择一些数的异或值所构成的集合,等于原序列中任意选择一些数的异或值所构成的集合。
-
线性基是满足上述条件的最小集合。
有了上面这两条性质,我们便可以得出如下几条推论:
-
原序列中任何数,都可以由线性基中一些数异或起来得到(由性质1直接得出)
-
线性基中不存在一组数,使得它们的异或值为0(如果存在x\operatorname{xor}y\operatorname{xor}z=0,它就等价于x\operatorname{xor}y=z,就可以删掉z使得异或集合不变,违背了性质2)
-
线性基中不存在两组取值集合,使得它们的异或和相等(不然你把这两个集合异或在一起就会得到异或和为0的集合)
现在介绍线性基的构建方法:
我们用x_{(2)}表示x的二进制表示,用d_x表示线性基数组。
当$d_x$不为$0$时,表明这一位上储存了一个线性基。
$(d_x)_{(2)}$的第$x$位一定为$1$,且第$x+1$位往后全都为$0$。
这是它的构造方式(向序列中插入一个数$x$):
```cpp
void ins(ll x){
for(int i=55;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];//eliminate the 1 on the i-th bit of x
else{d[i]=x;break;}//successfully inserted, jump out.
}
}
```
这是什么意思呢?
我们要**尽量把$x$异或到**$0$,因为一旦异或到$0$就表明$x$可以被线性基表示出来,就不用加入线性基了。
如果$x$的第$i$位是$0$,你要这时候异或上去了$d_i$,它的第$i$位就是$1$了,这个$1$以后消不掉($i$是$d_i$的最高位),故直接跳掉。
如果$x$的第$i$位是$1$,这时候必须异或上$d_i$才能消掉这一位(以后消不掉),不管对之后位数的影响。
那如果这时的$d_i$不存在呢?很显然这时$x$不能被线性基中的数表示出来,因此要把$x$加入线性基。
那什么时候这个$x$不会被加入线性基呢?很显然,当某次异或之后,$x$变成了$0$。则此时$x$可以被集合中数表示出来,可以不加入。
这就是构建线性基的方式。
**注意数据范围!当它是```long long```范围时,记得写```1ll<<x```而非```1<<x```!**
------------
很明显,构造线性基的复杂度是$O(n\log a_i)$的,其中$n$为插入数的个数,$a_i$为插入的数。
但是,当$a_i$很大(比如说$2^{1000}$级别)的时候,你就不得不使用```bitset```来代替,此时复杂度就是$O(n\dfrac{\log^2a_i}{w})$,其中$w$是```bitset```常数。```bitset```具体的实现在我们接下来的例题4.3.[[HAOI2017]八纵八横]中可以看到。
一般不会有毒瘤出题人卡线性基时间复杂度的,毕竟(位运算/```bitset```+循环)让它的效率极高,并且它也没有过多变形(不像线段树什么的),所以一般不用担心复杂度。
------------
另,线性基还有一种构建方式是通过高斯消元。初学者可以直接跳到下方的Part1开始阅读(因为高斯消元的解法在下文所有代码中都没有出现——不在线、跑得慢,谁会喜欢用这玩意呀!)
接下来出现的所有名词都是线性代数专有名词,所以推荐配合本人的[线性代数学习笔记](https://www.luogu.com.cn/blog/Troverld/linear-algebra)食用。
假设所有元素的值域都在 $2^k$ 以内。则,其可被看作一个 $k$ 维向量,通过异或操作张成一个空间。
一组空间的基的大小,等价于将其中所有向量并作一个矩阵后,其中的主元列数量。
于是我们对该矩阵作高斯消元即可求出其所有主元列。因为线性基具有异或等价性,所以无论是原矩阵上的主元列,还是行变换后的主元列,都是一组合法的基底。
但是,此方法是离线的。
由上述结论也可发现,线性基的大小最多是 $k$。
------
更多操作随着例题会逐步解锁。
# Part1. 线性基基础操作
## I.求$\max$异或值(即[【模板】线性基](https://www.luogu.com.cn/problem/P3812))
从高位往低位枚举$d_i$,维护一个答案$res$。如果$res$异或上$d_i$更优,则异或。
显然,如果$res$的第$i$位是$1$,这时肯定不会异或——不然就把这个$1$给消去了,而就算之后的位上全是$1$,也抵不上这里的一个$1$(考虑类比01trie的贪心)。
而如果这位上是$0$,则一定要异或上$d_i$将这位变成$1$。
因此最终呈现出来的结果就是能异或就异或。(注意异或的优先级是要劣于小于号的优先级的,故记得加括号)
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n;
ll a[100],d[100],res;
void ins(ll x){
for(int i=55;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];//eliminate the 1 on the i-th bit of x
else{d[i]=x;break;}//successfully inserted, jump out.
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%lld",&a[i]),ins(a[i]);
for(int i=55;i>=0;i--)if((res^d[i])>res)res^=d[i];
printf("%lld\n",res);
return 0;
}
```
## II.求$\min$异或值
显然,当某次插入失败时,答案即为$0$。
而当没有任何插入失败时,答案为$\min\{d_i\}$(这点可以在我们接下来的$k$小异或和中看得更清楚)
## III.求第$k$小异或和(即[LOJ#114.k大异或和](https://loj.ac/problem/114))
我们首先建出线性基出来。
注意到线性基是**非唯一**的——我们随便拿线性基中任意两个数异或到一起,就可以得到新的一组线性基。
而在这所有线性基中,我们这里要用的便是**所有$d_x$最小的那一组**。
构造方法很简单——从小到大枚举所有$d_i$,从大到小枚举所有$j<i$,如果$d_i\operatorname{xor}d_j<d_i$,就$\operatorname{xor}$掉。
在这里,我们就可以看出$\min$异或值为什么是$\min\{d_i\}$了:因为$\min\{d_i\}$即是$i$最小的那个$d_i$,它不存在一个$j$可以跟它异或,故它的值不会变化,一直是最小值。
这么全部搞完之后,我们得到一组新的线性基。这组线性基具有一个性质:
$$\forall i>j,d_i\operatorname{xor}d_j>d_i$$
因此我们只需要求出从小到大所有的不为$0$的$d_i$,记其数量为$tot$。如果$tot\neq n$,就意味着有数没有被插入线性基,存在一个$0$作为异或和,$k$应该减一;然后,如果$k\geq 2^{tot}$,就意味着全部异或和数量小于$k$,输出$-1$;否则,找出$k_{(2)}$中所有非$0$位,计算对应位置(指第$x$个**非零**的线性基)的$d_x$的异或和即可。
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,d[64],arr[64],tot;
void ins(int x){
for(int i=55;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;break;}
}
}
void rebuild(){
for(int i=0;i<=55;i++)for(int j=i-1;j>=0;j--)if(d[i]&(1ll<<j))d[i]^=d[j];
for(int i=0;i<=55;i++)if(d[i])arr[tot++]=i;
}
signed main(){
scanf("%lld",&n);
for(int i=1,x;i<=n;i++)scanf("%lld",&x),ins(x);
rebuild(),scanf("%lld",&m);
for(int i=1,x,res;i<=m;i++){
scanf("%lld",&x),res=0;
if(tot<n)x--;
if(x>=(1ll<<tot)){puts("-1");continue;}
for(int j=0;j<tot;j++)if(x&(1ll<<j))res^=d[arr[j]];
printf("%lld\n",res);
}
return 0;
}
```
## IV.线性基合并(即[[SCOI2016]幸运数字](https://www.luogu.com.cn/problem/P3292))
~~题解区用点分治的、用树剖的是什么神仙啦,这题根本不需要呀~~
线性基真是太可爱了,这几题省选题我都没有看题解,果然是又好想又好写。
线性基具有**可并性**,即你可以合并两块线性基得到一块更大的线性基,合并方式是将一块线性基中所有东西暴力插入另一块,复杂度$O(\log^2)$。
于是我们便很轻松地可以把线性基模板化掉:
```cpp
struct lb{//linear basis?
ll d[64];
void print(){
for(int i=0;i<=62;i++)if(d[i])printf("%d:%lld\n",i,d[i]);
}
lb(){memset(d,0,sizeof(d));}
void operator +=(ll x){
for(int i=62;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;break;}
}
}
ll& operator [](int x){
return d[x];
}
void operator +=(lb &x){
for(int i=62;i>=0;i--)if(x[i])*this+=x[i];
}
friend lb operator +(lb &x,lb &y){
lb z=x;
for(int i=62;i>=0;i--)if(y[i])z+=y[i];
return z;
}
ll calc(){//calculate maximum possible
ll res=0;
for(int i=62;i>=0;i--)if((res^d[i])>res)res^=d[i];
return res;
}
};
```
回到这道题。首先,关于路径,肯定会想到**求LCA**,而求LCA的方法之一便是**倍增**。因此我们只需要预处理倍增线性基即可在求LCA的同时求出线性基了。
复杂度$O(n\log n\log g)$。
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,m,anc[20100][16],dep[20100];
ll val[20100];
struct lb{//linear basis?
ll d[64];
void print(){
for(int i=0;i<=62;i++)if(d[i])printf("%d:%lld\n",i,d[i]);
}
lb(){memset(d,0,sizeof(d));}
void operator +=(ll x){
for(int i=62;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;break;}
}
}
ll& operator [](int x){
return d[x];
}
void operator +=(lb &x){
for(int i=62;i>=0;i--)if(x[i])*this+=x[i];
}
friend lb operator +(lb &x,lb &y){
lb z=x;
for(int i=62;i>=0;i--)if(y[i])z+=y[i];
return z;
}
ll calc(){
// print();
ll res=0;
for(int i=62;i>=0;i--)if((res^d[i])>res)res^=d[i];
return res;
}
}LB[20100][16];
vector<int>v[20100];
void dfs(int x){
LB[x][0]+=val[x];
for(int y:v[x])if(y!=anc[x][0])dep[y]=dep[x]+1,anc[y][0]=x,dfs(y);
}
ll query(int x,int y){
lb z;
if(dep[x]<dep[y])swap(x,y);
for(int i=15;i>=0;i--)if(dep[x]-(1<<i)>=dep[y])z+=LB[x][i],x=anc[x][i];
if(x==y){z+=val[x];return z.calc();}
for(int i=15;i>=0;i--)if(anc[x][i]!=anc[y][i])z+=LB[x][i],z+=LB[y][i],x=anc[x][i],y=anc[y][i];
z+=LB[x][0];
z+=LB[y][0];
z+=val[anc[x][0]];
return z.calc();
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%lld",&val[i]);
for(int i=1,x,y;i<n;i++)scanf("%d%d",&x,&y),v[x].push_back(y),v[y].push_back(x);
dfs(1);
for(int j=1;j<=15;j++)for(int i=1;i<=n;i++)anc[i][j]=anc[anc[i][j-1]][j-1],LB[i][j]=LB[i][j-1]+LB[anc[i][j-1]][j-1];
for(int x,y;m--;)scanf("%d%d",&x,&y),printf("%lld\n",query(x,y));
return 0;
}
```
------------
# Part2.线性基上排序与贪心
## I.[[BJWC2011]元素](https://www.luogu.com.cn/problem/P4570)
还记得我们之前说的吗?
```
性质2.线性基是满足上述条件的最小集合。
推论4.线性基中不存在一组数,使得它们的异或值为0
```
因为我们在构建线性基的时候,并**不存在将元素移出线性基**的行为,而无论怎么搞线性基最终的大小都是一定的,故我们直接将元素按照魔力值从大到小加入线性基,如果成功就增加魔力值即可。
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,res;
ll d[100];
bool ins(ll x){
for(int i=62;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;return true;}
}
return false;
}
pair<int,ll>p[1010];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%lld%d",&p[i].second,&p[i].first);
sort(p+1,p+n+1);
for(int i=n;i;i--)if(ins(p[i].second))res+=p[i].first;
printf("%d\n",res);
return 0;
}
```
## II.[[CQOI2013] 新Nim游戏](https://www.luogu.com.cn/problem/P4301)
回忆起NIM游戏先手必胜当且仅当**所有石子堆的异或和不为$0$**。
我们可以发现,这题**先手必然必胜**——因为先手第一次总是可以取到只剩一堆石子,然后后手第一次就什么也取不了,然后先手第二次就可以直接取掉剩下那一堆。
从上面那个思路中,我们发现先手的目标肯定是**去掉一些数,使得剩下的数不存在异或和为$0$的非空子集**。不然,对手肯定就直接把除了那个非空子集外其它东西全部取光,先手就必败了。
不存在异或和为$0$的非空子集,这好像意味着**序列中所有数都可以被插入一个线性基**!
因此我们就直接照着2.1.[[BJWC2011]元素](https://www.luogu.com.cn/problem/P4570),排序后插入线性基即可。
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,a[110],d[110];
ll res;
bool ins(ll x){
for(int i=31;i>=0;i--){
if(!(x&(1<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;return true;}
}
return false;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
sort(a+1,a+n+1);
for(int i=n;i;i--)if(!ins(a[i]))res+=a[i];
printf("%lld\n",res);
return 0;
}
```
------------
# Part3.每个异或值出现了多少次
## I.[[TJOI2008]彩灯](https://www.luogu.com.cn/problem/P3857)
那个“亮变暗,暗变亮”刚好是异或的定义。
在建出线性基后,我们翻到开头,有:
```
性质1.线性基中任意个数的异或值所构成的集合,等于原序列中任意个数的异或值所构成的集合。
推论5.线性基中不存在两组取值集合,使得它们的异或和相等
```
这就意味着线性基中总共$2^{tot}$种取值,就刚好等于原数组的所有异或值的可能。
因此答案即为$2^{tot}$。
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,m,tot;
ll d[100];
char s[100];
void ins(){
ll x=0;
for(int i=0;i<n;i++)x=(x<<1)+(s[i]=='O');
for(int i=n-1;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x,tot++;break;}
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)scanf("%s",s),ins();
printf("%lld\n",(1ll<<tot)%2008);
return 0;
}
```
## II.[albus就是要第一个出场](https://www.luogu.com.cn/problem/P4869)
打开这题,我们发现它和[LOJ#114.k大异或和](https://loj.ac/problem/114)长得惊人的类似,就是一个是求排第几的是谁,一个是求它排第几而已。
这种位置和次序互相转换的题,一般来说**套个二分**就能解决。
但是这里的集合是**可重集**,咋办呢?
没关系!我们之前一开始得出了一条推论:
```
推论5.线性基中不存在两组取值集合,使得它们的异或和相等。
```
而我们可以把所有加入线性基失败的数看作$0$(之前说过,线性基内部任意两个数互相异或得到的新集合仍然是一组线性基;如果把加入失败的数也看做加入了线性基,则多次异或后最终可以看作是$0$)。
则原序列的集合中所有数都出现了$2^{n-tot}$次(因为一共有$n-tot$个$0$,从中选出任意多个异或在一起仍然是$0$,再跟另一个数异或起来,就会发现每个数都出现了$2^{n-tot}$次)。
故我们直接套上二分后答案乘上$2^{n-tot}$即可。
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
const int mod=10086;
int n,m,d[40],arr[40],tot;
void ins(int x){
for(int i=31;i>=0;i--){
if(!(x&(1<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;break;}
}
}
void rebuild(){
for(int i=0;i<=31;i++)for(int j=i-1;j>=0;j--)if(d[i]&(1<<j))d[i]^=d[j];
for(int i=0;i<=31;i++)if(d[i])arr[tot++]=i;
}
int query(int ip){
int res=0;
for(int i=tot-1;i>=0;i--)if(ip&(1<<i))res^=d[arr[i]];
return res;
}
int ksm(int x,int y){
int z=1;
for(;y;x=1ll*x*x%mod,y>>=1)if(y&1)z=1ll*x*z%mod;
return z;
}
signed main(){
scanf("%d",&n);
for(int i=1,x;i<=n;i++)scanf("%d",&x),ins(x);
rebuild();
scanf("%d",&m);
int l=0,r=(1<<tot)-1;
while(l<r){
int mid=(l+r+1)>>1;
if(query(mid)<=m)l=mid;
else r=mid-1;
}
printf("%d\n",(1ll*ksm(2,n-tot)*l+1)%mod);
return 0;
}
```
## III.[CF959F Mahmoud and Ehab and yet another xor task](https://www.luogu.com.cn/problem/CF959F)
~~这名字真长~~
可以发现这题实际上和上题类似,仍然只是求出$2^{n-tot}$即可。
但是这道题是多组询问,还是针对**前缀**的!
这里就有两种方法:
1. 离线下来,然后一遍扫过即可。
2. 可持久化线性基。
~~不要以为是什么高大上的东西,可持久化线性基就直接copy一遍数组即可,复杂度$O(n\log a_i)$,因为你求线性基的时候总是免不了遍历一遍数组的~~。
代码(离线做法):
```cpp
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
int n,m,a[100100],d[30],res[100100],tot,pov[100100];
bool ins(int x){
for(int i=22;i>=0;i--){
if(!(x&(1<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;return true;}
}
return false;
}
bool find(int x){
for(int i=22;i>=0;i--){
if(!(x&(1<<i)))continue;
if(d[i])x^=d[i];
else return false;
}
return true;
}
vector<pair<int,int> >v[100100];
int main(){
scanf("%d%d",&n,&m),pov[0]=1;
for(int i=1;i<=n;i++)scanf("%d",&a[i]),pov[i]=(pov[i-1]<<1)%mod;
for(int i=1,x,y;i<=m;i++)scanf("%d%d",&x,&y),v[x].push_back(make_pair(y,i));
for(int i=1;i<=n;i++){
tot+=ins(a[i]);
for(auto j:v[i])res[j.second]=pov[i-tot]*find(j.first);
}
for(int i=1;i<=m;i++)printf("%d\n",res[i]);
return 0;
}
```
## IV.[CF895C Square Subsets](https://www.luogu.com.cn/problem/CF895C)
~~听说这题有用状压的神仙,orzorz~~
首先,因为$a_i$的范围很小($70$),我们可以很轻松地想到要与$a_i$范围内的质数有关。
人脑枚举一下后,我们发现$70$以内的质数有:
$2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67$,共$19$个。
因为最终的乘积为完全平方数,当且仅当**每个质数在乘积中出现了偶数次**,所以我们可以很轻松地把每个$a_i$转成**每个质数出现了奇数次还是偶数次**的一个```bitmask```。
发现两个数乘在一起,就相当于把它们的```bitmask```异或起来。则只有一堆数的```bitmask```的异或和为$0$,它们的积才是完全平方数。这不就是前几题的内容吗?
然后直接把它丢入线性基,则答案即为$2^{n-tot}-1$(这题不能选空集)。
另外还有一道双倍经验的题是[ACMSGURU 200. Cracking RSA ](https://codeforces.ml/problemsets/acmsguru/problem/99999/200),只不过那题的答案可能爆```long long```,CF又不给用```__int128```,故只能用两个```unsigned long long```来模拟```___int128```。
代码(CF895C的,双倍经验那题只需要换成```bitset```然后再把答案用两个```ull```装就行了):
```cpp
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
int n,pri[22]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67},tot,pov[100100],d[20];
bool ins(int x){
for(int i=20;i>=0;i--){
if(!(x&(1<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;return true;}
}
return false;
}
int main(){
scanf("%d",&n),pov[0]=1;
for(int i=1,x,y;i<=n;i++){
scanf("%d",&x),y=0;
for(int j=0;j<19;j++){
if(x%pri[j])continue;
int z=0;
while(!(x%pri[j]))x/=pri[j],z^=1;
y|=(z<<j);
}
tot+=ins(y);
pov[i]=(pov[i-1]<<1)%mod;
}
printf("%d\n",pov[n-tot]-1);
return 0;
}
```
------------
## V.[TopCoder13145-PerfectSquare](https://vjudge.net/problem/TopCoder-13145)
和前几题类似。我们仍然选择将每个数质因数分解,然后将其转换为一个 `01` 串。
然而这题还有一个限制,即每行每列都只能取奇数个东西。
于是我们额外在每个 `01` 串前面添上 $2n$ 位,表示当前的元素位于哪一行哪一列,然后建出线性基。最后,只要查询除了前 $2n$ 位是 $1$,其它位都是 $0$ 的串是否在线性基内出现,且出现了多少次即可。
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
const int lim=40000;
const int LEN=1020;
const int mod=1e9+7;
#define BIT bitset<LEN>
class PerfectSquare{
private:
int a[30][30],n,m,nul;
BIT bs[LEN];
map<int,int>mp;
int pri[40100];
void Eular(){
for(int i=2;i<=lim;i++){
if(!pri[i])pri[++pri[0]]=i;
for(int j=1;j<=pri[0]&&i*pri[j]<=lim;j++){
pri[i*pri[j]]=true;
if(!(i%pri[j]))break;
}
}
}
void ins(BIT &x){
for(int i=m-1;i>=0;i--){
if(!x[i])continue;
if(bs[i][i])x^=bs[i];
else{bs[i]=x;return;}
}
nul++;
}
bool find(BIT &x){
for(int i=m-1;i>=0;i--){
if(!x[i])continue;
if(bs[i][i])x^=bs[i];
}
return x.none();
}
public:
int ways(vector<int>v){
n=sqrt(v.size())+0.1,Eular();
for(int i=0;i<n;i++)for(int j=0;j<n;j++)a[i][j]=v[i*n+j];
m=2*n;
for(int i=0;i<n;i++)for(int j=0;j<n;j++){
BIT x;
x[i]=true,x[n+j]=true;
for(int k=1;k<=pri[0];k++){
if(a[i][j]%pri[k])continue;
if(!mp[pri[k]])mp[pri[k]]=m++;
while(!(a[i][j]%pri[k]))x.flip(mp[pri[k]]),a[i][j]/=pri[k];
}
if(a[i][j]!=1){
if(!mp[a[i][j]])mp[a[i][j]]=m++;
x.flip(mp[a[i][j]]);
}
ins(x);
}
BIT x;
for(int i=0;i<2*n;i++)x[i]=true;
if(!find(x))return 0;
int ret=1;
for(int i=0;i<nul;i++)(ret<<=1)%=mod;
return ret;
}
}my;
```
# Part4.线性基在图论方面的应用
## I.[[WC2011]最大XOR和路径](https://www.luogu.com.cn/problem/P4151)
~~就我一个人一开始只想到二进制分解按位处理然后没写出来吗~~
显然,这题的路径**不是简单路径**,它可以有重点重边。但是,如果我们对于所有边求异或和的话,你会惊奇的发现有贡献的边**只有一条从$1$到$n$的主路径和许多环**!
我们可以看一张图:
路径上的红边都经过了一次,而蓝边却经过了两次,被消掉了!
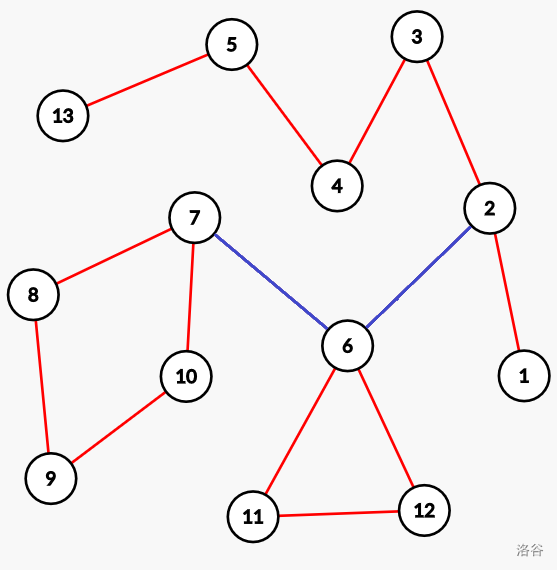
所以我们可以先一遍dfs求出所有环的异或和丢入线性基,然后再用一条$1\rightarrow n$的路径的异或和从中找到最大异或和即可。
至于找哪条路径呢?随便找,反正任何两条$1\rightarrow n$的路径都会构成一个环,在线性基里如果更优就被异或掉了。
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,m,head[50100],cnt;
ll dis[50100];
struct lb{//linear basis?
ll d[64];
void print(){
for(int i=0;i<=62;i++)if(d[i])printf("%d:%lld\n",i,d[i]);
}
lb(){memset(d,0,sizeof(d));}
void operator +=(ll x){
for(int i=62;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;break;}
}
}
ll& operator [](int x){
return d[x];
}
void operator +=(lb &x){
for(int i=62;i>=0;i--)if(x[i])*this+=x[i];
}
friend lb operator +(lb &x,lb &y){
lb z=x;
for(int i=62;i>=0;i--)if(y[i])z+=y[i];
return z;
}
ll calc(ll x){//calculate maximum possible
ll res=x;
for(int i=62;i>=0;i--)if((res^d[i])>res)res^=d[i];
return res;
}
}LB;
struct node{
int to,next;
ll val;
}edge[200100];
void ae(int u,int v,ll w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
bool vis[50100];
void dfs(int x){
for(int i=head[x];i!=-1;i=edge[i].next){
if(!vis[edge[i].to])vis[edge[i].to]=true,dis[edge[i].to]=dis[x]^edge[i].val,dfs(edge[i].to);
else LB+=dis[x]^dis[edge[i].to]^edge[i].val;
}
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head));
for(ll i=1,x,y,z;i<=m;i++)scanf("%lld%lld%lld",&x,&y,&z),ae(x,y,z);
dfs(1);
printf("%lld\n",LB.calc(dis[n]));
return 0;
}
```
## II.[CF845G Shortest Path Problem?](https://www.luogu.com.cn/problem/CF845G)
嗯,这题跟上一题一样,就是上题是求$\max$,这题是求$\min$。
在线性基中寻找最小异或和(不是1.2中那个,因为这题是找**关于$1\rightarrow n$路径异或和**的最小异或和),就跟最大异或和一样——从高位到低位枚举$d_i$,假如异或起来更小,就异或掉。
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
int n,m,head[100100],cnt,dis[100100];
struct lb{//linear basis?
int d[40];
void print(){
for(int i=0;i<=30;i++)if(d[i])printf("%d:%d\n",i,d[i]);
}
lb(){memset(d,0,sizeof(d));}
void operator +=(int x){
for(int i=30;i>=0;i--){
if(!(x&(1<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;break;}
}
}
int& operator [](int x){
return d[x];
}
void operator +=(lb &x){
for(int i=30;i>=0;i--)if(x[i])*this+=x[i];
}
friend lb operator +(lb &x,lb &y){
lb z=x;
for(int i=30;i>=0;i--)if(y[i])z+=y[i];
return z;
}
int calc(int x){//calculate minimum possible
int res=x;
for(int i=30;i>=0;i--)if((res^d[i])<res)res^=d[i];
return res;
}
}LB;
struct node{
int to,next,val;
}edge[200100];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
bool vis[100100];
void dfs(int x){
for(int i=head[x];i!=-1;i=edge[i].next){
if(!vis[edge[i].to])vis[edge[i].to]=true,dis[edge[i].to]=dis[x]^edge[i].val,dfs(edge[i].to);
else LB+=dis[x]^dis[edge[i].to]^edge[i].val;
}
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head));
for(int i=1,x,y,z;i<=m;i++)scanf("%d%d%d",&x,&y,&z),ae(x,y,z);
dfs(1);
// LB.print();
printf("%d\n",LB.calc(dis[n]));
return 0;
}
```
## III.[[HAOI2017]八纵八横](https://www.luogu.com.cn/problem/P3733)
在这题,我们将会介绍**可删除线性基**,离线和在线两种做法。因为篇幅有点长,可以参见笔者的[题解](https://www.luogu.com.cn/blog/Troverld/solution-p3733),此处不再赘述。
## IV.[CF938G Shortest Path Queries](https://www.luogu.com.cn/problem/CF938G)
请务必先把前一道题的题解看完——在那里面介绍的可删除线性基,是我们这题仍然需要用的。
在那篇题解中,我还用**LCT维护动态图的连通性**来类比了可删除线性基,然后这题我们就真的要来用LCT维护了!
不会LCT的可以左转[LCT学习笔记](https://www.luogu.com.cn/blog/Troverld/lct-gan-xing-xia-che),不知道怎么维护连通性的参见该笔记的XVI.[二分图 /【模板】线段树分治](https://www.luogu.com.cn/problem/P5787)。
我们这题就要用LCT先来维护连通性。因为在上一题中,**“公路”是永远不会被删除的**,我们求出两点间距离可以直接使用公路的结果,所以上一题不需要LCT;但是这题没有一棵始终存在的生成树,只保证它始终联通,故为了求出两点间距离,我们需要使用LCT。
因为LCT和线性基中维护的都是何时这条边/这个线性基会被删除,所以可以很方便地嫁接在一起,只需要在成环时将环的异或值加入线性基即可。复杂度$O(n\log n)$。
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
int n,m,q,qwq;
pair<int,int>p[200100];
struct edge{
int x,y,z,st,ed;
}e[400100];
//-----------------------Linear Basis Below----------------
int tms[40],d[40];
void ins(int now,int x){
for(int i=30;i>=0;i--){
if(!(x&(1<<i)))continue;
if(tms[i]<now)swap(tms[i],now),swap(x,d[i]);
if(!now)break;
x^=d[i];
}
}
int ask(int now,int x){
for(int i=30;i>=0;i--)if(tms[i]>now&&(x^d[i])<x)x^=d[i];
return x;
}
void print(){
for(int i=0;i<=30;i++)if(d[i])printf("%d:%d\n",i,d[i]);
}
//------------------Linear Basis Above---------------------
//------------------LCT Below------------------------------
#define lson t[x].ch[0]
#define rson t[x].ch[1]
struct LCT{
int fa,ch[2],mn,del,sum,val;
bool rev;
}t[600100];
inline int identify(int x){
if(x==t[t[x].fa].ch[0])return 0;
if(x==t[t[x].fa].ch[1])return 1;
return -1;
}
inline void pushup(int x){
t[x].mn=x;
t[x].sum=t[x].val;
if(lson){
if(t[t[x].mn].del>t[t[lson].mn].del)t[x].mn=t[lson].mn;
t[x].sum^=t[lson].sum;
}
if(rson){
if(t[t[x].mn].del>t[t[rson].mn].del)t[x].mn=t[rson].mn;
t[x].sum^=t[rson].sum;
}
}
inline void REV(int x){
t[x].rev^=1,swap(lson,rson);
}
inline void pushdown(int x){
if(!t[x].rev)return;
if(lson)REV(lson);
if(rson)REV(rson);
t[x].rev=0;
}
inline void rotate(int x){
register int y=t[x].fa;
register int z=t[y].fa;
register int dirx=identify(x);
register int diry=identify(y);
register int b=t[x].ch[!dirx];
if(diry!=-1)t[z].ch[diry]=x;t[x].fa=z;
if(b)t[b].fa=y;t[y].ch[dirx]=b;
t[y].fa=x,t[x].ch[!dirx]=y;
pushup(y),pushup(x);
}
inline void pushall(int x){
if(identify(x)!=-1)pushall(t[x].fa);
pushdown(x);
}
inline void splay(int x){
pushall(x);
while(identify(x)!=-1){
register int fa=t[x].fa;
if(identify(fa)==-1)rotate(x);
else if(identify(x)==identify(fa))rotate(fa),rotate(x);
else rotate(x),rotate(x);
}
}
inline void access(int x){for(register int y=0;x;x=t[y=x].fa)splay(x),rson=y,pushup(x);}
inline void makeroot(int x){access(x),splay(x),REV(x);}
inline int split(int x,int y){makeroot(x),access(y),splay(y);return t[y].sum;}
inline void link(int x,int y){makeroot(x),t[x].fa=y;}
inline void cut(int x,int y){split(x,y),t[y].ch[0]=t[x].fa=0,pushup(y);}
inline int findroot(int x){
access(x),splay(x);
pushdown(x);
while(lson)x=lson,pushdown(x);
splay(x);
return x;
}
inline void LINK(int ip){
t[ip+n].val=e[ip].z;
t[ip+n].del=e[ip].ed;
pushup(ip+n);
if(findroot(e[ip].x)!=findroot(e[ip].y)){link(e[ip].x,ip+n),link(e[ip].y,ip+n);return;}
split(e[ip].x,e[ip].y);
int id=t[e[ip].y].mn;
if(t[id].del>t[ip+n].del){ins(t[ip+n].del,t[e[ip].y].sum^t[ip+n].val);return;}
cut(e[id-n].x,id),cut(e[id-n].y,id);
link(e[ip].x,ip+n),link(e[ip].y,ip+n);
ins(t[id].del,split(e[id-n].x,e[id-n].y)^t[id].val);
}
//-----------------LCT above-------------------------------
map<pair<int,int>,int>mp;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)t[i].del=0x3f3f3f3f,t[i].val=0;
for(int i=1;i<=m;i++)scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].z),mp[make_pair(e[i].x,e[i].y)]=i;
scanf("%d",&q);
for(int i=1,tp,x,y,z;i<=q;i++){
scanf("%d%d%d",&tp,&x,&y);
if(tp==1)scanf("%d",&z),++m,e[m].x=x,e[m].y=y,e[m].z=z,e[m].st=i,mp[make_pair(x,y)]=m;
if(tp==2)e[mp[make_pair(x,y)]].ed=i,mp.erase(make_pair(x,y));
if(tp==3)p[i]=make_pair(x,y);
}
for(int i=1;i<=m;i++)if(!e[i].ed)e[i].ed=q+1;
// for(int i=1;i<=m;i++)printf("(%d,%d,%d):[%d,%d]\n",e[i].x,e[i].y,e[i].z,e[i].st,e[i].ed);
for(int i=1,j=1;i<=q;i++){
while(j<=m&&e[j].st<=i)LINK(j++);
if(p[i]!=make_pair(0,0))printf("%d\n",ask(i,split(p[i].first,p[i].second)));
}
return 0;
}
```
------------
# Part5.线性基可形成的所有不同异或值的和
## I.[CF724G Xor-matic Number of the Graph](https://www.luogu.com.cn/problem/CF724G)
~~这题整整卡了我5个小时,心态崩溃~~。
首先,我们先来考虑一下,线性基中所有异或和的和是什么呢?
我们考虑按位处理。对于第$i$位,只有**所有第$i$位为$1$的**$d_x$才会影响这一位的取值。
设共有$k$个第$i$位为$1$的$d_x$,且一共有$tot$个非零的$d_x$。则那$tot-k$个第$i$位为$0$的$d_x$,**无论选不选,都不会有影响**,故共$2^{tot-k}$种方案。而那$k$个第$i$位为$1$的$d_x$,只有选择**奇数**个,最终才会留下一个$1$。
则所有最终异或和中第$i$位为$1$的方案数量为:
$2^{tot-k}\times\sum\limits_{j\operatorname{mod}2\equiv1}C_k^j
我们又有\sum\limits_{j\operatorname{mod}2\equiv1}C_k^j=\begin{cases}0\ (k=0)\\2^{k-1}\ (k>0)\end{cases}
故2^{tot-k}\times\sum\limits_{j\operatorname{mod}2\equiv1}C_k^j=\begin{cases}0\ (k=0)\\2^{tot-1}\ (k>0)\end{cases}
于是我们发现只要存在一个d_x的第i位上为1,这位上就会有2^{tot-1}种方案(即半数方案)异或值为1。而如果不存在这样一个d_x,则这位上无论如何都是0。
因此我们只需要求出所有非零的d_x \operatorname{or}在一起的结果,这个结果的非0位有2^{tot-1}种方式做出贡献。因此总答案即为(\bigvee\limits_{d_i\neq 0}d_i)\times 2^{tot-1}。
现在我们回到本题。很明显,同前几题一样,仍然可以搜出所有的环并丢入线性基中。但是这回,因为(u,v)不是唯一的,这是否意味着我们要暴力每一组(u,v),然后到线性基中求值呢?
不需要。我们发现如果设节点i到某个指定节点的距离为dis_i的话,则u到v的距离实际上就是dis_u\operatorname{xor}dis_v。
因此我们实际上是从集合\{dis_i\}中选择任意两个值异或在一起并在线性基中求值。但是这回我们不是求线性基中所有东西的异或和了——而是求线性基中所有东西的(异或和再异或上(dis_u\operatorname{xor}dis_v))的和。
我们可以把该集合中所有数放在一起,一起按位求值。
我们设一个tmp=\bigvee\limits_{d_i\neq 0}d_i。则tmp的第i位如果为1,则它有一半的方案为0,一半的方案为1,因此会对集合\{dis_i\}中每一对数都能产生2^{tot-1}种方案。设此集合大小为sz,则共2^{tot-1}\times\dfrac{sz(sz-1)}{2}种方案。
而如果tmp的第i位为0的话,无论如何异或和的第i位都是0,因此只有在集合\{dis_i\}选取两个第i位不同的数拼一起最终结果才是1。设\{dis_i\}中共有cnt个数第i位是1,则共有2^{tot}\times cnt\times(sz-cnt)种方案。
最终的统计答案函数:
int calc(){
ll tmp=0;
int ret=0,sz=v.size();
for(int i=62;i>=0;i--)if(d[i])tmp|=d[i];
for(int i=62;i>=0;i--){
int cnt=0;
for(ll j:v)cnt+=((j>>i)&1);
if(tmp&(1ll<<i))(ret+=((1ll<<i)%mod)*((1ll<<(tot-1))%mod)%mod*((1ll*sz*(sz-1)/2)%mod)%mod)%=mod;
else(ret+=((1ll<<i)%mod)*((1ll<<tot)%mod)%mod*(1ll*cnt*(sz-cnt)%mod)%mod)%=mod;
}
return ret;
}
然后只要注意这张图可能不连通,要对于每个连通块分开讨论即可。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
int n,m,head[101000],cnt,res;
ll dis[101000];
vector<ll>v;
struct lb{//linear basis?
ll d[64];
int tot;
void print(){
for(int i=0;i<=62;i++)if(d[i])printf("%d:%lld\n",i,d[i]);
}
void clear(){memset(d,0,sizeof(d)),tot=0;}
lb(){memset(d,0,sizeof(d)),tot=0;}
void operator +=(ll x){
for(int i=62;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x,tot++;break;}
}
}
ll& operator [](int x){
return d[x];
}
void operator +=(lb &x){
for(int i=62;i>=0;i--)if(x[i])*this+=x[i];
}
friend lb operator +(lb &x,lb &y){
lb z=x;
for(int i=62;i>=0;i--)if(y[i])z+=y[i];
return z;
}
int calc(){//calculate the number of possible xor values, from the vector v
ll tmp=0;
int ret=0,sz=v.size();
for(int i=62;i>=0;i--)if(d[i])tmp|=d[i];
for(int i=62;i>=0;i--){
int cnt=0;
for(ll j:v)cnt+=((j>>i)&1);
if(tmp&(1ll<<i))(ret+=((1ll<<i)%mod)*((1ll<<(tot-1))%mod)%mod*((1ll*sz*(sz-1)/2)%mod)%mod)%=mod;
else(ret+=((1ll<<i)%mod)*((1ll<<tot)%mod)%mod*(1ll*cnt*(sz-cnt)%mod)%mod)%=mod;
}
return ret;
}
}LB;
struct node{
int to,next;
ll val;
}edge[400100];
void ae(int u,int v,ll w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
bool vis[100100];
void dfs(int x){
vis[x]=true,v.push_back(dis[x]);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!vis[edge[i].to])dis[edge[i].to]=dis[x]^edge[i].val,dfs(edge[i].to);
else LB+=dis[x]^dis[edge[i].to]^edge[i].val;
}
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head));
for(ll i=1,x,y,z;i<=m;i++)scanf("%lld%lld%lld",&x,&y,&z),ae(x,y,z);
for(int i=1;i<=n;i++)if(!vis[i])dfs(i),(res+=LB.calc())%=mod,LB.clear(),v.clear();
printf("%d\n",res);
return 0;
}
II.【清华集训2014】玛里苟斯
当k=1的情况之前已经说过,总和是(\bigvee\limits_{d_i\neq 0}d_i)\times 2^{tot-1}。如果我们设\bigvee\limits_{d_i\neq 0}d_i=tmp的话,则是tmp\times 2^{tot-1}。然后现在因为是求期望,因此除以2^{tot}即可。则最终结果为\dfrac{tmp}{2}。
因为答案在2^{64}以内,所以tmp直接用unsigned long long存一下,然后最后一位特判到底是无小数还是输出.5即可。
此部分代码:
void calc1(){
if(tmp&1)printf("%llu.5\n",tmp>>1);
else printf("%llu\n",tmp>>1);
}
当k=2时,我们设tmp的第i位为b_i。则每一位上都有\dfrac{2^{tot-1}}{2^{tot}}=1/2的概率出现一个1,则总和即为\sum\limits_{i=0}^{63}b_i\times2^{i}\times (1/2)。但是我们还要平个方,于是便得到了(\sum\limits_{i=0}^{63}b_i\times2^{i-1})^2。
暴力拆开,我们要求的东西就是\sum\limits_{i=0}^{63}\sum\limits_{j=0}^{63}b_ib_j2^{i+j-2}。
则显然,只有b_i与b_j都为1的地方才能贡献出2^{i+j-2}。
但是这里又有一种情况,就是在所有a_i(即原数组)中,总有第i位同第j位相等。这就意味着第i位与第j位绑定了,它们总是相同。如果绑定了,这两者因为始终相等,概率就不是两个1/2乘在一起,而是直接一个1/2了!
我们设是否绑定为一个bool值sm来表示,如果为true就是绑定上了。则最终答案即为\sum\limits_{i=0}^{63}\sum\limits_{j=0}^{63}b_ib_j2^{i+j-2+sm}。
等等,那输出怎么办?它要求输出精确值呀!
没关系!当i+j\geq2时,结果肯定是整数;
当i+j=1时,末尾是0或0.5;
当i+j=0时,有且只有i=j=0才会出现这种情况,而此时因为i=j,所以肯定就绑定上了!因此它最终是b_0\times b_0\times2^{-1},结尾仍是0或0.5。
所以最终结尾仍是0或0.5。
但是这又有问题了——它只保证结果小于2^{63},但是没有保证中间结果小于2^{63}!
我们要么用double储存,要么用__int128,要么也可以用两个unsigned long long拼一起模拟__int128。
这里采取两个ull拼一起的方法。
此部分代码:
void calc2(){
for(int i=0;i<32;i++)for(int j=0;j<32;j++){
if(!(tmp&(1ull<<i)))continue;
if(!(tmp&(1ull<<j)))continue;
bool sm=true;
for(int p=1;p<=n;p++)if(((a[p]>>i)&1)!=((a[p]>>j)&1)){sm=false;break;}
if(i+j-2+sm<0)floa++;
else inte+=(1ull<<(i+j-2+sm));
}
inte+=(floa>>1),floa&=1;
if(floa)printf("%llu.5\n",inte);
else printf("%llu\n",inte);
}
当k\geq 3时,因为答案小于2^{63},你开一个3次根,结果肯定小于2^{22}。所以直接暴力枚举2^{22}种线性基的子集即可通过。当然,这里仍得使用两个ull进行拼接。
此部分代码:
void calc3(){
for(int i=0;i<64;i++)if(d[i])arr[tot++]=i;
for(ll i=0;i<(1llu<<tot);i++){
ll s=0;
for(int j=0;j<tot;j++)if(i&(1llu<<j))s^=d[arr[j]];
ll p=0,q=1;
for(int l=0;l<k;l++)p*=s,q*=s,p+=(q>>tot),q&=(1llu<<tot)-1;
inte+=p,floa+=q;
inte+=(floa>>tot),floa&=(1llu<<tot)-1;
}
if(floa)printf("%llu.5\n",inte);
else printf("%llu\n",inte);
}
Part6.线性基区间修改
有的时候,我们会遇到这样的题,要你支持两种操作:
- 区间异或上某数
- 求区间上线性基的某种应用(即上文中介绍的线性基的诸多用法之一)
这时应该如何处理呢?
I.[Ynoi2013]无力回天NOI2017
这里就是例子之一,区间异或+区间最大异或和。
考虑到线性基只具有可加性,并不具有可修改性;故我们不能直接上线段树套线性基。
我们考虑对序列作差分——考虑令一个b_i=a_i\operatorname{xor}a_{i+1}。此时,区间修改在差分数组上就只需要修改一头一尾的值。
而如果要求区间的线性基的话,我们只需要求出差分数组的线性基,然后再加入区间末尾的一个数即可。可以发现此种线性基就等价于原本的线性基(因为线性基是异或等价的)。
于是我们只需要使用两棵线段树,一棵维护差分数组的线性基,复杂度O(n\log^2n);一棵维护原序列的元素(因为我们最终是要加入区间末尾的那个数的),复杂度O(n\log n)。
代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,a[50100];
struct lb{//linear basis?
int d[32];
void print(){
for(int i=0;i<=29;i++)if(d[i])printf("%d:%lld\n",i,d[i]);
}
lb(){memset(d,0,sizeof(d));}
void operator +=(int x){
for(int i=29;i>=0;i--){
if(!(x&(1ll<<i)))continue;
if(d[i])x^=d[i];
else{d[i]=x;break;}
}
}
int& operator [](int x){
return d[x];
}
void operator +=(lb &x){
for(int i=29;i>=0;i--)if(x[i])*this+=x[i];
}
friend lb operator +(lb x,lb y){
lb z=x;
for(int i=29;i>=0;i--)if(y[i])z+=y[i];
return z;
}
int num(){for(int i=29;i>=0;i--)if(d[i])return d[i];return 0;}
int calc(int ip=0){
for(int i=29;i>=0;i--)if((ip^d[i])>ip)ip^=d[i];
return ip;
}
};
#define lson x<<1
#define rson x<<1|1
#define mid ((l+r)>>1)
namespace AES{//adjecent elements' segtree
lb seg[200100];
void build(int x,int l,int r){
if(r-l==1){seg[x]+=a[l]^a[r];return;}
build(lson,l,mid),build(rson,mid,r),seg[x]=seg[lson]+seg[rson];
}
void modify(int x,int l,int r,int P,int val){
if(l>P||r<=P)return;
if(r-l==1){val^=seg[x].num();seg[x]=lb();seg[x]+=val;return;}
modify(lson,l,mid,P,val),modify(rson,mid,r,P,val),seg[x]=seg[lson]+seg[rson];
}
lb query(int x,int l,int r,int L,int R){
if(L<=l&&r<=R)return seg[x];
if(mid>=R)return query(lson,l,mid,L,R);
if(mid<=L)return query(rson,mid,r,L,R);
return query(lson,l,mid,L,R)+query(rson,mid,r,L,R);
}
}
namespace OSS{//original sequence's segtree
int seg[200100];
void pushdown(int x){seg[lson]^=seg[x],seg[rson]^=seg[x],seg[x]=0;}
void build(int x,int l,int r){
if(l==r){seg[x]=a[l];return;}
build(lson,l,mid),build(rson,mid+1,r);
}
void modify(int x,int l,int r,int L,int R,int val){
if(l>R||r<L)return;
if(L<=l&&r<=R){seg[x]^=val;return;}
pushdown(x),modify(lson,l,mid,L,R,val),modify(rson,mid+1,r,L,R,val);
}
int query(int x,int l,int r,int P){
if(l==r)return seg[x];
pushdown(x);
return P<=mid?query(lson,l,mid,P):query(rson,mid+1,r,P);
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
if(n!=1)AES::build(1,1,n);OSS::build(1,1,n);
for(int i=1,a,b,c,d;i<=m;i++){
scanf("%d",&a),scanf("%d%d%d",&b,&c,&d);
if(a==1){
OSS::modify(1,1,n,b,c,d);
AES::modify(1,1,n,b-1,d);
AES::modify(1,1,n,c,d);
}else{
lb res;
if(b!=c)res=AES::query(1,1,n,b,c);
res+=OSS::query(1,1,n,c);
printf("%d\n",res.calc(d));
}
}
return 0;
}
II.CF587E Duff as a Queen
和上题几乎一致,可以被看作是双倍经验,代码就不贴了。
INF.总结
线性基是一种很奇妙的东西,在求关于异或的东西的时候非常实用。同时,要注意它要与其它一些可以使用异或的数据结构区分,如01trie等。
它主要的用途有:
- 最大/最小/k大异或和
- 异或和数量
- 异或和的和
同时又可以找到“子集”“子序列”等字眼,或者是图论中的某条路径的异或和时,就可以往线性基方向想了。
希望我的讲解能带你们听懂线性基。
参考材料:
a_forever_dream的博客
yangsongyi的博客
sengxian的博客