高中数学 学习笔记
chlchl
·
·
学习·文化课
虽然说洛谷是一个 OI 社区网站,但是嘛,信息数学不分家,况且秉持着一个地方存下所有学习资料的习惯,加上还有 \LaTeX 的辅助,还是写一写吧。
注意:可能掺杂着一些 OI 的内容。如果没有学过 OI,请直接跳过相关部分。
本文持续更新,请想学东西的同学们持续关注,谢谢!
本文仅整理知识点、做题方法及少量例题,更多练习请购买相关教材。
Part 1:集合
几个定义:
- 研究的对象称为元素;
- 元素的总体称为集合。注意:集合不一定要是数字,它里面的元素可以为任意的东西,比如“广州”“和平精英”“Apple”等都是可以放在集合中的。
- 若 A 为有限集(即集合中的元素个数是有限的),集合内元素的个数称为集合 A 的模,写作 |A|。若 |A|=0,则称 A 为空集,记作 \varnothing。
集合的表示:
- 集合用大写字母 A,B,C,\cdots 表示,元素用小写字母 a,b,c,\cdots 表示(可以用 \alpha,\beta 等希腊字母)。
- 集合的表述方式:
- 列举法,如 A=\{1,3,\text{蒟蒻},5,10,\text{IAKIOI}\}。
- 描述法,如 A=\{x|x^2+2x-3=0,x\neq3\}。这种描述方式的格式是在最前面写上变量名(x),打一个竖杠,后面写 x 需要满足的条件(只有满足所有条件才归属于集合中)。比如上述集合表示的就是满足方程 x^2+2x-3=0 且 x\neq 3 的所有实数 x。
例子:B=\{1,3,2,0,24\},C=\{(x,y)|xy<0,x+y\leq 9\}。
常用的集合字母及其所对应的意义:实数集 \mathbb{R}、整数集 \mathbb{Z}、有理数集 \mathbb{Q}、自然数集 \mathbb{N}。对于任意一个常用集合字母,在它上面打上 号意味着排除 0,打上 + 意味着仅是正数。如 \mathbb{R_+} 表示的是正实数集、$\mathbb{N^} 表示的是除 0$ 外的自然数集,即正整数集。
元素与集合的关系:
- 如果一个元素 x 在集合 A 中,则称 x 属于 A,记作 x\in A。
- 反之则称 x 不属于 A,记作 x\notin A。
集合与集合的关系:
- 包含:如果 A 中任意一个元素都是 B 中的元素,则称 A 为 B 的子集,写作 A\subseteq B 或 B\supseteq A,读作 A 包含于 B 或 B 包含 A。
- 如果 A\subseteq B 且 B 中至少有一个元素在 A 中没有出现,称 A 为 B 的真子集,写作 A\subset B 或 B\supset A(有的教科书上用 \subset 表示包含,用 \varsubsetneqq 表示真包含)。
- 相等:如果 A 与 B 中的元素一一对应,则 A=B。当然,若 A\subseteq B,B\subseteq A,则 A=B。
特别地,空集的关系要提一下。
-
-
集合三要素:
- 确定性。对于任意一个元素,是否存在于集合中是确定的。即不能即在集合中,又不在集合中。
- 无序性:元素是无序的,即 \{1,2,3\} 和 \{3,2,1\} 是同一个集合。但是在 OI 中,我们有有序集,比如 STL 中的
set。
- 互异性:集合中的元素互不相同。但是在 OI 中,我们的
multiset 是可重复集。
全称量词与存在量词:
- 若集合 A 中每一个元素 x 都满足 p(x) 这个条件,可以用 \forall 表示。例:\forall x\in A,x>1,意思就是集合 A 中的任意一个元素 x 都满足 x>1。
- 若集合 A 中有某个元素 x 满足 p(x) 这个条件,可以用 \exists 表示。例:\exists x\in A,x>1,意思是集合 A 中有某个元素 x 大于 1。
- 命题的否定:
- 全称量词命题 \forall x\in A,p(x) 的否定:\exists x\in A,\neg p(x)(\neg 是非的意思,即不满足条件)。
- 存在量词命题 \forall x\in A,p(x) 的否定:\forall x\in A,\neg p(x)。
- 讲人话,如果有一个 x 不满足 p(x),那就不是所有 x 都满足;如果所有 x 都不满足 p(x),那就没有一个 x 满足。
集合的运算:
- 交集:既出现在集合 A,又出现在集合 B 中的元素,称为 A,B 的交集,记作 A\cap B,读作 A 交 B。在 OI 中有一个逻辑符号跟它长得很像,那就是与运算 \land。
- 并集:出现在集合 A 或出现在集合 B 中的元素,称为 A,B 的并集,记作 A\cup B,读作 A 并 B。在 OI 中也有一个逻辑符号跟它长得很像,那就是或运算 \lor。
- 补集:设集合 A 为全集 U 中的一个子集。\forall x\in U,x\notin A 所构成的集合称为 A 的补集,记作 C_UA。在不引起误会时也可以记为 \overline{A}。在 OI 中也有一个逻辑符号跟它长得不是很像,那就是非运算 !。
一个图解释一下集合的运算:
运算定律:
-
-
- 德摩根(\text{De Morgen})定律:C_U(A\cup B)=C_UA\cap C_UB,\quad C_U(A\cap B)=C_UA\cup C_UB。
Part 2:二次函数、方程、不等式
二次方程的解与二次函数图像的关系:形如 ax^2+bx+c=0(a\neq 0) 的方程的解可以转化为二次函数 y=ax^2+bx+c 与 x 轴的交点(y=0 的时候)。
解的情况如下:
当然,一元二次不等式的解也和二次函数相关。
- 若 ax^2+bx+c\leq m,且方程 ax^2+bx+c-m=0 有解,则解集在方程的两根之间。
- 若 ax^2+bx+c\geq m,且方程 ax^2+bx+c-m=0 有解,则解集在方程的两根之外。
设方程 ax^2+bx+c-m=0 的两根为 x_1,x_2(x_1\leq x_2),图示:
该方法可以扩展到高次不等式中。设 x_1<x_2<\cdots<x_k,现有不等式 (x-x_1)(x-x_2)\cdots(x-x_k)\geq 0,我们大概画出其 y=(x-x_1)(x-x_2)\cdots(x-x_k) 的图像(多次函数的图像不展开说明,比较基础),找到其大于 0 的部分即可。这个方法也叫“穿针引线”。
Part 3:函数的基本概念、性质
函数基本概念
函数的定义:设 A,B 为非空数集。若 \forall x\in A,都有唯一的 f(x)\in B 与之对应,则称 f:A\rightarrow B 为从 A 到 B 的函数,记作 y=f(x),x\in A,其中 x 为自变量。
函数 f 只是一个符号,可以用其他符号代替,例如 y=g(x)。
函数三要素:
- 定义域:自变量取值的范围。
- 对应法则:两个变量之间的对应关系,你可以简单理解为解析式,如 y=x^2+2x。
- 值域:所有函数值构成的集合。
以 y=f(x),x\in A 为例,它的定义域是 A,对应法则是 f(x),值域是 \{y|y=f(x),x\in A\}。
相同函数的判定:当两个函数的定义域与对应法则都相同时,它们是相同函数(因为值域肯定也相同)。
一定注意了,因为 y=x 和 y=\frac{x^2}{x} 不是相同函数,因为定义域不一样。
区间的几何表示
函数的定义域与值域通常用区间表示。
-
-
-
-
含有无穷的区间表示:
-
-
-
-
求定义域
相对来说这个比较简单,注意下面的东西即可:
- 分母不为 0;
- 偶次根号不为负;
-
-
- 其他初等函数的定义域要求等等。
有几个东西就列几个方程 / 不等式即可。
这里有个非常坑的地方:比如求 f(x+1)=\sqrt x 的定义域。这与求 f(x)=\sqrt x 的定义域是不一样的,因为定义域指的是 x 的取值范围,而不是括号内的取值范围。
我们必须把 f(x+1)=\cdots 变成 f(x)=\cdots 才能正常地解出解析式。
将 t=x+1 带入,得 f(t)=\sqrt{t-1}。这个的定义域是 [1,+\infty],所以 f(x) 的定义域也是 [1,+\infty]。
求法则
有四种方案。
注意,法则求出来之后记得分析定义域。记得分析定义域。记得分析定义域。记得分析定义域。记得分析定义域。记得分析定义域。记得分析定义域。记得分析定义域。
1、换元
这是最基础、最万能的一种。
比如求 f(4x+1)=\dfrac{1}{3x-1} 的法则。
令 t=4x+1,则 x=\dfrac{t-1}{4}。带入式子,得到 f(t)=\dfrac{1}{3\times\frac{t-1}{4}-1}=\dfrac{4}{3x-7}。
2、拼凑
这个方法非常无聊。
比如求 f\big(2x+\dfrac{1}{x}\big)=4x^2+\dfrac{1}{x^2}-4。这个式子可以直接看出来,因为 4x^2+\dfrac{1}{x^2}-4=(2x+\dfrac{1}{x})^2-8,所以 f(x)=x^2-8。
这种题是非常少的……
3、联立方程
已知 f(x)+2f(-x)=3x-1,求 f(x)。
注意到 x 和 -x 互为相反数,我们将 x'=-x 带进方程中,得到 f(-x)+2f(x)=-3x-1。
这样我们得到了关于 f(x) 和 f(-x) 的方程组,就可以解出 f(x) 了。
解得 f(x)=-3x-\dfrac{1}{3}。
4、待定系数
告诉你 f(x) 的形式(比如一次函数、二次函数等),你就可以直接设,然后根据题目的信息求,贼简单,初中题。
已知一次函数 f(x) 满足 3f(x+1)-2f(x-1)=2x+17。求 f(x) 解析式。
设 f(x)=kx+b,则有 3[k(x+1)+b]-2[k(x-1)+b]=2x+17。
化简,得 kx+5k+b=2x+17。
所以 \begin{cases}
k=2\\
5k+b=17\\
\end{cases},解得 k=2,b=7。所以 f(x)=2x+7。
求值域
还是先分析好定义域,先分析好定义域,先分析好定义域,先分析好定义域,先分析好定义域,先分析好定义域,先分析好定义域,先分析好定义域。
然后就没啥好说的了,一般就是看看根号、基本函数(二次函数、对勾函数比较多)、分母那些东西,看看有什么可以求的,基本没啥套路。
来道难一点的:求 f(x)=\sqrt{3x-1}+\sqrt{2-3x} 的值域。
首先分析定义域:x\in[\dfrac{1}{3},\dfrac{2}{3}]。接下来有两种方法。
sol 1
两个分开的根号不好玩,把它合起来。
f^2(x)=3x-1+2-3x+2+2\sqrt{(3x-1)(2-3x)}
f^2(x)=1+\sqrt{-9x^2+9x-2}
因为 -9x^2+9x-2\in[0,\dfrac{1}{4}](注意 x 的定义域),
所以 f^2(x)\in[1,2],得到 f(x)=[1,\sqrt2]。
sol 2
极强的数感告诉我们,(\sqrt{3x-1})^2+(\sqrt{2-3x})^2=1,想到 \sin^2+\cos^2=1。
令 \sqrt{3x-1}=\sin a,\sqrt{2-3x}=\cos a,f(x)=\sin a+\cos a。
这样没法分析,我们还是想办法给它合在一起。
注意到 \sin45\degree=\cos45\degree=\dfrac{\sqrt2}{2},所以考虑提取这个东西出来,得到:
f(x)=\sqrt2(\sin a\cdot\dfrac{\sqrt 2}{2}+\cos a\cdot\dfrac{\sqrt 2}{2})
稍微化简,得到
f(x)=\sqrt2(\sin a\cos45\degree+\cos a\sin45\degree)
结合后面学的和差角公式,得到:
f(x)=\sqrt2\sin(a+45\degree)
## 函数的性质
### 1、单调性
### 2、奇偶性
### 3、周期性
### 4、凹凸性(不太常见)
# 基本初等函数
## 1、对勾函数
形如 $y=ax+\frac{b}{x}$ 的函数被称为对勾函数。
对勾函数的图像大概长这样,因为形似对勾,因此得名:
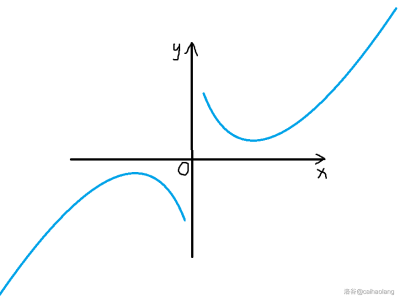
它的顶点为 $\pm2\sqrt{ab}$,用均值不等式证的,读者自证不难。
应用就是求一些形如 $ax+\frac{b}{x}$ 的东西的值域,往下走就知道了。
## 2、指数函数
## 3、对数函数
## 4、幂函数
## 5、三角函数
### 弧度制
> 前面一大堆东西咕了
### 诱导公式
> 前面一大堆东西咕了
### 和差角公式
这是一个非常重要的结论。不过,我们以一个铺垫入手:余弦定理。
#### 余弦定理
现有一个三角形 $ABC$,其三边分别为 $a,b,c$。过 $B$ 作 $BD\bot AC$ 交 $AC$ 于 $D$。如图所示。
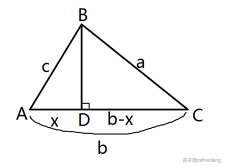。
设 $BD=x,CD=b-x$。由勾股定理得 $c^2-x^2=a^2-(b-x)^2$。解得 $x=\dfrac{b^2+c^2-a^2}{2b}$。
由此,我们得到了角 $A$ 的余弦值:$\cos A=\frac{x}{AB}=\dfrac{b^2+c^2-a^2}{2bc}$。
同理,在其他两条边作高,我们可以得到剩下两个角的余弦值。
$\cos B=\dfrac{a^2+c^2-b^2}{2ac},\cos C=\dfrac{a^2+b^2-c^2}{2ab}$。
这三个角的余弦值,就称为**余弦定理**。
有了余弦定理,我们可以在平面直角坐标系内继续整活。
画出单位圆,并随便画两条从原点出发的射线,角度分别为 $\alpha,\beta$,分别交单位圆与 $A,B$ 两点,连接 $AB$。如图所示。

可以看到两条边的夹角就是 $\alpha-\beta$。现在我们看看有什么已知信息:$A(\cos\alpha,\sin\alpha),B(\cos\beta,\sin\beta),OA=OB=1$。
够了,根据余弦定理,可以轻松求出 $\cos(\alpha-\beta)=\dfrac{OA^2+OB^2-AB^2}{2\times OA\times OB}=\dfrac{1+1-(\cos\alpha-\cos\beta)^2+(\sin\alpha-\sin\beta)^2}{2}=\cos\alpha\cos\beta+\sin\alpha\sin\beta$。
那 $\cos(\alpha+\beta)=\cos(\alpha-(-\beta))=\cos\alpha\cos\beta - \sin\alpha\sin\beta$。
剩下还有 $4$ 条式子,一共 $6$ 条,我一起列在下面,推的原理差不多,$\tan$ 直接用 $\dfrac{\sin}{\cos}$ 求即可。
- $\sin(\alpha+\beta)=\sin\alpha\cos\beta + \cos\alpha\sin\beta$。
- $\sin(\alpha-\beta)=\sin\alpha\cos\beta - \cos\alpha\sin\beta$。
- $\cos(\alpha+\beta)=\cos\alpha\cos\beta - \sin\alpha\sin\beta$。
- $\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$。
- $\tan(\alpha+\beta)=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}$。
- $\tan(\alpha+\beta)=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}$。
### 两(三)倍角公式
有了和差角公式,二倍角公式就很简单了。不过它仍然是一个重点。
$\sin2\alpha=\sin(\alpha+\alpha)=2\sin\alpha\cos\alpha$。
同理可得以下两个公式:
- $\cos2\alpha=\cos^2\alpha-\sin^2\alpha=2\cos^2\alpha-1=1-2\sin^2\alpha$。
- $\tan2\alpha=\dfrac{2\tan\alpha}{1-\tan^2\alpha}$。
这几个公式很有潜力,可以衍生出很多变形。
1. 借助完全平方公式:$(\sin\alpha\pm \cos\alpha)^2=1\pm \sin2\alpha$。
2. 结合和差角公式,可以推出三个**万能公式**:
- $\sin\alpha=\dfrac{2\tan\frac{\alpha}{2}}{1+\tan^2\frac{\alpha}{2}}$。
- $\cos\alpha=\dfrac{1-\tan^2\frac{\alpha}{2}}{1+\tan^2\frac{\alpha}{2}}$。
- $\tan\alpha=\dfrac{2\tan\frac{\alpha}{2}}{1-\tan^2\frac{\alpha}{2}}$。
3. 三倍角公式(竞赛内容,高考路线可跳过)。
- $\sin 3\alpha=3\sin\alpha-4\sin^3\alpha=4\sin\alpha\sin(60^\circ-\alpha)\sin(60^\circ+\alpha)$。
- $\cos 3\alpha=4\cos^3\alpha-3\cos\alpha=4\cos\alpha\cos(60^\circ+\alpha)\sin(60^\circ-\alpha)$。
- $\tan 3\alpha=\dfrac{3\tan\alpha-\tan^3\alpha}{1-3\tan^2\alpha}=\tan\alpha\tan(60^\circ-\alpha)\tan(60^\circ+\alpha)$。
具体怎么推的我也忘了,自己上网找教程吧(~~本蒟蒻并不是高联方向~~)。
### 辅助角公式
这个公式其实挺无聊的,通常运用在化简等纯代数运算中。有时也用来合并相同大小的角。
这个定理掺和了一点勾股定理:
$m\sin\alpha+n\cos\alpha=\sqrt{m^2+n^2}(\dfrac{m}{\sqrt{m^2+n^2}}\sin\alpha+\dfrac{n}{\sqrt{m^2+n^2}}\cos\alpha)
这个 $\beta$ 是我们自己引入的值,如果实在求不出来具体的 $\beta$ 可以直接写这个字母,因为你给出了 $\sin\beta$ 和 $\cos\beta$,足以把 $\beta$ 求出来,只不过不想算而已。
### 和差化积与积化和差
这也是一个重点。这个结论仍然使用和差角公式推导。
#### 和差化积
以 $\sin\alpha+\sin\beta$ 为例。
$\because\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta,
$\therefore \sin(\alpha+\beta)+\sin(\alpha-\beta)=\sin\alpha\cos\beta$。
$\therefore 2\sin\alpha\cos\beta=\sin(\alpha+\beta)+\sin(\alpha-\beta)$。
然后接下来我们进行还原,用 $\alpha$ 表示原来的 $\alpha+\beta$,用 $\beta$ 表示原来的 $\alpha-\beta$,再把 $2$,式子变成:$\sin\alpha+\sin\beta=2\sin\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha-\beta}{2}$。
剩下几个式子是相似的,所以我们得到了 $4$ 个式子(没有 $\tan$)。
- $\sin\alpha+\sin\beta=2\sin\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha-\beta}{2}$。
- $\sin\alpha-\sin\beta=2\sin\dfrac{\alpha-\beta}{2}\cos\dfrac{\alpha+\beta}{2}$。
- $\cos\alpha+\cos\beta=2\cos\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha-\beta}{2}$。
- $\cos\alpha-\cos\beta=-2\sin\dfrac{\alpha+\beta}{2}\sin\dfrac{\alpha-\beta}{2}$。
#### 积化和差
这个直接用和差角公式拆开就可以得到。
- $\sin(\alpha+\beta)+\sin(\alpha-\beta)=2\sin\alpha\cos\beta$。
- $\sin(\alpha+\beta)-\sin(\alpha-\beta)=2\cos\alpha\sin\beta$。
- $\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta$。
- $\cos(\alpha-\beta)-\cos(\alpha+\beta)=2\sin\alpha\sin\beta$。
**注意最后一条式子的顺序**。