van Emde Boas树 手把手入门
2018heyuyang
·
·
个人记录
前言
这篇博客是是面向初学者(或者感兴趣的同学)而写的,因为网上的文章对于我这样的naive实在是太不友好了,现在终于搞懂了,就写一篇通俗易懂的发出来
但是在学这玩意前,至少需要掌握 线段树 和 分块 等 分治数据结构 的初步应用,也许还要会敲 普通平衡树 这个板子
-1.van Emde Boas树的介绍
van Emde Boas树,简称vEB树(但是我喜欢把它叫作van树)
它可以做到O(n\times loglogn)解决下面的问题
维护一个数据结构,有n次操作,操作有4种
$2.$删除一个数$x$(若$x$不存在,则不操作)
$3.$查询$x$的前驱(前驱为“小于$x$的数中,最大的那个数的值”)
$4.$查询$x$的后继(后继为“大于$x$的数中,最小的那个数的值”)
## 0.复合函数loglogn
先来感受下$loglogn$有多小
当$k=loglogn$时,$n=2^{2^k}$,代入$k=5$,得$n
=2^{32}
也就是说loglogn在一般数据范围里可看作一个小常数(总之非常快)
就是一个数不断对自己开方(向下取整),开方多少次能够变成1,这个次数就是$loglogn$的值(证明其实真不难)
我们的van树也是根据这个性质建造的
## 1.van树长什么样
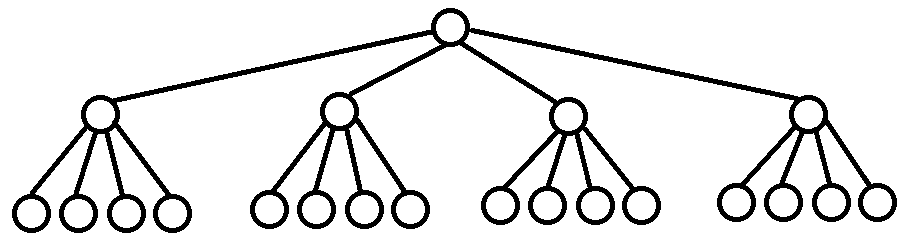
这是一颗“分块树”,每个非叶子节点都有$\sqrt n$个子节点,其实这玩意和分块几乎没有区别,同样是只分治一次
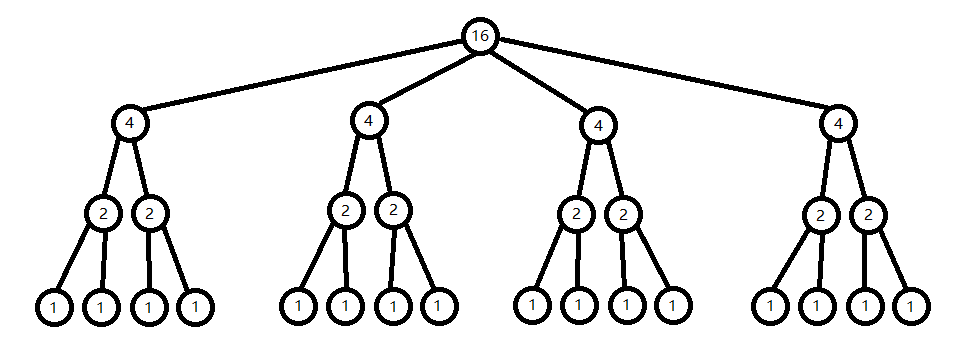
那么van树便是上面这样的**分块无限套娃**,**每一个规模为$u$的节点按照$\sqrt u$来继续分治,直到$u<=2$**
实际上,上图最底层那一排$1$是可以不要的,因为规模$<=2$时已经可以直接特判了
显然树高为$loglogn
这里提醒一点,van树是按值域来分治的
2.van树储存了什么信息
van树的每一个节点都是一个结构体,下面给出一张图(资料上就长这样)(该节点的对应区间为0~15)
结合一下平衡树模版你就可以知道,min,max是区间内,那些存在的数字,的最值
儿子节点就是一个分治,再次提醒:按\sqrt u的大小分治,儿子节点有\sqrt u个
还有一个我把它叫做“浓缩”节点(资料上是summary)
总结一下几个要点:“分块套娃”、“每个规模为u的节点有\sqrt u个子节点和一个额外的浓缩节点”
上面只是讲里面有什么变量,下面讲用处
下面定义bool数组a,若a[i]=0则i这个数字不存在;若a[i]=1则i这个数字存在。
#include<cstdio>
using namespace std;
bool a[65536];
void ins(int x){a[x]=1;}
void del(int x){a[x]=0;}
int findqianqu(int x)
{
for(int i=x-1;i>=0;i--)if(a[i])return i;
return -1;
}
int findhouji(int x)
{
for(int i=x+1;i<65536;i++)if(a[i])return i;
return -1;
}
int A(int l,int r)
{
for(int i=l;i<=r;i++)if(a[i])return 1;
return 0;
}
int main()
{
return 0;
}
这个代码改一改就可以变成原题的暴力了
注意下我打了个A函数进去,等下我要用……
原问题变成这样:维护a数组
每个位置(如a[0],a[5],a[233],a[6666])为0或1表示数字是否存在,其余操作的暴力版都在代码里了
接下来讲结构体中变量的意义
我们先把数据的值域定为[0,65535],因为这样方便开根
那么根节点的规模u就是65536啦,把该节点读作节点p
$p$的$min$和$max$挺好理解的,$min$就是顺数第一个$1$的位置,$max$就是倒数第一个$1$的位置
我们设$p$掌管的区间为$[l,r]$,$min$、$max$的结果就是下面的sb代码(特别的,不存在就返回$-1$)
```cpp
int min(int l,int r)
{
for(int i=l;i<=r;i++)if(a[i])return i;
return -1;
}
int max(int l,int r)
{
for(int i=r;i>=l;i--)if(a[i])return i;
return -1;
}
```
$p$有$\sqrt u$个儿子,他们把$p$的$[l,r]$给分块掉了
就比如根节点$p$的区间为$[0,65535]$,有$256$个儿子,它的$0$号儿子管理区间$[0,255]$,$1$号儿子管理区间$[256,511]$,以此类推
儿子的$min$,$max$求法和$p$一样,但要注意,是从**管理区间**里面求
可以发现,根节点对于区间$[0,65535]$,只记录了两个值,除掉直接特判的情况,下面还有一堆儿子,$well$,$hou$ $can$ $you$ 在茫茫人海中快速 $find$ 前驱/后继?
下面就给你讲
## 3.van树查找后继(1)
我们现在要查询x的后继,函数返回一个整数或者是$-1
首先我们判断是否有解
1.看看van树是否为空,只要看一下根节点(root节点)的min和max是否为-1
2.排除1情况后,van树的max就一定有值,这里检查x是否>=root.max,是的话就无解
3.到了这里,你知道了解是存在的,再次进行分类讨论:
若x<root.min,直接返回root.min
若root.min<=x<root.max
现在我们令p=root
我们这时看一眼 x所对应的 p节点的 儿子节点
若我们的后继出现在这个儿子节点内,我们就可以缩小查找的范围,那么此时有[1]、[2]两种情况
$[2]$ $son.min<=x<son.max$,我们就继续跳到孙子节点,实际上这里一个$while$循环就可以处理,直接让$p=son$就行,然后继续判断$[1]$、$[2]$情况
$[3]$ 如果$son.min$、$son.max$为$-1$ 或者 $x>=son.max$($[3]$情况表示$x$的后继不在这个儿子节点)
来看下图(注意此时$p$节点是一定有解的,而$son$节点是没有解的)
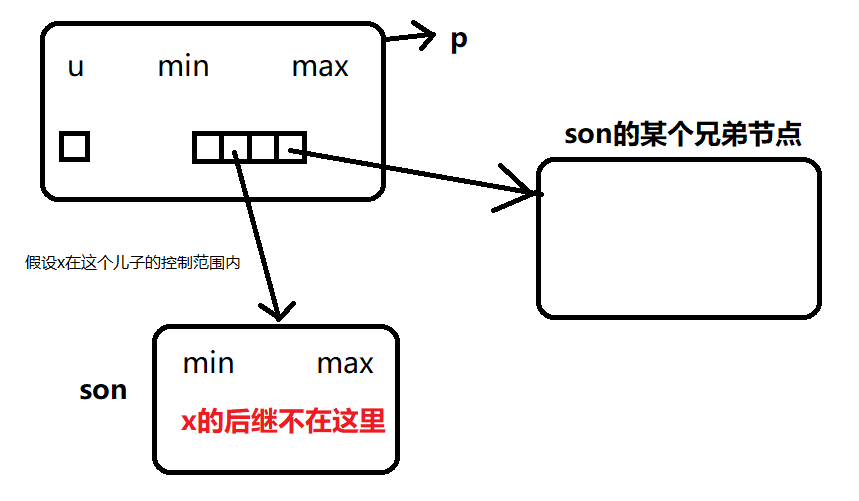
不难得知,解会出现在$son$右手边的某个兄弟节点里,也就是说我们要找的$brother$节点要满足下面的几个条件
$1.$掌管区间内存在$a[i]=1(i\in[l,r])$也就是$A(l,r)=1
只要找到离$son$最近的那个就可以了,然后直接输出 $brother.min$ 问题就能解决
先别管怎么找到$brother$,下面给出一个伪代码
```cpp
int findhouji(int x)
{
int p=root;
if(tr[p].min==-1)return -1;
if(x>=tr[p].max)return -1;
if(x<tr[p].min)return tr[p].min;
while(1)
{
int m=sqrt(tr[p].u);//取块长
int w=x/m;//x在哪个儿子
int son=tr[p].son[w];//取儿子下标
if(tr[son].min!=-1)
{
if(x<tr[son].min)return tr[son].min;
else if(x<tr[son].max){p=son;continue;}
}
int brother=findbrother(p,w);//找到son右手边的brother
return tr[brother].min;
}
}
```
## 4.van树查找后继(2)
我们就差一个$findbrother$函数了
为了高效,我们用同样的分治方式来确定那个$brother
现在讲上面所说的“浓缩”节点,我们还是用summary把(sum和mary连读)
还记得$p$把区间$[0,65535]$分成$256$段吗,也就是$[0,255]$、$[256,511]$……
也就是说,每个儿子对应一个大小为$\sqrt u$的数组($u=65536$)
$summary$和这些$son$极其相似,也对应一个大小为$256$的数组$a'
假设$x$位于$tr[p].son[w]$,我们是不是问一下$a'[w+1,r]$就可以找到$brother$了
对比一下没有$summary$节点我们是怎么做的:把$p$的每个孩子问一遍(查$min$,$max$),$O(\sqrt u)
现在你有了summary,也有了一个a'数组,怎样?for一遍?还是O(\sqrt u)?
no no no
冷静下来你会发现,我们现在要求a'[0~255]中w的后继
还记得我们原来要干什么吗,求a[0~65535]中x的后继
天哪,这还看不出来?你什么时候把规模为u的问题变成\sqrt u的?!
我想到这里你们就可以明白了,这便是一个不断递归缩减规模的过程,于是a'又拆成一堆min,max来维护
我们用O(1)的时间将大小为u的问题变成大小为\sqrt u的问题,递归loglogu层
单次询问复杂度O(loglogn)就是这么来的
5.van树的空间复杂度
S(n)=\sqrt n+\sqrt n\times S(\sqrt n)=n
但是很抱歉,这玩意的n是值域。。。
不过我们的操作次数显然不会太多
适当开下空间就好
6.其它操作?
重申,这篇博客是是面向初学者(或者感兴趣的同学)而写的,篇幅不会很长,抓的也都是重点,注重理解,理解!
其实当你理解summary的作用时,网上的资料也就不难看懂了
这里唯一需要额外提的一个操作就是min,max的“丢失”
因为树的某些链上min,max值都是一样的,所以只用父节点记录而子节点不必记录,但是需要整合信息
这里的代码就咕掉了,网上一堆,咕咕咕qwq
update
当然,作为数据结构爱好者
我还是补上了新的代码(2020.12.19),link