高中数学笔记 - 解析几何
liuhaopeng
·
2024-12-23 20:36:41
·
学习·文化课
数学笔记全文
修订
直线和圆的方程
倾斜角:x 轴正向与直线 l 向上的方向之间所成的角 \alpha 。
斜率:k=\tan\alpha=\frac{y_2-y_1}{x_2-x_1} 。
l_1\perp l_2\implies k_1\cdot k_2=-1,|\alpha_1-\alpha_2|=90\degree
直线的一般式方程:Ax+By+C=0\implies 斜截式方程 y=-\frac{A}{B}x-\frac{C}{B}\implies 该直线的方向向量 \overrightarrow{u}=(B,-A) ,法向量 \overrightarrow{n}=(A,B) 。
点到直线距离公式:\displaystyle \boxed{d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}}
两条平行直线之间距离:\displaystyle \boxed{d=\frac{|C_1-C_2|}{\sqrt{A^2+B^2}}}
两条平行直线之间的铅锤高差:\displaystyle\boxed{h=\frac{|C_1-C_2|}{|B|}}
若 y=kx+b ,则直线上两点间距离 |AB|=\sqrt{1+k^2}|x_1-x_2|=\sqrt{1+\frac{1}{k^2}}|y_1-y_2|
对称问题
点 (x,y) 关于 (a,b) 对称点为 (2a-x,2b-y) 。
直线 l:Ax+By+C=0 关于点 (x_0,y_0) 的对称直线 A(2x_0-x)+B(2y_0-y)+C=0 。
点关于直线的对称点通过设中点来列方程求。
圆
圆的标准方程:(x-a)^2+(y-b)^2=r^2
圆的一般方程:x^2+y^2+Dx+Ey+F=0 ,其中 D^2+E^2-4F>0 ,化为标准形式为 \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \displaystyle\boxed{\left(x+\frac{D}{2}\right)^2+\left(y+\frac{E}{2}\right)^2=\frac{D^2+E^2-4F}{4}}
两圆关系
内含
内切
相交
外切
相离
公切线数
0 1 2 3 4
以 (x_1,y_1),(x_2,y_2) 为直径的两端点的圆的方程:
(x-x_1)(x-x_2)+(y-y_1)(y-y_2)=0
过圆 (x-a)^2+(y-b)^2=r^2 上一点 (x_0,y_0) 的切线方程为
(x-a)(x_0-a)+(y-b)(y_0-b)=r^2
过圆 x^2+y^2+Dx+Ey+F=0\ (D^2+E^2-4F>0) 上一点 (x_0,y_0) 的切线方程为
x_0x+y_0y+\frac{D(x+x_0)}{2}+\frac{E(y+y_0)}{2}+F=0
设点 M(x_0,y_0) 是圆 (x-a)^2+(y-b)^2=r^2 外一点,过点 M 作圆的两条切线,切点分别为 A,B ,则直线 AB 的方程为
(x-a)(x_0-a)+(y-b)(y_0-b)=r^2
经过圆外一点 P(x_0,y_0) 引圆的两条切线,则
圆的方程
切线长公式
(x-a)^2+(y-b)^2=r^2 \sqrt{(x_0-a)^2+(y_0-b)^2-r^2}
x^2+y^2+Dx+Ey+F=0 \\ (D^2+E^2-4F>0) \sqrt{x_0^2+y_0^2+Dx_0+Ey_0+F}
两圆相交时,两圆方程做差得到公共弦所在直线的方程,即
D_1x+E_1y+F_1-(D_2x+E_2y+F_2)=0
参数方程:P(x,y) 满足 \begin{cases}x=a+r\cos\theta \\ y=b+r\sin\theta\end{cases}(r>0) 的轨迹为 (x-a)^2+(y-b)^2=r^2 。
圆锥曲线的方程
椭圆
概念:平面内到两个焦点 F_1,F_2 的距离的和等于常数( 大于 |F_1F_2| )的点的轨迹叫做椭圆。
集合 P=\set{M||MF_1|+|MF_2|=2a},|F_1F_2|=2c
标准方程
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)\\ 焦点在 x 轴上\frac{x^2}{b^2}+\frac{y^2}{a^2}=1(a>b>0)\\ 焦点在 y 轴上
顶点坐标
(\pm a,0),(0,\pm b) (\pm b,0),(0,\pm a)
对称轴
x 轴、y 轴x 轴、y 轴
焦点坐标
(\pm c,0) (0,\pm c)
准线
x=\pm\frac{a^2}{c}
\boxed{c^2=a^2-b^2}$,离心率 $\boxed{e=\frac{c}{a}}\ (0<e<1)
椭圆的面积:$S=\pi ab$( $a,b$ 分别为长半轴、短半轴的长 )。
准线:椭圆上一点 $M(x,y)$ 与顶点 $F(\pm c,0)$ 的距离和它到定直线 $l:x=\pm\frac{a^2}{c}$ 的距离比是常数 $e$( 椭圆的第二定义 )。
椭圆的第三定义:设 $A(-a,0),B(a,0),P(x,y)\in C$,则 $\boxed{k_{AP}\cdot k_{BP}=-\frac{b^2}{a^2}=e^2-1}$。
#### 椭圆焦点三角形的性质
椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 上异于左、右顶点的点 $P(x_0,y_0)$ 与两焦点 $F_1,F_2$ 构成的 $\Delta PF_1F_2$ 叫做焦点三角形。
以下记 $\angle F_1PF_2=\theta$。
1. 周长 $C=2(a+c)$。
2. 面积 $\boxed{S=b^2\tan\frac{\theta}{2}=c|y_0|=\frac{1}{2}|PF_1||PF_2|\sin\theta=r(a+c)}$,$r$ 为焦点三角形的内接圆半径,当 $y_0=b$ 即点 $P$ 的位置为短轴端点时取最大值,且 $\cos\theta\geq 1-2e^2$。
证明:由余弦定理,
$$|F_1F_2|^2=|PF_1|^2+|PF_2|^2-2|PF_1||PF_2|\cos\theta=(|PF_1|+|PF_2|)^2-2(1+\cos\theta)\cdot|PF_1||PF_2|$$
因为 $|PF_1|+|PF_2|=2a,|F_1F_2|=2c$,所以 $|PF_1||PF_2|=\frac{2a^2-2c^2}{1+\cos\theta}=\frac{2b^2}{1+\cos\theta}
又因为 $\frac{\sin\theta}{1+\cos\theta}=\frac{2\sin\frac{\theta}{2}\cos\frac{\theta}{2}}{1+(2\cos^2\frac{\theta}{2}-1)}=\frac{\sin\frac{\theta}{2}}{\cos\frac{\theta}{2}}=\tan\frac{\theta}{2}$
因此 $S=\frac{1}{2}|PF_1||PF_2|\sin\theta=\frac{b^2\sin\theta}{1+\cos\theta}=b^2\tan\frac{\theta}{2}$
|PF_1|\cdot|PF_2|\in (b^2,a^2]
设 \angle PF_1F_2=\alpha,PF_2F_1=\beta ,则 \displaystyle\boxed{e=\frac{\sin(\alpha+\beta)}{\sin\alpha+\sin\beta}}=\frac{\cos\frac{\alpha+\beta}{2}}{\cos\frac{\alpha-\beta}{2}} ( 证明:正弦定理 )。
若焦点三角形内切圆的圆心为 I ,延长 PI 交 F_1F_2 于点 Q ,则
\frac{|PI|}{|IQ|}=\frac{|PF_1|}{|F_1Q|}=\frac{|PF_2|}{|F_2Q|}=\frac{|PF_1|+|PF_2|}{|F_1Q|+|F_2Q|}=\frac{2a}{2c}=\frac{1}{e}
若椭圆上存在点 P 使得 \angle F_1PF_2=\theta ,则 e\in[\sin\frac{\theta}{2},1) 。
椭圆的其它几何性质
通径:过椭圆 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 的焦点作垂直于长轴的直线,该直线被椭圆截得的弦叫做通径,其长度为 \frac{2b^2}{a} 。
若不垂直,则其长度为 |PP_0|=\frac{\frac{2b^2}{a}}{1-e^2\cos^2\theta}\geq \frac{2b^2}{a}
焦半径:设 P(x,y)\in C,F_1(-c,0),F_2(c,0) ,则 |PF_1|=\sqrt{(x+c)^2+b^2\frac{a^2-x^2}{a^2}}=\sqrt{\frac{c^2}{a^2}x^2+2cx+a^2}=|a+ex| ,同理 |PF_2|=a-ex ,因此 \boxed{|PF|=|a\pm ex|} 。
焦点弦( 过焦点的弦 ):设 AB 是过椭圆 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\ (a>b>0) 的右焦点 F 的一条弦,A(x_1,y_1),B(x_2,y_2),AB 的倾斜角为 \theta ,准线 l:x=\frac{a^2}{c} ,则 \boxed{\frac{|AF|}{|BF|}=\frac{1-e\cos\theta}{1+e\cos\theta},|AB|=\frac{2a(1-e^2)}{1-e^2\cos^2\theta}} 。
证明:过 A 作 AA_1\perp AB 于点 A_1 ,则 |AF|=e|AA_1|=e(\frac{a^2}{c}-c-|AF|\cos\theta)\implies|AF|=\frac{b^2}{a+c\cos\theta}
同理 |BF|=\frac{b^2}{a-c\cos\theta} ,代入得证。
注:一条过焦点的直线会有两个一长一短的焦半径,在公式中,长的对应取减号,短的对应取加号;当焦点在 y 轴上,将 \cos\theta 换为 \sin\theta 。
过一个焦点 F 作弦 AB,AF=d_1,BF=d_2 ,则 \displaystyle\frac{1}{d_1}+\frac{1}{d_2}=\frac{2a}{b^2}
弦长公式:设直线 y=kx+m 与椭圆有两个公共点 M(x_1,y_1),N(x_2y_2) ,则弦长公式:
|MN|=\sqrt{(1+k^2)[(x_1+x_2)^2-4x_1x_2]}=\sqrt{(1+\frac{1}{k^2})[(y_1+y_2)^2-4y_1y_2]}
中点弦问题:求直线 AB 与圆锥曲线相交弦的中点 M 和原点的连线 OM 的斜率问题,\\ 有 \boxed{k_{AB}\cdot k_{OM}=-\frac{b^2}{a^2}=e^2-1} ( 若焦点在 y 轴,则 k_{AB}\cdot k_{OM}=-\frac{a^2}{b^2} )
证明:联立 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\ (a>b>0) 与 y=k_{AB}x+m 得
(b^2+a^2k_{AB}^2)x^2+2mk_{AB}a^2x+a^2m^2-a^2b^2=0
所以 x_1+x_2=\frac{-2mk_{AB}a^2}{b^2+a^2k_{AB}^2},M_x=\frac{x_1+x_2}{2}=\frac{-mk_{AB}a^2}{b^2+a^2k_{AB}^2},m=\frac{b^2+a^2k_{AB}^2}{-k_{AB}a^2}M_x
代入 y=k_{AB}x+m 得 y=-\frac{b^2}{k_{AB}a^2}x\implies k_{AB}\cdot k_{OM}=-\frac{b^2}{a^2}
例题:过椭圆 \frac{x^2}{16}+\frac{y^2}{4}=1 内一点 P(3,1) ,且被这点平分的弦所在的直线方程是 ?
方法一:设 A(x_1,y_1),B(x_2,y_2)\implies \frac{x_1^2}{16}+\frac{y_1^2}{4}=1,\frac{x_2^2}{16}+\frac{y_2^2}{4}=1 ,两式相减得 \frac{(x_1+x_2)(x_1-x_2)}{16}+\frac{(y_1+y_2)(y_1-y_2)}{4}=0
P$ 为 $AB$ 中点 $\implies x_1+x_2=6,y_1+y_2=2 \implies k_{AB}=\frac{y_1-y_2}{x_1-x_2}=-\frac{3}{4}
所以直线 AB 的方程是 3x+4y-13=0 。
方法二:设弦为 AB,k_{OP}=\frac{1}{3},k_{AB}=-\frac{b^2}{a^2}\div\frac{1}{3}=-\frac{3}{4} ,后同方法一。
中点弦问题的推广:椭圆上的点 P 与过椭圆中心的弦 AB 的端点的连线 MA,MB 斜率之积为 \boxed{-\frac{b^2}{a^2}=e^2-1}
证明:作中位线 OT ,易证 k_{MA}\cdot k_{MB}=k_{MA}\cdot k_{OT}=-\frac{b^2}{a^2}=e^2-1
蒙日圆:椭圆上两条互相垂直的切线的交点必在一个与椭圆同心的圆 上,且圆的方程为 x^2+y^2=a^2+b^2 。
过蒙日圆上一点 M 做关于椭圆的切线,与椭圆交于 A,B ,D 为椭圆上任意一点,则 \boxed{k_{DA}k_{DB}=e^2-1} 。
椭圆 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 在 (x_0,y_0) 处的切线方程为 \frac{x_0x}{a^2}+\frac{y_0y}{b^2}=1 ,直接设直线 y=kx+m ,算 \Delta 得证。
过椭圆 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 上任意一点 P ( 不是椭圆的顶点 )作椭圆的切线,设切线的斜率为 k_1 ,直线 OP 的斜率为 k_2 ,则 \boxed{k_1k_2=e^2-1} ,双曲线同样成立 。
过原点 O 的直线 l 与椭圆 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 相交于 A,B 两点,P 为椭圆上任意一点,则 k_{PA}k_{PB}=e^2-1 。
过椭圆 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 上的任意一点 P ( 非顶点 )作倾斜角互补的两条直线交椭圆于 A,B 两点,有 k_{AB}k_{OP}=1-e^2 。
如果是焦点在 y 轴上的椭圆或双曲线,则 \boxed{e^2-1\to\frac{1}{e^2-1}} 。
好题
设直线 l:y=x+1 与椭圆 C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 相交于 A,B 两点,与 x 轴相交于左焦点 F ,且 \overrightarrow{AF}=3\overrightarrow{FB} ,则椭圆的离心率 e= ___
答案:\frac{\sqrt{2}}{2}
解析:方法一:由题得 F(-1,0),c=1 ,设 A(x_1,y_1),B(x_2,y_2) ,联立 y=x+1 与椭圆方程 b^2x^2+a^2y^2=a^2b^2 得
(a^2+b^2)y^2-2b^2y+b^2-a^2b^2=0$,显然 $\Delta>0,y_1+y_2=\frac{2b^2}{a^2+b^2},y_1y_2=\frac{b^2-a^2b^2}{a^2+b^2}\ \circledast
由 \overrightarrow{AF}=3\overrightarrow{FB} 得 0-y_1=3(y_2-0) 即 y_1=-3y_2\ \circledcirc
由 \circledast \circledcirc 消去 y_1,y_2 得 -3b^2=(a^2+b^2)(1-a^2)\xRightarrow{a^2-b^2=c^2=1}a^4-3a^2+1=0\implies a=\pm\sqrt{2}\ \text{or}\ \pm 1
取 a=\sqrt{2} ,所以 e=\frac{c}{a}=\frac{\sqrt{2}}{2} 。
方法二:注意上述关于焦点弦的结论,\frac{|AF|}{|BF|}=\frac{1-e\cos\theta}{1+e\cos\theta}=3 ,代入 \cos\theta=\frac{\sqrt{2}}{2} 可得 e=\frac{\sqrt{2}}{2}
已知椭圆 \frac{x^2}{4}+y^2=1 ,直线 l:y=kx+m 满足 m\neq -2k 且与椭圆相交于不同的两点 A,B ,若以线段 AB 为直径的圆始终过点 Q(2,0) ,试判断直线 l 是否过定点?若是,求出该定点的坐标;若不是,请说明理由。
解:设 A(x_1,y_1),B(x_2,y_2) ,联立 \begin{cases}
y=kx+m \\
\frac{x^2}{4}+y^2=1
\end{cases}
得 (1+4k^2)x^2+8kmx+4m^2-4=0,\Delta=16(4k^2-m+1)>0
则 x_1+x_2=\frac{-8km}{1+4k^2},x_1x_2=\frac{4m^2-4}{1+4k^2},y_1y_2=(kx_1+m)(kx_2+m)=k^2x_1x_2+km(x_1+x_2)+m^2=\frac{m^2-4k^2}{1+4k^2}
因为以线段 AB 为直径的圆过点 Q ,所以 \overrightarrow{QB}\cdot\overrightarrow{QA}=0 ,又 \overrightarrow{QB}=(x_2-2,y_2),\overrightarrow{QA}=(x_1-2,y_1)
所以 \overrightarrow{QB}\cdot\overrightarrow{QA}=x_1x_2-2(x_1+x_2)+4+y_1y_2=\frac{(6k+5m)(2k+m)}{1+4k^2}=0
显然 m=-\frac{6}{5}k\implies l:y=kx-\frac{6}{5}k=k(x-\frac{6}{5}) ,恒过定点 (\frac{6}{5},0) 。
( 齐次化 )3. 已知 \frac{x^2}{4}+\frac{y^2}{3}=1 ,是否存在定圆与 MN(OM\perp ON) ( 动直线 )总相切 ?
设 MN:mx+ny=1 ,代入得 3x^2+4y^2-12(mx+ny)^2=0\implies (3-12m^2)x^2+(4-12n^2)y^2-24mnxy=0
化成 (4-12n^2)k^2-24mnk+3-12m^2=0 ,因为 k_1k_2=\frac{3-12m^2}{4-12n^2}=-1 ,因此 m^2+n^2=\frac{7}{12} ,定圆为 x^2+y^2=\frac{12}{7} 。
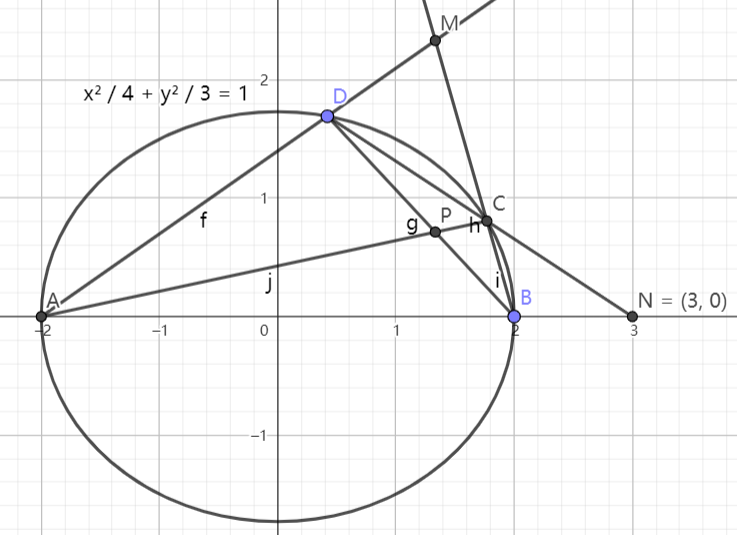
( 定比点差法 )4. 已知 \frac{x^2}{4}+y^2=1,A(-2,0) ,经过 B(1,0) 且斜率存在的直线 l 交椭圆于 P,Q 两点,点 C 与点 P 关于坐标原点对称,连接 AC,AQ ,求 \frac{k_{AC}}{k_{AQ}} 的值。
设 P(x_1,y_1),Q(x_2,y_2),\overrightarrow{PB}=\lambda\overrightarrow{BQ} ,则 x_1+\lambda x_2=1+\lambda,y_1+\lambda y_2=0
\begin{cases} \frac{x_1^2}{4}+y_1^2=1 \\ \frac{x_2^2}{4}+y_2^2=1 \end{cases}\implies \begin{cases} \frac{x_1^2}{4}+y_1^2=1 \\ \frac{\lambda x_2^2}{4}+\lambda y_2^2=\lambda \end{cases}
两式作差得 \frac{(x_1+\lambda x_2)(x_1-\lambda x_2)}{4}+(y_1+\lambda y_2)(y_1-\lambda y_2)=1-\lambda ^2
代入解得 x_1=\frac{5-3\lambda}{2},x_2=\frac{5\lambda -3}{2\lambda},\frac{k_{AC}}{k_{AQ}}=\frac{y_1(x_2+2)}{y_2(x_1-2)}=\frac{-\lambda(x_2+2)}{x_1-2}=\frac{3-9\lambda}{1-3\lambda}=3
练习题:设 F_1,F_2 分别是椭圆 \frac{x^2}{3}+y^2=1 的左右焦点,点 A,B 在椭圆上,\overrightarrow{F_1A}=5\overrightarrow{F_2B} ,则点 A 的坐标是 ?( 答案:(0,\pm 1) )
( 正难则反 )5. 设椭圆 \frac{x^2}{a^2}+y^2=1(a>1) ,若以点 A(0,1) 为圆心的圆与椭圆至多有 3 个公共点,求 e 范围?
从反面考虑,若有 4 个公共点,可知在 y 轴两侧各有 2 个交点,可知椭圆的一侧存在一个等腰 \Delta APQ,AP=AQ 。
设 PQ 中点为 M(x_0,y_0) ,则 k_{OM}k_{PQ}=e^2-1=-\frac{1}{a^2} 。因为 k_{AM}k_{PQ}=\frac{y_0-1}{x_0}k_{PQ}=-1 ,
两式相除得 \frac{y_0-1}{y_0}=a^2>2 ,得出 e\in(0,\frac{\sqrt{2}}{2}] 。
( 齐次化 )6. ( 2022 I 卷,T22 )已知 C:\frac{x^2}{6}+\frac{y^2}{3}=1,A(2,1) ,点 M,N 在 C 上,AM\perp AN,AD\perp MN ,D 为垂足,证明:存在定点 Q ,使得 |DQ| 是定值。
方法一:设 MN:y=kx+m ,暴力联立 + 向量得 (2k+3m+1)(2k+m-1)=0 ,得出 MN 过定点 P(\frac{2}{3},-\frac{1}{3}) 。令 Q(\frac{4}{3},\frac{1}{3}) 为 AP 中点,得出 |DQ|=\frac{1}{2}|AP|=\frac{2\sqrt{2}}{3} 是定值。
方法二:先将 C 平移一下,变为 \frac{(x+2)^2}{6}+\frac{(y+1)^2}{3}=1 ,使得 A 点在新坐标的原点上。设 MN:mx+ny=1 ,联立得 (2+4n)(\frac{y}{x})^2+4(m+n)\frac{y}{x}+4m+1=0 ,显然 \frac{y_1y_2}{x_1x_2}=\frac{4m+1}{2+4n}=-1 ,得到 (-\frac{4}{3})m+(-\frac{4}{3})n=1 ,即定点 (\frac{2}{3},-\frac{1}{3}) 。
( 点差法 + 二次代换消元 )7. ( 华附 2024 5 月测试 )已知 E:\frac{x^2}{4}+y^2=1 ,E 上有 3 点 G,S,T ,直线 ST 过点 C(2,2) ,点 M 为 GS 中点且在直线 y=x 上,证明:直线 GT 与直线 y=x 的交点为定点。
设 S(x_1,y_1),T(x_2,y_2),G(x_3,y_3) ,进行一次点差法:\frac{x_1^2}{4}+y_1^2=1,\frac{x_3^2}{4}+y_3^2=1 ,相减得 \frac{y_1-y_3}{x_1-x_3}=-\frac{y_1+y_3}{4(x_1+x_3)}
因为 GT 中点在 y=x 上所以 y_1+y_3=x_1+x_3 得 y_1-y_3=-\frac{1}{4}(x_1-x_3) 。
两式相加得 2y_1=\frac{3}{4}x_1+\frac{5}{4}x_3\implies x_3=\frac{8y_1-3x_1}{5},y_3=\frac{3y_1+2x_1}{5}
代入 GT:\frac{y-y_3}{x-x_3}=\frac{y-y_2}{x-x_2} 得 (5y_2-3y_1-2x_1)x+(8y_1-3x_1-5x_2)y=-3(x_1y_2+x_2y_1)+8y_1y_2-2x_1x_2
设交点为 (m,m) ,代入得 5m(y_1+y_2)-5m(x_1+x_2)=8y_1y_2-2x_1x_2-3(x_1y_2+x_2y_1)
即证明存在 m 使该式恒成立。
由直线 ST 过点 C(2,2),\frac{y_2-2}{x_2-2}=\frac{y_1-2}{x_1-2}\implies x_1(y_2-2)-x_2(y_1-2)=2(y_2-y_1) ,进行二次代换凑出和积:
x_1(y_2-2)+x_2(y_1-2)=\frac{x_1^2(y_2-2)^2-x_2^2(y_1-2)^2}{x_1(y_2-2)-x_2(y_1-2)}=\frac{(4-4y_1^2)(y_2-2)^2-(4-4y_2^2)(y_1-2)^2}{2(y_2-y_1)}=10(y_1+y_2)-8-8y_1y_2
即 x_1y_2+x_2y_1=2(x_1+x_2)+10(y_1+y_2)-8-8y_1y_2 ①
同理有 (x_1-2)y_2-(x_2-2)y_1=-2(x_2-x_1)
(x_1-2)y_2-(x_2-2)y_1=\frac{(x_1-2)^2y_2^2-(x_2-2)^2y_1^2}{(x_1-2)y_2-(x_2-2)y_1}=\frac{(x_1-2)^2(1-\frac{x_2^2}{4})-(x_2-2)^2(1-\frac{x_1^2}{4})}{-2(x_2-x_1)}
即 x_1y_2+x_2y_1=(x_1+x_2)+2(y_1+y_2)-2-\frac{1}{2}x_1x_2 ②
两式比对系数凑配出 8y_1y_2-2x_1x_2 和目标式比对:
4\times$ ② $-$ ① 得 $2(y_1+y_2)-2(x_1+x_2)=8y_1y_2-2x_1x_2-3(x_1y_2+x_2y_1)
对比 5m(y_1+y_2)-5m(x_1+x_2)=8y_1y_2-2x_1x_2-3(x_1y_2+x_2y_1) 得 m=\frac{2}{5} 时恒成立。
故定点为 (\frac{2}{5},\frac{2}{5}) 。
双曲线
概念:平面内到两个焦点 F_1,F_2 的距离的差等于非零常数( 小于 |F_1F_2| )的点的轨迹叫做双曲线。
双曲线就是下列点的集合 P=\set{M|||MF_1|-|MF_2||=2a} ,|F_1F_2|=2c>2a 。
标准方程
\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)\\ 焦点在 x 轴上\frac{y^2}{a^2}-\frac{x^2}{b^2}=1(a>0,b>0) 焦点在 y 轴上
顶点坐标
(\pm a,0) (0,\pm a)
焦点坐标
(\pm c,0) (0,\pm c)
渐近线方程
y=\pm\frac{b}{a}x y=\pm\frac{a}{b}x
\boxed{c^2=a^2+b^2}$,离心率 $\boxed{e=\frac{c}{a}}\ (e>1)
实轴长 =2a 虚轴长 =2b 。
等轴双曲线:a=b 的双曲线。
一般方程:$Ax^2+By^2=1(AB<0)$。
双曲线与它的渐近线无限接近但永不相交,求渐近线方程时,只要令 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=0$ 即可。
第二定义:平面内动点 $M$ 到定点 $F$ 的距离和它到准线 $l:x=\pm\frac{a^2}{c}$ 的距离之比等于 $e$。
- 与两定点 $A_1(-a,0),A_2(a,0)(a\neq 0)$ 连线的斜率之积为 $\frac{b^2}{a^2}=e^2-1$ 的点的轨迹为双曲线。
#### 双曲线焦点三角形的性质
双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\ (a>0,b>0)$ 上异于顶点的点 $P(x_0,y_0)$ 与两焦点构成的 $\Delta PF_1F_2$ 叫做焦点三角形。
以下记 $\angle F_1PF_2=\theta$。
1. 面积 $\boxed{S=\frac{b^2}{\tan\frac{\theta}{2}}=c|y_0|}$。
2. 设 $\angle PF_1F_2=\alpha,\angle PF_2F_1=\beta,P$ 为双曲线右支上一点,则 $\frac{|PF_1|}{\sin\beta}=\frac{|PF_2|}{\sin\alpha}=\frac{|PF_1|-|PF_2|}{\sin\beta-\sin\alpha}=\frac{2a}{\sin\beta-\sin\alpha}=\frac{|F_1F_2|}{\sin(\alpha+\beta)}=\frac{2c}{\sin\theta}$,所以 $\boxed{e=\frac{\sin(\alpha+\beta)}{\sin\beta-\sin\alpha}}$。
3. 若焦点三角形内切圆的圆心为 $I(x_1,y_1)$,与三边的切点分别为 $M,N,R$,则 $|F_1R|-|F_2R|=|F_1M|-|F_2N|=|PF_1|-|PF_2|=2a$,即 $c+x_1-(c-x_1)=2a$,解得 $x_1=a$。
4. 过双曲线焦点 $(c,0)$ 作渐近线 $y=\frac{b}{a}x$ 的垂线,垂足长度为 $b$,形成的三角形满足 $a^2+b^2=c^2$。
#### 双曲线的其它几何性质
- 通径:过双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\ (a>0,b>0)$ 的焦点作垂直于实轴所在的直线,该直线被双曲线截得的弦叫做通径,长度为 $\frac{2b^2}{a}$。
- 弦长公式:设直线 $y=kx+m$ 与双曲线有两个公共点 $M(x_1,y_1),N(x_2,y_2)$,则 $|MN|=\sqrt{(1+k^2)[(x_1+x_2)^2-4x_1x_2]}=\sqrt{(1+\frac{1}{k^2})[(y_1+y_2)^2-4y_1y_2]}
焦半径:双曲线一点 P(x_0,y_0) 与左( 下 )焦点 F_1 或右( 上 )焦点 F_2 之间的线段叫做双曲线的焦半径,分别记作 r_1=|PF_1|,r_2=|PF_2| 。
设 AB 是 \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0) 的一条弦,AB 中点为 M(x_0,y_0) ,则 k_{AB}=\frac{b^2x_0}{a^2y_0} ,\boxed{k_{AB}k_{OM}=e^2-1} 。
已知双曲线 \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0) ,过双曲线的左焦点 F(-c,0) 的直线交双曲线于 A,B 两点,交 y 轴于点 P ,设 \overrightarrow{PF}=\lambda_1\overrightarrow{FA}=\lambda_2\overrightarrow{FB} ,则 \lambda_1+\lambda_2=\frac{2e^2}{1-e^2}
扩展:若 F 改为 x 轴上一点 M(m,0) ,则 \lambda_1+\lambda_2=\frac{2m^2}{a^2-m^2} 。
对于双曲线上一点 P 做切线交两条渐近线于 A,B ,则 S_{\Delta PAB}=ab
证明:OA:\frac{x}{a^2}-\frac{y}{b^2}=0,OB:\frac{x}{a^2}+\frac{y}{b^2}=0,AB:\frac{x_0x}{a^2}-\frac{y_0y}{b^2}=1
设 A(x_1,y_1),B(x_2,y_2),P(x_0,y_0) ,分别代入得 \frac{x_0x_1}{a^2}-\frac{y_0y_1}{b^2}=1,\frac{x_0x_2}{a^2}-\frac{y_0y_2}{b^2}=1
代入 y_1=\frac{b}{a}x_1,y_2=-\frac{b}{a}x_2 得到 \begin{cases}\frac{x_1}{a}(\frac{x_0}{a}-\frac{y_0}{b})=1 \\ \frac{x_2}{a}(\frac{x_0}{a}+\frac{y_0}{b})\end{cases}
相乘:\frac{x_1^2x_2^2}{a^2}(\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2})=1\implies x_1x_2=a^2,OA\cdot OB=\frac{a^2+b^2}{a^2}x_1x_2=a^2+b^2=c^2
\sin\angle AOB=\sin 2\angle AOx=2\sin\angle AOx\cos\angle AOx=2\frac{ab}{c^2} \\ S=\frac{1}{2}OA\cdot OB\sin\angle AOB=ab
好题
若双曲线的一条渐近线过点 (8,-6) ,则其离心率等于 ?
分 2 种情况讨论,焦点在 x 轴上( \frac{b}{a}=\frac{3}{4}\ \ \ e=\frac{5}{4} ),在 y 轴上( \frac{a}{b}=\frac{3}{4}\ \ \ e=\frac{5}{3} )
动圆 M 与圆 C_1:(x+4)^2+y^2=1 ,圆 C_2:(x-4)^2+y^2=9 都外切,则动圆圆心 M 的轨迹方程为 ?
解:圆 C_1(-4,0),r_1=1,C_2(4,0),r_2=3 ,设 M(x,y) ,半径为 r ,则 \begin{cases}
|MC_1|=r+1 \\
|MC_2|=r+3
\end{cases}
即 |MC_2|-|MC_1|=2<|C_1C_2| ,所以 M 的轨迹为以 C_1,C_2 为焦点,2a=2 的双曲线的左支 ,b=\sqrt{15} 。
所以 M 的轨迹方程为 x^2-\frac{y^2}{15}=1\ (x\leq -1) 。
是否存在过点 P(1,-\frac{1}{2}) 的直线 l 与双曲线 \frac{x^2}{2}-y^2=1 相交于 A,B 两点,且满足 P 是线段 AB 的中点?若存在,求出直线 l 的方程;若不存在,请说明理由。
( 点差法 )解:设 l:y=k(x-1)-\frac{1}{2},A(x_1,y_1),B(x_2,y_2) ,则 \begin{cases}
\frac{x_1^2}{2}-y_1^2=1 \\
\frac{x_2^2}{2}-y_2^2=1
\end{cases} ,
两式相减得 (x_1-x_2)(x_1+x_2)=2(y_1-y_2)(y_1+y_2) ,因为 P(1,-\frac{1}{2}) 为线段 AB 的中点,则
x_1+x_2=2,y_1+y_2=-1,k=\frac{y_1-y_2}{x_1-x_2}=\frac{x_1+x_2}{2(y_1+y_2)}=-1\implies l:y=-x+\frac{1}{2}
联立 \begin{cases}
y=-x+\frac{1}{2} \\
\frac{x^2}{2}-y^2=1
\end{cases} 消去 y 可得 2x^2-4x+5=0,\Delta<0 ,方程无实根,故 l 不存在。
[ 安徽十校联盟 2023 期中 ] 已知双曲线 C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\ (a>0,b>0) 的左、右焦点分别为 F_1,F_2 ,焦距为 4 ,点 M 在圆 E:x^2+y^2+4x-8y+16=0 上,且 C 的一条渐近线上存在点 N ,使得四边形 OMNF_2 为平行四边形,O 为坐标原点,则 C 的离心率的取值范围为( )
\text{A.} [2,+\infty)\ \ \ \ \ \ \text{B.} [\sqrt{3},+\infty)\ \ \ \ \ \ \text{C.} [4,+\infty)\ \ \ \ \ \ \text{D.} (1,\sqrt{3})
答案:\text{A} 。
已知直线 y=ax+1 与双曲线 3x^2-y^2=1 交于 A,B 两点。
$(2)$ 是否存在这样的实数 $a$,使 $A,B$ 两点关于直线 $y=\frac{1}{2}x$ 对称?若存在,请求出 $a$ 的值;若不存在,请说明理由。
解:(1) 联立 \begin{cases}
y=ax+1\\
3x^2-y^2=1
\end{cases} 消去 y 得 (3-a^2)x^2-2ax-2=0 ,依题意 \begin{cases}
3-a^2\neq 0\\
\Delta >0
\end{cases}\\
x_1+x_2=\frac{2a}{3-a^2} \\
x_1x_2=\frac{-2}{3-a^2}
\end{cases}
\ \ \ \ \ \ \ \ \ \ \ \ \ \because$ 以 $AB$ 为直径的圆过坐标原点 $O\ \ \ \therefore OA\perp OB,\ \overrightarrow{OA}\cdot\overrightarrow{OB}=x_1x_2+y_1y_2=0\ \ \ \ \ \ \because y_1y_2=a^2x_1x_2+a(x_1+x_2)+1
\ \ \ \ \ \ \ \ \ \ \ \ \ \therefore x_1x_2+y_1y_2=(a^2+1)x_1x_2+a(x_1+x_2)+1=(a^2+1)\cdot\frac{-2}{3-a^2}+\frac{2a^2}{3-a^2}+1=0\implies a=\pm 1
---
( **齐次化** )6. 已知 $C:x^2+y^2=4$,$A(-2,0),B(2,0)$,$P$ 在 $x=4$ 上,$PA,PB$ 与 $C$ 交于 $M(x_1,y_1),N(x_2,y_2)$,求直线 $MN$ 的定点?
解:设 $P(4,t)\implies 3k_{PA}=k_{PB},MN:my=x+t$,因此 $\frac{y_2}{x_2-2}=\frac{3y_1}{x_1+2}\implies\frac{y_2}{my_2-(t+2)}=\frac{3y_1}{my_1+(2-t)}\implies 2my_1y_2=(3t+6)(y_1+y_2)-(4t+4)y_2\implies \frac{-4m(t+1)(t+2)}{m^2+1}=-4(t+1)y_2
所以 k_{PB}k_{BM}=-3 ,再设 y=kx+3\dots
设 F_1,F_2 为双曲线 C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0) 的左右焦点,A 是右支上一点,\Delta AF_1F_2 内切圆圆心为 M ,半径为 a ,\exist \lambda\in\R,\overrightarrow{AM}+2\overrightarrow{OM}=\lambda\overrightarrow{OF_2} ,则 C 的离心率为 ?
得到 M(a,a)\implies A(3a-\lambda c,3a),AF_2=2c-a=ex_A-a ,因此 x_A=2a,e=2
抛物线
概念:平面内与一个定点 F 和一条定直线 l ( 不经过点 F )的距离相等的点的轨迹叫做抛物线。
标准方程
y^2=2px\ (p>0) y^2=-2px\ (p>0) x^2=2py\ (p>0) x^2=-2py\ (p>0)
开口方向
向右
向左
向上
向下
焦点坐标
(\frac{p}{2},0) (-\frac{p}{2},0) (0,\frac{p}{2}) (0,-\frac{p}{2})
准线
x=-\frac{p}{2} x=\frac{p}{2} y=-\frac{p}{2} y=\frac{p}{2}
抛物线的离心率 e=1 。
通径:过抛物线的焦点作垂直于对称轴的直线,交抛物线于 AB ,线段 AB 就是抛物线的通径,长为 2p ,是所有过焦点的弦中最短的。
抛物线焦点弦的性质
1. $|AF|=|AA_1|=x_1+\frac{p}{2},|BF|=|BB_1|=x_2+\frac{p}{2},|AB|=x_1+x_2+p$。
2. $x_1x_2=\frac{p^2}{4},y_1y_2=-p^2$。
证明:当直线 $AB$ 的斜率存在时,设 $AB:y=k(x-\frac{p}{2}),k\neq 0$,联立抛物线方程和直线方程得 $y^2-\frac{2p}{k}y-p^2=0$。
易知 $\Delta>0$,所以 $y_1y_2=-p^2,x_1x_2=\frac{y_1^2}{2p}\frac{y_2^2}{2p}=\frac{p^2}{4}$,同理可证直线 $AB$ 的斜率不存在时,命题也成立。
3. 以 $|AB|$ 为直径的圆与抛物线的准线相切。
证明:设 $AB$ 中点为 $D$,$D$ 到准线的距离为 $d$,则 $d=\frac{|AA_1|+|BB_1|}{2}=\frac{|AB|}{2}$,原命题得证。
4. 以 $|AF|$ 为直径的圆与 $y$ 轴相切。
5. $\frac{1}{|AF|}+\frac{1}{|BF|}=\frac{2}{p}
证明:当直线 AB 的斜率存在时,\frac{1}{|AF|}+\frac{1}{|BF|}=\frac{1}{|AA_1|}+\frac{1}{|BB_1|}=\frac{1}{x+\frac{p}{2}}+\frac{1}{x_2+\frac{p}{2}}=\frac{x_1+x_2+p}{x_1x_2+\frac{p}{2}(x_1+x_2)+\frac{p^2}{4}}=\frac{x_1+x_2+p}{\frac{p^2}{4}+\frac{p}{2}(x_1+x_2)+\frac{p^2}{4}}=\frac{2}{p}
同理可证直线 AB 的斜率不存在时,命题也成立。
若直线 AB 的倾斜角为 \alpha ,则 |AB|=\frac{2p}{\sin^2\alpha}
证明:当直线 AB 的斜率存在时,设 AB:y=k(x-\frac{p}{2}),k\neq 0 ,由 \begin{cases} y=k(x-\frac{p}{2}) \\ y^2=2px\end{cases} 得 ky^2-2py-kp^2=0 。
易知 \Delta>0,y_1+y_2=\frac{2p}{k},y_1y_2=-p^2,|AB|=\sqrt{(1+\frac{1}{k^2})[(y_1+y_2)^2-4y_1y_2]}=\sqrt{1+\frac{1}{k^2}}\cdot\frac{2p\sqrt{1+k^2}}{|k|}=\frac{2p(1+k^2)}{k^2}=\frac{2p(1+\tan^2\alpha)}{\tan^2\alpha}=\frac{2p}{\sin^2\alpha}
当直线 AB 的斜率不存在时,|AB|=2p=\frac{2p}{\sin^2 90\degree} ,命题也成立。
推广:|AF|=\frac{p}{1-\cos\alpha},|BF|=\frac{p}{1+\cos\alpha} ,O 到 AB 的距离 =\frac{p\sin\alpha}{2},S_{\Delta AOB}=\frac{p^2}{2\sin\theta}
注:若抛物线为 x^2=\pm 2py ,将上述 \cos 换为 \sin ,\sin 换为 \cos 。
设 AB:x=my+\frac{p}{2} 即可通过斜率相等证明。
A_1F\perp B_1F
对于 y^2=2px(p>0) ,当直线过点 (a,0) 与抛物线交于 P,Q ,则 k_{OP}k_{OQ}=-\frac{2p}{a} 。
对于 y^2=2px ,AB 为其一条弦,则 k_{AB}=\frac{2p}{y_1+y_2} ;对于 x^2=2py ,则 k_{AB}=\frac{x_1+x_2}{2p} 。
对于 x^2=2py ,过其上一点 P(x_1,y_1) 做切线 y=kx+(y_1-kx_1) ,联立得 \Delta=pk^2-2x_1k+2y_1=0\implies k=\frac{x_1}{p} ,即切线为 y=\frac{x_1}{p}-\frac{x_1^2}{2p} 。
好题
过点 Q(4,1) 作抛物线 y^2=8x 的弦 AB ,恰被点 Q 平分,则弦 AB 所在直线的方程为 ?
( 点差法 )解:设 A(x_1,y_1),B(x_2,y_2) ,则 \begin{cases} y_1^2=8x_1 (1) \\ y_2^2=8x_2 (2)\end{cases} ,因为 Q(4,1) 是 AB 中点,所以 \begin{cases} x_1+x_2=8 \\ y_1+y_2=2 \end{cases}(3)
---
2. 已知抛物线 $C:y^2=4x$ 的焦点为 $F$,直线 $l$ 过焦点 $F$ 与 $C$ 交于 $A,B$ 两点,以 $AB$ 为直径的圆与 $y$ 轴交于 $D,E$ 两点,且 $|DE|=\frac{4}{5}|AB|$,则直线 $l$ 的方程为_____
解:设 $|AB|=2r(2r\geq 4)$,$AB$ 的中点为 $M$,作 $MN\perp y$ 轴于点 $N$,过 $A,B$ 分别作准线 $l:x=-1$ 的垂线,垂足为 $A_1,B_1
显然 2(|MN|+1)=|AA_1|+|BB_1|=|AF|+|BF|=|AB|=2r ,所以 |MN|=r-1,|DE|=2\sqrt{r^2-(r-1)^2}=\frac{8}{5}r
解得 r=\frac{5}{2}\ \text{or}\ \frac{5}{8} ( 舍 ),所以 M_x=\frac{3}{2}\ \ \ \text{} 设直线 l:y=k(x-1),A(x_1,y_1),B(x_2,y_2) 。
联立 \begin{cases} y=k(x-1) \\ y^2=4x\end{cases} 得 k^2x^2-(2k^2+4)x+k^2=0\implies x_1+x_2=\frac{2k^2+4}{k^2}=3 ,解得 k=\pm 2 。
故直线 l 的方程为 2x\pm y-2=0 。
( 多选 )已知点 F 是抛物线 y^2=2px\ (p>0) 的焦点,AB,CD 是经过点 F 的弦,且 AB\perp CD ,直线 AB 的斜率为 k 且 k>0 ,A,C 两点在 x 轴上方,以下一定成立的有( )
\text{A.}\ \frac{1}{|AB|}+\frac{1}{|CD|}=\frac{1}{2p}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{B.}$ 若 $|AF|\cdot|BF|=\frac{4}{3}p^2$,则 $k=\frac{\sqrt{3}}{3}
\text{C.}\ \overrightarrow{OA}\cdot\overrightarrow{OB}=\overrightarrow{OC}\cdot\overrightarrow{OD}\ \ \ \ \ \ \ \ \text{D.}$ 四边形 $ACBD$ 面积的最小值为 $16p^2
答案:\text{AC}
解析:\text{A.} 由题得 k_{CD}=-\frac{1}{k} ,设 AB:y=k(x-\frac{p}{2}) ,联立 \begin{cases} y=k(x-\frac{p}{2}) \\ y^2=2px\end{cases} 得
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{}$ $k^2x^2-p(k^2+2)x+\frac{1}{4}k^2p^2=0\implies x_1+x_2=\frac{p(k^2+2)}{k^2},x_1x_2=\frac{1}{4}p^2\implies |AB|=x_1+x_2+p=\frac{2p(k^2+1)}{k^2}
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{}$ 同理 $|CD|=2p(1+k^2)$,则有 $\frac{1}{|AB|}+\frac{1}{|CD|}=\frac{1}{2p}
\ \ \ \ \ \ \ \ \ \text{}$ $\text{B.}$ $|AF|\cdot|BF|=(x_1+\frac{p}{2})(x_2+\frac{p}{2})=p^2+\frac{p^2}{k^2}=\frac{4}{3}p^2\implies k=\sqrt{3}
\ \ \ \ \ \ \ \ \ \text{}$ $\text{C.}$ $\overrightarrow{OA}\cdot\overrightarrow{OB}=x_1x_2+y_1y_2=\frac{1}{4}p^2+k^2(x_1-\frac{p}{2})(x_2-\frac{p}{2})=-\frac{3}{4}p^2$,与 $k$ 无关,同理 $\overrightarrow{OC}\cdot\overrightarrow{OD}=-\frac{3}{4}p^2
---
( **同构** )4. ( $2011$ 浙江卷 )已知抛物线 $C_1:x^2=y$,圆 $C_2:x^2+(y-4)^2=1$ 的圆心为点 $M$。已知 $P$ 是抛物线 $C_1$ 上的点( 异于原点 ),过点 $P$ 作圆 $C_2$ 的两条切线,分别交 $C_1$ 于点 $A,B$,若过点 $M,P$ 两点的直线 $l$ 垂直于 $AB$,求直线 $l$ 的方程。
设 $P(x_0,x_0^2),A(x_1,x_1^2),B(x_2,x_2^2)$,则 $k_{AB}=x_1+x_2$,$PA:y-x_0^2=(x_1+x_0)(x-x_0)$,即 $(x_1+x_0)x-y-x_1x_0=0$。
从而 $1=\frac{|4+x_1x_0|}{\sqrt{(x_1+x_0)^2+1}}$,整理得 $(1-x_0^2)x_1^2-6x_1x_0+x_0^2-15=0$,同理 $(1-x_0^2)x_2^2-6x_2x_0+x_0^2-15=0$。
显然 $x_1,x_2$ 是方程 $(1-x_0^2)x^2-6xx_0+x_0^2-15=0$ 的两根,$x_1+x_2=\frac{6x_0}{1-x_0^2}=k_{AB}$,因为 $k_l=\frac{x_0^2-4}{x_0}$。
所以可以解得 $x_0^2=\frac{23}{5},l:y=\pm\frac{3\sqrt{115}}{115}x+4$。
---
( **向量** )5. 已知抛物线 $y=x^2,A(-\frac{1}{2},\frac{1}{4}),B(\frac{3}{2},\frac{9}{4})$,抛物线上的 $P(x,y)(-\frac{1}{2}<x<\frac{3}{2})$,过点 $B$ 作直线 $AP$ 的垂线,垂足为 $Q$,求 $|PA|\cdot|PQ|$ 的最大值。
设 $AB$ 中点为 $M(\frac{1}{2},\frac{5}{4})$,从而 $|PA|\cdot|PQ|=-\overrightarrow{PA}\cdot\overrightarrow{PQ}=-\overrightarrow{PA}\cdot(\overrightarrow{PB}+\overrightarrow{BQ})=-\overrightarrow{PA}\cdot\overrightarrow{PB}=(\frac{\overrightarrow{PA}-\overrightarrow{PB}}{2})^2-(\frac{\overrightarrow{PA}+\overrightarrow{PB}}{2})^2=2-|PM|^2=(x+\frac{1}{2})^3(\frac{3}{2}-x)=\frac{1}{3}(x+\frac{1}{2})(x+\frac{1}{2})(x+\frac{1}{2})(\frac{9}{2}-3x)\leq \frac{1}{3}[\frac{(x+\frac{1}{2})+(x+\frac{1}{2})+(x+\frac{1}{2})+(\frac{9}{2}-3x))}{4}]^4\leq\frac{27}{16}$。
当且仅当 $x=1$ 时取等号。
---
( **齐次化** )6. 抛物线 $C:y^2=2px$,设 $A,B$ 为抛物线上的点,$OA\perp OB$,证明 $AB$ 过定点。
设 $AB:mx+ny=1$,联立 $y^2=2px(mx+ny)\implies y^2-2pnxy-2pmx^2=0$,同时除以 $x^2$ 得:
$(\frac{y}{x})^2-2pn\frac{y}{x}-2pm=0\implies\frac{y_1}{x_1}\frac{y_2}{x_2}=-2pm=-1$,得 $2pm=1$,因此定点为 $(2p,0)$。
## 其他问题
#### 共焦点问题
已知 $F_1,F_2$ 为椭圆( 离心率 $e_1$ )和双曲线( 离心率 $e_2$ )的公共焦点,$P$ 是一个公共点,$\angle F_1PF_2=\theta$,则 $\boxed{\frac{\sin^2\frac{\theta}{2}}{e_1^2}+\frac{\cos^2\frac{\theta}{2}}{e_2^2}=1}$,因此可以推出 $e_1e_2\geq 2\sin\frac{\theta}{2}\cos\frac{\theta}{2}=\sin\theta$。
#### 极点极线问题
设圆锥曲线 $C:Ax^2+By^2+Cxy+Dx+Ey+F=0$,平面上任意一点 $P(x_0,y_0)$,则极点 $P$ 关于 $C$ 的极线方程是 $Ax_0x+By_0y+C\frac{x_0y+y_0x}{2}+D\frac{x_0+x}{2}+E\frac{y_0+y}{2}+F=0$。也就是说:
1. $x^2,y^2$ 换成 $x_0x,y_0y$。
2. $xy$ 换成 $\frac{x_0y+y_0x}{2}$。
3. $x,y$ 换成 $\frac{x_0+x}{2},\frac{y_0+y}{2}$。
4. 常数项不变。
对于椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,$P$ 的极线方程为 $\boxed{\frac{x_0x}{a^2}+\frac{y_0y}{b^2}=1}$;当 $P$ 是焦点时,极线 $=$ 准线,即 $x=\frac{a^2}{c}
极点 P 和极线 l 的【位置关系】满足:
【部分证明】
设 $CD:x=ty+m,C(x_1,y_1),D(x_2,y_2),N(m,0)$,则 $y_1+y_2=\frac{-2b^2mt}{a^2+b^2t^2},y_1y_2=\frac{b^2m^2-a^2b^2}{a^2+b^2t^2}
注意到 \displaystyle m(y_1+y_2)+2ty_1y_2=\frac{-2a^2b^2t}{a^2+b^2t^2}=\frac{a^2}{m}(y_1+y_2)
有 AC:x=\frac{x_1+a}{y_1}y-a,BD:x=\frac{x_2-a}{y_2}y+a ,联立得
\frac{ty_1+m+a}{y_1}y-a=\frac{ty_2+m-a}{y_2}y+a\implies\frac{m+a}{y_1}y-\frac{m-a}{y_2}y=2a
\begin{aligned}y_M&=\frac{2ay_1y_2}{m(y_2-y_1)+a(y_1+y_2)}\\x_M&=\frac{a^2(y_2-y_1)+2aty_1y_2+am(y_1+y_2)}{m(y_2-y_1)+a(y_1+y_2)}\\&=\frac{a^2(y_2-y_1)+a\cdot\frac{a^2}{m}(y_1+y_2)}{m(y_2-y_1)+a(y_1+y_2)}=\frac{a^2}{m}\end{aligned}
【性质】
过 P 作直线 PQ ,交极线 MN 于 Q ,交椭圆于 A,B 两点 \iff\frac{|PA|}{|PB|}=\frac{|QA|}{|QB|} ( 调和点列 )。
【例题】
设 C:\frac{x^2}{4}+\frac{y^2}{3}=1 ,过 C 的右焦点,且斜率不为 0 的直线交 C 于 M,N 两点,直线 AM,BN 交于点 Q ,证明:点 Q 在直线 x=4 上。
解:显然右焦点 (1,0) 是极点,那么极线就是 \frac{x}{4}=1 ,即 x=4 。
与定值 \frac{2}{e} 有关的问题:
若 AB 是过椭圆 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 的焦点 F 的焦点弦,AB 的垂直平分线交 x 轴于点 M ,则 \frac{|AB|}{|FM|} 为定值 \frac{2}{e} 。
证明:设 F 为左焦点,以 F 为极点,x 轴为极轴建立极坐标系,得极坐标方程 \rho = \frac{ep}{1-e\cos\theta} ,
所以 |AB|=\rho_1+\rho_2=\frac{2ep}{1-e^2\cos^2\theta} ,|FM|=\frac{1}{|\cos\theta|}|\frac{\rho_1-\rho_2}{2}|=\frac{e^2p}{1-e^2\cos^2\theta}\implies\frac{|AB|}{|FM|}=\frac{2}{e}
椭圆 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 的左焦点为 F ,在 x 轴上点 F 右侧有一点 A ,以 FA 为直径作半径为 R 的圆,在 x 轴上方部分交于 N,M 两点,则 \frac{|FM|+|FN|}{R}=\frac{2}{e}
证明:设圆为 [x-(R-c)]^2+y^2=R^2 ,联立得 x_1+x_2=\frac{2a^2(R-c)}{c^2},|FM|+|FN|=a+ex_1+a+ex_2=\frac{2R}{e}
若 AB 为椭圆 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 焦点 F 的弦,FM 为与焦点 F 对应的焦准距,则 \frac{|AB||FM|}{|FA||FB|}=\frac{2}{e}
证明:同 1 建极坐标系,|FM|=p,|FA|=\frac{ep}{1-e\cos\theta},|FB|=\frac{ep}{1+e\cos\theta},|AB|=|FA|+|FB|=\frac{2ep}{1-e^2\cos^2\theta},|FA||FB|=\frac{e^2p^2}{1-e^2\cos^2\theta} 。
已知椭圆 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 的左右焦点分别为 F_1,F_2,A(-a,0),B(a,0) ,点 P 是椭圆上的点( 不与 A,B 重合 ),\angle APB=2\alpha,\angle F_1PF_2=2\beta,|\tan\beta\tan 2\alpha| 为定值 \frac{2}{e}
光学性质
【椭圆】:设 F_1,F_2 是椭圆的两个焦点,从 F_1 出发的光线经过反射必经过 F_2 。
【双曲线】:设 F_1,F_2 是双曲线的两个焦点,从 F_1 出发的光线经过反射后的反向延长线必经过 F_2 。
【抛物线】:设 F 为焦点,从 F 出发的光线经过反射后,平行于对称轴。
【椭圆+抛物线】设 P 为反射点,AB 为 P 处的切线,PT 平分 \angle F_1PF_2 ,则 PT\perp AB
仿射变换
设 a>0,b>0 ,将原来曲线上的每个点的横坐标乘以 a ,纵坐标乘以 b ,形成了新的曲线。
【性质】:
对原来的两条曲线作仿射变换,交点数不变。
对曲线 f(x,y)=0 作仿射变换,曲线变为 f(\frac{x}{a},\frac{y}{b})=0 。
对面积为 S 的曲线作仿射变换,面积变为 abS 。
对直线 Ax+By+C=0 作仿射变换,变为 \frac{A}{a}x+\frac{B}{b}y+C=0
【推论】
椭圆 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 与直线 Ax+By+C=0 相切的充要条件是 A^2a^2+B^2b^2=C^2 。
椭圆面积为 \pi ab
阿基米德三角形
圆锥曲线的弦和过弦端点的两条切线所围成的三角形称为阿基米德三角形,该弦称为底边。
【2006高考卷】已知抛物线 x^2=4y 的焦点为 F ,点 A,B 是抛物线上两个动点,且 \overrightarrow{AF}=\lambda\overrightarrow{FB}(\lambda>0) ,过 A,B 两点分别作抛物线的切线,设其交点为 M ,证明:\overrightarrow{FM}\cdot\overrightarrow{AB} 是定值。
解:设 A(x_1,\frac{x_1^2}{4}),B(x_2,\frac{x_2^2}{4}) ,由 \overrightarrow{AF}=\lambda\overrightarrow{FB} 得 x_1x_2=-4 。
已知抛物线方程为 y=\frac{1}{4}x^2 ,求导得 y`=\frac{1}{2}x ,所以过 A,B 两点的切线方程是 y=\frac{1}{2}x_1x-\frac{1}{4}x_1^2,y=\frac{1}{2}x_2x-\frac{1}{4}x_2^2
交点 M(\frac{x_1+x_2}{2},-1) ,所以 \overrightarrow{FM}=(\frac{x_1+x_2}{2},-2),\overrightarrow{AB}=(x_2-x_1,\frac{x_2^2-x_1^2}{4}) ,从而 \overrightarrow{FM}\cdot\overrightarrow{AB}=0
扩展开来,对于抛物线 y^2=2px(p>0) 的焦点 F 的直线交抛物线于 A,B 两点,过 A,B 两点的切线交于 M ,则 \boxed{\overrightarrow{FM}\cdot\overrightarrow{AB}=0} ,并且 M 在准线上\boxed{|MF|^2=|FA|\cdot|FB|} 。( 证明 MA\perp MB 即可,射影定理 )
对于椭圆 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 的左焦点 F 任意做一条直线 AB ,交椭圆于 A,B 两点,分别过 A,B 作椭圆的切线交于点 M ,则 M 在左准线上\boxed{\overrightarrow{FM}\cdot\overrightarrow{AB}=0} 。( 通过设 A(a\cos\theta_1,b\sin\theta_1) 等证明 )
柯西不等式
引理
设 \overrightarrow{a}=(x_1,y_1),\overrightarrow{b}=(x_2,y_2) ,由 |\overrightarrow{a}|\cdot|\overrightarrow{b}|\geq\overrightarrow{a}\cdot\overrightarrow{b}
得 (x_1^2+y_1^2)\cdot(x_2^2+y_2^2)\geq(x_1x_2+y_1y_2)^2 ,当且仅当 \frac{x_1}{x_2}=\frac{y_1}{y_2} 时等号成立。
例题
设椭圆 C:\frac{x^2}{16}+\frac{y^2}{12}=1,M(2,\sqrt{2}) ,过点 P(-8,0) 的直线与 C 交于 A,B 两点,求 \Delta ABF 面积的最大值。
设 A(x_1,y_1),B(x_2,y_2) ,由 P,A,B 三点共线得 k_{PA}=k_{PB}\implies\frac{y_1}{x_1+8}=\frac{y_2}{x_2+8}\implies x_2y_1-x_1y_2=8(y_2-y_1)
S_{\Delta ABF}&=S_{\Delta PBF}-S_{\Delta PAF}=\frac{1}{2}|PF||y_1-y_2| \\
&=\frac{1}{2}\times 6\times |y_1-y_2|=\frac{3}{8}|x_1y_2-x_2y_1| \\
&\leq\frac{3}{8}\sqrt{12\times 16\times (\frac{x_1^2}{16}+\frac{y_1^2}{12})[\frac{y_2^2}{12}+\frac{(-x_2)^2}{16}]} \\
&=3\sqrt{3}
\end{aligned}
当且仅当 \frac{x_1x_2}{4}=-\frac{y_1y_2}{3} 时成立。
【天津静海四校 2021 阶段性检测】已知 E:\frac{x^2}{4}+y^2=1,A(-2,0),B(0,1),F_1(-\sqrt{3},0),F_2(\sqrt{3},0),P 为椭圆上一动点。C,D 是 E 上两个不同的点,CD//AB ,直线 CD 与 x,y 轴分别交于 M,N 两点,且 \overrightarrow{MC}=\lambda\overrightarrow{CN},\overrightarrow{MD}=\mu\overrightarrow{DN} ,求 \lambda+\mu 的取值范围。
显然 k_{AB}=\frac{1}{2} ,可设 CD 的方程为 y=\frac{1}{2}x+m(m\neq\pm 1) ,得 M(-2m,0),N(0,m) ,设 C(x_1,y_1),D(x_2,y_2)
由 \overrightarrow{MC}=\lambda\overrightarrow{CN} ,得 (x_1+2m,y_1)=\lambda(-x_1,m-y_1)\implies\begin{cases}x_1=\frac{-2m}{1+\lambda} \\ y_1=\frac{\lambda m}{1+\lambda}\end{cases}
代入椭圆方程并化简得 (m^2-1)\lambda^2-2\lambda+m^2-1=0 ,把 \lambda 换成 \mu 得到同构方程,因此 \lambda,\mu 可看成 (m^2-1)x^2-2x+m^2-1=0 的两根。
得到 \lambda+\mu=\frac{2}{m^2-1} ,因为 C,D 都在 E 上,由柯西不等式
2=(\frac{x^2}{4}+y^2)[(-1)^2+1]\geq(-\frac{1}{2}x+y)^2=m^2
当且仅当 C,D 重合时等号成立,与题意不符,故 0\leq m^2<2 且 m^2\neq 1 ,所以 \lambda+\mu=\frac{2}{m^2-1}\in(-\infty,-2]\cup(2,\infty)
拉格朗日恒等式
椭圆形式的拉格朗日恒等式
设 A(x_1,y_1),B(x_2,y_2) 是椭圆 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 上非顶点的两点,则:
1=(\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2})(\frac{x_2^2}{a^2}+\frac{y_2^2}{b^2})=(\frac{x_1x_2}{a^2}+\frac{y_1y_2}{b^2})^2+\frac{(x_1y_2-x_2y_1)^2}{a^2b^2}
引理 - 三角形面积公式
\overrightarrow{OA}=(x_1,y_1),\overrightarrow{OB}=(x_2,y_2)$,则 $S_{\Delta OAB}=\frac{1}{2}|x_1y_2-x_2y_1|
因此,拉格朗日恒等式可用于处理三角形面积定值问题。当 (\frac{x_1x_2}{a^2}+\frac{y_1y_2}{b^2})^2=0 时,S_{\max}=\frac{ab}{2}
引理 - 和积关系 & 合比关系
已知 A(x_1,y_1),B(x_2,y_2) 在椭圆 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 上,直线 AB 经过 M(m,0) 满足:
2x_1x_2=(\frac{a^2}{m}+m)(x_1+x_2)-2a^2
直线 AB 经过 N(0,n) 满足:
2y_1y_2=(\frac{b^2}{n}+n)(y_1+y_2)-2b^2
可用点差法证明。
例题
椭圆 E:\frac{x^2}{16}+\frac{y^2}{4}=1,P(0,1),Q(0,2) ,过点 P 的直线 l:y=kx+1 交椭圆 E 于 A,B 两点,求 S_{\Delta ABQ} 最大值。
由 A,B,P 三点共线得 \frac{y_1-1}{x_1}=\frac{y_2-1}{x_2} ,得
(1)\ \ \ \ \ x_1y_2-x_2y_1=x_1-x_2
(2)\ \ \ \ \ 2y_1y_2=5(y_1+y_2)-8
(3)\ \ \ \ \ x_1x_2=-6(y_1+y_2)
由 (y_1+y_2)^2-(y_1-y_2)^2=4y_1y_2 和 (2) 得 (y_1+y_2)^2-(y_1-y_2)^2=10(y_1+y_2)-16
配方得 (y_1+y_2-5)^2=9+(y_1-y_2)^2\geq 9
所以 y_1+y_2\leq 2 当且仅当 y_1=y_2=1 时成立( y_1+y_2\geq 8 舍去 )
由拉格朗日恒等式得
1&=(\frac{x_1x_2}{16}+\frac{y_1y_2}{4})^2+\frac{(x_1y_2-x_2y_1)^2}{64} \\
&=(\frac{y_1+y_2}{4}-1)^2+\frac{(x_1y_2-x_2y_1)^2}{64} \\
&\geq \frac{1}{4}+\frac{(x_1y_2-x_2y_1)^2}{64}
\end{aligned}
得 |x_1y_2-x_2y_1|\leq 4\sqrt{3} ,所以 S=\frac{1}{2}|PQ||x_1-x_2|=\frac{1}{2}|x_1y_2-x_2y_1|\leq 2\sqrt{3}
已知椭圆 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) ,A,B 是其上两动点,k_{OA}\cdot k_{OB}=-\frac{b^2}{a^2} ,点 M 满足 \overrightarrow{OM}=\lambda\overrightarrow{OA}+\mu\overrightarrow{OB} 且 \lambda^2+\mu^2=1 ,证明 M 在椭圆上。
设 A(x_1,y_1),B(x_2,y_2) ,易得 \frac{x_1x_2}{a^2}+\frac{y_1y_2}{b^2}=0 ,点 \frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}=1,\frac{x_2^2}{a^2}+\frac{y_2^2}{b^2}=1
因此 M(\lambda x_1+\mu x_2,\lambda y_1+\mu y_2) ,代入椭圆方程联立得
\lambda^2(\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2})+\mu^2(\frac{x_2^2}{a^2}+\frac{y_2^2}{b^2})+2\lambda\mu(\frac{x_1x_2}{a^2}+\frac{y_1y_2}{b^2})=1
得到 \lambda^2+\mu^2=1 ,结论成立。( 每一步都是等价关系 )
参数方程
曲线方程
参数方程
三角消元
直线 y-y_0=\tan\alpha(x-x_0)(\alpha 为倾斜角 )
\begin{cases}x=x_0+t\cos\alpha \\ y=y_0+t\sin\alpha\end{cases}(t 为参数 ) P(x_0+t\cos\alpha,y_0+t\sin\alpha)
圆 (x-a)^2+(y-b)^2=r^2(r>0)
\begin{cases}x=r\cos\alpha+a \\ y=r\sin\alpha+b\end{cases}(\alpha 为参数 ) P(r\cos\alpha+a,r\sin\alpha+b)
椭圆 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)
\begin{cases}x=a\cos\alpha \\ y=b\sin\alpha\end{cases}(\alpha 为参数 ) P(a\cos\alpha,b\sin\alpha)
双曲线 \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)
\begin{cases}x=\frac{a}{\cos\alpha} \\ y=b\tan\alpha\end{cases}(\alpha 为参数 ) P(\frac{a}{\cos\alpha},b\tan\alpha)
本质就是利用 \sin^2\alpha+\cos^2\alpha=1 。
例题
过椭圆 C:\frac{x^2}{4}+\frac{y^2}{9}=1 上一点 P 作与直线 l:2x+y-6=0 夹角为 30\degree 的直线,交于 A ,求 |PA| 的最值。
设 P(2\cos\theta,3\sin\theta) ,距离 d(P,l)=\frac{\sqrt{5}}{5}|4\cos\theta+3\sin\theta-6| ,
则 |PA|=\frac{d}{\sin 30\degree}=\frac{2\sqrt{5}}{5}|5\sin(\theta+\alpha)-6| ,其中 \alpha 为锐角。所以最值为 \frac{2\sqrt{5}}{5} 和 \frac{22\sqrt{5}}{5} 。
椭圆 C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) ,A,B,C 为其上三点,满足 \Delta ABC 的重心坐标为 O ,求 S_{\Delta ABC} 。
设 A(a\cos\alpha,b\sin\alpha),B(a\cos\beta,b\sin\beta)\implies C(-a(\cos\alpha+\cos\beta),-b(\sin\alpha+\sin\beta)) ,代入得
(\cos\alpha+\cos\beta)^2+(\sin\alpha+\sin\beta)^2=2+2\cos\alpha\cos\beta+2\sin\alpha\sin\beta=2+2\cos(\alpha-\beta)=1\implies\cos(\alpha-\beta)=-\frac{1}{2}\implies\alpha-\beta=120\degree
|AB|=\sqrt{a^2(\cos\alpha-\cos\beta)^2+b^2(\sin\alpha-\sin\beta)^2}
AB:y=\frac{b(\sin\alpha-\sin\beta)}{a(\cos\alpha-\cos\beta)}(x-a\cos\alpha)+b\sin\alpha\implies b(\sin\beta-\sin\alpha)x+a(\cos\alpha-\cos\beta)y+ab\sin(\alpha-\beta)=0
d(O,AB)=\frac{\frac{\sqrt{3}}{2}ab}{\sqrt{a^2(\cos\alpha-\cos\beta)^2+b^2(\sin\alpha-\sin\beta)^2}}
由重心性质,S_{\Delta ABC}=3S_{\Delta AOB}=\frac{3}{2}|AB|d=\frac{3\sqrt{3}}{4}ab 。
扩展开来,对于平行四边形 OABC ,其中 A,B,C 三点都在椭圆上,则 S=2S_{\Delta AOB}=\frac{\sqrt{3}}{2}ab 。