Treap&替罪羊树 学习笔记

为什么选这两种平衡树： - 这两种平衡树都属于普通平衡树，**不支持序列翻转等操作**。 - 其中，*Treap* 是带旋转普通平衡树中比较好写的一种（相较于 *AVL* 等），**替罪羊树**是无旋普通平衡树中比较好写的一种。 - 二者常数较小。（不过都不可持久化） # Treap Tips：本文中的 *Treap* 都指**带旋转**的平衡树，即将 *fhq-Treap* 排除在外。 ### 1. Treap 的用途 作为一种平衡树，它可以在单次 $\Theta(\log n)$ 内支持[普通平衡树](https://www.luogu.com.cn/problem/P3369)中的所有操作：（与 *BST* 相同） - 单点插入和删除； - 求数的前驱与后继； - 求数的排名或根据排名查数； 其中，鉴于 C++ STL 中有 *set* 的存在，以及平衡树**易写难调的特点**，应尽量采用 *set* 来代替普通平衡树。 但是，*set* 只支持前两种操作，求排名和根据排名查数必须通过手写平衡树实现。 （C++ pb_ds 里好像有个 *rope*，然而我不会用) 其中，*Treap* 常数较小，且依赖随机化，很难被卡。 ### 2. Treap 的核心思想及原理 *Treap* 的出现主要是为了解决 *BST* 被卡的问题。（废话） 与不少平衡树一样，*Treap* 通过旋转的方式解决平衡树退化的问题。 不过，什么时候要旋转呢？与 *AVL* 通过高度决定，*SBT* 通过字数大小决定不同，*Treap* 采用一种简单粗暴的方式决定何时要旋转： **随机化！！！** 我们对每个结点新增一个权值 $dat$，然后采用**二叉堆**的思想进行维护。 （所谓 *Treap*，便是 *Tree* + *Heap* = *Treap*） 具体地说： - 若当前结点的左儿子的 $dat$ 比自身大，则对当前结点右旋； - 反之，若当前结点的右儿子的 $dat$ 比自身大，则对当前结点左旋； 其中，左旋（*zig*）和右旋（*zag*）图示如下：（自制）  由于 $dat$ 是随机的，因此树高的期望为 $\log n$，总复杂度为 $\Theta(n\log n)$。 （然而我并不会证复杂度，而且网上还搜不到） ### 3. Treap 的基本操作 这里以 [P3369 【模板】普通平衡树](https://www.luogu.com.cn/problem/P3369) 为例进行说明。 这里我们采用大根堆维护随机权重。 - 单个结点 ```c++ struct node { int l,r; int val,dat; int siz,cnt; }a[N]; ``` 包括 $l$（左儿子），$r$ （右儿子），$val$（本身权值），$dat$（随机权重），$siz$（子树大小）和 $cnt$（重复个数）。 以下用 $tot$ 表示总结点数。 - 新增结点、建树 ```c++ int Treap::New(int w) { a[++tot].val=w; a[tot].siz=a[tot].cnt=1; a[tot].dat=rand(); return tot; } ``` 建树时，可以先在里面插入 $-\infty$ 和 $+\infty$ 两个结点减少边界判断。 ```c++ void Treap::Build() { New(-inf), New(inf); a[1].r=2, a[1].siz=2; rt=1; } ``` 显然，排好序的数列是可以 $\Theta(n)$ 时间建树的，不过这没什么用。 - 更新与旋转 ```c++ void Treap::update(int x) { a[x].siz=a[a[x].l].siz+a[a[x].r].siz+a[x].cnt; } ``` 旋转时可以传引用，这样更方便。 ```c++ void Treap::zig(int &p) { int q=a[p].l; a[p].l=a[q].r, a[q].r=p, p=q; update(a[p].r), update(p); } ``` ```c++ void Treap::zag(int &p) { int q=a[p].r; a[p].r=a[q].l, a[q].l=p, p=q; update(a[p].l), update(p); } ``` - 插入 根据维护的 $siz$ 信息递归处理，记得随时更新、旋转。 ```c++ void Treap::insert(int &x,int w) { if(x==0) { x=New(w); return ; } if(w<a[x].val) { insert(a[x].l,w); if(a[x].dat<a[a[x].l].dat) zig(x); } else if(w==a[x].val) a[x].cnt++; else { insert(a[x].r,w); if(a[x].dat<a[a[x].r].dat) zag(x); } update(x); } ``` - 删除**（难点）** 若当前结点的 $cnt$ 值大于 $1$，直接将 $cnt$ 减 $1$，再维护信息即可。 若当前结点的 $cnt$ 值为 $1$，情况就难以处理。 不过由于有旋转操作的存在，我们可以**将要删除的结点转到底再删除**。 ```c++ void Treap::erase(int &x,int w) { if(w==a[x].val) { if(a[x].cnt>1) { a[x].cnt--, update(x); return; } if(a[x].l||a[x].r) { //继续向下转 if(a[x].r==0||a[a[x].l].dat>a[a[x].r].dat) { //取左右儿子中较大的 zig(x); erase(a[x].r,w); } else { zag(x); erase(a[x].l,w); } update(x); return; } a[x].cnt=a[x].siz=0, x=0; //善始善终（不必要） return; } else { if(w<a[x].val) erase(a[x].l,w); else erase(a[x].r,w); update(x); } } ``` - 查排名、查值 照 $insert$ 操作一样暴力递归即可。 ```c++ int Treap::getrank(int x,int w) { if(x==0) return 0; if(w<a[x].val) return getrank(a[x].l,w); if(w==a[x].val) return a[a[x].l].siz+1; return a[a[x].l].siz+a[x].cnt+getrank(a[x].r,w); } ``` ```c++ int Treap::getval(int x,int w) { if(x==0) return 0; if(w<=a[a[x].l].siz) return getval(a[x].l,w); if(w<=a[a[x].l].siz+a[x].cnt) return a[x].val; return getval(a[x].r,w-a[a[x].l].siz-a[x].cnt); } ``` - 求前驱、后继**（难点）** 这里我们不采用递归的写法，而是直接展开成循环。（我也不知道为什么要这么做，因为蓝书上是这么搞的） 过程中记录可能成为答案的值即可。 小优化：容易证明后出现的答案一定比先出现的优，因此我们无需取 $\max$ 或 $\min$。 ```c++ int Treap::getprev(int w) { int x=T.rt,ans=0; while(x) { if(a[x].val==w) { if(a[x].l) { x=a[x].l; while(a[x].r) x=a[x].r; return a[x].val; } return ans; } if(w<a[x].val) x=a[x].l; else ans=a[x].val, x=a[x].r; } return ans; } int Treap::getnext(int w) { int x=T.rt,ans=0; while(x) { if(a[x].val==w) { if(a[x].r) { x=a[x].r; while(a[x].l) x=a[x].l; return a[x].val; } return ans; } if(w<a[x].val) ans=a[x].val, x=a[x].l; else x=a[x].r; } return ans; } ``` - 输出平衡树的所有信息 为了调平衡树专门写的，大概没啥意义（ ```c++ void Treap::print() { printf("tot=%d\n",tot); fo(i,1,tot) { printf("i=%d val=%d cnt=%d\n",i,a[i].val,a[i].cnt); printf("l=%d r=%d dat=%d\n",a[i].l,a[i].r,a[i].dat); puts("--------------"); } } ``` ### 4. 例题 - [P3369 【模板】普通平衡树](https://www.luogu.com.cn/problem/P3369) 把上面的东西拼起来即为答案。 [Code](https://www.luogu.com.cn/record/53684222) - [P1486 [NOI2004] 郁闷的出纳员](https://www.luogu.com.cn/problem/P1486) 可以发现，我们难以处理数据结构中全局加，全局减，那么，不如就新建一个参照物 $cur$，让它改变。 简单地说，数据结构中的数 $x$ 的真实值应该是 $x+cur$。 1. `I` 指令时，一个员工 $x$ 进入时我们尝试将 $x+cur$ 插入数据结构。 2. `A` 指令时，我们将 $cur$ 减 $x$； 3. `S` 指令时，我们将 $cur$ 加 $x$，并尝试弹出所有不合法的值； 4. `F` 指令时，我们输出数据结构中第 $x$ 大的数减去 $cur$。 由于涉及到由排名查值，*set* 无法胜任，只能维护一棵普通平衡树。 [Code](https://www.luogu.com.cn/record/53723100) --- # 替罪羊树 ### 1. 替罪羊树的用途 **替罪羊树**（*Scapegoat Tree*）的主要用途实际上和 *Treap* 也差不多，不过有一些别的用途。 - 大致上和别的普通平衡树相同，且常数较小。 - 由于没有旋转，替罪羊树**可以以（均摊）低于线性的复杂度维护单点增量**，比如带插入删除的区间第 $k$ 大。 - 此外，替罪羊树的拍平重构思想指导了 *KD-Tree* 的引出。 ### 2. 替罪羊树的原理 与 *Treap* 不同，替罪羊树不使用旋转来调整树的结构。与之相对，替罪羊树采用对不平衡的子树**直接拍平重构**来保证树的结构。 那么，怎么样的子树需要被重构呢？这里便需要引出一个概念：**平衡因子 $\alpha$**。 **定义**：我们在维护替罪羊树时进行拍平重构的判断时用到的常数为**平衡因子**，记为 $\alpha$。 具体地，如果一个不是叶子的结点 $x$ 满足： $$ \alpha\cdot \operatorname{siz}(x)\leq \max\{\operatorname{siz}(lson_x),\operatorname{siz}(rson_x)\} $$ 则我们将其重构。 由定义可知，一般情况下 $\alpha$ 是一个常数，且满足 $0.5<\alpha<1$。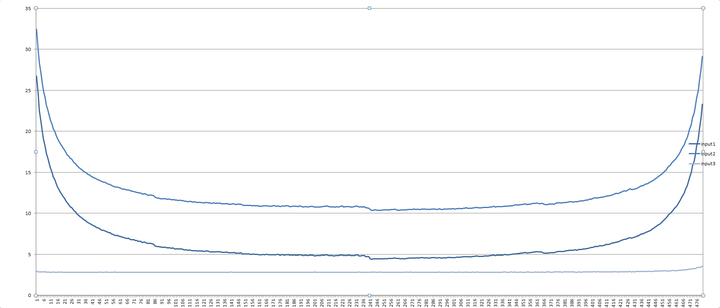 下面是一张从知乎偷来的图：  可以发现，程序运行时间随 $\alpha$ 的增加先下降后上升。原因在于当 $\alpha$ 过小时，我们的重构次数过多；而 $\alpha$ 过大时平衡树易退化，查询复杂度上升。 实践中，一般取 $\alpha=0.75$ 或 $\alpha=0.8$。个人一般取 $\alpha=0.75$。 时间复杂度期望 $\Theta(n\log n)$。关于证明，由于重构之后我们一段时间内树结构都是较为平衡的，不需要经常重构，因此自然地想到使用**势能分析法**。 具体可以参考知乎上的[这个回答](https://www.zhihu.com/question/51891585/answer/234930161)。结论简单来说，就是： **重构的均摊复杂度是 $\Theta(1)$ 的，而且插入的复杂度是 $O(\log n)$ 的**。 ### 3. 替罪羊树的基本操作 这里还是以[P3369 【模板】普通平衡树](https://www.luogu.com.cn/problem/P3369)为例进行说明。 - 单个结点 ```c++ struct node { int l,r; int cnt,siz; int val; }a[N]; ``` 与 *Treap* 类似，少了 $dat$。 - 新增节点、建树 ```c++ int Tree::New(int w) { tot++, a[tot].val=w; a[tot].siz=a[tot].cnt=1; return tot; } void Tree::Build() { New(-inf), New(inf); a[1].r=2, a[1].siz=1; rt=1; } ``` - 更新信息、判断平衡 ```c++ void Tree::update(int x) { a[x].siz=a[a[x].l].siz+a[a[x].r].siz+a[x].cnt; } bool Tree::check(int x) { return a[x].siz*alpha>max(a[a[x].l].siz,a[a[x].r].siz); } ``` - 重构**（难点）** 分两步： 1. 中序遍历子树内的所有结点。 2. 清空结点左右儿子信息并中序建树。 这里是非指针版的，尽量避免出错。 ```c++ void Tree::mark(int x) { if(a[x].l) mark(a[x].l); if(a[x].cnt) id[++cur]=x; if(a[x].r) mark(a[x].r);}void Tree::work(int &x,int l,int r) { if(l>r) { x=0; return; } if(l==r) { x=id[l], a[x].siz=a[x].cnt; return; } int mid=(l+r+1)>>1; x=id[mid]; work(a[x].l,l,mid-1); work(a[x].r,mid+1,r); update(x);}void Tree::rebuild(int &x) { cur=0; mark(x); fo(i,1,cur) a[id[i]].l=a[id[i]].r=a[id[i]].siz=0; work(x,1,cur);} ``` - 插入、删除 插入与 *Treap* 几乎一致。 ```c++ void Tree::insert(int &x,int w) { if(x==0) { x=New(w); return; } if(w<a[x].val) insert(a[x].l,w); else if(w==a[x].val) a[x].cnt++; else insert(a[x].r,w); update(x); if(!check(x)) rebuild(x);} ``` 删除时，由于我们会对树进行重构，且替罪羊树不支持旋转，我们直接把这个要删除的结点的 $cnt$​​ 减去 $1$ 就不管了。 这就是所谓的**懒惰删除法**。 ```c++ void Tree::erase(int &x,int w) { if(w==a[x].val) { a[x].cnt--, update(x); if(!check(x)) rebuild(x); } else { if(w<a[x].val) erase(a[x].l,w); else erase(a[x].r,w); update(x); if(!check(x)) rebuild(x); }} ``` - 查值、查排名 与别的平衡树相仿。其中这个 $res$ 是给查前驱、后继用的。 ```c++ int Tree::getrank(int x,int w) { if(x==0) return 1; if(w<a[x].val) return getrank(a[x].l,w); if(w==a[x].val) { res=a[x].cnt; return a[a[x].l].siz+1; } return a[a[x].l].siz+a[x].cnt+getrank(a[x].r,w); } int Tree::getval(int x,int w) { if(x==0) return 0; if(w<=a[a[x].l].siz) return getval(a[x].l,w); if(w<=a[a[x].l].siz+a[x].cnt) return a[x].val; return getval(a[x].r,w-a[a[x].l].siz-a[x].cnt); } ``` - 查前驱、后继**（难点）** 由于替罪羊树中很多结点实际上并不存在，我们不采用像 *Treap* 那样的查法，而是依赖查值、查排名实现一个前驱、后继。 前面的这个 $res$ 表示有几个相同的值。 ```c++ int Tree::getprev(int x) { int now=getrank(T.rt,x); printf("%d\n",getval(T.rt,now-1)); } int Tree::getnext(int x) { int now=getrank(T.rt,x); res=0; printf("%d\n",getval(T.rt,now+res)); } ``` ### 4. 例题 - [P3369 【模板】普通平衡树](https://www.luogu.com.cn/problem/P3369) 同上，将代码拼起来即为答案。 [Code](https://www.luogu.com.cn/record/53840386) - [P3224 [HNOI2012]永无乡](https://www.luogu.com.cn/problem/P3224) （当然用 *Treap* 也能写） 大力启发式合并搞搞搞就行了！ 发现每个数最多被操作 $\log n$ 次，总复杂度 $\Theta(n\log^2 n)$。 [Code](https://www.luogu.com.cn/record/53903263) - [P5338 [TJOI2019]甲苯先生的滚榜](https://www.luogu.com.cn/problem/P5338) 首先骂一下出题人这个 sb 读入方式，数据又不大为什么要自己生成数据/yun。 然后，如果你用上文提到的 $\alpha=0.75$ 的替罪羊树，是会 T 飞的。 输出一下重构的次数，发现数据大时重构的总 $siz$ 会指数级上升，**因此，我们调大这个 $\alpha$**。 事实上，我把这个 $\alpha$​ 调到 $0.95$​，它就莫名其妙地 AC 了，窝也不知道为什么/kel [Code](https://www.luogu.com.cn/record/53931887) - 一道在知乎上看到的题 > **题意简述**：给定数列 $a$，长度为 $n$。现有 $m$​ 次操作，分为两种： > > 1. 在任意位置插入或删除一个数。 > 2. 求满足 $x\in [l,r]$，且 $a_x\in [u,v]$ 的 $x$ 的个数。 > > $1\leq n,m\leq 10^5$，$1\leq a_i\leq 10^5$。 一种方法当然是用**块状链表**，这里不讨论。 另一种方法是用**树套树**。那么用什么树套什么树呢？ 我们发现，由于有任意位置动态插入、删除的存在，那么外层树肯定不能是线段树，得是平衡树； 而由于内层树只需要支持单点插入、前缀查询，可以直接用 *BIT* 啥的，这里不展开。 但是，外面这棵平衡树又不能是 *Treap* 这种带旋转的，因为旋转之后我们很难由左右子节点的内层树直接合并得到父节点的内层树。 一种做法是把内层树换为红黑树，但我不会打/kel 另一种则比较简单，使用替罪羊树作为外层树，失衡则重构。总复杂度 $\Theta(n\log^2 n)$。 （我是口胡怪/cy） 完结撒花~~