调和点列与极点极线
Diaоsi
·
·
个人记录
1.前置知识
1.1 \mathcal{Apollonius} 圆
定义 :平面内到两个定点的距离之比等于两不等的已知线段之比,则该点轨迹是一个圆,称为 \mathcal{Apollonius} 圆。
证明:因为 \dfrac{PA}{PB}=\dfrac{AM}{BM} ,所以 PM 平分 \angle APB.
同理,PN 平分 \angle APB 外角,\angle NPM=90^\circ,所以P点轨迹为圆。
1.2 \mathcal{Menelaus} 定理及其逆定理
定义 (\mathcal{Menelaus} 定理 ) :若一条直线 l 与 \triangle ABC 的三边 AB,BC,AC 所在的直线交于 D,E,F 三点,则有:
\dfrac{AD}{DB}\cdot\dfrac{BE}{EC}\cdot\dfrac{CF}{FA}=1
证明:作 AG//DE,BE\cap AG =G.
由平行得:\dfrac{AD}{DB}=\dfrac{EG}{BE},\dfrac{CF}{FA}=\dfrac{CE}{EG}
所以:\dfrac{AD}{DB}\cdot\dfrac{BE}{EC}\cdot\dfrac{CF}{FA}=\dfrac{EG}{BE}\cdot\dfrac{BE}{EC}\cdot\dfrac{CE}{EG}=1.
定义 (\mathcal{Menelaus} 逆定理 ) :若 \triangle ABC 的三边 AB,BC,AC 所在的直线上分别存在一点 D,E,F 满足:
\dfrac{AD}{DB}\cdot\dfrac{BE}{EC}\cdot\dfrac{CF}{FA}=1
则 D,E,F 三点共线。
证明略
1.3 \mathcal{Ceva} 定理及其逆定理
定义 (\mathcal{Ceva} 定理 ) :\triangle ABC 内任意一点 P,直线 PA,PB,PC 分别与 BC,AC,AB 交于点 D,E,F,则:
\dfrac{AF}{FB}\cdot\dfrac{BD}{DC}\cdot\dfrac{CE}{EA}=1
证明:对 \triangle ABD,由 \mathcal{Menelaus} 定理可得:
两式相除可得:$\dfrac{AF}{FB}\cdot\dfrac{BD}{DC}\cdot\dfrac{CE}{EA}=1$.。
------------
**定义** **$(\mathcal{Ceva}$ 逆定理 $)$** :若 $D,E,F$ 分别在 $\triangle ABC$ 的边 $BC,AC,AB$ 所在的直线上,并且:
$$\dfrac{AF}{FB}\cdot\dfrac{BD}{DC}\cdot\dfrac{CE}{EA}=1$$
则 $AD,BE,CF$ 相交于一点。
**证明略**
------------
## 2.射影几何基础知识
### 2.1 射影平面基本概念
**定义** 无穷远点:考虑平面上直线与点的对应关系,经过点 $P$ 的直线 $l_1$ 与直线上的点 $A$ 对应,经过点 $P$ 的直线 $l_2$ 与直线上的点 $B$ 对应。
若经过点 $P$ 的直线 $m$ 与直线 $l$ 平行时,在直线 $l$ 上没有任何点与直线 $m$ 对应。为此,在射影几何中引入无穷远点,即直线 $l$ 经过无穷远点并且与直线 $m$ 对应。
在射影几何中,关于无穷远点有以下重要结论:
>1. 平行直线都相交,且交点在无穷远点;
>2. 一条直线只对应一个无穷远点。
------------
**定义** 无穷远直线:在射影几何中,不同的不平行直线对应的无穷远点是不同的,这些无穷远点构成一条直线,称为无穷远直线。
在射影几何中,关于无穷远直线有以下重要结论:
>1. 平面上任意两条直线有且仅有一个交点,其中两条平行直线相交于无穷远点;
>2. 平面上任何无穷远点均在无穷远直线上,无穷远直线上的点均为无穷远点;
>3. 每一个平面上有且仅有一条无穷远直线。
------------
**定义** 射影直线:在欧式平面中,对于一条直线添加无穷远点,则这条直线称为射影直线。
在射影几何中,关于射影直线有以下重要结论:
>1. 射影直线是封闭的;
>2. 任意两条射影直线都相交于一点。
------------
**定义** 射影平面:在欧式平面中,对于每一条直线都添加对应无穷远点,则此平面中添加一条对应无穷远直线,此时组成的平面称为射影平面。
**在射影平面中,任意一条直线都不能将射影平面分成两个部分。**
------------
### 2.2 点列与线束
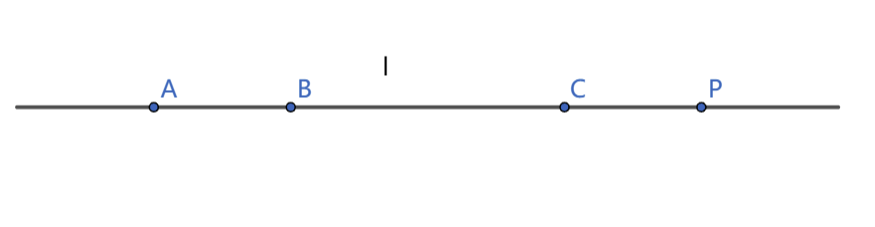
**定义** 点列:同一条直线上的点的集合,记为:$l(A,B,C,\dots)$ 或 $l(P)$。
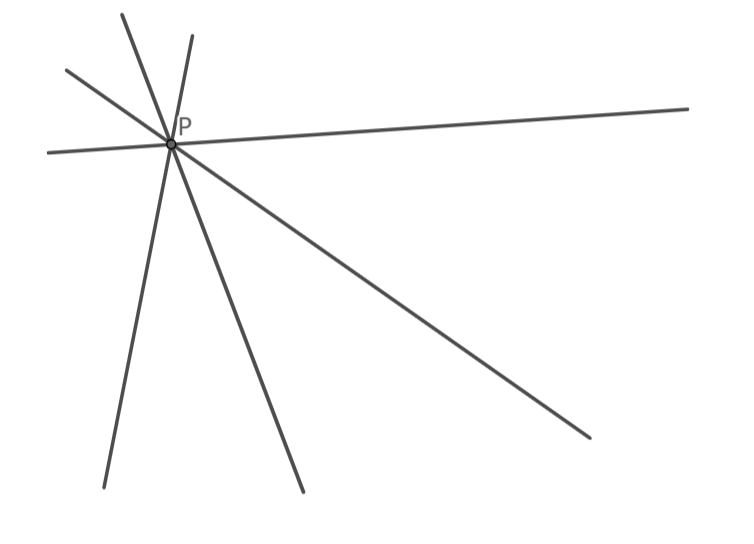
**定义** 线束:平面上过同一点 $P$ 的直线的集合,记为:$P(a,b,c,\dots)$ 或 $P(l)$。
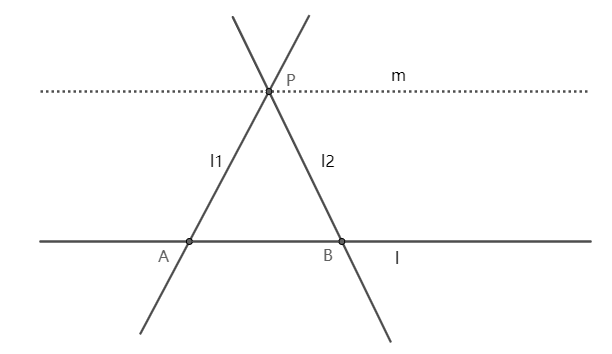
**定义** 中心射影:给定平面上的两直线 $l_1,l_2$ 以及不在 $l_1,l_2$ 上的任意一点 $P$,通过点 $P$ 的直线与 $l_1,l_2$ 交于 $M,N$ 两点,则直线 $l_1$ 上的点与 $l_2$ 上的点便建立起了一一对应关系,该对应关系成为两条直线 $l_1,l_2$ 之间的中心射影(透视对应)。经过点 $P$ 的直线叫做投影线,点 $P$ 叫做投影中心。
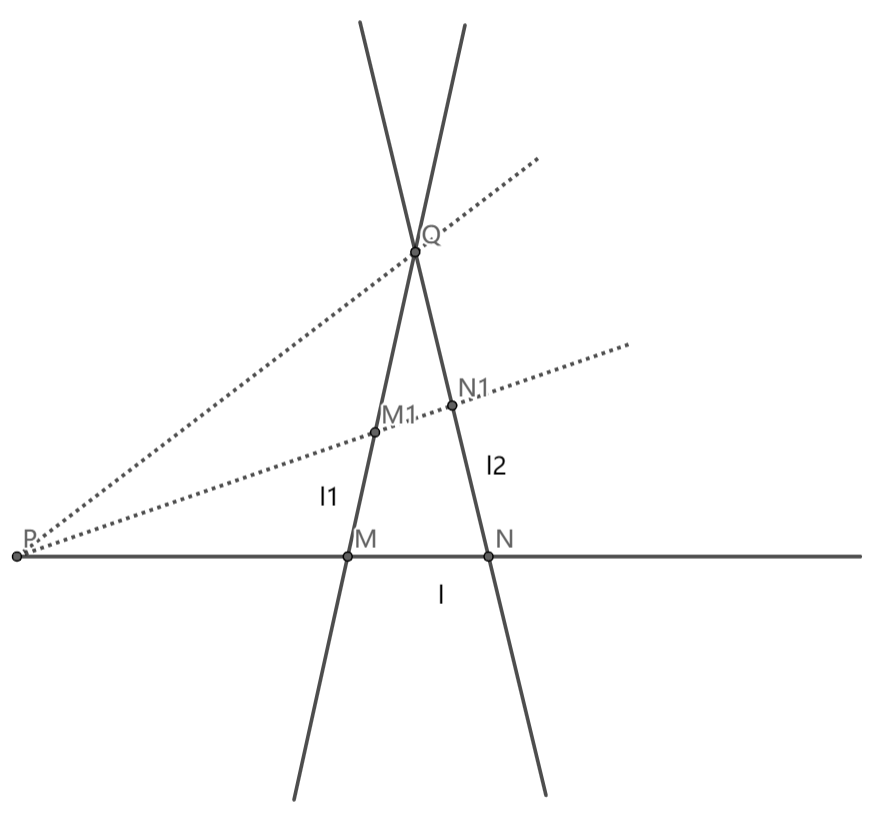
此时点 $N$ 为点 $M$ 关于透视中心 $P$ 的对应点,则点 $Q$ 的对应点是 $Q$,因此称点 $Q$ 为自对应点。
**容易发现**,点列 $l_1(M,M_1,Q)$ 与点列 $l_2(N,N_1,Q)$ 关于点 $P$ 透视对应。
------------