组合数学
Double_Light
·
·
个人记录
组合数
计算方法 $1$:$O(n)$ 递推处理阶乘和阶乘的逆, $\dbinom nm=\dfrac{n!}{m!(n-m)!}$。
计算方法 $2$:$\dbinom nm=\dbinom{n-1}{m-1}+\dbinom{n-1}{m}$。
公式:
规定 $\dbinom{n}{0}=\dbinom{0}{0}=0^0=1$。
$\dbinom{n}{m}=\dbinom{n}{n-m}$。
## 组合意义
比较吃数学直觉,考虑式子在组合学上的意义。
接下来让我们进入小学奥数部分,直观感受组合意义。
### 插板法
有 $n$ 个球,$m$ 个盒子。
1. 球是相同的,盒子是不同的,不许空盒,求方案数。
答案:$\dbinom{n-1}{m-1}$。
不妨把 $n$ 个球排成一列,发现球之间有 $n-1$ 个空格。考虑往空格中插 $m-1$ 个板子(一个空最多插一个板子),把球分成了 $m$ 个连续段,每一段可以看作一个盒子。
2. 球相同,盒子不同,可以空盒,求方案数。
答案:$\dbinom{n+m-1}{m-1}$。
我们额外加 $m$ 个球,把这些每个球往每个盒子中塞一个,保证了不空盒,于是转化为问题 $1$。
### 例题 $\mathbf{1}$:[[ARC110D] Binomial Coefficient is Fun](https://www.luogu.com.cn/problem/AT_arc110_d)
我们转化题意。什么是 $\Pi\dbinom{B_i}{A_i}$?
有 $n$ 组球,中间有 $n-1$ 个挡板。第 $i$ 组有 $A_i$ 个黑球。接下来我们在每一组加上总数不超过 $m-\sum A_i$ 个白球的方案数。
现在我们加入第 $n+1$ 组。假设我们要在前 $n$ 组放入 $x$ 个白球,那么剩余的 $m-\sum A_i-x$ 个球将被放在 $n+1$ 组。
现在我们把问题转化为:在 $\sum A_i$ 个球和 $n$ 个隔板中插入 $m-\sum A_i$ 个球,求总方案数。
也就是 $n+m$ 个元素中选 $m-\sum A_i$ 个。所以答案为 $\dbinom{n+m}{m-\sum A_i}$。
$m-\sum A_i$ 的值较大,于是转化成 $\dbinom{n+m}{n+\sum A_i}$ 进行计算。
### 例题 $\mathbf{2}$:[CF1204E - Natasha, Sasha and the Prefix Sums](https://www.luogu.com.cn/problem/CF1204E)
令 $g_i$ 表示有多少方案最大前缀和 $=i$,答案就是 $\sum g_i$。
直接求 $g_i$ 是困难的。令 $f_i$ 表示有多少方案最大前缀和 $\geq i$,然后用差分就可以求出 $g_i$。
接下来求 $f_i$。
构造二维序列 $(x,y)$ 的第一维表示当前的下标,第二维表示当前的前缀和。
问题转化成:从 $(0,0)$ 走到 $(n+m,n-m)$,每次可以向右上和右下方走。求有多少种方案满足路径与直线 $y=i$ 有交点。答案就是 $f_i$。
分类讨论:
- 当 $n-m\geq i$ 时:
因为 $0\leq i\leq n-m$,所以一定有交,答案就是 $\dbinom{n+m}{n}$,也就是 $n+m$ 步选 $n$ 步向上走。
- 而当 $n-m<i$ 时:
假设某种方案满足条件,那么一定可以找到第一个与 $y=i$ 的交点,设其为 $(x,i)$,那么我们把 $[0,x]$ 的图象沿着 $y=i$ 翻折上去,就转化为了第一种情况,起点是 $(0,2i)$,终点是 $(n+m,n-m)$。
偷一下题解的图:
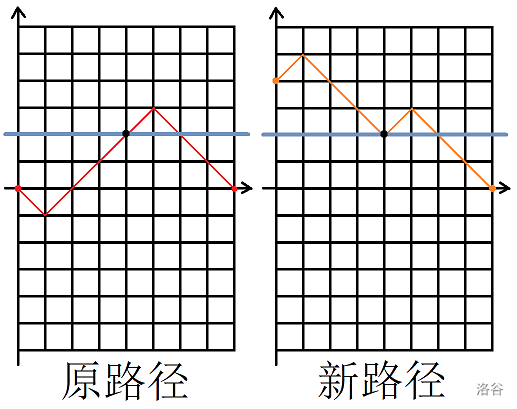
并且每一条起点是 $(0,2i)$,终点是 $(n+m,n-m)$ 的路径都会与 $y=i$ 有至少一个交点,将第一个这样的交点左侧的图象翻折下去,又可以得到一条 $(0,0)\to(n+m,n-m)$ 的路径,于是 $(0,0)\to(n+m,n-m)$ 与 $y=i$ 有交的路径与 $(0,2i)\to(n+m,n-m)$ 的路径一一对应。
那么转化为情况 $1$,直接计算 $(0,2i)\to(n+m,n-m)$ 的路径总数即可。
答案为 $\dbinom{n+m}{i+m}$。
### 补充:卡特兰数与一个路径计数问题
考虑如下问题:求平面直角坐标系中从 $(0,0)$ 走到 $(n,n)$ 且始终在第一象限的角平分线下方(或在角平分线上)的路径条数。
对于一条合法的路径而言,显然必须经过 $(1,0)$ 和 $(n,n-1)$。所以我们统计经过这两点的路径总数减去经过这两点的不合法路径数量。
路径总数显然是 $\dbinom {2n}n$。接下来考虑统计不合法路径。
假设路径不合法,那么必然存在至少一个与 $y=x$ 的交点。我们把这个交点左侧的路径图象关于 $y=x$ 做对称,发现新得到的路径一定经过 $(0,1)$ 和 $(n,n-1)$。与上题类似的证明可以得到分别以 $(0,1)$ 和 $(n,n-1)$ 为起点和终点的路径与统计的不合法路径一一对应。于是不合法路径数量为 $\dbinom{2n}{n-1}$。
所以问题的答案为 $\dbinom {2n}n-\dbinom{2n}{n-1}$,这正是卡特兰数的通项公式 $H_n$。
## 二项式与式子推导
### 二项式定理
狭义的形式:
对于 $\forall k\in\mathbb{N^+},(x+y)^k=\sum_{i=0}^kx^iy^{k-i}\dbinom ki$。
推论 $1$:$(1+1)^k=\sum_{i=0}^k\dbinom ki=2^k$。
推论 $2$:$(1-1)^k=\sum_{i=0}^k(-1)^i\dbinom ki=[k=0]$。
推论 $3$:$(x+1)^k=\sum_{i=0}^kx^i\dbinom ki$。
### 一些推导简单的常见恒等式
1. $\sum_{k=0}^n\dbinom km =\dbinom{n+1}{m+1}$。
证明:按照组合数的递推公式展开右式。
2. $\sum_{k=0}^n\dbinom {m+k}k=\dbinom{m+n+1}n$。
证明:展开右式。
3. $\sum_{k=1}^nk\dbinom nk=n\times2^{n-1}$。
证明:$k\dbinom nk=\dfrac{n!}{(k-1)!(n-k)!}=n\dbinom{n-1}{k-1}$。
于是得到 $\sum_{k=1}^nk\dbinom nk=n\sum_{k=0}^{n-1}\dbinom{n-1}{k}=n\times2^{k-1}$。
4. $\sum_{i=0}^n\dbinom ai\dbinom b{n-i}=\dbinom{a+b}n$。
证明:组合意义显然。
5. $\sum_{i=0}^m\dbinom ni\dbinom mi=\dbinom{n+m}m$。
证明:$\dbinom mi=\dbinom m{m-i}$,然后由 $4$ 得。
6. $\dbinom nm\dbinom mk=\dbinom nk\dbinom{n-k}{m-k}$。
证明:组合意义,左边代表先在 $n$ 个元素种选 $m$ 个再从 $m$ 个中选出 $k$ 个,右边代表直接选 $k$ 个,然后从剩下的 $n-k$ 里面选出剩下的 $m-k$ 个。
### 广义二项式
修改组合数的定义:$\dbinom{n}{m}=\dfrac{n(n-1)(n-2)\dots(n-m+1)}{m!}$。
这样就可以把 $n$ 扩展到实数集,上面式子的大部分也是成立的。
由此我们在广义二项式下有
上指标反转:$\dbinom nm=(-1)^m\dbinom{m-n-1}m$。
证明:带入定义式即可。
### 一些有意思的式子
1. 推和式
$(1) \sum_{i=m}^n(-1)^i\dbinom ni\dbinom im=(-1)^m[n=m]$。
证明:
$$\sum_{i=m}^n(-1)^i\dbinom ni\dbinom im$$
$$=\sum_{i=m}n(-1)^i\dbinom nm \dbinom{n-m}{i-m}$$
$$=\dbinom nm\sum_{i=0}^{n-m}(-1)^{i+m}\dbinom{n-m}i$$
$$=(-1)^m\dbinom nm\sum_{i=0}^{n-m}\dbinom{m-n-1+i}i$$
$$=(-1)^m\dbinom nm\dbinom 0{n-m}=[n=m](-1)^m$$
$(2) \sum_k\dbinom{n+k}{2k}\dbinom{2k}k\dfrac{(-1)^k}{k+1}=[n=0]$。
证明:
$$\sum_k\dbinom{n+k}{2k}\dbinom{2k}k\dfrac{(-1)^k}{k+1}$$
$$=\sum_k\dbinom{n+k}{k}\dbinom{n}k\dfrac{(-1)^k}{k+1}$$
$$=\dfrac{1}{n+1}\sum_k\dbinom{n+k}k\dbinom{n+1}{k+1} (-1)^k$$
$$=\dfrac{1}{n+1}\sum_k\dbinom{n+k}k\dbinom{n+1}{k+1}(-1)^k$$
$$=\dfrac{1}{n+1}\sum_k\dbinom{-n-1}k\dbinom{n+1}{k+1}$$
$$=\dfrac{1}{n+1}\dbinom{0}{n}=[n=0]$$
## 容斥原理
### 一个简单的例子
有三个集合 $S_1,S_2,S_3$,求 $|S1\cup S_2\cup S_3|$。
显然答案为 $|S_1|+|S_2|+|S_3|-|S_1\cap S_2|-|S_1\cap S_3|-|S_2\cap S_3|+|S_1\cap S_2\cap S_3|$。
这是大小为 $3$ 的容斥原理的情况。
### 通用公式
$$|\bigcup_{i=1}^n S_i|=\sum_{k=1}^n(-1)^{k+1}\sum_{p_1<p_2<\dots<p_k}|S_{p_1}\cap S_{p_2}\cap\dots\cap S_{p_k}|$$
证明:对每个元素 $x$ 计算贡献。
### 例题 $\mathbf{3}$:[[HAOI2008] 硬币购物](https://www.luogu.com.cn/problem/P1450)
首先考虑没有硬币数量限制的做法。直接进行完全背包预处理然后输出就可以。
后面你先别急。