易懂科技：将LCA、RMQ、LA优化至理论最优复杂度

## 前言 LCA、RMQ、LA(树上 K 级祖先)是三类经典问题，但这三类的的经典/常用解法并非理论最优复杂度。 然鹅有一种简单的思想，即 $\texttt{Method of Four Russians}$ ，可以同时将这三种算法优化至理论最优复杂度。 下文作者将对三种问题进行简单介绍，并详细解释此思想、以及如何用于解决这三类问题，并提供了笔者的代码实现，还附赠对于此算法解决 LCA 的[小优化](https://www.luogu.com.cn/paste/8vpwhz75)，并增补对 RMQ 的优化和对 LCA 的再优化。 ## 问题介绍 由于都是经典问题及解法，默认以下问题及算法读者有所掌握，不会的话左转模板区看看。 1. LCA(Lowest Common Ancestor)，最近公共祖先，求树上两点的祖先中深度最大的一个，是一类广为人知经典问题。 在这里用 $O(A)-O(B)$ 分别表示预处理复杂度和询问复杂度。 常见算法有 $O(n\log{n})-O(\log{n})$ 的倍增算法、$O(n)-O(\log{n})$ 的树剖算法、$O(n)-O(\sqrt{n})$ 的长链剖分算法、$O(n\log{n})-O(1)$的欧拉环游序+普通 RMQ 算法等。 由于一棵树为 $O(n)$，理论最优复杂度应为 $O(n)-O(1)$。 2. RMQ(Range Maximum/Minimum Query)，区间最值问题，求序列一个区间中的最大/最小，也是一类广为人知经典问题。 常见算法有 $O(n\log{n})-O(1)$ 的 ST 算法、$O(n)-O(\log{n})$ 的线段树/树状数组算法、$O(n)-O(\sqrt{n})$ 的暴力根号分块算法等。 由于一个序列为 $O(n)$，理论最优复杂度同样应为 $O(n)-O(1)$。 3. LA(Level Ancestor)，树上 K 级祖先，求树上某点的第 K 级祖先，也算容易实现的经典问题了。 常见算法有 $O(n\log{n})-O(\log{n})$ 的倍增算法、$O(n)-O(\log{n})$的树剖算法(当然询问可以做到比较奇怪的复杂度，如 $O(\log{\log{n}}/\sqrt{\log{n}})$ 等)、$O(n\log{n})-O(1)$ 的长剖算法等。 一棵树为 $O(n)$，显然理论最优复杂度仍应为 $O(n)-O(1)$。 部分常见算法由于与此算法无关，故下文不作介绍。 ## 思想引入 $\texttt{Method of Four Russians}$ 的前置思想为 **分块** 。 而其核心在于对块间和块内 **分别** 解决问题以达到更优的复杂度。 我们先来玩一下分块：(如果你对分块有足够的了解， **请跳至下一个标题** ) 尝试直接用分块思想优化 RMQ。(你也可以大概看看思想，反正都~~是乱搞~~会优化失败的) 从 RMQ 中的暴力分块算法看起，我们将序列分为 $\sqrt{n}$ 块，预处理每块的最值，询问时遍历边角块与整块取最值。 对于 RMQ 问题，我们发现次算法复杂度相较并不优秀，但我们通过思考可以发现遍历取最值可以预处理优化，即根号分块套暴力或 ST 算法。 记 $T=(\sqrt{n}\log{\sqrt{n}}/(\sqrt{n})^2)$，复杂度为 $O(T+T\sqrt{n})-O(1)$。 具体分析：块间整体一次可以选择暴力处理或套用 ST 算法，复杂度即 $T$，同时有 $\sqrt{n}$ 个小块，每个块内一次也有同样的选择，询问均为 $O(1)$。 我们发现这个花里胡哨的复杂度仍为 $O(T\sqrt{n})=O(n\log{n}/n\sqrt{n})$，但我们显然可以感觉出来是块的大小不平衡导致的，于是我们尝试调整块的大小，然后将块的大小调为 $n/1$ 的块后发现调回了 ST 算法/暴力。。。 ## Method of Four Russians 虽然对于 RMQ 问题这样优化是没有出路的，但我们已经对分块优化算法的这种方法有所了解。 在这里分块失败的原因一个是由于问题本身不能直接用分块最优化，即没有**合适**的算法来套用。还有个原因是因为块间和块内的算法**相同**，最后就会导致分成了一个块。 于是 $\texttt{Method of Four Russians}$ 就出来给我们提供了更完美的分块思路： 将集合大小为 $n$ 问题分为大小为 $B$ 的 $\frac{n}{B}$ 个块，$B$ 通常取 $c\log{n}$，$c$ 为一个常数，且通常不超过 1。 然后对于所有大小为 $B$ 的小块(理性理解一下这个块其实特别小)整体套用一个 $O(B\log{B})$ 的算法，对于小块内部套用 $O(x^{c\log{n}} ⋅ y)$ 的算法。 这里块间的算法通常使用原算法，而块内算法为暴力算法，同时使得所有 $\frac{n}{B}$ 个块都属于已处理的集合 $x^{c\log{n}}$。这里 $x$ 为一个常数，前面 $y$ 为某个算法的复杂度。 ## 对 LCA 的优化 对于 LCA 问题，我们已有较优秀的算法 欧拉环游序+ST 来求 LCA。(算是经典操作了吧，网上随便都有) 我们先求出这棵树的欧拉环游序，考虑在此基础用 $\texttt{Method of Four Russians}$ 进行优化。 一个完整的欧拉环游序有个优(qi)秀(guai)的性质：相邻两点的深度差为 1。事实上用的并不多，有的人为了追求更优的复杂度可以将欧拉环游序缩减为一半，但却破坏了此性质。 我们将这个序列(长度设为 $n$)分为长为 $l=\frac{\log{n}}{2}$ 的块，对于块间直接上原算法 ST，设 $k=\dfrac{n}{\frac{\log{n}}{2}}=\frac{2n}{\log{n}}$，复杂度为 $O(k\log{k})=O(n)$。 对于块内，我们要利用上面的性质，求出每一个小块的**深度的**差分序列，于是有每个差分序列仅由 $\text{1，-1}$ 构成。 又由于长度仅为 $l=\frac{\log{n}}{2}$ ，故本质不同的差分序列只有 $2^{l-1}=O((2^{\log{n}})^{\frac{1}{2}})=O(\sqrt{n})$ 个。 对于每个差分序列，将首项置为 0 还原出一个序列，对其预处理 RMQ，复杂度为 $O(\sqrt{n} * (l^2/l\log{l}))<O(n)$，这里可以直接暴力处理区间，如果你够闲你可以对小块也做 ST。 询问时就按分块的方法询问，对于块间有 ST 表，对于块内可以找到对应的差分序列询问前后缀，此处的前后缀也可以不用差分序列，直接遍历 $O(n)$ 预处理也能做到 $O(1)$ 询问(常数还小)。 但特别地，有两点处于同一小块中的情况，还是找到对应的差分序列询问区内，这也是预处理小块的意义所在。 由于这是第一个讲解的问题，有点抽象，我们来看点栗子。~~听说没有图不让过？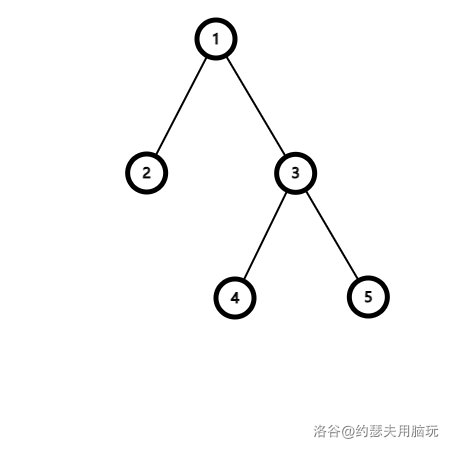~~  欧拉环游序为：$1\ 2\ 1\ 3\ 4\ 3\ 5\ 3\ 1$。 令块的大小 $l=3$，有 $1\ 2\ 1|3\ 4\ 3|5\ 3\ 1$，第一块深度最小为 1 号点，同理第二块为 3 号点， 第三块为 1 号点，区间询问的话取最小就是了。 考虑块内，(深度)差分序列分别为 $\text{1\ -1\ |\ 1\ -1\ |\ -1\ -1}$。 对 $\text{1\ -1}$ 来说，还原后为 $0\ 1\ 0$，最小位置的数组为： $mn[\text{-1,1}][i][j]$ 表示这种序列 $i\sim j$ 区间的最小位置：$\begin{bmatrix}1&1&1\\/&2&3\\/&/&3\end{bmatrix}$ 对 $\text{-1\ -1}$ 来说，还原后为 $\text{0\ -1\ -2}$，最小位置的数组为： $mn[\text{-1,-1}][i][j]$ 表示这种序列 $i\sim j$ 区间的最小位置：$\begin{bmatrix}1&2&3\\/&2&3\\/&/&3\end{bmatrix}$ 若询问 2、5 的LCA，在第一块 $\text{1\ -1}$ 中查询区间 $(2,3)$，找到第三个位置，对应节点 1，第二块直接取 3，第三块查询区间 $(1,1)$，找到第一个位置，对应节点 5，对以上三个取最小，答案为 1 号节点。 若询问 4、4 的LCA，在第二块中查询区间 $(2,2)$，对应节点 4。 [代码实现(仅供参考)](https://www.luogu.com.cn/paste/p8o83rum) ## 对于 RMQ 的优化 ~~你不是说不能优化 RMQ 的吗~~ 咳咳，虽然不能直接优化 RMQ，但我们可以用[笛卡尔树(含简单解释)](https://www.luogu.com.cn/paste/3ebe61r2)将区间 $(l,r)$ 转化为树上 $l,r$ 对应两点 LCA 的问题，就可以直接套用上面的 LCA 优化了。 由于利用了相邻两点的深度差为 1 的性质，故也有人称其为 $\pm 1$ RMQ 或是约束 RMQ。(听听就好) [代码实现(仅供参考)](https://www.luogu.com.cn/paste/8j9b4mz5) ## 对于 LA 的优化 我们已有一种较优秀的算法 长剖+倍增数组($O(n\log{n})-O(1)$) 来求 LA。(长剖经典应用，不会的去请先学长剖) (不是我不想讲，是真没什么讲的 $=\ \ =$ ,上面的欧拉环游序也是) 考虑一个简单的优化：对于每个点预处理出任意一个子树中的叶子节点以及距离(设为 $d$)，显然可以 $O(n)$ 做到，于是我们将一个点的 K 级祖先转化为一个叶子的 $K+d$ 级祖先，故只用对所有叶子节点做倍增数组 $O(L\log{n})$。 由于叶子数 $L$ 可能为 $O(n)$，故最坏复杂度仍为 $O(L\log{n})=O(n\log{n})$。 考虑在此基础上用 $\texttt{Method of Four Russians}$。 我们将靠近叶子的点删掉，得到一棵新树。更具体地，我们将原树上子树不超过 $B=\frac{\log{n}}{4}$ 的节点删去，于是有新树的叶子节点数不超过 $\frac{n}{B}$，因为他们在原树中的子树均超过了 $B$ 。 考虑询问点在新树上，套用之前的叶子节点 $K+d$ 级祖先算法，有复杂度 $k=\frac{n}{B},O(k\log{n})-O(1)$。 考虑询问点为被删除的点，可以发现所有被删的节点构成了每棵树大小不超过 $B$ 的森林。 还是预处理到新树的叶子节点的距离 $d$，若有 $K\ge d$，那么转化为新树上叶子节点的 $K-d$ 级祖先，$O(n)$ 预处理然后套上面的询问即可。 否则与新树无关，且森林间每棵树独立，以下将被删树的大小看做 $B$。 考虑被删树种类的可能性，如果你对 Catalan 数比较熟悉的话可以直接报出有 $\dfrac{C_{2B}^{B}}{B+1}$ 种(这就是 Catalan 数，如果你知道多叉树可以转化为二叉树的话会更容易看出来)。 我们考虑得到一棵树的括号序列，即进入一个子树时加前括号，退出时加后括号，$B$ 对括号的方案数即为 Catalan 数。[Catalan 的简单解释](https://www.luogu.com.cn/paste/f5rxugmn) 反之，如果我们有一个括号序列我们可以反推出这棵树，对于每种树(也及每种括号序列)暴力处理 K(有$K\le d$) 级祖先即可，复杂度 $O(\dfrac{C_{2B}^{B}}{B+1} * B^2(/B\log{B}))=O(4^B * B^2)=O(\sqrt{n}\log^2{n})<O(n)$。(当然你可以闲到对每种树写长剖) 也就是我们对于每种被删树，取出它的括号序列，通过预处理的直接 $O(1)$ 询问即可。你会发现这个和上面 LCA 的差分序列处理(思路)十分相似，可以参考代码以便理解。 询问的方法在上面已经讲解过就不再赘述。 [代码实现(仅供参考)](https://www.luogu.com.cn/paste/mge9d7x9) ## LCA 的另一种优化 上文的 LCA 优化中，块间的复杂度为 $k=\dfrac{n}{\frac{\log{n}}{2}}=\frac{2n}{\log{n}},O(k\log{k})=O(n)$ ，实则 $k\log{k}$ 大于 $n$，故此算法预处理的瓶颈在这里。 考虑调整块的大小 $l=\log{n}$，则本质不同的小块数变为 $2^{l-1}=O(2^{\log{n}})=O(n)$ (略小于 $n$)个。 但注意到其优秀的性质，我们将差分序列中的 1 看作 0，-1 看作 1，即对应为一个 01 序列，其最小值可以由比它去掉最高位(即最大的一个 1)后的 01 序列 $O(1)$ 转移过来，故小块复杂度仍为 $O(n)$。 若询问一个差分序列的区间，用位运算直接取出对应的 01 序列，末尾空位用 0 补齐 $l-1$ ，就可以直接由预处理过的 01 序列得到，故询问小块依旧为 $O(1)$。 且显然有块间复杂度 $k=\dfrac{n}{\log{n}},O(k\log{k})=O(n)$ (也略小于 $n$)。 复杂度瓶颈优化为更严格的 $O(n)$，但也仅为理论常数上的优化。 [代码实现](https://www.luogu.com.cn/paste/s2yxw3fk) ## RMQ 的另一种优化 之前笔者由于太累(lan)了，没有阐述他人提出的更好的 idea，故在此增补一下。其实其他优化与上文都有异曲同工之妙，不比上文困难，还是值得一看。 LCA 的另优化给了我们启发，我们并不用像 LCA 初优化中的暴力那样，将每一种状态的每一个情况处理出来。我们只关心我们需要的，故我们只快速地预处理了差分序列最小位置，达到了优化的目的。 我们再来看 RMQ，我们发现像之前那样显示地将笛卡尔树建立出来再求 LCA 十分地冗余，感觉绕了一大圈才回到原问题。 考虑在这里建立笛卡尔树的本质，其实是使起点固定的单调栈得以区间询问。 先将块的大小设为 $l=\log{n}$，对于块间还是使用原算法 ST ，而对于块间维护一个单调栈。 显然可以发现，对于区间 $(l,r)$ 的最大值即为最后一个为 $r$ 的单调栈中位置大于 $l$ 的第一个位置的值。 借用一个例子： 对于序列 $a:1\ 3\ 5\ 2\ 4$ 维护单调栈(以下为位置的编号)： $1:1$ $2:2$ $3:3$ $4:3\ 4$ $5:3\ 5$ 询问区间 $(2,4)$ 中的最大值，就为第 4 个单调栈中比位置 2 大的第一个位置 3，位置 3 的值为 5，即为区间最大。 于是我们只用对于每个末尾用 01 序列存下其单调栈的出现情况，查询时同样运用刚刚 LCA 的用的技巧，用位运算取出对应 01 序列直接由预处理得到答案。 由于没有建笛卡尔树和欧拉环游序，序列长度为 $n$，在块取 $l=\log{n}$ 时是特别标准的 $O(n)-O(1)$ 复杂度，理论常数远胜 RMQ 初优化。 [代码实现(仅供参考)](https://www.luogu.com.cn/paste/6n8ujq59) ## LCA 再优化 ~~我会套娃！~~ 注意到我们已经有了一个常数优秀的 $O(n)-O(1)$ RMQ，考虑对优化欧拉环游序。 由于欧拉序列长为 $2n(-2)$ 且我们询问端点只有 $n$ 个，考虑对欧拉序缩起来。 简单来说，欧拉序是边从上往下时加入一次，从下往上又加入一次。 而我们显然发现最后一次从下往上加入的点是不必要的，也就是说每个点返回时我们使其不加入欧拉序查询也显然是对的，而这样就只剩下了 $n-1$ 个点。 虽然失去了其优秀的性质，但我们直接套用另优化 RMQ，常数得以更进一步。 [代码实现(仅供参考)](https://www.luogu.com.cn/paste/rw71gd43) ## 后序 这三类问题的最优复杂度流传的并不广，多数人最多也就听过约束 RMQ 能优化 LCA。个人认为，问题在于算法优势不明显，~~而且卡树剖会被骂~~，笔者希望这些算法能在常数或是码量上有更好的提升，当然也希望大家都能理解这些算法，使它们能有更广泛的应用。~~这样就能出毒瘤卡常题了~~ 如果我有什么错别字、废话或是不清晰的地方可以跟我说。 ## 参考文献 2017IOI国家候选队论文《非常规大小分块算法初探》——徐明宽 [_26535_ 的博客《推广一种常数较小，码量不大的 O(n)-O(1) RMQ》](https://www.luogu.com.cn/blog/2-6-5-3-5/tui-guang-yi-zhong-chang-shuo-jiao-xiao-ma-liang-fou-tai-di-on-o1-rmq) [skip2004 的博客《最近公共祖先》](https://www.cnblogs.com/skip1978/p/12240164.html)