【动态规划 & 树形dp】Tree DP
Fireworks_Rise
·
·
算法·理论
一、简单介绍 (Tree DP)
①、定义状态:根据问题的特点,定义每个节点需要保存的状态。可以是最大值、最小值、累加和、路径长度等等。
②、设计转移方程:根据问题的要求,定义每个节点状态之间的转移关系。这个转移关系通常由树的拓扑结构决定,先在每个节点处定义状态,再利用已经计算出的节点状态来计算当前节点的状态。
③、遍历计算:使用深度优先搜索 (DFS)或广度优先搜索(BFS)遍历整个树,按照定义的转移方程计算每个节点的状态。
④、求解最终结果:根据最终状态的定义,从中选择所需的结果,比如最大值、最小值等。
二、代码实现
树形dp 之 选择节点类
例题引入
题目
洛谷 P1352 没有上司的舞会
描述
某大学有 n 个职员,编号为 1 \ldots n。
他们之间有从属关系,也就是说他们的关系就像一棵以校长为根的树,父结点就是子结点的直接上司。
现在有个周年庆宴会,宴会每邀请来一个职员都会增加一定的快乐指数
所以,请你编程计算,邀请哪些职员可以使快乐指数最大,求最大的快乐指数。
#### 输入格式
输入的第一行是一个整数 $n$ 。
第 2 到第 $(n+1)$ 行,每行一个整数,第 $(i+1)$ 行的整数表示 $i$ 号职员的快乐指数 $r_i$ 。
第 $(n+2)$ 到第 $2n$ 行,每行输入一对整数 $l , k$ ,代表 $k$ 是 $l$ 的直接上司。
#### 输出格式
输出一行一个整数代表最大的快乐指数。
#### 输入/输出样例
##### 输入 #1
```
7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
```
##### 输出 #1
```
5
```
#### 说明/提示
##### 数据规模与约定
对于 $100\%$ 的数据,保证 $1 \le n \le 6×10^3$ , $-128 \le r_i \le 127$ , $1 \le l,k \le n$,且给出的关系一定是一棵树。
-----
## 思路
先浅浅地说说**选择节点类**的一般转移方程:
$\begin{cases}
f_{u,0}=f_{v,1} \\
f_{u,1}=\max/\min(f_{v,0},f_{v,1})
\end{cases}.
选择节点式的题首先前提条件是整个数据是由树形结构存储的,或者应该用树形结构存,运行的效率更高,而且相邻的节点是不能同时存在的,最后要求取最大最小值 。
I.建立树
用链式前向星建树,这里是储存一棵树,所以每两个结点之间只需要建立一条边,即等同于有向无环图。
我们还需要统计每个结点的**入度**,如果当前的结点的**入度为 $0$** ,则此结点必定是这棵树的**根节点**(root)。
### II. dfs 遍历整棵树
借助**链式前项星**遍历整棵树。
此处用一个数组 $f$ 来记录当前子节点的状态。
$f_{u,0}$表示 u 不去
$f_{u,1}$表示 u 去
**状态转移方程**如下:
$\begin{cases}
f_{u,0}+=\max(f_{v,0},f_{v,1}); \\
f_{u,1}+=f_{v,0};
\end{cases}
①. u 不去,那么它的子节点(直接下属)可去可不去,取其最大值即可。
②. u 去了那么它的子节点一定不能去,直接加。
最后找到根节点,ans=\max(f_{root,0},f_{root,1})。
Code
#include<bits/stdc++.h>
using namespace std;
const int N=6001;
int n,h[N],l,k,root;
struct Edge {
int v,nxt;
}edge[N<<1];
int head[N],idx;
int f[N][3],degree[N];
void add(int x,int y) { //邻接表建图
edge[++idx].v=y;
edge[idx].nxt=head[x];
head[x]=idx;
}
void dfs(int u,int fa) { //进行树形dp
f[u][0]=0,f[u][1]=h[u];
for(int i=head[u];i;i=edge[i].nxt) { //遍历当前结点u的子节点v
int v=edge[i].v;
dfs(v,u); //继续向下dfs遍历
f[u][0]+=max(f[v][1],f[v][0]); //父节点由子节点转移过来
f[u][1]+=f[v][0]; //若上司不去,下属可以选择去不去;反之,上司去,下属就不去
}
}
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&h[i]);
for(int i=1;i<n;i++) {
scanf("%d%d",&l,&k);
add(k,l); //有向边构图,有直属关系,
degree[l]++; //记录入度
}
for(int i=1;i<=n;i++) { //寻找根节点
if(degree[i]==0) {
root=i;
break;
}
}
dfs(root,0);
printf("%d\n",max(f[root][0],f[root][1])); //取最大值
return 0;
}
类似的选择节点类的经典例题还有 洛谷 P2016 战略游戏 等
树形dp 之 树的直径类(有些超纲)【图论•算法】
- 树的直径,(Diameter of a Tree),又称树的最长链,定义为一棵树上最远的两个节点的路径,即树上一条不重复经过某一条边的最长的路径。树的直径也可以代指这条路径的长度,树是以邻接表存无向边的形式储存的。
在树上寻找 树的直径(最长链) 的方法:
前提:此做法只有在权值为正数的情况下才能使用。
1). 对于任意一点,假设这个结点为 a ,那么,我们需要找到离 a 最远的结点(如果不在同一棵子树上,通常为叶子结点)x 。
2). 再对 x 结点,继续搜索寻找最远的结点 y .
3). 最后,从 x 出发到 y 结点的整条路径就是这棵树的直径之一。
注意:一棵树的所有直径的长度(边权值总和) 都一样。
对于此处,大家可能会放出疑问,或者你已经理解了,但你只是模糊的明白,还不能很好的证明,本蒟蒻也是学得一脸蒙,最后只能搬大佬的详细证明,再结合自我理解,最通俗地讲述给大家。
F1 证明(反证大法)
假设此树的最长路径是从 s 到 t ,我们选择的点为 u 。
假设搜到的点是 v ,分两种情况讨论。
1、结点 v 在这条最长路径(即树的直径)上,那么 dist_{u,v}>dist_{u,v}+dist_{v,s} ,显然矛盾。
2、结点 v 不在直径上,且 (u,v) 和 (s,t) 有公共点 p,
如图所示:
此时 dist_{u,v} > dist_{v,t}=dist_{u,p} > dist_{t,p} ,
则dist_{u,s}> dist_{s,t}=dist_{u,s}> dist_{u,v} ,此时 (s,t) 不是树的直径,于已知矛盾。
3、节点 v 不在这条最长路径上,即 (s,t) 和 (u,v) 没有公共点,在最长路径上任意选择一个点为 p ,则dist_{u,v}>dist_{u,p}+dist_{p,t} ,那么有 dist_{s,v} \gets dist_{s,p}+dist_{p,u}+dist_{u,v}>dist_{s,p}+dist_{p,t} \to dist_{s,t} ,即 dis_{s,v}>dis_{s,t} ,矛盾。
综上所述,经过两次的 dfs 求出最长路径的两个端点和其的路径长度便是树的直径。
F2 证明(交换论证大法):
!!大佬做法!!
经典模板题 [洛谷转载自SPOJ PT07Z - Longest path in a tree](https://www.luogu.com.cn/problem/SP1437)
### 题目描述
给你一个无权无向的树。编写程序以输出该树中最长路径(从一个节点到另一个节点)的长度。在这种情况下,路径的长度是我们从开始到目的地的遍历边数。
### 输入格式
输入文件的第一行包含一个整数 $N$ ——树中的节点数。
接下来 $N−1$ 行包含该树的 $N−1$ 个边---每行包含一对 $(u,v)$ ,表示在节点 $u$ 和节点 $v$ 之间存在边。
### 输出格式
输出最长路径的长度。
### 输入/输出样例
#### 输入 #1
```
3
1 2
2 3
```
#### 输出 #1
```
2
```
### 说明/提示
对于 $100\%$ 的数据,$1 \le N \le 10^4$ ,$1 \le u,v \le N$ 。
### Code(权值无负,全正)
如果权值**全部**都为**不为负数**,即任意结点 $a_i \geq 0$ ,则可用上述方法,进行**两次** dfs 找出**最远的两个节点**即可。
```cpp
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
int n,x,y;
struct Edge {
int v,nxt;
}edge[N<<1];
int head[N],idx;
int dist[N];
void add(int x,int y) {
e[++idx].v=y;
e[idx].nxt=head[x];
head[x]=idx;
}
void dfs(int u,int step) {
if(dist[u]!=0) return ;
dist[u]=step;
for(int i=head[u];i;i=edge[i].nxt) {
int v=edge[i].v;
dfs(v,step+1);
}
}
int main() {
scanf("%d",&n);
for(int i=1;i<n;i++) {
scanf("%d%d",&x,&y);
add(x,y),add(y,x);
}
dfs(1,1);
int maxx=0,k=0;
for(int i=1;i<=n;i++)
if(dist[i]>maxx) maxx=dis[i],k=i;
memset(dist,0,sizeof(dist));
dfs(k,1);
maxx=0;
for(int i=1;i<=n;i++)
maxx=max(dist[i],maxx);
printf("%d\n",maxx-1);
return 0;
}
```
----
### 题目描述
给定一棵树,树中包含 $n$ 个结点(编号 $1 ∼ n$ )和 $n−1$ 条无向边,每条边都有一个权值。
现在请你找到树中的一条最长路径。
换句话说,要找到一条路径,使得路径两端的点的距离最远。
注意:路径中可以只包含一个点。
### 输入格式
第一行包含整数 $n$。
接下来 $n−1$ 行,每行包含三个整数 $a_i , b_i , c_i$ ,表示点 $a_i$ 和 $b_i$ 之间存在一条权值为 $c_i$ 的边。
### 输出格式
输出一个整数,表示树的最长路径的长度。
### 输入/输出样例
#### 输入 #1
```
6
5 1 6
1 4 5
6 3 9
2 6 8
6 1 7
```
#### 输出 #1
```
22
```
### 说明/提示
#### 数据规模与约定
对于 $100\%$ 的数据,保证 $1≤n≤10000$ , $1≤a_i,b_i≤n$ , $-1e5≤c_i≤1e5$ 。
### Code (权值有负)
此处蒟蒻一开始并没有用树形dp去做,思想是对于树上的**任意结点**,都对其找**最远** $d1$ 和**次远** $d2$ 的结点,一边遍历,一边**打擂台比大小**,找**最长的路径长度**。
为什么此处不能直接二次 $dfs$ 呢,是由于我们的 $dfs$ 是对树的**各个结点的深度**进行储存,如果有**负边权**,就会**影响** $dist[]$ 的答案,使得最后的答案会不正确(蒟蒻的个人想法,欢迎各位大佬斧正~~) 。
```cpp
#include<bits/stdc++.h>
using namespace std;
const int N=1e6;
int n,a,b,c,ans;
struct Edge {
int v,nxt;
int w;
}edge[N<<1];
int head[N],idx;
void add(int x,int y,int z) {
edge[++idx].v=y;
edge[idx].nxt=head[x];
edge[idx].w=z;
head[x]=idx;
}
int dfs(int u,int fa) {
int d1=0,d2=0,dist=0;
for(int i=head[u];i;i=edge[i].nxt) {
int v=edge[i].v;
int w=edge[i].w;
if(v==fa) continue;
int d=dfs(v,u)+w;
dist=max(d,dist);
if(d>d1) {
d2=d1;
d1=d;
} else if(d>d2) d2=d;
}
ans=max(d1+d2,ans);
return dist;
}
int main() {
scanf("%d",&n);
for(int i=1;i<n;i++) {
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
add(b,a,c);
}
dfs(1,0);
printf("%d\n",ans);
return 0;
}
```
~~但为了凸显我们信息学的举一反三的优良学习精神,我们就大方的开个数组。~~
~~其实也没什么用,反正空间爆不了。~~
下面是改进的代码 ~~(啥也不是)~~ :
```cpp
#include<bits/stdc++.h>
using namespace std;
const int N=1e6;
int n,h[N],a,b,c,ans;
struct Edge {
int v,nxt;
int w;
}edge[N<<1];
int head[N],idx;
int f[N];
void add(int x,int y,int z) {
edge[++idx].v=y;
edge[idx].nxt=head[x];
edge[idx].w=z;
head[x]=idx;
}
int dfs(int u,int fa) {
int d1=0,d2=0;
for(int i=head[u];i;i=edge[i].nxt) {
int v=edge[i].v;
int w=edge[i].w;
if(v==fa) continue;
int d=dfs(v,u)+w;
f[u]=max(d,f[u]);
if(d>d1) {
d2=d1;
d1=d;
} else {
if(d>d2)
d2=d;
}
}
ans=max(d1+d2,ans);
return f[u];
}
int main() {
scanf("%d",&n);
for(int i=1;i<n;i++) {
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
add(b,a,c);
}
dfs(1,0);
printf("%d\n",ans);
return 0;
}
```
## 拓展
**树的中心**为“到所有点的最大距离“**最小的节点**。而定义树的“**几何中心**”,除了在节点上,还可以处于某条边中。
那么有**性质**:
当**边权为正**时,**所有直径都经过(几何)中心**。
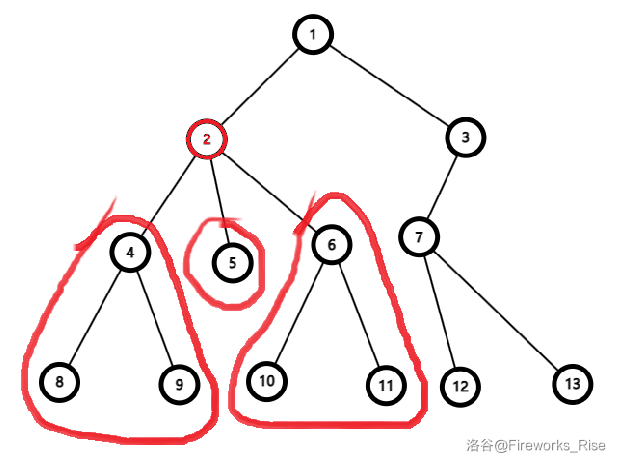
**证明:**
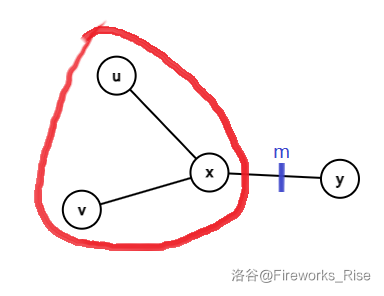
显然,**几何中心**可以把树分为**多棵子树**,而一条直径经过几何中心**当且仅当这条直径的两端点在不同子树中**。容易看出,若**一条直径的两端在同一子树中**,那么将此时的“伪几何中心”向这课子树方向移动显然**只会让这个最大距离进一步变小**。
如图,显然有 $(m,y)<(x,y)\le \min((u, x), (v,x))< \min((m,u),(m,v))$ 。
显然,若**所有直径经过几何中心**,则所有直径**要么都经过某条边及其两端点**(其中至少一个为中心),要么**经过中心**,证毕。
---
## 树形dp 之 树形背包类
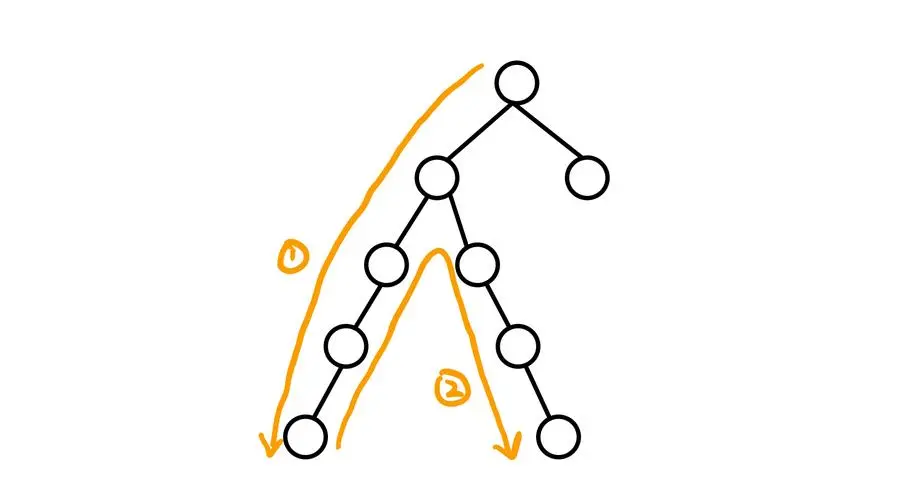
~~请让蒟蒻说说~~**树形背包类**的一般转移方程:
$\begin{cases}
f_{v,k}=f_{u,k}+a_v\\
f_{u,k}=\max(f_{u,k},f_{v,k-1})
\end{cases}.
树形背包,就是背包加上条件,在树上进行背包选择,一个物品只有选择了它的主件(父亲结点) 才能选择。
题目来源 洛谷P2015 苹果树
题目描述
有一棵苹果树,如果树枝有分叉,一定是分二叉(就是说没有只有一个儿子的结点)
这棵树共有 N 个结点(叶子点或者树枝分叉点),编号为 1∼N,树根编号一定是 1。
我们用一根树枝两端连接的结点的编号来描述一根树枝的位置。下面是一颗有 4 个树枝的树:
2 5
\ /
3 4
\ /
1
现在这颗树枝条太多了,需要剪枝。但是一些树枝上长有苹果。
给定需要保留的树枝数量,求出最多能留住多少苹果。
输入格式
第一行 2 个整数 N 和 Q ,分别表示表示树的结点数,和要保留的树枝数量。
接下来 N−1 行,每行 3 个整数,描述一根树枝的信息:前 2 个数是它连接的结点的编号,第 3 个数是这根树枝上苹果的数量。
输出格式
一个数,最多能留住的苹果的数量。
说明/提示
### 解题思路
经分析,本题需要在树上进行动态规划,故使用树形dp。
#### I.建立树
任何相邻的两个节点**没有优先级关系**,所以用**邻接表**储存树,如果把这棵树看做一个**图**,即是**无向无环连通图**,此处不用多讲,比较简单实现。
#### II.dp 随着 dfs 动规整棵树
此题已明确给出了根节点为 $1$,我们就无需多开一个 $degree$ 数组来找**入度为** $0$ **的结点**了,**直接进行遍历**。
**状态转移**方程:
$f_{i,j}$ 表示以 $i$ 为结点的子树,保留 $j$ 个树枝,最多能留住的苹果数量
$f_{u,j}=\max(f_{u,j},f_{u,j-k-1}+f_{v,k}+w)
当前状态可从以子节点 v 为根的子树保留 k 个树枝的苹果数量 f_{v,k},加上本身结点 u 剩下 j-k-1 个树枝保留的苹果数量,这里多减的一个 1 是因为要保留 u,v 之间相连的连边,也即 f_{u,j-k-1} 转移过来。
注意:i,j需要倒序枚举,因我们此处进行的是01背包。
Code
#include<bits/stdc++.h>
using namespace std;
const int N=1001;
int n,q,a,b,c;
struct Edge {
int v,w,nxt;
}edge[N<<1];
int head[N],idx;
int f[N][N];
void add(int x,int y,int z) {
edge[++idx].v=y;
edge[idx].nxt=head[x];
edge[idx].w=z;
head[x]=idx;
}
void dfs(int u,int fa) {
for(int i=head[u];i;i=edge[i].nxt) {
int v=edge[i].v;
int w=edge[i].w;
if(v==fa) continue;
dfs(v,u);
for(int j=q;j>=0;j--) {
for(int k=0;k<j;k++)
f[u][j]=max(f[u][j],f[u][j-k-1]+f[v][k]+w);
}
}
}
int main() {
scanf("%d%d",&n,&q);
for(int i=1;i<n;i++) {
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
add(b,a,c);
}
dfs(1,0);
printf("%d\n",f[1][q]);
return 0;
}
树形dp的 n^2 优化
本题如果需要优化时间的话,需要在进行动态规划的循环进行上下界限优化,
( 1 \le i \le \min(q,sz_u) , 0 \le j \le \min(sz_v,i-1) )
我在做题一开始没意识到可以优化,所以code程序没有进行优化,大家可以自行修改。
再拿 洛谷P2014 选课 这道经典的树形dp例题来讲,抛开题目,如果学某个课程前不只需要学其他的一个课程,而是一些课程(课程数目≥ 2,即每个结点的入度最多为 1 ),这样更好理解优化。
首先上两个都可以过本题的代码,以方便作比较。
Code
#include<bits/stdc++.h>
using namespace std;
const int N=301;
int n,m,a,b[N];
struct Edge {
int v,nxt;
}edge[N<<1];
int head[N],idx;
int f[N][N];
void add(int x,int y) {
edge[++idx].v=y;
edge[idx].nxt=head[x];
head[x]=idx;
}
void dfs(int u) {
f[u][1]=b[u];
for(int i=head[u];i;i=edge[i].nxt) {
int v=edge[i].v;
dfs(v);
for(int j=m+1;j>=0;j--) {
for(int k=0;k<j;k++)
f[u][j]=max(f[u][j],f[u][j-k]+f[v][k]);
}
}
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) {
scanf("%d%d",&a,&b[i]);
add(a,i);
}
dfs(0);
printf("%d\n",f[0][m+1]);
return 0;
}
Code 2 (优化)
#include<bits/stdc++.h>
using namespace std;
const int N=301;
int n,m,a,b[N];
struct Edge {
int v,nxt;
}edge[N<<1];
int head[N],idx;
int f[N][N],sz[N];
void add(int x,int y) {
edge[++idx].v=y;
edge[idx].nxt=head[x];
head[x]=idx;
}
void dfs(int u) {
f[u][1]=b[u];
sz[u]=1;
for(int i=head[u];i;i=edge[i].nxt) {
int v=edge[i].v;
dfs(v);
for(int j=min(m+1,sz[u]+sz[v]);j>=0;j--) {
for(int k=0;k<=min(sz[v],j-1);k++)
f[u][j]=max(f[u][j],f[u][j-k]+f[v][k]);
}
sz[u]+=sz[v];
}
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) {
scanf("%d%d",&a,&b[i]);
add(a,i);
}
dfs(0);
printf("%d\n",f[0][m+1]);
return 0;
}
小总结
通过对比观察两次的数据,可以发现两个代码在用时上有差距,而且这是在 1 \le N \le 300 这么小的数据下比较,如果 n=1000 甚至 10000 的时候呢。
从程序上来看最主要的差别在于进行dp操作的两个循环的范围 :
程序 1 的 main part
for(int j=m+1;j>=0;j--) {
for(int k=0;k<j;k++)
f[u][j]=max(f[u][j],f[u][j-k]+f[v][k]);
}
程序 2 的 main part
for(int j=min(m+1,sum[u]+sum[v]);j>=0;j--) {
for(int k=0;k<=min(sum[v],j-1);k++)
f[u][j]=max(f[u][j],f[u][j-k]+f[v][k]);
}
这乍一看,好像没啥差别。
可是你不能小看了这步操作,他可起了很大的作用,光表面说是没用的。
但如果用大佬的一大堆数学结论方法证明,我们这些小蒟蒻是看不懂的 。
那就用最通俗易懂 的方法来解释吧。
我们把这两个循环做的事看作是两组数进行乘法原理的匹配,
此处的 $sum_v$ 是以当前访问结点为根的**子树的大小**(包括当前根结点),其实是个非常小的常数,这里做解释时为了方便,暂时省略,但在优化程序时**不能省略**(可能会导致 WA 出错),因为自己也**可以从本身所处的子树集里的节点转移状态过来**。
而**每次匹配**操作都会出现和以前**不一样的数对**。
当访问完所有结点后,所得出来的**全部数对都不重复**。
这样**时间复杂度**就可以转换为了一个**组合问题**:
$C_{2}^{n}=\frac{n*(n-1)}{2}
再加上原来省略的常数,就接近 O(n^2) 的时间复杂度了。
大佬的严格证明,感兴趣的数学大佬可以尝试去理解,本蒟蒻就不参与了。
这里的优化省略了常数,其实当 n 很大时,这个常数也比较大,经过我和我校的几位大佬的一番讨论,虽然接受全网大佬们严格的证明,优化后肯定是平方级别的时间复杂度,但是经过试验,如果样例故意卡,那么这个省略的常数还是不可估量的大 (虽然还是比 n^3 快上不少) 。
所以在做树形dp的题型时,我们尽量做到能优化就优化,尽量想办法把时间复杂度从 O(n^3) 压缩到 O(n^2) 平方级。
总结
给定一棵有N个节点的树(通常是无根树,也就是有 N-1 条无向边),我们可以任选一个节点为根节点,从而定义出每个节点的深度和每棵子树的根。
在树上设计动态规划算法时,一般就以节点从深到浅(子树从小到大)的顺序作为dp的“阶段”。在状态表示中,第一维通常是节点编号(代表以该节点为根的子树)。
大多数时候,我们采用递归的方式实现树形动态规划。对于每个节点 u ,先递归在它的每个子节点上进行动态规划dp,在回溯时,从子节点向节点 u 进行状态转移。
最主要的题型主要用于:
①.选择节点类
②.树形背包类
③.树的直径类
题库
可以先浅浅练练基础 ,建议可以参考一下我的学习题单 洛谷【树形dp】 ID:970993