P8799 题解
BBD_XBC
·
·
题解
这个题解主要是写给那些还没学过角速度的同学
一:齿轮比
先引入一个概念:齿轮比
G = \dfrac{C}{F}
我们可以这样理解:若齿轮比为 $\dfrac{36}{12}$,化简得 $\dfrac{3}{1}$,**说明输入齿轮转三圈,输出齿轮转一圈**。
在这到题目中,**由于齿轮数与周长成正比关系,而周长又与半径成正比关系**。所以:
$G = \dfrac{C_2}{C_1} = \dfrac{r_2}{r_1}
二:角速度
如果我们已经计算出齿轮比,且知道输入速度,则有:
\omega_2 = \dfrac{\omega_1}{G}
角速度是什么?
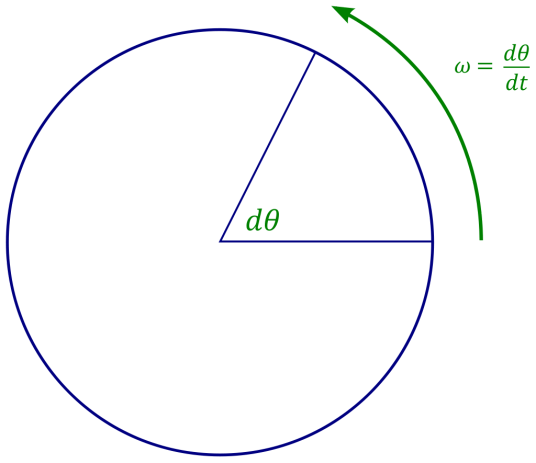
简单来讲,角速度描述了物体绕圆心运动的**快慢**。
### 三:推导
了解了前置知识,我们来看推导:
设第一个齿轮角速度为 $\omega_1$,半径为 $r_1$,第二个齿轮半径为 $r_2$,角速度为:
$\omega_2 = \dfrac{\omega_1}{G} = \dfrac{\omega_1}{\frac{r_2}{r_1}} = \omega_1 \times \dfrac{r_1}{r_2}
那对于一串连续的齿轮,设有 n 个,则有:
\omega_n = \omega_1 \times \dfrac{r_1}{r_2} \times \dfrac{r_2}{r_3} \times \dfrac{r_3}{r_4} \times \cdots \times \dfrac{r_{n-1}}{r_n} = \omega_1 \times \dfrac{r_1}{r_n}
那对于题目中要求的 q,就可以表示了:
q = \dfrac{\omega_n}{\omega_1} = \dfrac{r_1}{r_n}
换句话说,半径与角速度成反比。
由此得出:题目要求的是在所有半径中是否有一对数比值为 q。
四:做法
- 最朴素的做法:对于每次询问,用 O(n^2) 的时间复杂度求出每对比值。至于效果嘛,自己清楚。。。
- 稍微想了一下的做法:题目已经给出 q 了,那所以开桶排,对于每一个半径 r_i 都去判断 r_i \times q 的位置上有没有另一个 r。但我亲身试过,不可以。
-
五:代码
这么多大佬都发了代码,我就不贴这里了,想看的去搜记录。