题解 P5410 【【模板】扩展 KMP(Z 函数)】
泥土笨笨
·
·
题解
前置知识
KMP算法 可以参考小花的博客:字符串学习笔记 · 浅析KMP——单模式串匹配算法 模板题:P3375 【模板】KMP字符串匹配
做完模板题有兴趣的话也可以做做下面的题目,会加深对KMP算法的理解:
P2375 [NOI2014] 动物园
P4391 [BOI2009]Radio Transmission 无线传输
扩展KMP算法
问题定义
给出两个字符串,其中一个是文本串s,一个是模板串p。求s的每一个后缀与p的最长公共前缀的长度。
这个问题看起来很绕。不妨设s串的长度为sl,p串长度为pl,我们定义字符串都是从下标0开始,用s[i,j]表示s串从i下标开始,到j下标位置结束的子串。那么扩展KMP算法这个问题,也可以表述成:
分别求s[0,sl-1],s[1,sl-1],s[2,sl-1],...,s[sl-1,sl-1]与p串最长公共前缀的长度。即最开始是用s与p匹配,然后去掉s的第一个字符,再匹配,再去掉开头第一个字符,再匹配……
我们不妨把每个答案都存在ext数组里面,即:
$s[1,sl-1]$与$p$的最长公共前缀的长度存在$ext[1]$里面,
$s[2,sl-1]$与$p$的最长公共前缀的长度存在$ext[2]$里面,
......
$s[sl-1,sl-1]$与$p$的最长公共前缀的长度存在$ext[sl-1]$里面,
我们要求的就是整个$ext$数组的值。
## 例子
模板题中,文本串$s$是`aaaabaa`,模板串$p$是`aaaaa`,那么先把两个字符串开头的地方对齐,
```
aaaabaa
aaaaa
```
可以看出,$s[0,6]$与$p$的最长公共前缀是`aaaa`,所以$ext[0]=4$,
然后把模板串向右移动一位,再跟文本串s匹配:
```
aaaabaa
aaaaa
```
可得,$s[1,6]$与$p$的最长公共前缀是`aaa`,所以$ext[1]=3$,
以此类推,每次移动模板串一位,进行匹配即可,可以算出所有的答案。但是这种方式效率太低了。
## 优化的思路
在刚刚求$ext[1]$的过程中,其实我们知道$p$开头有`aaa`,而$s$从$1$位置开始也是有`aaa`,其实我们只需看$s[4]$位置的`b`和$p[3]$位置的`a`是否匹配就可以决定$ext[1]$了,这个信息如果能被我们提前获知并利用,就可以节约很多时间。
假设现在有图灵的帮助,我们得到了一个神奇的数组$z$,这个数组的定义是:
$z[i]$表示模板串的子串$p[i,pl-1]$与$p$的最长公共前缀的长度。我们发现这个数组不是用文本串$s$和模板串$p$进行匹配,而是用模板串自己匹配自己得到的。我们姑且先不管这个数组是怎么求出来的,假设已知这个数组每个位置的值,那么我们能否优化前面的计算呢?
我们已经求出了$ext[0]$,现在要求$ext[1]$了。因为$ext[0]=4$这个信息已知,那么相当于我们知道了$s[0,3]=p[0,3]$,当然就有$s[1,3]=p[1,3]$,即两个字符串从$1$号位置开始,连续$3$个都是一样的。即下图中的两条红色线相等。
图灵告诉我们,$z[1]=4$,这个如果你不信,可以手算看看。那么我们就知道了,$p[0,3]=p[1,4]$,也就是下图中绿色两条线相等。
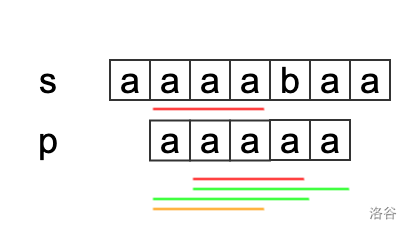
这时候,我们可以发现什么?第二条红线和第一条绿线是重合了$3$个位置的,把第一条绿线向左平移一个位置,就可以发现,红色的线和橙色的线是相等的!
所以,当我们求$ext[1]$的时候,我们不需要看橙色线代表的$3$个`a`了,因为他们一定相等,我们直接比较$s[4]$位置的`b`和$p[3]$位置的`a`是否匹配,就可以决定$ext[1]$了,这就是扩展KMP算法节约时间的原理。
## 一般的情况
先看一张图片
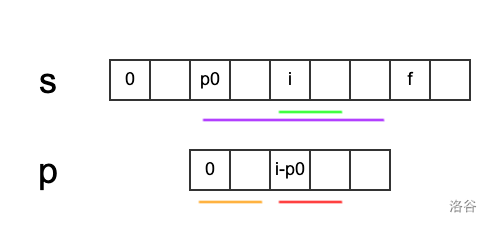
还是刚才的问题,假设我们目前循环到$s$串的$i$位置,在$i$前面的$ext$数组的值我们都知道了。所以目前在求$s[i,sl-1]$这个串和$p$的最长公共前缀的长度,就是要考虑以$i$开头的情况了。
假设之前匹配过程中,在$s$中走到最远的位置不会超过$f$,即对于$j<i$,$j+ext[j]$最大的时候的取值是$f$,这时候的$j$我们记做$p0$,把模板串$p$移动到跟$p0$对齐的位置。那么就画出上面的图了。此时$f=p0 + ext[p0]
这个时候i位置对应在p串里面的下标是i-p0,那么红色的线表示的是z[i-p0],它跟橙色的线长度相等。这个时候取跟红色对应的绿色一段,它的右端点是i + z[i - p0]
情况1
如果i + z[i - p0] < p0 + ext[p0],即绿线不超过紫色的线。那么因为紫色的线是上下对齐的,我们可以知道绿色的线等于红色的线,而红色的线又等于黄色的线,所以绿色长度等于黄色长度。
那么此时ext[i]就直接等于绿色的长度了。它就是从i开头,和p匹配的最长的前缀的长度。ext[i]不可能比绿线更长了,因为如果是这样,那么红色线也会延长,而红色和黄色必然相等,因为这个是z[i-p0]的定义。那么黄色线也要延长,这样ext[i]又增加了。所以ext[i]总是等于z[i - p0]
代码里面是这样的:
if (i + z[i - p0] < p0 + ext[p0]) {
ext[i] = z[i - p0];
}
情况2
如图:
不好处理的情况是,和红线对应的绿线,超过了紫线的范围。紫线范围内,根据上下对应,我们总能保证是一样的,但是超过紫线的部分,我们就无能为力了,所以此时我们只能从f位置开始,尝试匹配。
也就是说,我们只能保证,绿线开头的一部分,跟下面对应的橙色线一样。根据z数组的定义我们可以把橙色线移动到p开头去,那么橙色长度的部分都不用再匹配了,我们只需从s的f位置开始,去看和p的now位置是否匹配。
那么这个now如何计算呢?i到f的长度和0到now的长度是相等的,那么i到f的长度可以计算出来是p0+ext[p0]-i,那么p字符串又是从0开始,那么now=p0+ext[p0]-i,从这个位置开始暴力匹配:
代码:
now = p0 + ext[p0] - i;
now = max(now, 0);//防止i太大
while (now < pl && now + i < sl && p[now] == s[now + i]) {now++;}
ext[i] = now;
p0 = i;
求z数组
现在我们已经会匹配了,那么z数组怎么来呢?难道真的找图灵要?回头看一下z数组的定义:
而我们要求的ext数组是:
$ext[i]$表示文本串的子串$s[i,pl-1]$与$p$的最长公共前缀的长度。
所以,求$ext$和求$z$的过程是一样的。只需把自己当成文本串,用自己匹配自己。是不是有KMP算法求$next$数组那个味儿了?
## 复杂度
复杂度和KMP一样,是$O(sl+pl)$的。
最后是代码时间:
```cpp
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int MAXN = 2e7 + 5;
char p[MAXN], s[MAXN];
int pl, sl, z[MAXN], ext[MAXN];
void getZ() {
z[0] = pl;//从0号位置开始,LCP就是全部字符串
//从1开始,先暴力算
int now = 0;
while (now + 1 < pl && p[now] == p[now + 1]) now++;
z[1] = now;
int p0 = 1;
for (int i = 2; i < pl; ++i) {
if (i + z[i - p0] < p0 + z[p0]) {
z[i] = z[i - p0];//第一种情况
} else {
now = p0 + z[p0] - i;
now = max(now, 0);
while (now + i < pl && p[now] == p[now + i]) now++;
z[i] = now;
p0 = i;
}
}
}
void exkmp() {
getZ();
//先暴力算ext[0]
int now = 0;
while (now < pl && now < sl && p[now] == s[now]) now++;
ext[0] = now;
int p0 = 0;
for (int i = 1; i < sl; ++i) {
if (i + z[i - p0] < p0 + ext[p0]) {
ext[i] = z[i - p0];
} else {
now = p0 + ext[p0] - i;
now = max(now, 0);//防止i太大
while (now < pl && now + i < sl && p[now] == s[now + i]) now++;
ext[i] = now;
p0 = i;
}
}
}
int main() {
scanf("%s%s", s, p);
pl = strlen(p);
sl = strlen(s);
exkmp();
long long a0 = 0, a1 = 0;
for (int i = 0; i < pl; ++i) {
a0 ^= 1LL * (i + 1) * (z[i] + 1);
}
for (int i = 0; i < sl; ++i) {
a1 ^= 1LL * (i + 1) * (ext[i] + 1);
}
printf("%lld\n%lld\n", a0, a1);
return 0;
}
```