矩阵优化
Imakf
·
·
个人记录
\Huge\text{矩阵优化}\ \mathcal{DP}
作者:Imakf
概述
在信息学竞赛中,我们常常会遇到一类 \mathcal{DP} 、递推问题,如快速求线性齐次常系数递推方程的某一项,直接模拟会 \rm TLE、快速求有向图从 u 到 v 有多少条不同路径等等。有另一类 \mathcal{DP} 要求支持单点修改某些参数多次查询。它们都可以使用矩阵乘法进行优化,这些“转移矩阵”一般都是较小的。下面我将会着重分析一些例题,讲解此类题目的一些做法。希望读者能在看完本篇后,对矩阵优化 \mathcal{DP} 有更直观的印象。
本论文不会对某些性质进行证明,有能力的读者请自行搜索相关资料。
前置知识:矩阵乘法。
线性递推
例题 1.1 洛谷P1962 斐波那契数列
F_i=
\begin{cases}
1 & i =1,2\\
F_{i-1}+F_{i-2} & i \ge3
\end{cases}
给定 k\ (1 \le k\le 10^{18}),求 F_k。答案取模。
分析
本题算是矩阵优化递推的入门级别题目。
设当前 \mathcal{DP} 数组为 \begin{bmatrix} F_{i-1} \\ F_{i-2}\end{bmatrix}。
尝试构造一个矩阵,使得每次左乘以后都能得到下一个“阶段”的新 \mathcal{DP} 数组。即:
B
\times
\begin{bmatrix}
F_{i-1} \\
F_{i-2}
\end{bmatrix}
=
\begin{bmatrix}
F_{i} \\
F_{i-1}
\end{bmatrix}
一般来说,我们把 B 称作转移矩阵。
经过一番精心构造,可以得到:
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
\times
\begin{bmatrix}
F_{i-1} \\
F_{i-2}
\end{bmatrix}
=
\begin{bmatrix}
F_{i} \\
F_{i-1}
\end{bmatrix}
是符合递推式的定义的。
矩阵乘法是具有结合律的,所以我们可以先计算 B^k,再与 \mathcal{DP} 数组相乘。关于一些实现上的问题,请在做题中寻找经验教训。
时间复杂度 O(2^3\log k)。
例题 1.2
F_i=
\begin{cases}
1 & i =1,2\\
F_{i-1}+F_{i-2} & i \ge3
\end{cases}
给定 k\ (1 \le k\le 10^{10^5}),求 F_k。答案取模。
分析
发现 $k$ 难以读入,我们用一个数组 $S$ 从高到低把它的每一位存下。
然后求出转移矩阵 $B$ 的 $B^{10},B^{1000},\cdots,B^{10^x}$,再选出需要的转移矩阵相乘,把指数凑出即可。
当然你不一定要选择 $10$ 进制,$10$ 进制只是方便读入,在复杂度方面并没有优势。
时间复杂度 $O(2^3\log 10\log k)$。
### 例题 $1.3$ CF1117D Magic Gems
你有很多魔法宝石。每颗魔法宝石可以分解成 $m$ 颗普通宝石,魔法宝石和普通宝石都占据 $1$ 体积的空间,但普通宝石不能再被分解。让一些魔法宝石分解,使得所有宝石占据的空间**恰好**为 $n$ 单位体积。求可以让最后得到的宝石**恰好**占据 $n$ 单位体积的分解方案。两种分解方案不同当且仅当分解的魔法宝石数量不同,或者是进行分解的宝石的位置不同。答案取模。
$1 \le n \le 10^{18},2\le m \le 100$。
#### 分析
容易发现递推式为:
$$
F_i=
\begin{cases}
1 & i \le 0\\
F_{i-1}+F_{i-m} & i \ge1
\end{cases}
$$
其中 $F_{i-1}$ 表示选择不分解,$F_{i-m}$ 表示分解。
容易发现我们的 $\mathcal{DP}$ 状态必须保存 $F_{i-1},F_{i-2},\cdots,F_{i-m}$。尝试构造一个矩阵转移:
$$
\begin{bmatrix}
1 & 0 & \cdots & 1 \\
1 & 0 & \ddots & 0 \\
0 & 1 & \ddots & 0\\
\vdots & \ddots & \ddots & \vdots
\end{bmatrix}
\times
\begin{bmatrix}
F_{i-1} \\
F_{i-2}\\
\vdots\\
F_{i-m}
\end{bmatrix}
=
\begin{bmatrix}
F_{i}\\
F_{i-1}\\
\vdots\\
F_{i-m+1}
\end{bmatrix}
$$
时间复杂度 $O(m^3 \log n)$。
### 例题 $1.4$ BZOJ3329 Xorequ
给定正整数 $n$,现有方程:$x \operatorname{xor} 3x=2x
-
求出有多少个 \le n 的正整数解;
-
求出有多少个小于 \le 2^n 的正整数解,模 10^9+7。
分析
这题是数位 \mathcal{DP} 与矩阵优化 \mathcal{DP} 的一个结合。
在不进位的情况下有 $x+2x=3x$,肯定有 $x \operatorname{xor} 2x=3x$,这是充分条件。
于是题目条件就是 $x$ 不能有两位相邻的 $1$。
第一问直接数位 $\mathcal{DP}$ 解决。
第二问用矩阵优化解决。
## 路径问题
### 例题 $2.1$ 洛谷 P3758 [TJOI2017]可乐
加里敦星球有 $n$ 个城市,$m$ 条有向边。可乐机器人放在了加里敦星球的 $1$ 号城市上。这个可乐机器人有三种行为: 停在原地,去下一个相邻的城市,自爆。它每一秒都会随机触发一种行为。现在给加里敦星球城市图,在第 $0$ 秒时可乐机器人在 $1$ 号城市,问经过了 $t$ 秒,可乐机器人的行为方案数是多少?答案模 $2017$。
$1 \le n \le 30,1 < t \le 10^6,0< m \le 100$。
#### 分析
设邻接矩阵为 $A$,$A_{i,j}$ 表示 $i \rightarrow j$ 的路径条数。容易发现,经过一轮以后,$A_{i,j}$ 变成了 $\sum\limits_{k=1}^{n}A_{i,k}\cdot A_{k,j}$。这就是矩阵乘法的定义式。本题还有一个自爆行为,可以加入一个__自爆节点__ $0$,让每个城市都与他连边,并让自爆节点有一个自环即可。
最后只需查询 $\sum\limits_{i=0}^{n} A_{1,i}$。
时间复杂度 $O(n^3\log t)$。
### 例题 $2.2$ [NOI Online #3 提高组]魔法值
H 国的交通由 $n$ 座城市与 $m$ 条道路构成,无重边自环。
H 国是一个信奉魔法的国家,在第 $j$ 天,$i$ 号城市的魔法值为 $f_{i,j}$。H 国的魔法师已观测到第 $0$ 天时所有城市的魔法值 $f_{i,0}$,且他们还发现,之后的每一天每个城市的魔法值,都将会变为所有与该城市直接相连的城市的前一天魔法值的异或值。
现在 H 国的国王问了你 $q$ 个问题,对于第 $i\ (1\le i \le q)$个问题你需要回答:第 $a_i $ 天时 $1$ 号节点的魔法值是多少。
$1 \le n,q \le 100,1 \le m \le \frac{n(n-1)}{2},1 \le a_i < 2^{32},0 \le f_{i,0} < 2^{32}$。
#### 分析
##### 算法 $1
容易发现,我们只需要知道所有点到 1 的路径数量 \bmod 2 后的值。
容易发现,只要对上题改变模数即可,或者直接把运算改成异或。
容易发现时间复杂度 O(qn^3\log a),过不去。
因为只需要知道 \bmod 2 后的值,直接 \rm{bitset} 优化异或的过程就可以了。
不开 O2 会常数过大,考虑使用 unsigned long long 压位也是可以的。
时间复杂度 O(\dfrac{qn^3\log a}{64})。
算法 2
预处理出转移矩阵的 B^{2^0},B^{2^1},\cdots,B^{2^{31}}。
然后通过二进制找到需要的转移矩阵(最多 31 个),暴力一个一个与 \mathcal{DP} 数组相乘,因为 \mathcal{DP} 数组仅为一个向量(n\times1 的矩阵),所以乘法的复杂度是 O(n^2) 而不是 O(n^3)。
复杂度 O(qn^2 \log a)。
例题 2.3 [NOI Online #1 入门组]魔法
C 国由 n 座城市与 m 条有向道路组成,城市与道路都从 1 开始编号,经过 i 号道路需要 t_i 的费用。
现在你要从 1 号城市出发去 n 号城市,你可以施展最多 k 次魔法,使得通过下一条道路时,需要的费用变为原来的相反数,即费用从 t_i 变为 -t_i。请你算一算,你至少要花费多少费用才能完成这次旅程。
#### 分析
本题十分有意思,为出题人点赞!
首先我们求出 $F[1]_{i,j}$ 表示 $i \rightarrow j$ 使用一次魔法的最少花费。
这个可以 `Floyd`,直接分层图。
我们考虑从使用一次魔法推到使用两次魔法:$F[2]_{i,j}=\min\limits_{k=1}^{n}F[1]_{i,k}+F[1]_{k,j}$。
从两次魔法推到三次 $F[3]_{i,j}= \min\limits_{k=1}^{n} F[2]_{i,k}+F[1]_{k,j}$。
结论是,你依然可以用矩阵乘法维护这个转移。只要把原来矩阵乘法中的 $+$ 换成 $\min$,$\times$ 换成 $+$ 即可。我们一般叫它__广义矩阵乘法__。
复杂度 $O(n^3\log k)$。
## 动态 $\mathcal{DP}
例题 3.1 SP1716 GSS3 - Can you answer these queries III
给定长度为 n 的序列 A,执行 q 次操作,操作共两种:
- 把 A_x 修改成 y;
- 求 [l,r] 的最大子段和,不能为空。
#### 分析
我们回顾暴力如何做此题:把区间提出,然后计算以每个位置为结尾的最大子段和。$f_i=\min(f_{i-1}+A_i,A_i)$,然后取所有 $f_i$ 的最大值即可,不妨设 $g_i=\max\limits_{j=1}^{i}f_j$。
考虑我们当前有一个 $\mathcal{DP}$ 数组:$\begin{bmatrix} f_{i-1} \\ g_{i-1}\end{bmatrix}$,我们需要让它的下标转移到 $i$。
发现这绝对是一般的矩阵乘法做不到的,不如仿照【例题 $2.3$】,我们修改矩阵乘法的运算方式。将取 $\min$ 改成取 $\max$ 依然可行。
于是就可以得到:
$$
\begin{bmatrix}
A_i & -\infty \\
A_i & 0
\end{bmatrix}
\times
\begin{bmatrix}
f_{i-1}\\
g_{i-1}
\end{bmatrix}
=
\begin{bmatrix}
f_{i}\\
g_{i}
\end{bmatrix}
$$
这样子会漏掉一种情况,即单独只选取 $A_i$ 的情况,所以我们被迫把转移矩阵修改为 $3\times 3$。
$$
\begin{bmatrix}
A_i & A_i &-\infty \\
-\infty & 0 & -\infty \\
A_i & A_i & 0
\end{bmatrix}
\times
\begin{bmatrix}
f_{i-1}\\
0 \\
g_{i-1}
\end{bmatrix}
=
\begin{bmatrix}
f_{i}\\
0\\
g_{i}
\end{bmatrix}
$$
我们只需要用__线段树维护矩阵乘积__就可以在 $O(3^3\log n)$ 复杂度内完成查询,修改直接修改矩阵的值 $O(3^3\log n)$ 完成修改。
时间复杂度 $O(3^3q \log n)$。
### 例题 $3.2$ NOIp2018 提高组 保卫王国
给定一棵树,每个点有点权,$m$ 组询问,每次指定两个点能选或不能选,求最小权覆盖集。
$10 \le n ,m\le 10^5$,答案在 `long long` 以内。
#### 分析
最小权覆盖集 = 全集 - 最大权独立集。暴力做是 $O(nm)$ 的,不赘述。
每次指定选或不选,可以视作改变权值,加上或减去无穷大。
这样子可以视作动态修改权值,每次询问 $\mathcal{DP}$ 答案。
序列问题我们采用线段树,树上问题我们可以考虑__树链剖分__。
树链剖分后,仿照上两道题我们用矩阵乘法可以容易维护一条重链上的答案,但是我们要求的是有关于子树的 $\mathcal{DP}$,轻链也要被计算,那该怎么办呢?
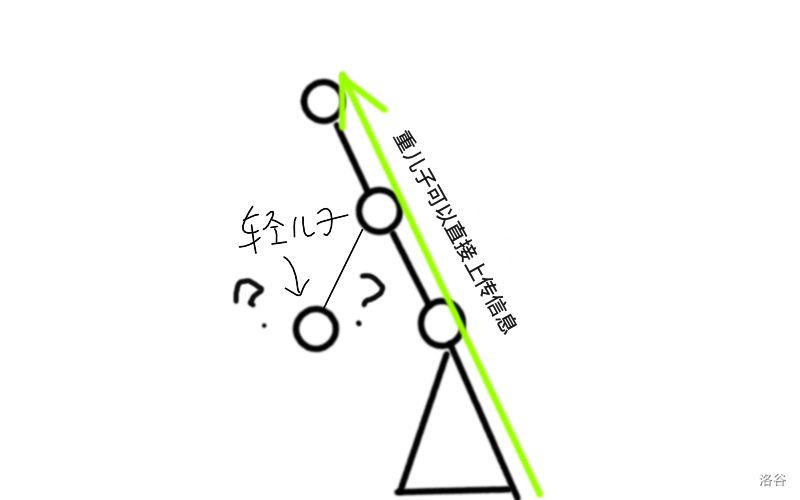
具体来说我们要维护一个这样的东西($hs$ 代表重儿子):
$$
\begin{bmatrix}
? & ? \\
? & ?
\end{bmatrix}
\times
\begin{bmatrix}
dp_{hs,0} \\
dp_{hs,1}
\end{bmatrix}
=
\begin{bmatrix}
dp_{x,0} \\
dp_{x,1}
\end{bmatrix}
$$
我们知道, $\mathcal{DP}$ 数组存有有两个信息:选了它子树最优、不选它子树最优。
在我们之前的问题中,要进行修改的都是一些参数。在这里,修改的是点权,我们也很容易联想到把点权丢到转移矩阵中来转移。很遗憾,单纯这么做是不行的。
考虑把所有的轻儿子的贡献丢到__转移矩阵中__。这个值也可以被看成是个动态的参数。
令 $dp_{i,0/1}$ 表示该节点 $i$ 选/不选,的最大权独立集是多少。
假设 $x$ 为当前节点,$lc$ 为某一个轻儿子。当前还未计算 $lc$ 对 $x$ 的影响。那我们应该让:
- $dp_{x,1}+=dp_{lc,0}
-
dp_{x,0}+=\max(dp_{lc,0},dp_{lc,1})
完全可以用简单的加减完成这项操作。修改一个点权,我们只需要算出以 lc 为根的子树答案。把原先加上去的值减掉,再修改点权,重新算一遍子树答案,再把这个值加上去即可。
所以我们记录两个辅助参数:
w_0=\sum\limits_{lc \text{ is son of } x} \max(dp_{lc,0} ,dp_{lc,1}),w_1=A_x+\sum\limits_{lc \text{ is son of } x} dp_{lc,0}
分别表示 x 在不选/选的情况下轻儿子和 x 本身能造成的最大贡献(即不算重儿子的贡献)。
转移直接:
\begin{bmatrix}
w_0 & w_0 \\
w_1 & -\infty
\end{bmatrix}
\times
\begin{bmatrix}
dp_{hs,0} \\
dp_{hs,1}
\end{bmatrix}
=
\begin{bmatrix}
dp_{x,0} \\
dp_{x,1}
\end{bmatrix}
修改的时候,我们首先单独修改被修改点的矩阵,把 w_1 中的 A_x 更换。修改了这个点矩阵的时候,我们在对应的重链的线段树上进行修改,此时会改变重链顶部的 \mathcal{DP} 值,然后会改变重链顶的 fa 的 w_0,w_1 值,然后又对应了线段树上的单点修改矩阵,此时又会改变另一个重链顶的 \mathcal{DP} 值……直到根为止。
注意我们求 \mathcal{DP} 数组的时候必须从叶子节点往上走,所以树链剖分的时候不仅要记录链顶还要记录链底。
时间复杂度 O(2^3m \log^2 n)。
有更快的 O(2^3m \log n) 做法,欢迎读者思考。
总结
矩阵优化 \mathcal{DP} 作为信息学竞赛常见套路,必须牢牢掌握。谁也不知道、谁也说不准考点会在哪出现。况且现役选手的水平越来越高,在 NOI2015 出现的树链剖分,现在进入了寻常百姓家;NOIP2018 的保卫王国,则有效普及了动态 \mathcal{DP}。信息学竞赛在这几年内一直蓬勃发展。
对于知识点的学习,在我看来,学习理论只有启蒙作用,要提升自己更应该动手实践敲代码。实际上矩阵优化有很多的实现细节,譬如:时刻注意矩阵只有结合律,没有交换律;当矩阵较小的时候,是否考虑不使用循环来优化程序的常数因子;当模数为 2 时,是否考虑直接用 bitset 优化……诸如此类。只有多接触各类题目、多看大神题解、多向大神请教,我们才能学会这些“奇技淫巧”(可能在别人眼中这只是众人皆知的套路)。
金无足赤,人无完人。希望大家在前进的道路上不断努力,今天多学的东西,总会成为明天的回报。