题解:AT_arc138_f [ARC138F] KD Tree
TruchyR
·
·
题解
一个不一样的做法,不管字典序这种东西。
$f(I_x,I_y)$ 表示只考虑 $x\in I_x$,$y\in I_y$ 的点时能得到的**答案序列**数量,$I$ 代表一个区间。
考虑如何计算 $f([x_l,x_r],[y_l,y_r])$。
先把这里面的点**离散化**一下。然后显然不同的操作序列可能得到相同的答案序列,所以直接做是错的。
那么我们直接容斥,定义 $F(S)$ 为钦定第一步是 $S$ 中任何操作都能到达的答案序列数量,答案即 $\sum\limits_{s\neq \emptyset} (-1)^{|S|-1}F(S)$。
$|S|=1$ 是平凡的,考虑 $|S|=2$ 的情况。
下文说垂直 $x$ 切一刀在 $x_1$ 即在 $x=x_1$ 做一次操作,把点分为 $x\leq x_1$ 和 $x>x_1$ 两部分。
如果垂直 $x$ 轴划两刀在 $x_1<x_2$:
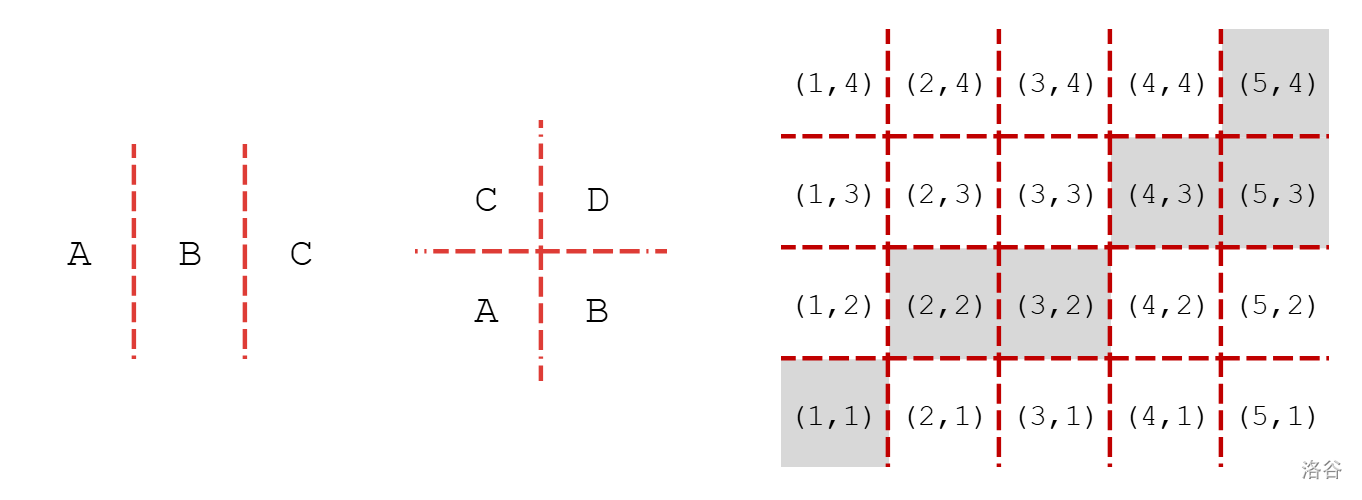
- 所有点被划分成 $A|B|C$ 的样子。
- $x_1$ 得到的序列是 $A+BC$,$x_2$ 得到的序列是 $AB+C$。
- 所以答案序列形如 $A+B+C$。
- 方案数就是 $f([x_l,x_1],I_y)\times f((x_1,x_2],I_y)\times f((x_2,x_r],I_y)$。
垂直于 $y$ 轴同理。
如果一刀垂直 $x$ 轴切在 $x_1$,一刀垂直 $y$ 轴切在 $y_1$:
- 所有点被划分成 $\frac{C}{A}|\frac{D}{B}$ 四个部分。
- $x_1$ 得到的序列是 $AC+BD$,$x_2$ 得到的序列是 $AB+CD$。
- **容易发现 $B$ 和 $C$ 不能同时不为空**。
- 方案数是 $f([x_l,x_1],[y_l,y_1])f([x_l,x_1],(y_1,y_r])f((x_1,x_r],[y_l,y_1])f((x_1,x_r],(y_1,y_r])$。
考虑如何推广到 $|S|>2$。
类似的,如果垂直 $x$ 轴划了 $a$ 刀,垂直 $y$ 轴划了 $b$ 刀,所有点会被划分成 $(a+1)(b+1)$ 部分。我们按照图示方法记录每个部分为一个二元组 $(i,j)$。
根据 $|S|=2$ 的结论,存在至少一个答案序列的条件即**对于任意一个非空部分 $(i_1,j_1)$,所有满足 $i_2<i_1,j_2>j_1$ 和 $i_2>i_1,j_2<j_1$ 的部分都必须是空的**。
上图浅灰色的格子代表该部分非空,它是符合条件的。
这个条件看起来非常好 dp 啊!
设 $g_{x_1,y_0,y_1}$ 表示竖着最后一刀切在 $x_1$,横着最后两刀切在 $y_0$ 和 $y_1$ 的容斥系数。
假设离散化后剩 $m$ 个坐标,有 $f(I_x,I_y)=\sum\limits_{i=0}^{m-1} g_{m,i,m}$。
转移从小到大枚举 $x_1$,再枚举上一刀 $x_0$。开一个辅助转移的数组 $h$。
- 先 $h_{y_0,y_1}\leftarrow -g_{x_0,y_0,y_1}\times f((x_0,x_1],(y_0,y_1])$,代表切一刀竖着的。
- 然后 $h_{y_1,y_2}\leftarrow -h_{y_0,y_1}\times f((x_0,x_1],(y_1,y_2])$,代表切几刀横着的。
记 $c(I_x,I_y)$ 为在范围内的点的数量。为了满足条件且不重不漏,$f_{x_1,y_0,y_1}\leftarrow h_{y_0,y_1}$ 的条件是:
- $c((x_0,x_1],(y_0,y_1])>0$,这是为了不重。
- $c((x_0,x_1],(y_1,y_r])=c((x_1,x_r],[y_l,y_0])=0$,这是为了满足条件。
然后就可以转移了。然后这题就做完了。
关于复杂度,往高了算是 $\sum_{i=1}^{n}\sum_{j=1}^n(n-i+1)(n-j+1)i^2j^2$。
这玩意能分析到 $O(n^8)$,但是常数小的没边完全可以过。
代码中使用的变量名和文章中的略有不同。
::::info[完整代码]
```cpp
#include<bits/stdc++.h>
#define int long long
#define Get(A,B,C,D) f[x[(A)]+1][x[(B)]][y[(C)]+1][y[(D)]]
#define Cnt(A,B,C,D) query(x[(A)],x[(B)],y[(C)],y[(D)])
#define CKE if(CHECK)
#define FRE if(FIL)
using namespace std;
const int mod=1000000007,MX=35;
const int CHECK=0,FIL=0;int read();
bitset<MX> g[MX][MX][MX];
int n,p[MX],fp[MX],a[MX][MX],f[MX][MX][MX][MX],h[MX][MX][MX],H[MX][MX],Hr[MX];
int query(int xl,int xr,int yl,int yr){
return a[xr][yr]+a[xl][yl]-a[xl][yr]-a[xr][yl];}
int solve(int xl,int xr,int yl,int yr){
if(g[xl][xr][yl][yr]) return f[xl][xr][yl][yr];
g[xl][xr][yl][yr]=1;
if(query(xl-1,xr,yl-1,yr)<2){return f[xl][xr][yl][yr]=1;}
vector<int> x,y;
x.emplace_back(xl-1);
for(int i=xl;i<=xr;i++) if(yl<=p[i] && p[i]<=yr) x.emplace_back(i);
y.emplace_back(yl-1);
for(int i=yl;i<=yr;i++) if(xl<=fp[i] && fp[i]<=xr) y.emplace_back(i);
int m=x.size()-1;
for(int xi=0;xi<m;xi++) for(int xj=xi+1;xj<=m;xj++)
for(int yi=0;yi<m;yi++) for(int yj=yi+1;yj<=m;yj++)
solve(x[xi]+1,x[xj],y[yi]+1,y[yj]);
h[0][0][0]=1;
for(int xj=1;xj<=m;xj++){
h[xj][0][0]=0;
for(int yi=0;yi<m;yi++) for(int yj=yi+1;yj<=m;yj++) h[xj][yi][yj]=0;
for(int xi=0;xi<xj;xi++){
H[0][0]=h[xi][0][0];
for(int yj=1;yj<=m;yj++) Hr[yj]=0;
for(int yi=0;yi<m;yi++) for(int yj=yi+1;yj<=m;yj++){
int cnt=h[xi][yi][yj];
if(!yi) cnt-=H[0][0]; else cnt-=Hr[yi];
H[yi][yj]=(cnt%mod)*Get(xi,xj,yi,yj)%mod;Hr[yj]+=H[yi][yj];
if(xi==0 && xj==m && yi==0 && yj==m) H[yi][yj]=0;
if(Cnt(xi,xj,yi,yj) && !Cnt(xi,xj,yj,m) && !Cnt(xj,m,0,yi))
h[xj][yi][yj]=(h[xj][yi][yj]+mod-H[yi][yj])%mod;
}
}
}
int ans=0;
for(int yi=0;yi<m;yi++){
int cnt=h[m][yi][m];
ans=(ans+mod-cnt)%mod;
}
f[xl][xr][yl][yr]=ans;
return f[xl][xr][yl][yr];
}
signed main(){
n=read();
for(int i=1;i<=n;i++){p[i]=read();fp[p[i]]=i;}
for(int i=1;i<=n;i++) a[i][p[i]]++;
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) a[i][j]+=a[i-1][j];
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) a[i][j]+=a[i][j-1];
solve(1,n,1,n);
printf("%lld\n",f[1][n][1][n]);
return 0;
}
int read(){
int Ca=0;char Cr=' ';int Cf=1;
while(Cr<'0' || Cr>'9'){Cr=getchar();if(Cr=='-'){Cf=-1;}}
while(Cr>='0' && Cr<='9'){Ca=Ca*10+Cr-48;Cr=getchar();}
return Ca*Cf;
}
```
::::