初赛复习集
erok
·
·
个人记录
CSP-S重点复习
初赛
- 计算机与 \text{€€£} 发展史(记住一年 n 度的圈钱比赛举行了多少次)
- 各类排序的时间与空间复杂度,稳定性。
- 递推关系式的时间复杂度(主定理)
- 组合数学
- 位运算
- 逻辑运算
- 手模程序
- 进制转换
- 数据结构
- 二叉树
- 计算机的基本构成
- 操作系统的基本概念和常见操作
- 阅读程序能力(理解 €€£ 的 nt 代码)
计算机的基本构成
冯诺依曼结构体系中构成计算机的五大部件 存储器、运算器、控制器、输入设备、输出设备。
中央处理器主要包括两个部分,即控制器、运算器。
运算器由算术逻辑单元(\text{ALU})、累加器、状态寄存器、通用寄存器组等组成。
控制器由程序计数器、指令寄存器、指令译码器、时序产生器和操作控制器组成。
总线是计算机各种功能部件之间传送信息的公共通信干线。
$\text{ROM}$断电后,不受影响。
$\text{RAM}$在计算期间被用作高速暂存记忆区,当计算机在运行时$\text{RAM}$是可得到的,当关闭计算机时信息将会丢失。
$\text{CPU}$的功能主要是解释计算机指令,控制程序以及处理计算机软件中的数据。
# 位运算
取出整数 $n$ 在二进制表示下的第 $k$ 位
取出整数 $n$ 在二进制表示下的第 $0∼k−1$ 位(后 $k$ 位)
对整数 $n$ 在二进制表示下的第 $k$ 位取反
对整数 $n$ 在二进制表示下的第 $k$ 位赋值 $1
对整数 n 在二进制表示下的第 k 位赋值 0
按位与
与常数 0 进行操作
1111 \land 0000=0000
可以发现,对于按位与,只要一个操作位上的数字为 0,结果一定恒为 0。
与常数1进行操作
1000&\\
\underline{\land\ 0001}&\\
0000
\end{aligned}
1111&\\
\underline{\land\ 0000}&\\
0000
\end{aligned}
同样进行推理,对于按位与,只要一个操作位上的数字为 1,结果一定与操作的二进制位相同,即结果对于原来的数字不变。
与常数 0 进行操作
1000&\\
\underline{\lor\ 0000}&\\
1000
\end{aligned}
1111&\\
\underline{\land\ 0000}&\\
1111
\end{aligned}
可以发现,按位或对 0 操作与按位与对 1 进行操作一样。
进行总结:对于按位或,只要一个操作位上的数字为 0,结果一定与操作的二进制位相同,即结果对于原来的数字不变。
操作系统的基本概念和常见操作
$\text{LAN} $局域网
$\text{MAN} $城域网
$\text{Linux}$下的文件不需要扩展名。
操作系统是一组主管并控制计算机操作、运用和运行硬件、软件资源和提供公共服务来组织用户交互的相互关联的系统软件程序。
程序中断是指在计算机执行程序的过程中,出现某些急需处理的异常情况或特殊请求,$\text{CPU}$暂时中止现行程序,而转去这些异常情况或特殊请求进行处理。
$\text{C}$语言 面向过程
$\text{Java, Python, C++}$ 面向对象
# 图论
## 二分图
**定义:将一个图分为两部分,每个部分中的任意两点之间不存在边。**
有$n$个点的二分图最多有$\Large(\frac{n}{2})^2$条边
## 二叉树
前序遍历 根左右
中序遍历 左根右
后序遍历 左右根
前 + 中 → 推出二叉树
中 + 后 → 推出二叉树
## 特殊的二叉树及其性质
满二叉树/完美二叉树:
所有叶结点的深度均相同的二叉树称为满二叉树/完美二叉树。
完全二叉树:只有最下面两层结点的度数可以小于 $2$,且最下面一层的结点都集中在该层的最左侧。
# 数据结构
## 链表
**定义:链表和数组都可用于存储数据,其中链表通过指针来连接元素,而数组则是把所有元素按次序依次存储。**
链表可以方便地删除、插入数据,操作次数是 $O(1)$,但是访问任意数据时操作次数是 $O(n)$。
**链表不可以随机访问任意数据!**
## 字符串
**定义:字符串指一串字符组成的串。**
**子串:子串被定义为字符串中任意个连续的字符组成的子序列**.
子串个数 $=\large\frac{n(n+1)}{2}+1$.
非空子串的个数 $=\large\frac{n(n+1)}{2}$.
无非就是少了空子串的$+1
递推式的时间复杂度
主定理
T(n)=aT(\lceil{\frac{n}{b}}\rceil)+O(n^d)
\text{(for constants $a>0,b>1,d\ge0$),then$:$}
O(n^d)&{if}\quad{d>{\log_b}\ a}\\
O(n^d{\log\ }n)&{if}\quad{d={\log_ba}}\\
O(n^{\log_ba\ })&{if}\quad{d<{\log_ba}}
\end{cases}
数学
最大公约数与最小公倍数
辗转相除法(欧几里得算法)
每次取除数和余数进行反复除法运算,当余数为零,除数即为最大公约数。
组合数学
排列
定义:从 n 个不同元素中,任取 m 个元素按照一定的顺序排成一列,读做从 n 个不同元素中取出 m 个元素的一个排列
A(m,n)=n!/(n-m)!
组合
定义:从 n 个不同元素中,任取 m 个元素组成一个集合,读做从 n 个不同元素中取出 m 个元素的组合。即不关心被选元素的顺序
C(m,n)=n!/m!(n-m)!
一些方法
-
先选后排:先将元素选出来,再进行排列,非常有效的降低问题的复杂度。
-
特殊优先:特殊元素,优先处理;特殊位置,优先考虑。
-
分排用直排:n个元素,从中选出 m个,将这 m 个元素排成若干排。分排问题的排列可以看做一排,避免考虑了复杂的前后排列,简化了问题。
-
分类法:当计算符合条件的数目比计算不符合条件数目简单时,将问题分成若干类,逐个求解,与“排除法”相对。
-
排除法:当计算符合条件的数目比计算不符合条件数目复杂时,简称正难则反。排除不符合要求的,剩下的就是符合题目要求的。与“分类法”相对。
-
捆绑法:n 个不同元素排成一列,要求 m个元素必须相邻。可以特殊优先,把 m 个元素捆绑在一块单独处理。S=A_{n-m+1}^{n-m+1}×A_m^m.
-
插空法:n 个不同元素排成一列,要求 m 个元素不能相邻。先把不用特殊处理的元素进行排列,再把甲乙进行插空。 S=A_{n-m}^{n-m}×A^m_{n-1}.
-
隔板法/插板法:将 n 个相同元素分成 m 组,每组至少有一个元素。相当于把 m−1 个隔板插到 n 个元素形成的 n-1 个空隙里。S=C_{m-1}^{n-1}.
-
定序: n 个元素的全排列中有 m 个元素必须定序排列,这 m 个元素相邻或不相邻不受限制。 \large S=\frac{A^n_n}{A^m_m}.
-
错排递推式 S_i=(i-1)*(S_{i-1}+S_{i-2}),S_1=0,S_2=1;
进制
10进制转n进制 整数部分,辗转除 n,取余。小数部分,辗转乘 n,取整数部分。
n进制转十进制 第i位*n并相加即可。
关于CCF与各项竞赛
复赛使用 C、C++、Pascal,2022 年后只能使用 C++。
复赛使用 NOI Linux 评测。
NOI(National Olympiad in Informatics):全国青少年计算机程序设计竞赛,开办于 1984 年,现更名全国青少年信息学奥林匹克竞赛。
NOIP(National Olympiad in Informatics in Provinces):全国青少年信息学奥林匹克联赛, 自 1995 年至 2018 年已举办 24 次。复赛可使用 C、C++、Pascal 语言,2022 年后只能使用 C++。 2019 年,由于某种原因, NOIP 暂停 ,在 2020 年恢复。
特别的,如果题目询问了 NOIP 举办了多少届,需要扣除一届,因为 CSP 举行的时候 NOIP 还没有举行。
APIO(Asia-Pacific Informatics Olympiad):亚洲与太平洋地区信息学奥林匹克竞赛。
IOI(International Olympiad in Informatics):国际信息学奥林匹克竞赛,等级最高的信息学竞赛。
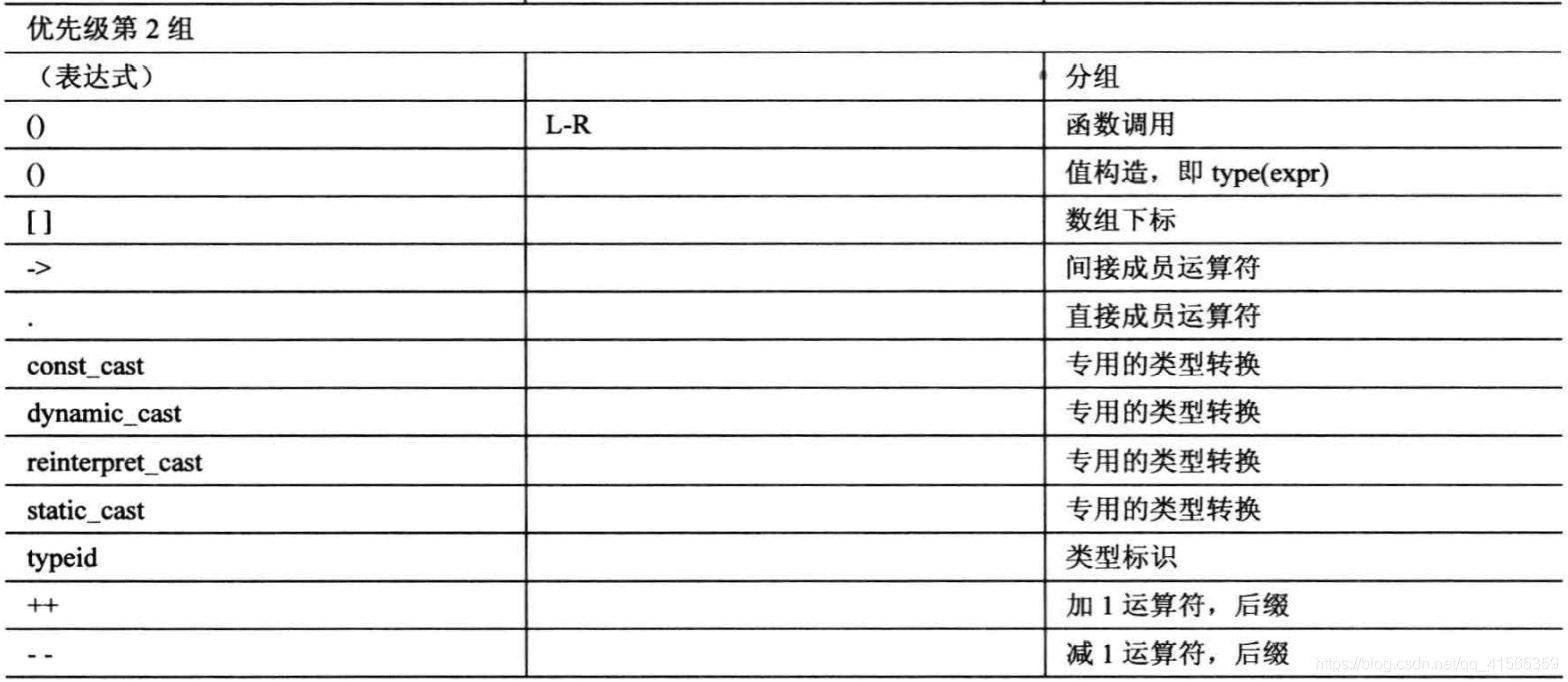
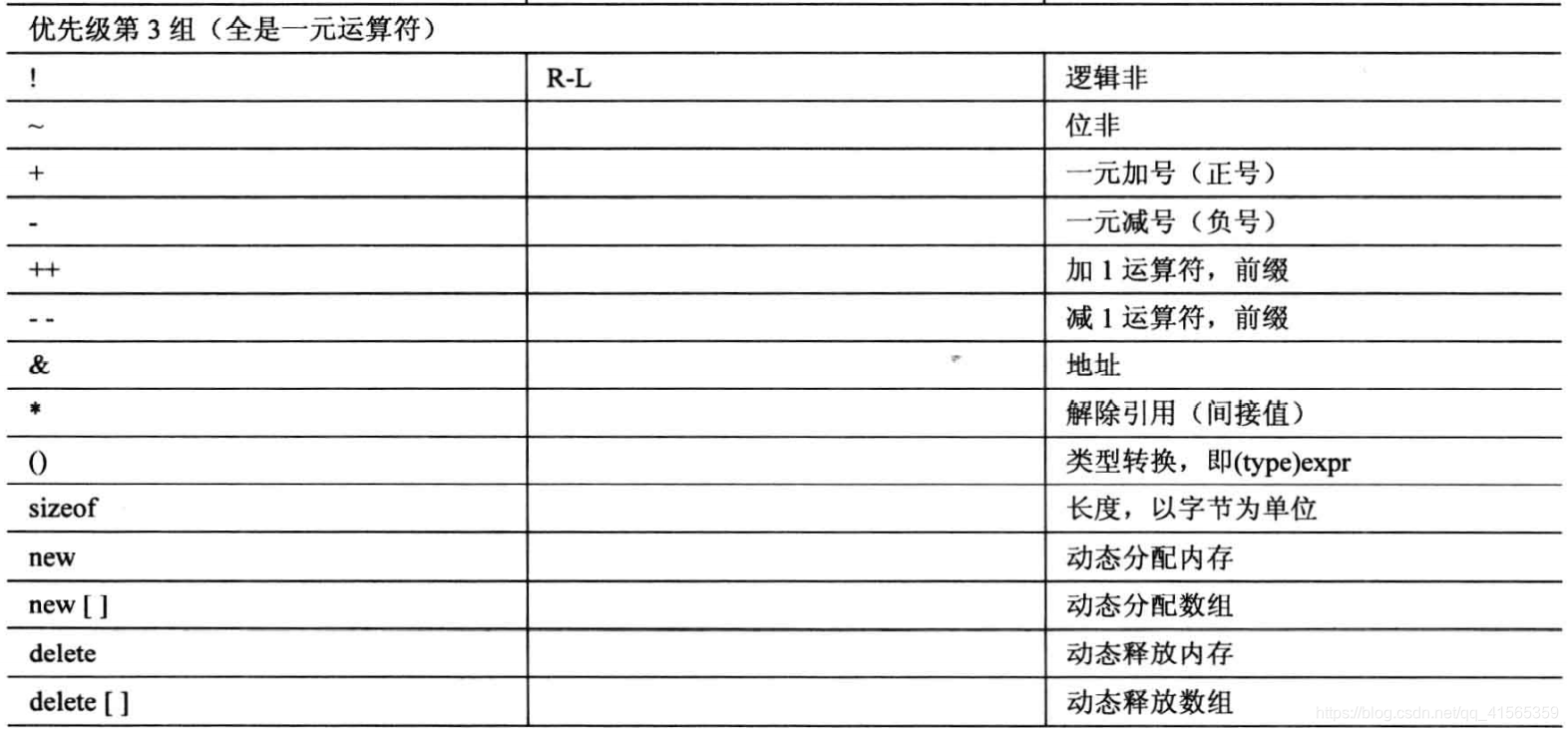
## 各类运算符优先级汇总






# 以及最重要的——
# 信心
$$\boxed{\begin{matrix}
\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}\\
\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}\\
\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\\
\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\\
\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\\
\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\\
\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\\
\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\\
\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\\
\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\\
\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\text{逢考必过}&\\
\end{matrix}}
$$
# 祝看到这篇博文的你,统统AK!!!
部分资料 by [159号程序员](https://www.luogu.com.cn/blog/334586/csp-pre-knowledge)
运算符优先级汇总by[CSDN](https://blog.csdn.net/qq_41565359/article/details/113878104)
鸣谢 :[khm314](https://www.luogu.com.cn/user/633886) 调整了LaTeX格式 。
本博文仅做记录与个人复习用,请勿发布任何意见。文明阅读,备考顺利。