AC自动机:从入门到入坟
_Cheems
·
·
个人记录
前言
首先初步理解自动机的概念吧:链接在这。
### 自动机构建
大体描述为:字典树 $+$ $\rm kmp$(思想上),于是可分两部分。
第一部分:将所有模式串构成一棵字典树,不解释。但是强调字典树上一点的含义:表示根到该点路径上所有字符构成的串,称其为 $S(i)$,它必定是某个模式串前缀。
第二部分:失配数组 $fail$,即 $i\to fail_i$ 构成的边。
接下来解释 $fail_i$ 的含义:$S(fail_i)$ 是 $S(i)$ 的最长后缀,注意 $i\ne fail_i$。
考虑广搜求出 $fail$,假设当前遍历到点 $u$,则深度 $<u$ 的节点均已求出 $fail$ 值,我们将像 $\rm kmp$ 一样由先前的 $fail$ 推导出现在的 $fail$。
补充一点:一个串的最长后缀的最长后缀也是该串的后缀,于是我们不断沿着 $fail$ 边向根走就能不重不漏遍历到 $S(i)$ 的所有后缀,这句话很重要,类比 $\rm border$ 理解。
设 $v$ 是字典树上点 $u$ 走 $c$ 边到达的点,即 $v = trie_{u,c}$,显然 $S(v)=S(u)+c$。
那么我们不断寻找 $u$ 的后缀(跳 $fail$)来尝试匹配,设当前在点 $p$,那么形式化地说:
1. $p$ 初始化为 $u$。
2. 若 $trie_{fail_p,c}$ 不为空,则 $fail_v$ 指向 $trie_{fail_p,c}$,否则使 $p=fail_p$。
3. 重复寻找直到 $p=0$。
来看具体实现:
```cpp
inline void ins(char a[], int m){
int u = 0;
for(int i = 1, c; i <= m; ++i){
c = a[i] - 'a';
if(!trie[u][c]) trie[u][c] = ++tot;
u = trie[u][c];
}
}
inline void build(){
queue<int>q;
for(int i = 0; i < 26; ++i)
if(trie[0][i]) q.push(trie[0][i]);
while(!q.empty()){
int u = q.front(); q.pop();
for(int i = 0, v; i < 26; ++i){
v = trie[u][i];
if(v) fail[v] = trie[fail[u]][i], q.push(v);
else trie[u][i] = trie[fail[u]][i];
}
}
}
```
解释下 `build` 部分求解失配数组为啥这样写:发现暴力跳 $fail$ 是相当低效的,如果我们能在当前点记录下跳 $fail$ 的最终结果,那么下次跳到该点时就能直接得到答案了。
于是,当 $v$ 不为空时,直接按照理论得出 $fail_v$ 的值;当 $v$ 为空时,让 $v$ 指向 $u$ 所在 $fail$ 链最近的一个实点。没看懂不要紧,看下图:
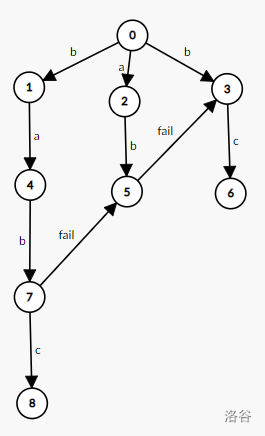
我们遍历到点 $5$ 的虚点 $trie_{5,c}$,为了优化复杂度,直接让 $trie_{5,c}$ 指向 $trie_{fail_5,c}$,即点 $6$:
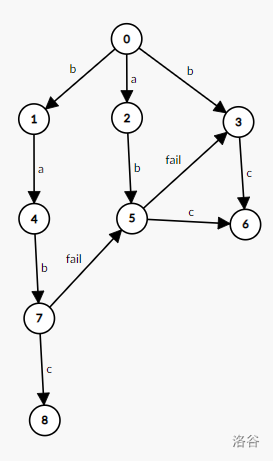
于是当我们遍历到 $7$ 的 $c$ 节点时,便会跳到 $trie_{fail_7,c}$,即点 $6$,就能做到直接跳至目标状态。
至此,完成了自动机构建,复杂度线性。
注意一个细节:不能直接从根开始跑 bfs,否则根的儿子会出现 $fail_i=i$ 的情况。
### 文本串在自动机上的查询
直接将文本串 $T$ 放在 $\rm trie$ 上跑,每到一个节点不断跳 $fail$,看看它是否是某个模式串的结尾。这样实质上是高效遍历 $S(i)$ 的后缀并匹配,最终相当于遍历 $T$ 的所有子串。
解答一个问题:假如跑到一半匹配不了了怎么办?即 $trie_{u,T_i}=0$ 时怎么办?由于我们在构建 $fail$ 时让空指针也指向了一个值,因此实际上 $trie_{u,T_i}$ 会指向一个在 $\rm trie$ 中存在的、是 $T[0,i]$ 后缀的最长状态。形象化地说,我们舍弃了 $T$ 的部分前缀,这显然不会影响答案,并使得匹配可以继续进行。
### 查询的优化——拓扑排序
上述过程比较低效,我们没有必要每次都跑完一条 $fail$ 链,只要对其标记即可。
于是考虑如下优化:把 $T$ 放在 $\rm trie$ 上跑,并标记跑过的点 $i$,记 $cnt_i+1$。然后将失配边($i\to fail_i$)拎出来建图,跑拓扑排序更新 $cnt$。
当然不必真的建图,只要在构建自动机时计算入度即可。
不难发现最终 $cnt_i$ 表示 $S(i)$ 在 $T$ 中出现了几次,复杂度线性。
### 板子
可过 [P5357 【模板】AC 自动机](https://www.luogu.com.cn/problem/P5357) 的加强数据。
```cpp
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5, M = 2e6 + 5, C = 30;
int n;
char s[M];
namespace acam{
int trie[N][C], tot, id[N], rev[N], fail[N], in[N], cnt[N];
inline void ins(char a[], int m, int d){
int u = 0;
for(int i = 1, c; i <= m; ++i){
c = a[i] - 'a';
if(!trie[u][c]) trie[u][c] = ++tot;
u = trie[u][c];
}
rev[d] = u;
}
inline void build(){
queue<int>q;
for(int i = 0; i < 26; ++i)
if(trie[0][i]) q.push(trie[0][i]);
while(!q.empty()){
int u = q.front(); q.pop();
++in[fail[u]];
for(int i = 0, v; i < 26; ++i){
v = trie[u][i];
if(v) fail[v] = trie[fail[u]][i], q.push(v);
else trie[u][i] = trie[fail[u]][i];
}
}
}
inline void query(char a[], int m){
int u = 0;
for(int i = 1, c; i <= m; ++i){
c = a[i] - 'a';
u = trie[u][c], ++cnt[u];
}
}
inline void topo(){
queue<int>q;
for(int i = 0; i <= tot; ++i)
if(!in[i]) q.push(i);
while(!q.empty()){
int u = q.front(), v; q.pop();
v = fail[u];
cnt[v] += cnt[u];
if(!(--in[v])) q.push(v);
}
}
}
using namespace acam;
signed main(){
cin >> n;
for(int i = 1; i <= n; ++i){
scanf("%s", s + 1);
ins(s, strlen(s + 1), i);
}
build();
scanf("%s", s + 1);
query(s, strlen(s + 1)), topo();
for(int i = 1; i <= n; ++i)
printf("%d\n", cnt[rev[i]]);
return 0;
}
```
### 板子例题
都是比较板的。
#### P3121 [USACO15FEB] Censoring G
借鉴 [P4824](https://www.luogu.com.cn/problem/P4824) 的思路,用个栈扫一遍,实时维护当前串对应在 $\rm trie$ 上的下标,期间每加入一个元素就进行一次匹配,匹配成功就删去、退栈即可。
关于匹配,可以离线维护 $fail$ 链上一段的最小值即可,复杂度线性。