网络流
liushuangning
·
2025-01-19 11:14:43
·
算法·理论
本蒟蒻第一次学网络流,如果有错误,欢迎各位大佬指出!
基础与定义
流网络
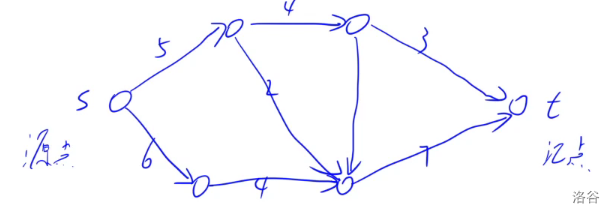
其中 $s$ 为源点,$t$ 为汇点,边上的数字为容量。
## 可行流
### 定义
可行流表示为 $f$,$c$ 为容量。一个可行流 $f$ 要满足容量限制和流量守恒两条限制。
- 容量限制:
$$
0\le f(u,v)\le c(u,v)
$$
- 流量守恒:
$$
\forall x\in V-\{s,t\},\sum_{(v,x)\in E}f(v,x)=\sum_{(x,v)\in E}f(x,v)
$$
定义 $|f|$ 为可行流 $f$ 的流量值。
$$
|f|=\sum_{(s,v)\in E}f(s,v)-\sum_{(v,s)\in E}f(v,s)
$$
### 举例
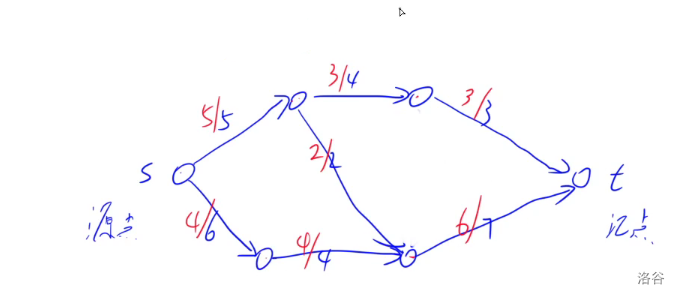
这样的就是一个可行流,比较每个点(不包括源点和汇点)流出的流量和流入的流量,发现它们是相等的,且每条边的流量不超过容量。
**注意:一个图中可能有很多的可行流。**
最大流:一个集合里流量最大的一个**可行流**。
### 加减法
一个流网络中两个可行流的加法就是对应边相加,减法类似。
### 流的分解定理
任意可行流 $f$ 均可以分解为有限个从源到汇的路径和环的组合。
## 残留网络
定义:
$V_f=V,E_f=E+E_{\text{rev}}
c'(u,v)=
\begin{cases}
c(u,v)-f(u,v)&&&(u,v)\in E\\
f(v,u)&&&(v,u)\in E
\end{cases}
记作 G_f 。
残留网络是和可行流一一对应的,可行流不同,残留网络也不同。
像这两个流网络,下面的就是上面的残留网络。
$|f+f'|=|f|+|f'|
增广路径
定义:在残留网络里面,从源点出发,沿着容量大于 0 的边,如果能够走到汇点的话,那么这条路径就被称为增广路径。
若流网络 G 的一条可行流 f 的残留网络 G_f 中不存在增广路径的话,那么 f 就是 G 的最大流。
割
定义
将点集 V 分成两个集合 S,T ,使得 S\cup T=V,S\cap T=\varnothing ,且 s\in S,t\in T 。
容量
所有从 S 指向 T 的边的容量之和。
c(S,T)=\sum_{u\in S}\sum_{v\in T}c(u,v)
注意:只算从 S 指向 T 的边。
最小割:割的容量最小的那一种分割方案。
分割方案数:2^{n-2} 种。
流量
f(S,T)=\sum_{u\in S}\sum_{v\in T}f(u,v)-\sum_{u\in T}\sum_{v\in S}f(u,v)
性质:\forall[S,T]\forall f
所以最大流 \le 最小割。
最大流最小割定理
对于某一个流网络 G(V,E) ,以下三个条件是等价的:
最大流
算法模板
EK 算法
while( ){
1.找增广路径(BFS)
2.更新残留网络
}对于更新残留网络:
时间复杂度:O(nm^2) 。
但是
yxc:网络流算法的时间复杂度跟放屁一样,它的实际效率是非常高的。
存图:第 0 条边是正向边,第 1 条边是第 0 条边的反向边,以此类推。
如果要找 i 这条边的反向边就是 i\oplus 1 。
参考代码(根据此题写的代码,如果你没有买课,这里是题面):
唐氏马蜂,请勿吐槽。
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=1010,M=20010,inf=0x3f3f3f3f;//这里的inf只要比10000大就行
int n,m,S,T;
int h[N],e[M],ne[M],f[M],idx;//f为容量
int q[N],d[N],pre[N];//d为从起点走到当前点的所有边上的容量最小值,pre为前驱边
bool st[N];
void add(int a,int b,int c){
//建正向边
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
//建反向边
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(st,0);
q[0]=S;
st[S]=true;
d[S]=inf;
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i/*等价于i!=-1*/;i=ne[i]){
int ver=e[i];
if(!st[ver] && f[i]>0){
st[ver]=true;
d[ver]=min(d[t],f[i]);
pre[ver]=i;
if(ver==T) return true;//找到了增广路径
q[++tt]=ver;
}
}
}
return false;
}
int EK(){
int r=0;
while(bfs()){
r+=d[T];
for(int i=T;i!=S;i=e[pre[i]^1]/*这条边的编号为pre[i],反向边就是pre[i]^1,反向边指向的点的编号就是e[pre[i]^1]*/){
f[pre[i]]-=d[T];
f[pre[i]^1]+=d[T];
}
}
return r;
}
int main(){
cin>>n>>m>>S>>T;
mems(h,-1);
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
cout<<EK();
return 0;
}注:如果你想在洛谷上 AC 此题,请开 long long,并扩大 inf。
dinic 算法
原题,转存。
EK 算法每次只会搜索流网络中的一条增广路径,但是一个流网络中可能有很多增广路径,dinic 算法的优化思路就是每次将所有增广路径全部搜索一遍。
但是如果有环的话,dinic 算法就会死循环,所以我们引入了分层图 的概念。
也就是说,我们把一张图做成一层一层的,并严格要求每次在寻找增广路径的时候,从起点开始,只能从前一层走到后一层,直到走到终点 ,这样就会保证一定没有环路。
这个点的层数我们定义为到起点的最短距离。
所以 dinic 算法的思路就是:
BFS,建立分层图;
DFS,在分层图中搜索全部增广路径。
当前弧优化:
假设现在已经建立完分层图,那么我们维护从起点到这个点可流过流量的最大值,也就是容量的最小值,当这个点继续往后搜的时候,再看一下从这个点到终点的所有路径中,最多可以流过多少流量,再比较它的一条临边到终点能流过的流量,如果这条边能流过的流量已经满了的话,那么以后枚举到这个点的时候就不需要再枚举这条临边了。
我们用水管来理解,比如这个节点相邻的一条水管已经满了的话,那么考虑方案的时候就不用再考虑这条水管了。
注:dinic 对优化是极其敏感的,如果一个优化写错了,或者少写一个优化都有可能 TLE。
参考代码:
//与EK算法相同的地方不再写注释
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=10010,M=200010,inf=0x3f3f3f3f;
int n,m,S,T;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];//d为分层图层数,cur为当前弧优化,表示当前这个点的第一个没有满的临边
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];//当前弧初始化成第一条边
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;//更新最短距离,be like SPFA
cur[ver]=h[ver];//更新这个点的当前弧
if(ver==T) return true;//找到了增广路径
q[++tt]=ver;
}
}
}
return false;
}
int find(int u/*从u这个点开始搜*/,int limit/*从起点能够流向u这个点的最大流量*/){
if(u==T) return limit;
int flow=0;//表示从u这个点向后流过最大的流量
for(int i=cur[u];~i && flow<limit/*后面流的最大流量要保证小于前面流过的最大流量,如果等于的话,也就没有必要再搜索了*/;i=ne[i]){
cur[u]=i;//将当前弧设为i,因为i之前的边已经满了,否则不会搜到i这条边
int ver=e[i];
if(d[ver]==d[u]+1/*按分层图的顺序*/ && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[ver]=-1;//如果当前这个点不可用(可流过的流量为0),就把这个点删掉
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())//bfs函数即可以建立分层图,还可以返回有没有增广路径
while(flow=find(S,inf)) r+=flow;//如果有增广路径,就在当前的分层图中累加全部增广路径的流量,如果不套while的话,有时会因为inf太小榨不干
return r;
}
int main(){
cin>>n>>m>>S>>T;
mems(h,-1);
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
cout<<dinic();
return 0;
}放屁时间复杂度:O(n^2m) 。
应用概括
问:给我们一个问题 P ,该如何把它转化为一个流网络 G 呢?
我们要证明下面两个条件:
证明完这两个条件后,问题 P 中可行解的最大值 就可以转化成流网络 G 中的最大流 。
如果要求最小解 ,就可以对应到最小割 。
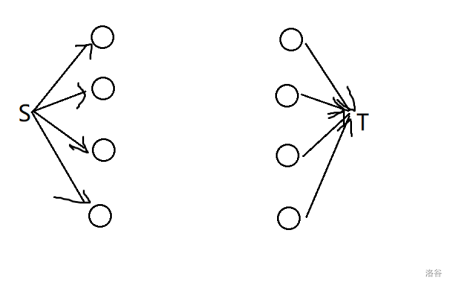
二分图
原题,洛谷原题。
相比较我们之前学过的二分图最大匹配算法,最大流算法会更快。
比如说比较匈牙利算法和 dinic 算法。
匈牙利算法时间复杂度:O(nm) 。
dinic 算法时间复杂度:O(m\sqrt{n}) 。
那么问题来了:用网络流解决二分图最大匹配,要怎么建图呢?
比如给了我们两个点集 V_1 和 V_2 ,就可以这样建图:
建立一个虚拟源点 S ,并向点集 V_1 的每一个点连一条容量为 1 的边。
建立一个虚拟汇点 T ,并将点集 V_2 的每一个点向 T 连一条容量为 1 的边。
对于两个点集之间的边,就连一条容量为 1 的边。
注意:这里的前提是流量为整数,否则可行流不能对应到可行解。
但是我们要求的整数值最大流的集合,是在整个最大流集合内的,也就是说,我们要求的答案是算法给出来的答案的子集。
对于这种情况,我们自习观察一下我们的 dinic 算法,发现我们用过的变量都是整数值变量,所以我们求的可行流,也就都是整数值可行流(这很显然,各位大佬应该不用想就知道)。
参考代码:
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=110,M=5210,inf=0x3f3f3f3f;
int n,m,S,T;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
int main(){
cin>>m>>n;
S=0,T=n+1;
mems(h,-1);
for(int i=1;i<=m;i++) add(S,i,1);
for(int i=m+1;i<=n;i++) add(i,T,1);
int a,b;
while(scanf("%d%d",&a,&b) && a!=-1) add(a,b,1);
cout<<dinic()<<endl;
for(int i=0;i<idx;i+=2)//枚举所有正向边
if(e[i]>m && e[i]<=n && f[i]==0) printf("%d %d\n",e[i^1],e[i]);//这条边在两个点集中间,且正向边的流量为0(被选了)
return 0;
}原题,洛谷原题。
对于这道题,我们知道 m 个单位,n 个圆桌,每个单位的人数分别是 r_1,r_2,...,r_m ,每个圆桌的容量分别是 c_1,c_2,...,c_n 。
要求:每张圆桌上,不能有两个人在同一个单位。
这题还是一道二分图的问题,m 个单位可以画 m 个点,n 张圆桌可以画 n 个点,左边每个点向右边每个点连一条容量为 1 的边。
但是这题的特殊之处就在于:每个点可以选多次。比如说第一个单位有两个人,那么这个点是可以在两条边里的。也就是说,有些边是可以共用某些点的。这道题就是二分图的多重匹配问题。
我们可以参考上一题的建图方式,建立源点和汇点,源点向左边每个点连一条容量为 r_i 的边(因为这个点可以用 r_i 次),右边每个点向汇点连一条容量为 c_i 的边。
下面是一种情况:
题目要求我们输出一种方案,使得所有代表都有地方坐,也就是从源点出发的边都是满流 。
那么问题有没有解,就相当于流网络存不存在一条可行流,使得从源点出发的边都是满流。其实就是看一下流网络的最大流,从源点出发的边是不是都是满流。
也就是计算最大流是不是等于总人数。
输出方案的时候,只要看一下从左边出发的每条边,哪些边是满流的,就说明左边这个单位向右边那张桌子派了一名代表。
参考代码:
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=430,M=(150*270+N)*2,inf=0x3f3f3f3f;
int m,n,S,T;
int h[N],e[M],f[M],ne[M],idx;
int q[N],d[N],cur[N];
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
int main(){
cin>>m>>n;
S=0;
T=m+n+1;
mems(h,-1);
int tot=0;//总人数
for(int i=1;i<=m;i++){
int c;
scanf("%d",&c);
add(S,i,c);
tot+=c;
}
for(int i=1;i<=n;i++){
int c;
scanf("%d",&c);
add(i+m,T,c);
}
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++) add(i,j+m,1);
if(dinic()!=tot) puts("0");//无解
else{
puts("1");
for(int i=1;i<=m;i++){
for(int j=h[i];~j;j=ne[j])
if(e[j]>m && e[j]<=m+n && !f[j]) printf("%d ",e[j]-m);
puts("");
}
}
return 0;
}上下界可行流
无源汇上下界可行流
原题,转存。
原先的流量要满足的条件是:0\le f(u,v)\le c(u,v) 。
现在的流量要满足的条件是:c(u,v)\le f(u,v)\le d(u,v) 。
为了方便,下面把 c(u,v) 叫做 c_l(u,v) ,d(u,v) 叫做 c_u(u,v) 。
设原网络是 G ,原网络的一条可行流是 f ,我们希望把 (G,f) 变成 (G',f') ,使得 G' 符合我们平时见到的流网络。
原网络的条件为:c_l(u,v)\le f(u,v)\le c_u(u,v) 。
将每一项都减去 c_l(u,v) ,得:0\le f(u,v)-c_l(u,v)\le c_u(u,v)-c_l(u,v) ,这样就是我们平常见到的流网络的流量限制了。
然后我们再将求出来的方案加上 c_l(u,v) ,这样得到的流网络满足容量限制,但是不一定满足流量守恒,比如说这样的一个局部:
每条边的容量都加上 c_l(u,v) 的话,就会将进入的流量多减 C_{\text{out}}=\sum_{v\in V} c_l(x,v) ,多加 C_{\text{in}}=\sum_{v\in V} c_l(v,x) ,很有可能这个点出去的流量和进入的流量不相等。
其实我们只要从源点或汇点连一条边补上流量就可以了,如果 C_{\text{out}}>C_{\text{in}} ,只需要从源点连一条流量为 C_{\text{out}}-C_{\text{in}} 的边,那么现在的流量就守恒了。
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=210,M=(10200+N)*2,inf=0x3f3f3f3f;
int n,m,S,T;
int h[N],e[M],f[M],l[M],ne[M],idx;
int q[N],d[N],cur[N],A[N];//A[i]表示这个点进入的容量下界之和-出去的容量下界之和
void add(int a,int b,int c,int d){
e[idx]=b;
f[idx]=d-c;
l[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(!t) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
int main(){
cin>>n>>m;
S=0;
T=n+1;
mems(h,-1);
for(int i=0;i<m;i++){
int a,b,c,d;
scanf("%d%d%d%d",&a,&b,&c,&d);
add(a,b,c,d);
A[a]-=c;
A[b]+=c;
}
int tot=0;//从源点出发到每个点的容量下界之和
for(int i=1;i<=n;i++){
if(A[i]>0){
add(S,i,0,A[i]);//从源点连边
tot+=A[i];
}
else if(A[i]<0)
add(i,T,0,-A[i]);//向汇点连边
}
if(dinic()!=tot) puts("NO");//不是满流,就说明无解
else{
puts("YES");
for(int i=0;i<m*2;i+=2) printf("%d\n",f[i^1]+l[i]);
}
return 0;
}有源汇上下界最大流
原题,转存。
这题规定了源点和汇点,从上一题的所有点都是流量守恒(不算自己增加的点),变成了除了源点和汇点,都是流量守恒。为了解决这个问题,我们可以从汇点向源点连一条容量为 +\infty 的边。
问:如何求最大流?
我们很容易想到下面的做法:先按上一题的做法转换流网络,并删掉那条刚加的边,再做一遍 dinic,就可以保证 s 到 t 没有增广路径,所以就求出了最大流。
但是 这个证明是错误的,因为我们求出的残留网络是从 S 到 T 的残留网络,而我们要求的是从 s 到 t 的最大流,所以不能这样想。
我们选择原图 G 的一条可行流 f_0 ,通过之前的变换,成为图 G' 中特定的一条可行流 f_0' ,然后求一下 f_0' 的残留网络 G'_{f_0'} ,那么这个残留网络中 S 到 T 的满流就是 f_0' ,那么这个可行流里面有一部分的流就是从 s 到 t 流过去的,流量就是之前加上的那条从 t 到 s 的流量,记为 f_{0\ s\rarr t}' ,下面我们从 G'_{f_0'} 中找到所有 s 到 t 的可行流(右),再找到原图的所有 可行流(左),我们只需要证明这两个集合中的可行流一一对应。
我们可以这样证明:左集合中任意一个元素可以在右集合中找到,右集合中的任意一个元素也可以再左集合中找到。
右到左:现在从右集合任取一个可行流,记为 f'_{s\rarr t} ,那么不难发现 f'_{s\rarr t}+f_0' 仍然是一个 G' 的满流,也就是原图的一条可行流,所以说右边集合的任意一个元素可以找到左边集合的一个元素对应。
左到右:首先左集合的一条可行流 f 通过变换可以得到 G' 中的一个满流 f' ,因为 G' 中的所有流都是满流,所以 f'-f_0' 中从 S 出发的所有边和流向 T 的所有边的流量都是 0 ,所以说所有的流量都在中间部分,也就是 s 到 t 的流量,那么左集合中的所有元素就可以对应到右集合的所有元素。
结论:如果要求左集合的最大值就相当于在右集合中求最大值。
如果要求最小流的话就是让 s 到 t 的流尽可能小,也就是让 t 到 s 的流尽可能大,就是求 t 到 s 的最大流。
参考代码:
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=210,M=(N+10000)*2,inf=0x3f3f3f3f;
int n,m,S,T;//S,T是虚拟的源汇
int h[N],e[M],f[M],ne[M],idx;
int q[N],d[N],cur[N],A[N];
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
int main(){
int s,t;//题目给定的源汇
cin>>n>>m>>s>>t;
S=0,T=n+1;
mems(h,-1);
while(m--){
int a,b,c,d;
scanf("%d%d%d%d",&a,&b,&c,&d);
add(a,b,d-c);
A[a]-=c;
A[b]+=c;
}
int tot=0;
for(int i=1;i<=n;i++){
if(A[i]>0){
add(S,i,A[i]);
tot+=A[i];
}
else if(A[i]<0) add(i,T,-A[i]);
}
add(t,s,inf);
if(dinic()<tot) puts("No Solution");
else{
int ans=f[idx-1];//上面加的那条边的流量(因为满流,所以流量等于容量)
S=s;
T=t;
f[idx-1]=f[idx-2]=0;//删边
cout<<ans+dinic();
}
return 0;
}有源汇上下界最小流
原题,转存。
参考代码:
```cpp
#include<bits/stdc++.h>
#define int long long
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=50010,M=(N+125003)*2,inf=1e18;
int n,m,S,T;
int h[N],e[M],f[M],ne[M],idx;
int q[N],d[N],cur[N],A[N];
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
signed main(){
int s,t;
cin>>n>>m>>s>>t;
S=0;
T=n+1;
mems(h,-1);
while(m--){
int a,b,c,d;
scanf("%lld%lld%lld%lld",&a,&b,&c,&d);
add(a,b,d-c);
A[a]-=c;
A[b]+=c;
}
int tot=0;
for(int i=1;i<=n;i++){
if(A[i]>0){
add(S,i,A[i]);
tot+=A[i];
}
else if(A[i]<0) add(i,T,-A[i]);
}
add(t,s,inf);
if(dinic()<tot) puts("No Solution");
else{
int ans=f[idx-1];
S=t;
T=s;//反向求最大流
f[idx-1]=f[idx-2]=0;
cout<<ans-dinic();
}
return 0;
}
```
## 多源汇最大流
[原题](https://www.acwing.com/problem/content/2236/),[转存](https://www.luogu.com.cn/paste/awn6jnz5)。
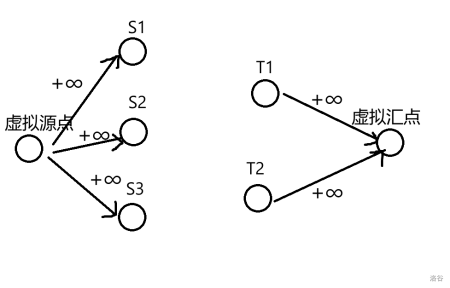
见图知思路,对于刚刚学完上下界的我们来说,这就是易如反掌。(
参考代码:
```cpp
#include<bits/stdc++.h>
#pragma GCC optimize(3,"Ofast","inline")
#define endl '\n'
#define mems(a,b) memset(a,b,sizeof a)
#ifdef PII
#define x first
#define y second
#endif
using namespace std;
template<typename T>
using _heap=priority_queue<T,vector<T>,greater<T>>;
const int N=10010,M=(100000+N)*2,inf=0x3f3f3f3f;
int n,m,S,T;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
int main(){
int sc,tc;
cin>>n>>m>>sc>>tc;
S=0,T=n+1;
mems(h,-1);
while(sc--){
int x;
scanf("%d",&x);
add(S,x,inf);
}
while(tc--){
int x;
scanf("%d",&x);
add(x,T,inf);
}
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
cout<<dinic();
return 0;
}
```
## 关键边
[原题](https://www.acwing.com/problem/content/2238/),[转存](https://www.luogu.com.cn/paste/ov7o5exk)。
抽象化题意:求有多少条边的容量变大后,整个流网络的最大流也会变大。
1. 求最大流 $f$。
2. 若 $f(u,v)=c(u,v)$,且在残留网络 $G_f$ 中,存在从 $S$ 到 $u$ 的路径和从 $v$ 到 $T$ 的路径,那么答案++(路径:沿着剩余容量不等于 $0$ 的边)。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=510,M=10010,inf=0x3f3f3f3f;
int n,m,S,T;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];
bool viss[N],vist[N];//viss表示在残留网络中,是否存在S到u的路径,vist同理
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=1;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]){
int t=find(ver,min(f[i],limit-flow));
if(!t) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
void dfs(int u/*枚举到的点*/,bool st[],int t/*是否用反向边*/){
st[u]=true;
for(int i=h[u];~i;i=ne[i]){
int j=i^t,ver=e[i];
if(f[j] && !st[ver]) dfs(ver,st,t);//容量不等于0,且没走到过
}
}
int main(){
cin>>n>>m;
S=0;
T=n-1;
mems(h,-1);
for(int i=1;i<=m;i++){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
dinic();
dfs(S,viss,0);
dfs(T,vist,1);
int ans=0;
for(int i=0;i<m*2;i+=2)
if(!f[i] && viss[e[i^1]] && vist[e[i]]) ans++;
cout<<ans;
return 0;
}
```
## 最大流判定
[原题](https://www.acwing.com/problem/content/2279/),[洛谷原题](https://www.luogu.com.cn/problem/P1674)。
概括:给你一个 $N$ 个点,$P$ 条边的无向图,每条边只能走一次,要从 $1$ 号点到 $N$ 号点走 $T$ 次,问:最大边权的最小值。
我们假设答案是 $x$,那么如果只走边权属于 $[1,y_0]\ (y_0<x)$ 的边,一定不能走到,因为如果能走到的话,$x$ 会更小。如果只走边权属于 $[1,y_1]\ (y_1>x)$ 的边,一定可以走到,所以说答案具有二段性,所以我们可以通过二分来求出答案。

如果我们二分出来的值是 $m$ 的话,我们需要判断:如果只走边权属于 $[1,m]$ 的边,能不能从 $1$ 号点到 $N$ 号点走 $T$ 次,如果可以,那么就到左边二分,否则就到右边二分。
可以先把长度大于 $m$ 的边删掉,然后问题就变成了:给定一个无向图,判断是否存在 $T$ 条从 $1$ 号点到 $T$ 号点相互之间没有公共边的路径。然后我们再将这个问题转化为网络流问题。
由于每条边只能走一次,所以每条边的容量为 $1$;将 $1$ 号点当作源点,将 $N$ 号点当作汇点;对于无向图,我们可以建两条有向边;然后求最大流,流量就是有几条路径,所以只需要判断一下流量和 $T$ 的大小关系就可以了。
问题 $1$:原问题说正反两条边只能流一次,但是我们建的流网络是正反各能流一次,这两个等价吗?我们仔细想想,正着流一次,反着再流一次,就相当于没流,所以如果出现了这种情况,只需要删除两条边的流量就可以了。
问题 $2$:建立残留网络的时候,是不是要建四条边?当我们建立流网络的时候,如果两条边重合,那么就相当于容量相加的一条边,所以我们只需要建立两条容量为 $1$ 的边就可以了。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=210,M=80010,inf=0x3f3f3f3f;
int n,m,K,S,T;//原题的T变为K
int h[N],e[M],ne[M],f[M],w[M],idx;//w表示长度
int q[N],d[N],cur[N];
void add(int a,int b,int c){
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
w[idx]=c;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[t]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
bool check(int mid){
for(int i=0;i<idx;i++){
if(w[i]>mid) f[i]=0;//删掉边
else f[i]=1;
}
return (dinic()>=K);
}
int main(){
cin>>n>>m>>K;
S=1;
T=n;
mems(h,-1);
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
int l=1,r=1e6;
while(l<r){
int mid=l+r>>1;
if(check(mid)) r=mid;//mid是可行的答案
else l=mid+1;//mid是不可行的答案
}
cout<<r;
return 0;
}
```
---
[原题](https://www.acwing.com/problem/content/2189/),[洛谷原题](https://www.luogu.com.cn/problem/P2754)。
题目概述(为了方便,将 $-1$ 号点当作 $n+1$ 号点):有 $m$ 辆公交车,在 $[0,n+1]$ 这个区间内按特定顺序移动,每移动一次花费 $1$ 天,第 $p_i$ 辆公交车最多能拉 $h_{p_i}$ 人,问 $k$ 个人从 $0$ 号点到 $n+1$ 号点需要多长时间。
判断有没有解:可以用并查集判断($0$ 号点与 $n+1$ 号点是否连通)。
寻找答案:如果从 $0$ 号点到 $n+1$ 号点需要 $d$ 天的话,那么我们就建立 $d+1$ 层图,第 $0$ 天到第 $d$ 天,每一层有 $n+2$ 个点,代表 $0$ 号点到 $n+1$ 号点。源点向 $(0,0)$ 连一条容量为 $k$ 的边,每一层的第 $n+1$ 号点向汇点连一条容量为 $+\infty$ 的边,每辆公交车按路线跨一天连一条容量为 $r_i$ 的边,每个点向明天的自己连一条容量为 $+\infty$ 的边。
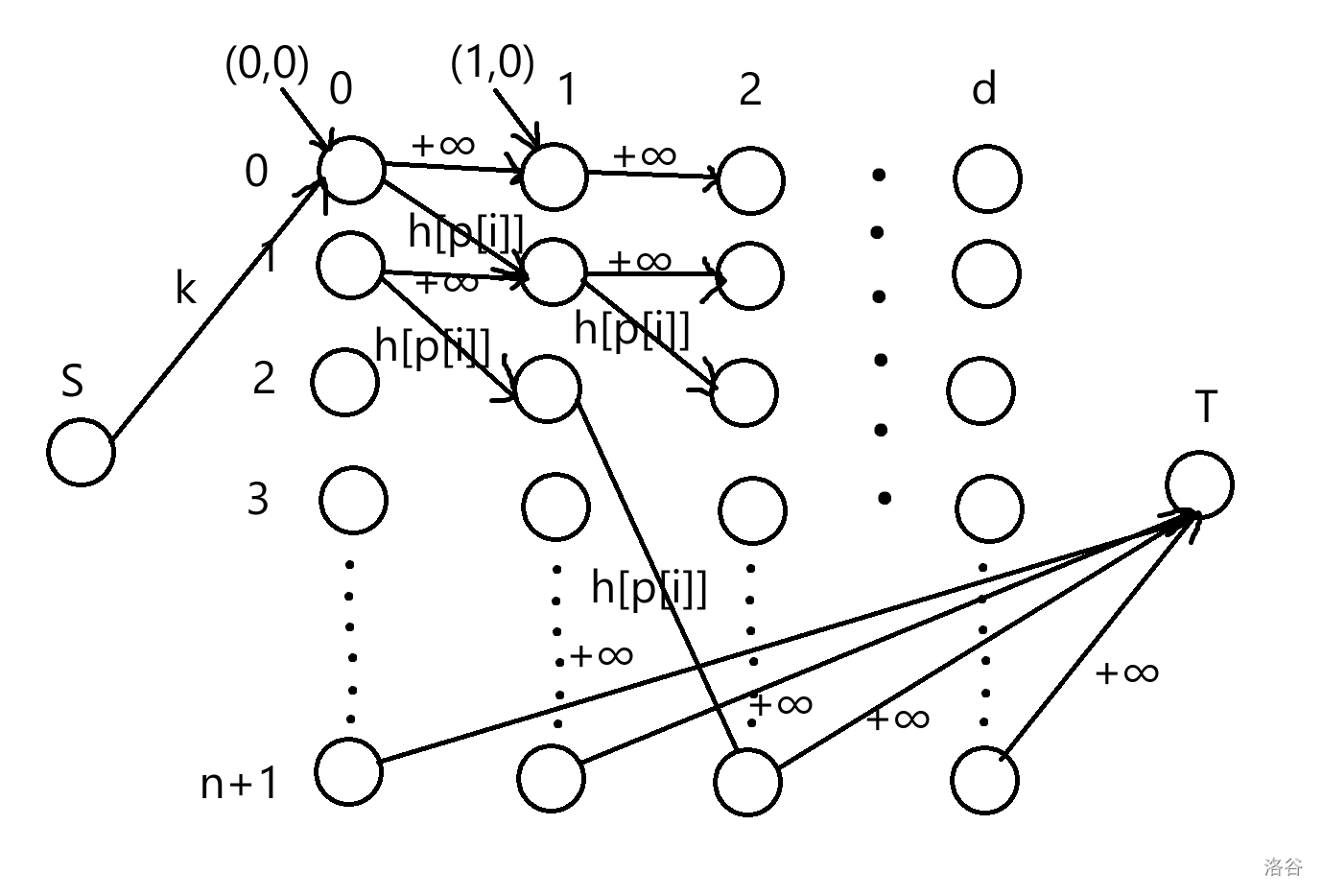
图**有点**乱,再总结一下:分为三类边,第一类是源汇连边,从源点向第 $0$ 天的第 $0$ 号点连一条容量为 $k$ 的边,从每天的第 $n+1$ 号点向汇点连一条容量为 $+\infty$ 的边;第二类是公交边,按照每辆公交的运行顺序,向明天的下一个点连一条容量为 $h_{p_i}$ 的边;第三类是等待边,因为每个站台都可以容纳无穷个人,所以每个点向明天的这个点连一条容量为 $+\infty$ 的边。
关于 $d$,因为流网络的点数是和 $d$ 成正比的,所以可以直接增加,再对剩下的增广。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=1101*22+10,M=(N+1101+13*1101)*2+10,inf=0x3f3f3f3f;
int n,m,k,S,T;
int h[N],f[M],e[M],ne[M],idx;
int q[N],d[N],cur[N];
struct ship{
int h,r,id[30];
}ships[30];
int p[30];//并查集
int find(int x){
if(p[x]!=x) p[x]=find(p[x]);
return p[x];
}
int get(int i/*空间站*/,int d/*天数*/){//获得编号
return d*(n+2)+i;
}
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[t]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
int main(){
cin>>n>>m>>k;
S=N-2;
T=N-1;
mems(h,-1);
for(int i=0;i<30;i++) p[i]=i;
for(int i=0;i<m;i++){
int a,b;
scanf("%d%d",&a,&b);
ships[i]={a,b};
for(int j=0;j<b;j++){
int id;
scanf("%d",&id);
if(id==-1) id=n+1;
ships[i].id[j]=id;
if(j>0){//合并
int x=ships[i].id[j-1];//上一个点
p[find(x)]=find(id);
}
}
}
if(find(0)!=find(n+1)) puts("0");//无解
else{
//初始的源汇边
add(S,get(0,0),k);
add(get(n+1,0),T,inf);
int day=1,ans=0;
while(1){
add(get(n+1,day),T,inf);//今天的源汇边
for(int i=0;i<=n+1;i++) add(get(i,day-1),get(i,day),inf);//等待边
for(int i=0;i<m;i++){
int r=ships[i].r;
int a=ships[i].id[(day-1)%r],b=ships[i].id[day%r];
add(get(a,day-1),get(b,day),ships[i].h);//公交边
}
ans+=dinic();//增广新加的
if(ans>=k) break;
day++;
}
cout<<day;
}
return 0;
}
```
## 拆点
[原题](https://www.acwing.com/problem/content/2242/),[洛谷原题](https://www.luogu.com.cn/problem/P2891)。
人话:三分图匹配。

我们很容易想到这样做:源点向每个食品连一条容量为 $1$ 的边,每个饮料向汇点连一条容量为 $1$ 的边,匹配的再连一条容量为 $1$ 的边。但是这样做是不对的,比如一头牛同时匹配了两种食品和三种饮料,那么它就会吃掉两份餐。
所以我们可以把每头奶牛拆成两个点,两点之间连一条容量为 $1$ 的边,这样就可以确保每头奶牛只吃一份餐了。
拆点通常会拆成两个点:入点和出点,所有连向原来点的边连向入点,所有从原来点出去的边从出点出去。所以只需要把每头牛拆成出入两点,左连入点,出点连右。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=410,M=40610,inf=0x3f3f3f3f;
int n,F,D,S,T;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
int main(){
cin>>n>>F>>D;
S=0;
T=n*2+F+D+1;
mems(h,-1);
for(int i=1;i<=F;i++) add(S,n*2+i,1);//源点
for(int i=1;i<=D;i++) add(n*2+F+i,T,1);//汇点
for(int i=1;i<=n;i++){
add(i,n+i,1);
int a,b,t;
scanf("%d%d",&a,&b);
while(a--){
scanf("%d",&t);
add(n*2+t,i,1);//食物
}
while(b--){
scanf("%d",&t);
add(i+n,n*2+F+t,1);//饮料
}
}
cout<<dinic();
return 0;
}
```
---
[原题](https://www.acwing.com/problem/content/2182/),[洛谷原题](https://www.luogu.com.cn/problem/P2766)。
第一问:直接 DP。
第二问:枚举 DP 数组的每一个元素,对于每一个元素再遍历一遍数组,如果 $g(i)=g(j)+1$ 的话,从 $j$ 向 $i$ 连一条容量为 $1$ 的边,因为每个点只能选一次,所以拆点,中间连一条容量为 $1$ 的边。源点向每个 $g(i)=1$ 的点连边,所有 $g(i)=s$ 的点向汇点连边。
第三问:(对于第 $1$ 个点和第 $n$ 个点)将入点连向出点的边的容量设为 $+\infty$,源点和汇点的连边容量也设为 $+\infty$。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=1010,M=251010,inf=0x3f3f3f3f;
int n,S,T;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];
int g[N],w[N];
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
int main(){
cin>>n;
S=0;
T=n*2+1;
mems(h,-1);
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
int s=0;
for(int i=1;i<=n;i++){
add(i,i+n,1);
g[i]=1;
for(int j=1;j<i;j++)
if(w[j]<=w[i]) g[i]=max(g[i],g[j]+1);
for(int j=1;j<i;j++)
if(w[j]<=w[i] && g[j]+1==g[i]) add(n+j,i,1);
s=max(s,g[i]);
if(g[i]==1) add(S,i,1);
}
for(int i=1;i<=n;i++)
if(g[i]==s) add(n+i,T,1);
cout<<s<<endl;
if(s==1){//因为如果s==1的话,从S到T的流量在第三问中将不受限制,所以需要特判
cout<<n<<endl<<n;
return 0;
}
int ans=dinic();
cout<<ans<<endl;
for(int i=0;i<idx;i+=2){
int a=e[i^1],b=e[i];
if(a==S && b==1) f[i]=inf;
else if(a==1 && b==n+1) f[i]=inf;
else if(a==n && b==n+n) f[i]=inf;
else if(a==n+n && b==T) f[i]=inf;
}
cout<<ans+dinic();
return 0;
}
```
---
[原题](https://www.acwing.com/problem/content/2280/),[转存](https://www.luogu.com.cn/paste/88h1x3aq)。
我们可以把企鹅看成流,然后源点向每个有企鹅的冰块连边,因为我们要求的是汇点,所以枚举汇点。如果两个冰块之间能相互到达,那么就相互连一条容量为 $+\infty$ 的边。对于冰块起跳限制,我们可以将每个冰块拆成两个点,两个点之间连一条容量为 $m_i$ 的边。最后只需要判断最大流的流量是不是企鹅的数量就可以了。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
#define PII pair<int,int>
#define x first
#define y second
using namespace std;
const int N=210,M=20410,inf=0x3f3f3f3f;
const double eps=1e-8;
int n,S,T;
double D;
int h[N],e[M],ne[M],f[M],idx;
int d[N],q[N],cur[N];
PII p[N];//坐标
bool check(PII a,PII b){
int dx=a.x-b.x,dy=a.y-b.y;
return (sqrt(dx*dx+dy*dy)<D+eps);
}
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
int main(){
int cases;
cin>>cases;
while(cases--){
mems(h,-1);
idx=0;
scanf("%d%lf",&n,&D);
S=0;
int tot=0;//总人数
for(int i=1;i<=n;i++){
int x,y,a,b;
scanf("%d%d%d%d",&x,&y,&a,&b);
p[i]={x,y};
add(S,i,a);
add(i,i+n,b);
tot+=a;
}
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
if(check(p[i],p[j])){//可以跳
add(i+n,j,inf);
add(j+n,i,inf);
}
int cnt=0;
for(int i=1;i<=n;i++){
T=i;
for(int j=0;j<idx;j+=2){//还原网络
f[j]+=f[j^1];
f[j^1]=0;
}
if(dinic()==tot){
printf("%d ",i-1);
cnt++;
}
}
if(cnt==0) puts("-1");
else puts("");
}
return 0;
}
```
## 建图
[原题](https://www.acwing.com/problem/content/2239/),[转存](https://www.luogu.com.cn/paste/mmawqj4s)。
我们先考虑没有第二条的情况,那么这道题就是一个简单的二分图匹配问题,如果加上第二条,也就是每个猪舍之间的转移,可以从顾客向每个猪舍连一条容量为 $+\infty$ 的边,相当于通过顾客来转移猪。但是这样做会打乱时序,换句话说,所有顾客在同一时间来买猪,所以我们可以删掉猪舍对应的点,直接从先来的顾客向后来的顾客连边。

对于顾客匹配的猪舍,如果猪舍是第一次被打开的话,就从源点向顾客连一条容量为初始猪数量的边,如果不是第一次被打开,可以从上一个打开的顾客向这个顾客连一条容量为 $+\infty$ 的边,每个顾客向汇点连一条容量为自己购买数量的边。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=110,M=200020,inf=0x3f3f3f3f;
int n,m,S,T;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];
int w[1010],last[1010];//猪舍猪的数量和上一次打开这个猪舍的人
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
int main(){
cin>>m>>n;
S=0;
T=n+1;
mems(h,-1);
for(int i=1;i<=m;i++) scanf("%d",&w[i]);
for(int i=1;i<=n;i++){
int a,b;
scanf("%d",&a);
while(a--){
int id;
scanf("%d",&id);
if(!last[id]) add(S,i,w[id]);
else add(last[id],i,inf);
last[id]=i;//更新上一次打开猪舍的人
}
scanf("%d",&b);
add(i,T,b);
}
cout<<dinic();
return 0;
}
```
# 最小割
## 算法模板
通过最大流最小割定理得知,如果 $f$ 为最大流,那么一定存在一个割使得 $|f|=c(S,T)$,又因为最小割一定小于所有割,所以 $|f|=c(S,T)\ge$ 最小割。
又通过割的性质得知,最大流 $\le$ 最小割,综合得到最大流等于最小割,那么我们只需要再写一遍最大流的代码就可以了。
## 直接应用
[原题](https://www.acwing.com/problem/content/2281/),[转存](https://www.luogu.com.cn/paste/0q8tbefc)。
对于这种形式,我们可以随便找一个数 $\lambda$,如果 $\displaystyle \frac{\sum w_e}{|C|}<\lambda$,那么
$$
\Leftrightarrow \sum w_e<|C|\lambda\\
\Leftrightarrow \sum w_e-|C|\lambda<0\\
\Leftrightarrow \sum(w_e-\lambda)<0
$$
对于最后的变形,因为 $\sum w_e$ 中一共有 $|C|$ 个元素,所以就提取了一下。
如果 $\displaystyle \frac{\sum w_e}{|C|}>\lambda$ 的话,同理。那么给出 $\lambda$ 后,只需要判断 $\sum(w_e-\lambda)$ 的最小值是不是大于 $0$,如果 $\sum(w_e-\lambda)>0$,那么就说明 $\displaystyle \frac{\sum w_e}{|C|}>\lambda$,所以说我们要求的最小值要比 $\lambda$ 大,反之同理,$\lambda$ 只需要二分就可以了。可以推出想让 $\displaystyle \frac{\sum w_e}{|C|}$ 最小就相当于要让 $\sum w_e$ 最小。
这个式子的值只需要把原图 $G$ 的每条边的值减去 $\lambda$ 得到一个新图 $G'$,那么
- $w_e'<0$,则必选。
- 对于剩下的边,我们先按下面的方式划分集合,因为我们要选尽量少的边,所以我们不应该选两个集合中的边,之选集合之间的边,那么只需要求最小割就可以了。
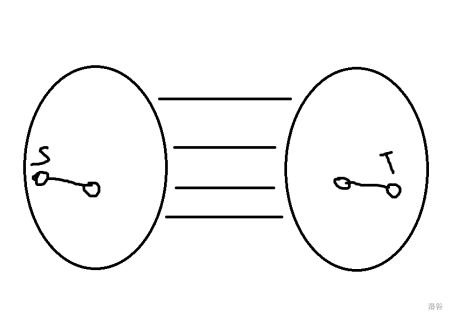
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=110,M=810,inf=0x3f3f3f3f;
const double eps=1e-8;
int n,m,S,T;
int h[N],e[M],ne[M],w[M],idx;
double f[M];
int q[N],d[N],cur[N];
void add(int a,int b,int c){
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
w[idx]=c;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
double find(int u,double limit){
if(u==T) return limit;
double flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
double t=find(ver,min(f[i],limit-flow));
if(t<eps) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
double dinic(double mid){
double ans=0;
for(int i=0;i<idx;i+=2){
if(w[i]<=mid){//必选
ans+=w[i]-mid;
f[i]=f[i^1]=0;
}
else f[i]=f[i^1]=w[i]-mid;
}
double r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r+ans;
}
int main(){
cin>>n>>m>>S>>T;
mems(h,-1);
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c);
}
double l=0,r=1e7;
while(r-l>eps){
double mid=(l+r)/2;
if(dinic(mid)<0) r=mid;
else l=mid;
}
printf("%.2lf",r);
return 0;
}
```
---
[原题](https://www.acwing.com/problem/content/2282/),[转存](https://www.luogu.com.cn/paste/uyfm8j7w)。
在异或运算中,每一位的运算都是独立的,所以我们希望最后的结果最小,就是让每一位最小。设当前看的是第 $k$ 位,那么所有点只会被分为两类:第 $k$ 位为 $0$ 的和第 $k$ 位为 $1$ 的,则如果两个点都是第一类,异或后还是 $0$,如果都是第二类,异或后仍然是 $0$,如果两个点不同类,异或后就是 $1$,如果有 $m$ 个不同类的,那么第 $k$ 为贡献的答案就是 $m\cdot 2^k$,我们希望答案尽可能小,就可以让 $m$ 尽可能小,就相当于让不同类的点尽可能少,现在就可以转化成最小割问题了。
对于原先有编号,如果属于第一类,就从源点向这个点连一条容量为 $+\infty$ 的边,如果属于第二类,就向汇点连一条容量为 $+\infty$ 的边,其余边的容量都设为 $1$。
做完最小割后,我们可以在残留网络中从源点出发,沿着容量大于 $0$ 的边搜索,如果能搜到,就是第一类,搜不到就是第二类。
参考代码:
```cpp
#include<bits/stdc++.h>
#define LL long long
#define mems(a,b) memset(a,b,sizeof a)
#define PII pair<int,int>
#define x first
#define y second
using namespace std;
const int N=510,M=(3000+N*2)*2,inf=0x3f3f3f3f;
int n,m,k,S,T;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];
int p[N];
PII edges[3010];//存图
void add(int a,int b,int c,int d){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=d;
ne[idx]=h[b];
h[b]=idx++;
}
void build(int k){//建图
mems(h,-1);
idx=0;
for(int i=1;i<=m;i++){
int a=edges[i].x,b=edges[i].y;
add(a,b,1,1);
}
for(int i=1;i<=n;i++)
if(p[i]>=0){
if(p[i]>>k&1) add(i,T,inf,0);
else add(S,i,inf,0);
}
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
LL dinic(int k){
build(k);
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
int main(){
cin>>n>>m;
S=0;
T=n+1;
for(int i=1;i<=m;i++) scanf("%d%d",&edges[i].x,&edges[i].y);
cin>>k;
mems(p,-1);
while(k--){
int a,b;
scanf("%d%d",&a,&b);
p[a]=b;
}
LL ans=0;
for(int i=0;i<=30;i++) ans+=dinic(i)<<i;//可能越界
cout<<ans;
return 0;
}
```
## 最大权闭合图
[原题](https://www.acwing.com/problem/content/963/),[洛谷原题](https://www.luogu.com.cn/problem/P4174)。
一个点集,要求其中的点不能指向点集外的点,这个点集加上点集中的边,就是闭合(子)图,最大权闭合图就是指这个图的所有闭合图中权值和最大的那个,其中的权值会在点上。
我们先把这个有向图 $G=(V,E)$ 转化为一个流网络 $N=(V_N,E_N)$,如果这个点的点权为正,那么就从源点向这个点连一条容量为这个点点权的边;如果点权为负,那么就从这个点向汇点连一条容量为这个点点权的绝对值的边;如果点权为 $0$,就不用连边;其余边的容量设为 $+\infty$。
所以 $V_N=V+\{s,t\},E_N=\{(s,u)|w_u>0\}\cup\{(u,t)|w_u<0\}\cup E$。
针对这个问题,我们定义一种割,称为简单割,就是说割边一定与源点或汇点相连的割。不难发现,上面的流网络的最小割就是一个简单割,因为最大流 $=$ 最小割,而最大流一定是有限的,所以最小割也一定是有限的,那么割边就不能是容量为 $+\infty$ 的边,也就是中间不与源点和汇点相连的边。
我们将闭合子图的点集设为 $V'$,割 $[S,T]$ 可以这样分割:$S=V'+{s},T=V_N-S$,因为从 $V'$ 中的任何一个点走,只能走到 $V'$ 中的点,所以如果割边在中间的话,$S$ 和 $T$ 间就没有边相连,那么割边就只能与源点或汇点相连,很显然,这些割都是简单割。
如果 $[S,T]$ 是一个简单割,定义 $V'=S-\{s\}$,那么就不存在一条原图中的边,使得 $S$ 中的点能走到 $T$,也就是说,$S$ 中的点只能走到 $S$,所以 $V'$ 就是闭合图。
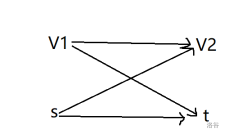
根据上面的推到得知,闭合图 $\hArr$ 简单割。我们现在已知一个简单割 $[S,T]$,设 $V_1=S-\{s\},V_2=V-V_1$,现在将这个割的容量 $c[S,T]$ 拆分开,可以得到上面的四对,因为这是一个简单割,所以不存在从 $V_1$ 到 $V_2$ 的边,显然这个流网络中是不存在 $s$ 到 $t$ 的边,下面我们用 $V_1^+$ 来表示 $V_1$ 中点权为正的点,$V_1^-$ 来表示 $V_1$ 中点权为负的点,那么
$$
c[S,T]\\
=c[V_1,\{t\}]+c[\{s\},V_2]\\
=\sum_{v\in V_2^+} w_v+\sum_{v\in V_1^-} (-w_v)\\
w(V_1)\\
=\sum_{v\in V_1^+} w_v+\sum_{v\in V_1^-} w_v\\
=\sum_{v\in V_1^+} w_v-\sum_{v\in V_1^-} (-w_v)
$$
两者相加可得
$$
c[S,T]+w(V_1)\\
=\sum_{v\in V_2^+} w_v+\sum_{v\in V_1^+} w_v\\
=\sum_{v\in V^+} w_v\\
=w(V^+)
$$
因为 $w(V^+)$ 是一个定值,所以说如果我们希望 $w(V_1)$ 最大,就是要让 $c[S,T]$ 最小,那么答案就是总正权值 $-$ 最小割。
回到题目,概括题意:一共有 $n$ 个地点可以建立通讯站,在每个地点建立通讯站的花费是不同的,在第 $i$ 个地点建立通讯站需要花费 $p_i$ 元。有 $m$ 个用户群,满足每个用户群需要建立他们需要的两个通讯站,如果满足了一个用户群,就会获得 $c_i$ 的收益,问如何建立通讯站,使得总收益最大。
我们可以将每个通讯站看成一个点,点权为 $-p_i$,每个用户群也看成一个点,点权为 $c_i$,每个用户群向需要的两个通讯站连边,那么要选一个用户群就需要选两个相连的通讯站,也就是要选闭合图,现在希望权值最大,所以这就是最大权闭合图问题。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=55010,M=(50000*3+5000)*2+10,inf=0x3f3f3f3f;
int n,m,S,T;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
int main(){
cin>>n>>m;
S=0;
T=n+m+1;
mems(h,-1);
for(int i=1;i<=n;i++){
int p;
scanf("%d",&p);
add(m+i,T,p);
}
int tot=0;
for(int i=1;i<=m;i++){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(S,i,c);
add(i,m+a,inf);
add(i,m+b,inf);
tot+=c;
}
cout<<tot-dinic();
return 0;
}
```
## 最大密度子图
[原题](https://www.acwing.com/problem/content/2326/),[洛谷原题](https://www.luogu.com.cn/problem/UVA1389)。
定义:在原图 $G=(V,E)$ 中选一个点集 $V'$ 和一个边集 $E'$,使得 $E'$ 内任何一条边相连接的两个点都在 $V'$ 中,且使 $\displaystyle \frac{|E'|}{|V'|}$ 最大(让选出的子图最稠密)。
最大化分式的值,可以用前面讲过的 **01 分数规划**解决,每次二分一个值 $g$,若 $max(|E'|-g\cdot |V'|)>0$,就等价于 $\displaystyle \frac{|E'|}{|V'|}>g$,然后根据结果二分。
很显然,如果点集已经固定,那么将点集内的边全部选上,就是最优解。
我们现在考虑如何求 $max(|E'|-g|V'|)$,通过简单的变换可得,如果要让 $|E'|-g|V'|$ 最大,就相当于让 $g|V'|-|E'|$ 最小,现在设 $d_v$ 为 $v$ 这个点的度数,那么($\overline{V'}$ 是 $V'$ 的补集)
$$
g\cdot |V'|-|E'|\\
=\sum_{v\in V'} g-\displaystyle \frac{\sum_{v\in V'} d_v-c[V',\overline{V'}]}{2}\\
=\sum_{v\in V'} (g-\frac{d_v}{2})+\frac{c[V',\overline{V'}]}{2}\\
=\frac{1}{2}(\sum_{v\in V'} (2g-d_v)+c[V',\overline{V'}])
$$
我们发现 $\sum_{v\in V'}(2g-d_v)$ 非常~~烦人~~,所以我们考虑合理构建图,以将这一项合并到最小割。将 $d_v$ 看成点权,那么可以让原图中的所有点向汇点连一条容量为 $2g-d_v$ 的边,让原图的边的容量设为 $1$,源点向原图中的所有点连一条容量为 $U$,考虑到 $2g-d_v$ 可能为负数,所以将所有连向汇点的边也加上 $U$,我们只要保证 $U$ 比所有的度数大就可以了,所以 $U$ 可以直接取 $m$。
现在设 $c[S,T]$ 为流网络的其中一个割,定义 $V=新图整个点集-\{s,t\},V'=S-\{s\},\overline{V'}=V-V'$,按之前的拆分方法可以得到下面的四种组合,显然不存在 $s$ 到 $t$ 的边,所以我们整理剩下的三种组合:
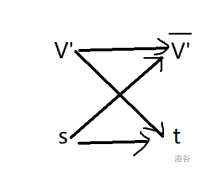
现在设 $E'$ 为 $V'$ 中两两相连的边,整理 $c[S,T]$ 得
$$
c[S,T]\\
=\sum_{v\in \overline{V'}} U+\sum_{u\in V'}(U+2g-d_u)+\sum_{u\in V'}\sum_{v\in \overline{V'}}c_{u,v}\ \ \ \ \ \ \ \ \ 1\\
=\sum_{v\in \overline{V'}} U+\sum_{u\in V'}(U+2g-d_u+\sum_{v\in \overline{V'}}c_{u,v})\\
=\sum_{v\in \overline{V'}} U+\sum_{u\in V'}(U+2g-(d_u-\sum_{v\in \overline{V'}}c_{u,v}))\\
=\sum_{v\in \overline{V'}} U+\sum_{u\in V'}(U+2g-\sum_{v\in V'}c_{u,v})\ \ \ \ \ \ \ \ \ \ \ 2\\
=\sum_{v\in V} U+\sum_{u\in V'} 2g-\sum_{u\in V'}\sum_{v\in V'} c_{u,v}\\
=U\cdot n+\sum_{u\in V'} 2g-\sum_{u\in V'}\sum_{v\in V'} c_{u,v}\\
=U\cdot n+|V'|\cdot 2g-2\cdot |E'|\ \ \ \ \ \ \ \ \ \ \ 3\\
=U\cdot n+2(g\cdot |V'|-|E'|)
$$
解析:[$1$](https://www.luogu.com.cn/paste/smlkiyla),[$2$](https://www.luogu.com.cn/paste/572mrusa),[$3$](https://www.luogu.com.cn/paste/bk0ehl3o)。
我们希望 $g\cdot |V'|-|E'|$ 最小,因为 $U\cdot n$ 为定值,所以就等价于让 $c[S,T]$ 最小,也就是要求最小割,整理答案得 $ans=\displaystyle \frac{U\cdot n-c[S,T]}{2}$。
这题要求我们输出方案,在上面的证明中我们知道,$V'$ 就是一个合法方案,所以我们可以在残留网络中沿着容量大于 $0$ 的边走,能走到的点就是 $S$ 中的点,然后将 $s$ 点删掉就是 $V'$。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=110,M=(1000+N*2)*2,inf=0x3f3f3f3f;
const double eps=1e-8;
int n,m,S,T;
int h[N],e[M],ne[M],idx;
double f[M];
int q[N],d[N],cur[N];
int dg[N];//度数
struct node{//存图
int a,b;
}edge[M];
int ans;
bool st[N];
void add(int a,int b,double c,double d){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=d;
ne[idx]=h[b];
h[b]=idx++;
}
void build(double g){//建图
mems(h,-1);
idx=0;
for(int i=1;i<=m;i++) add(edge[i].a,edge[i].b,1,1);
for(int i=1;i<=n;i++){
add(S,i,m,0);
add(i,T,m+2*g-dg[i],0);
}
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
double find(int u,double limit){
if(u==T) return limit;
double flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
double t=find(ver,min(f[i],limit-flow));
if(t<=0) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
double dinic(double g){
build(g);
double r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
void dfs(int u){
st[u]=true;
if(u!=S) ans++;
for(int i=h[u];~i;i=ne[i]){
int ver=e[i];
if(!st[ver] && f[i]>0) dfs(ver);
}
}
int main(){
cin>>n>>m;
S=0;
T=n+1;
for(int i=1;i<=m;i++){
int a,b;
scanf("%d%d",&a,&b);
dg[a]++;
dg[b]++;
edge[i]={a,b};
}
double l=0,r=m;
while(r-l>eps){
double mid=(l+r)/2;
double t=dinic(mid);
if(m*n-t>0) l=mid;
else r=mid;
}
dinic(l);
dfs(S);
if(ans==0){
cout<<1<<endl<<1;
return 0;
}
cout<<ans<<endl;
for(int i=1;i<=n;i++)
if(st[i]) printf("%d\n",i);
return 0;
}
```
## 最小权点覆盖集
[原题](https://www.acwing.com/problem/content/2327/),[转存](https://www.luogu.com.cn/paste/505tf4yo)。
点覆盖集:在一个无向图中,选一个点集,使得每一条边连接的点中至少有一个点在这个点集内,最小权就是让选出来的点的权值和最小。
在一般的图中,这个问题是一种 NPC 问题(只能暴搜得到答案),所以说我们这里只研究**二分图**的最小权点覆盖集。
因为二分图最大匹配中的边两两没有公共点,所以说最大匹配数 $=$ 最小点覆盖数,如果点权不为 $1$ 的话,就只能用网络流来解决。
我们可以让中间的边的容量设为 $+\infty$,这样就能保证中间不存在割边,换而言之,割边只能出现在左边或右边;源点向左边的点连一条容量为它的点权的边,右边的点向汇点连一条容量为点权的边。
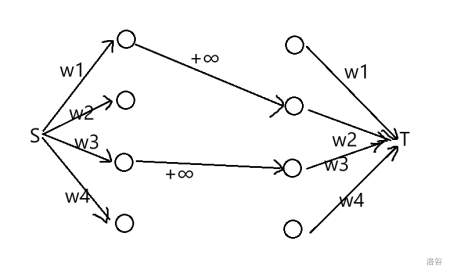
很显然,这个流网络的最小割与最小权点覆盖集是一一对应的。
回到题目,现在将 $a^-$ 定义为删除从 $a$ 出发的边的花费,将 $b^+$ 定义为删除到达 $b$ 的边的花费,我们发现如果要删除 $a$ 到 $b$ 的边,要么操作 $a^-$,要么操作 $b^+$,注意到这和我们之前的问题有点相似,所以我们可以按下面的步骤转化。
因为每个点都有两种操作,所以我们将每个点进行拆点,左边为入点($+$ 的点),右边为出点($-$ 的点),如果这条边是 $a$ 到 $b$ 的边,就从左边的 $b$ 向右边的 $a$ 连一条边,这样就可以构造出一个二分图,且能转化成最小权点覆盖集问题。
我们先考虑如何输出方案,首先将最大流对应到最小割的方案:在残留网络中,从 $s$ 出发,沿着容量大于 $0$ 的边,能走到的点就是集合 $S$ 中的点,剩下的就是集合 $T$ 中的点;现在找出所有的割边,如果割边是左边的边,就说明选的是 $+$ 的点,否则就是选了 $-$ 的点。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=210,M=5200*2+10,inf=0x3f3f3f3f;
int n,m,S,T;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];
bool st[N];
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
void dfs(int u){
st[u]=true;
for(int i=h[u];~i;i=ne[i])
if(f[i] && !st[e[i]]) dfs(e[i]);
}
int main(){
cin>>n>>m;
S=0;
T=n*2+1;
mems(h,-1);
for(int i=1;i<=n;i++){
int w;
scanf("%d",&w);
add(S,i,w);
}
for(int i=1;i<=n;i++){
int w;
scanf("%d",&w);
add(i+n,T,w);
}
while(m--){
int a,b;
scanf("%d%d",&a,&b);
add(b,n+a,inf);
}
cout<<dinic()<<endl;
dfs(S);
int cnt=0;
for(int i=0;i<idx;i+=2){
int a=e[i^1],b=e[i];
if(st[a] && !st[b]) cnt++;//a属于S且b属于T
}
cout<<cnt<<endl;
for(int i=0;i<idx;i+=2){
int a=e[i^1],b=e[i];
if(st[a] && !st[b])
if(a==S) printf("%d +\n",b);
}
for(int i=0;i<idx;i+=2){
int a=e[i^1],b=e[i];
if(st[a] && !st[b])
if(b==T) printf("%d -\n",a-n);
}
return 0;
}
```
## 最大权独立集
[原题](https://www.acwing.com/problem/content/2328/),[洛谷原题](https://www.luogu.com.cn/problem/P4474)。
定义:选出总权值和最大的点集,使得点集中的点两两之间没有边。
在所有点权都等于 $1$ 时,求最大独立集 $\Leftrightarrow$ 去掉最少的点,使得所有边都破坏掉 $\Leftrightarrow$ 去掉最小点覆盖,所以最大独立集 $=n-$ 最小点覆盖。
如果带上点权,那么显然最大权独立集 $=$ 总权值 $-$ 最小权点覆盖集。
观察题目,我们发现下面几个性质:
- 只能在偶数秒拿走宝石。
- 不可能同时拿走相邻格子上的宝石。
现在我们将格子看成点,相邻两个格子连边,那么我们选出的点集一定是一个最大权独立集;又因为这是一个网格图,所以可以将这个图进行染色,那么所有的边一定连接一个红色的点和一个黄色的点,如果将红色格子放到一边,黄色格子放到一边,不难发现,这就是一个二分图。很显然,原问题现在被转化成最大权独立集问题。
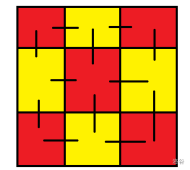
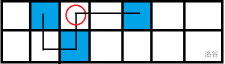
现在问题来了:如何将一个独立集转化成合法方案?我们可以两行两行走,如果下一个格子的下一个格子是目标宝石,就判断下一步是奇数秒还是偶数秒,如果是奇数秒,直接走,如果是偶数秒,就停一下再走。可以参考下面的图片,蓝色代表目标宝石,红色圈代表在这个格子停一秒,黑色的线代表路线。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=10010,M=60010,inf=0x3f3f3f3f;
int n,m,S,T;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];
int get(int x,int y){
return (x-1)*m+y;
}
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
int main(){
cin>>n>>m;
mems(h,-1);
S=0;
T=n*m+1;
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
int tot=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
int w;
scanf("%d",&w);
if(i+j&1){//i+j为奇数
add(S,get(i,j),w);
for(int k=0;k<4;k++){
int x=i+dx[k],y=j+dy[k];
if(x>=1 && x<=n && y>=1 && y<=m) add(get(i,j),get(x,y),inf);
}
}
else add(get(i,j),T,w);//因为这里设左边为奇数点,而最小割只算正向边,所以这里不需要再向四周连边
tot+=w;
}
cout<<tot-dinic();
return 0;
}
```
## 建图
[原题](https://www.acwing.com/problem/content/description/383/),[洛谷原题](https://www.luogu.com.cn/problem/UVA1660),[~~双倍经验~~](https://www.luogu.com.cn/problem/SP300)。
枚举 $s,t$,原问题转化成删掉一些点,使得源点和汇点不连通,但是我们最小割割的是边,不是点,所以可以拆点,两个点之间相互连一条容量为 $1$ 的边,原图中边的容量设为 $+\infty$。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=110,M=5200,inf=0x3f3f3f3f;
int n,m,S,T;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
int main(){
while(cin>>n>>m){
mems(h,-1);
idx=0;
for(int i=0;i<n;i++){
add(i,n+i,1);
add(n+i,i,1);
}
while(m--){
int a,b;
scanf(" (%d,%d)",&a,&b);
add(a+n,b,inf);
add(b+n,a,inf);
}
int ans=inf;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++){
S=i+n;
T=j;
for(int k=0;k<idx;k+=2){//还原流网络
f[k]+=f[k^1];//反向边的流量流回正向边
f[k^1]=0;//清空反向边
}
ans=min(ans,dinic());
}
if(ans==inf) ans=n;
printf("%d\n",ans);
}
return 0;
}
```
---
[原题](https://www.acwing.com/problem/content/2178/),[转存](https://www.luogu.com.cn/problem/P2762)。
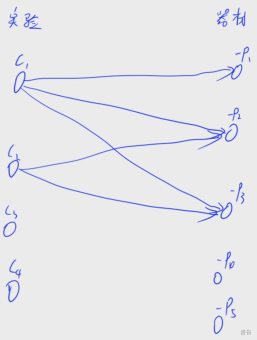
要求沿着与它相连的任何一条边走,走到的点都在这个点集里,不难看出,这就是一个最大权闭合图问题的板子。
输出方案:从 $s$ 出发,能遍历到的点就属于 $S$,否则属于 $T$,在 $S$ 中的点就是我们选出的点。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=110,M=5210,inf=0x3f3f3f3f;
int n,m,S,T;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];
bool st[N];
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
q[0]=S;
d[S]=0;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
void dfs(int u){
st[u]=true;
for(int i=h[u];~i;i=ne[i])
if(f[i]>0 && !st[e[i]]) dfs(e[i]);
}
int main(){
cin>>m>>n;
S=0;
T=m+n+1;
mems(h,-1);
getchar();//过滤回车
int tot=0;
for(int i=1;i<=m;i++){
int w,id;
string line;
getline(cin,line);//读入整行
stringstream ssin(line);//字符串转换成数字,并根据空格记录在一个“数组”中
ssin>>w;
add(S,i,w);
while(ssin>>id) add(i,m+id,inf);
tot+=w;
}
for(int i=1;i<=n;i++){
int p;
scanf("%d",&p);
add(m+i,T,p);
}
int ans=dinic();
dfs(S);
for(int i=1;i<=m;i++)
if(st[i]) printf("%d ",i);
puts("");
for(int i=m+1;i<=m+n;i++)
if(st[i]) printf("%d ",i-m);
puts("");
cout<<tot-ans;
return 0;
}
```
---
[原题](https://www.acwing.com/problem/content/2200/),[洛谷原题](https://www.luogu.com.cn/problem/P3355)。
我们将所有能够互相攻击到的点连边,原问题转化成:选出一些点,使得选出的点之间不存在边,AUV,这不就是最大独立集吗?
同时,这题也是一个二分图,原问题的配图已经疯狂暗示了,而且每条边连的点一定是一个$\color{red}红点$和一个$\color{#DADA00}黄点$。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=40010,M=400010,inf=0x3f3f3f3f;
int n,m,S,T;
int h[N],e[M],ne[M],f[M],idx;
int q[N],d[N],cur[N];
bool g[210][210];
int get(int x,int y){
return (x-1)*n+y;
}
void add(int a,int b,int c){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
h[b]=idx++;
}
bool bfs(){
int hh=0,tt=0;
mems(d,-1);
d[S]=0;
q[0]=S;
cur[S]=h[S];
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1 && f[i]>0){
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T) return true;
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i && flow<limit;i=ne[i]){
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1 && f[i]>0){
int t=find(ver,min(f[i],limit-flow));
if(t==0) d[ver]=-1;
f[i]-=t;
f[i^1]+=t;
flow+=t;
}
}
return flow;
}
int dinic(){
int r=0,flow;
while(bfs())
while(flow=find(S,inf)) r+=flow;
return r;
}
int main(){
cin>>n>>m;
S=0;
T=n*n+1;
mems(h,-1);
while(m--){
int x,y;
scanf("%d%d",&x,&y);
g[x][y]=true;
}
int dx[8]={-2,-1,1,2,2,1,-1,-2};
int dy[8]={1,2,2,1,-1,-2,-2,-1};
int tot=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
if(g[i][j]) continue;
if(i+j&1){
add(S,get(i,j),1);
for(int k=0;k<8;k++){
int x=dx[k]+i,y=dy[k]+j;
if(x>=1 && x<=n && y>=1 && y<=n && !g[x][y]) add(get(i,j),get(x,y),inf);
}
}
else add(get(i,j),T,1);
tot++;
}
cout<<tot-dinic();
return 0;
}
```
## 平面图转最短路
### 一些定义
平面嵌入:在平面上可画出的无交叉边的图(可以有曲线)。
可平面图:能转化成平面嵌入发图。
平面图:可平面图的任意一个平面嵌入。
平面图的面:每一个闭合的区域(整个外界也算一个面)。
平面图的边界:一个面的边界。
对偶图:对于一个平面图 $G$,按下面的步骤建出来的图就是原图的对偶图:
1. 在 $G$ 中每一个面 $r_i$ 设一个结点 $v_i$。
2. 过 $r_i$ 和 $r_j$ 的公共边界 $e_k$ 做一条边 $(v_i,v_j)$ 与 $e_k$ 相交。
3. 当 $e_k$ 只为 $r_i$ 的边界时,在 $v_i$ 上作一个环与 $e_k$ 相交(即割边需要做一个环)。
### 算法
当原网络 $G$ 是平面图,那么把容量转化为边权后,再转化成对偶图 $G'$,那么 $G$ 的最小割(最大流)就是 $G'$ 的最短路。这样就可以降低时间复杂度。
暂时没有找到合适的题目。
# 费用流
## 含义
题目会给每条边赋予一个边权 $w(u,v)$,而费用流指所有最大可行流中,费用的最小(大)值。
一个可行流的费用定义为 $\sum f(u,v)\cdot w(u,v)$。
## 算法模板
[原题](https://www.acwing.com/problem/content/2176/),[洛谷原题](https://www.luogu.com.cn/problem/P3381)。
直接将 EK 算法中的 bfs 函数换成 SPFA 即可。
~~智障~~证明(设 $c(p)$ 为路径 $p$ 的长度):
假设可行流 $f$ 是一个最小费用流,流量为 $v$,且残留网络 $G_f$ 中无负环,现在按最短路径 $p$ 增广,得到新流 $f'$,流量为 $v+\delta$,则 $\operatorname{cost}(f'-f)=c(p)\delta$。假设存在一个可行流 $f_n$,使得 $|f_n|=v+\delta$,且 $f_n$ 的费用小于 $f'$ 的费用,考虑流差 $f_n-f$,因为流的分解定理,$f_n-f$ 可以分解为若干从源到汇的路径和若干环:
- 路径:**至少存在一条路径 $p'$,使得 $p'$ 的长度小于 $p$ 的长度,否则 $f_n$ 的费用不可能小于 $f$ 的费用。**
- 环:由于 $G_f$ 中不存在负环,所以环贡献的长度和费用一定非负,为了降低费用,一定不选环。
因为 $p$ 为最短路径,所以不存在 $p'$ 的长度小于 $p$ 的长度,所以不存在 $p'$,那么 $f'$ 就是最优解。
现在证明加黑部分:
设 $f_n-f$ 分解出来的路径分别为 $p_1,p_2,...,p_k$,每条路径 $p_i$ 携带 $\delta_i$ 的流量,使得 $\sum \delta_i=\delta$,则
$$
\operatorname{cost}(f_n-f)=\sum_{i=1}^k c(p_i)\delta_i
$$
因为 $c(p_i)\ge c(p)$,所以路径部分的总费用满足:
$$
\sum_{i=1}^k c(p_i)\delta_i\ge \sum_{i=1}^k c(p)\delta_i=c(p)\sum_{i=1}^k \delta_i=c(p)\delta
$$
所以
$$
\operatorname{cost}(f_n-f)\ge c(p)\delta
$$
这就与 $f_n$ 的费用比 $f'$ 的费用小而矛盾,所以这样做是正确的。
在残留网络中,如果正向边的边权为 $w(u,v)$,那么反向边的边权 $w(v,u)$ 定义为 $-w(u,v)$,可以看成退流。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=5010,M=100010,inf=0x3f3f3f3f;
int n,m,S,T;
int h[N],e[M],ne[M],f[M],w[M],idx;
int q[N],d[N],pre[N],incf[N];//d表示从源点到每个点的长度,incf表示走到每个点时的最大流量
bool st[N];
void add(int a,int b,int c,int d){
e[idx]=b;
f[idx]=c;
w[idx]=d;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
w[idx]=-d;
ne[idx]=h[b];
h[b]=idx++;
}
bool spfa(){
int hh=0,tt=1;
mems(d,0x3f);
mems(incf,0);
q[0]=S;
d[S]=0;
incf[S]=inf;
while(hh!=tt){
int t=q[hh++];
if(hh==N) hh=0;//循环队列
st[t]=false;//一个点可以多次入队
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(f[i]>0 && d[ver]>d[t]+w[i]){
d[ver]=d[t]+w[i];
pre[ver]=i;
incf[ver]=min(f[i],incf[t]);
if(!st[ver]){
q[tt++]=ver;
if(tt==N) tt=0;
st[ver]=true;
}
}
}
}
return (incf[T]>0);
}
void EK(int &flow,int &cost){
flow=cost=0;
while(spfa()){
int t=incf[T];//流量
flow+=t;
cost+=t*d[T];
for(int i=T;i!=S;i=e[pre[i]^1]){
f[pre[i]]-=t;
f[pre[i]^1]+=t;
}
}
}
int main(){
cin>>n>>m>>S>>T;
mems(h,-1);
while(m--){
int a,b,c,d;
scanf("%d%d%d%d",&a,&b,&c,&d);
add(a,b,c,d);
}
int flow,cost;
EK(flow,cost);
cout<<flow<<" "<<cost;
return 0;
}
```
## 直接应用
[原题](https://www.acwing.com/problem/content/2194/),[洛谷原题](https://www.luogu.com.cn/problem/P4015)。
建立虚拟源点和汇点,源点向每个仓库连一条容量为 $a_i$,费用为 $0$ 的边;每个商店向汇点连一条容量为 $b_j$,费用为 $0$ 的边。对于运输的路径,连一条容量为 $+\infty$,费用为 $c_{i,j}$ 的边。
对于最优方案,直接求最小费用最大流,对于最差方案,求最大费用最大流。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=160,M=5150*2+10,inf=0x3f3f3f3f;
int n,m,S,T;
int h[N],e[M],ne[M],f[M],w[M],idx;
int q[N],d[N],pre[N],incf[N];
bool st[N];
void add(int a,int b,int c,int d){
e[idx]=b;
f[idx]=c;
w[idx]=d;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
w[idx]=-d;
ne[idx]=h[b];
h[b]=idx++;
}
bool spfa(){
int hh=0,tt=1;
mems(d,0x3f);
mems(incf,0);
q[0]=S;
d[S]=0;
incf[S]=inf;
while(hh!=tt){
int t=q[hh++];
if(hh==N) hh=0;
st[t]=false;
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(f[i]>0 && d[ver]>d[t]+w[i]){
d[ver]=d[t]+w[i];
pre[ver]=i;
incf[ver]=min(incf[t],f[i]);
if(!st[ver]){
st[ver]=true;
q[tt++]=ver;
if(tt==N) tt=0;
}
}
}
}
return (incf[T]>0);
}
int EK(){
int cost=0;
while(spfa()){
int t=incf[T];
cost+=t*d[T];
for(int i=T;i!=S;i=e[pre[i]^1]){
f[pre[i]]-=t;
f[pre[i]^1]+=t;
}
}
return cost;
}
int main(){
cin>>m>>n;
S=0;
T=n+m+1;
mems(h,-1);
for(int i=1;i<=m;i++){
int a;
scanf("%d",&a);
add(S,i,a,0);
}
for(int i=1;i<=n;i++){
int b;
scanf("%d",&b);
add(i+m,T,b,0);
}
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++){
int c;
scanf("%d",&c);
add(i,j+m,inf,c);
}
cout<<EK()<<endl;
for(int i=0;i<idx;i+=2){
f[i]+=f[i^1];
f[i^1]=0;
w[i]=-w[i];//将每条边的费用取反,那么求出来的最小费用最大流就是原先最大的
w[i^1]=-w[i^1];
}
cout<<-EK();//注意这里也要取反
return 0;
}
```
---
[原题](https://www.acwing.com/problem/content/2196/),[洛谷原题](https://www.luogu.com.cn/problem/P4016)。
设分配后每个仓库有 $\overline{x}$ 个货物,则可以将所有点分为两类:
$$
\begin{cases}
a_i>\overline{x}\\
a_i\le\overline{x}\\
\end{cases}
$$
那么我们可以类比上一题,将第一类点放到左边,将第二类点放到右边,源点向左边的点连一条容量为 $a_i-\overline{x}$,费用为 $0$ 的边;右边的点向汇点连一条容量为 $\overline{x}-a_i$,费用为 $0$ 的边。每个点向原环中相邻的两个点连一条容量为 $+\infty$,费用为 $1$ 的边(这里**不保证**两个点一个在左边,一个在右边)。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=110,M=610,inf=0x3f3f3f3f;
int n,S,T;
int s[N];
int h[N],e[M],ne[M],f[M],w[M],idx;
int q[N],d[N],pre[N],incf[N];
bool st[N];
void add(int a,int b,int c,int d){
e[idx]=b;
f[idx]=c;
w[idx]=d;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
w[idx]=-d;
ne[idx]=h[b];
h[b]=idx++;
}
bool spfa(){
int hh=0,tt=1;
mems(d,0x3f);
mems(incf,0);
q[0]=S;
d[S]=0;
incf[S]=inf;
while(hh!=tt){
int t=q[hh++];
st[t]=false;
if(hh==N) hh=0;
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(f[i]>0 && d[ver]>d[t]+w[i]){
d[ver]=d[t]+w[i];
pre[ver]=i;
incf[ver]=min(incf[t],f[i]);
if(!st[ver]){
st[ver]=true;
q[tt++]=ver;
if(tt==N) tt=0;
}
}
}
}
return (incf[T]>0);
}
int EK(){
int cost=0;
while(spfa()){
int t=incf[T];
cost+=d[T]*t;
for(int i=T;i!=S;i=e[pre[i]^1]){
f[pre[i]]-=t;
f[pre[i]^1]+=t;
}
}
return cost;
}
int main(){
cin>>n;
S=0;
T=n+1;
mems(h,-1);
int tot=0;
for(int i=1;i<=n;i++){
scanf("%d",&s[i]);
tot+=s[i];
add(i,(i<n ? i+1 : 1),inf,1);
add(i,(i>1 ? i-1 : n),inf,1);
}
tot/=n;
for(int i=1;i<=n;i++){
if(tot<s[i]) add(S,i,s[i]-tot,0);
else add(i,T,tot-s[i],0);
}
cout<<EK();
return 0;
}
```
## 二分图最优匹配
[原题](https://www.acwing.com/problem/content/2195/),[洛谷原题](https://www.luogu.com.cn/problem/P4014)。
在这类问题中,每条边都会有一个边权,最优匹配指在最大匹配的基础上,边权和最大(最小)的匹配方案。
类比二分图最大匹配的建图方式,只不过中间的边添加费用,费用为 $c_{i,j}$,其他的边的费用为 $0$。
这题建图后,直接求最大费用最大流和最小费用最大流即可。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=110,M=114514,inf=0x3f3f3f3f;
int n,S,T;
int s[N];
int h[N],e[M],ne[M],f[M],w[M],idx;
int q[N],d[N],pre[N],incf[N];
bool st[N];
void add(int a,int b,int c,int d){
e[idx]=b;
f[idx]=c;
w[idx]=d;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
w[idx]=-d;
ne[idx]=h[b];
h[b]=idx++;
}
bool spfa(){
int hh=0,tt=1;
mems(d,0x3f);
mems(incf,0);
q[0]=S;
d[S]=0;
incf[S]=inf;
while(hh!=tt){
int t=q[hh++];
st[t]=false;
if(hh==N) hh=0;
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(f[i]>0 && d[ver]>d[t]+w[i]){
d[ver]=d[t]+w[i];
pre[ver]=i;
incf[ver]=min(incf[t],f[i]);
if(!st[ver]){
st[ver]=true;
q[tt++]=ver;
if(tt==N) tt=0;
}
}
}
}
return (incf[T]>0);
}
int EK(){
int cost=0;
while(spfa()){
int t=incf[T];
cost+=d[T]*t;
for(int i=T;i!=S;i=e[pre[i]^1]){
f[pre[i]]-=t;
f[pre[i]^1]+=t;
}
}
return cost;
}
int main(){
cin>>n;
S=0;
T=n*2+1;
mems(h,-1);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
int a;
scanf("%d",&a);
add(i,j+n,1,a);
}
for(int i=1;i<=n;i++){
add(S,i,1,0);
add(i+n,T,1,0);
}
cout<<EK()<<endl;
for(int i=0;i<idx;i+=2){
f[i]+=f[i^1];
f[i^1]=0;
w[i]=-w[i];
w[i^1]=-w[i^1];
}
cout<<-EK();
return 0;
}
```
## 最大权不相交路径
[原题](https://www.acwing.com/problem/content/2193/),[洛谷原题](https://www.luogu.com.cn/problem/P4013)。
第一问:每个点向左下、右下的点连一条容量为 $1$,费用为 $0$ 的边,因为每个点只能走一次,所以将每个点拆成入点和出点,之间连一条容量为 $1$,费用为这个数字的边。源点向最上面的点连一条容量为 $1$,费用为 $0$ 的边,最下面的点向汇点连一条容量为 $+\infty$,费用为 $0$ 的边。
第二问:将拆点边的容量改成 $+\infty$。
第三问:将左下、右下边的容量也改成 $+\infty$。
直接求最大费用最大流即可。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=1210,M=4010,inf=0x3f3f3f3f;
int n,m,S,T;
int h[N],e[M],ne[M],f[M],w[M],idx;
int q[N],d[N],pre[N],incf[N];
bool st[N];
int id[40][40],cost[40][40];
void add(int a,int b,int c,int d){
e[idx]=b;
f[idx]=c;
w[idx]=d;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
w[idx]=-d;
ne[idx]=h[b];
h[b]=idx++;
}
bool spfa(){
int hh=0,tt=1;
mems(incf,0);
mems(d,-0x3f);
q[0]=S;
d[S]=0;
incf[S]=inf;
while(hh!=tt){
int t=q[hh++];
if(hh==N) hh=0;
st[t]=false;
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(f[i]>0 && d[ver]<d[t]+w[i]){
d[ver]=d[t]+w[i];
pre[ver]=i;
incf[ver]=min(incf[t],f[i]);
if(!st[ver]){
st[ver]=true;
q[tt++]=ver;
if(tt==N) tt=0;
}
}
}
}
return (incf[T]>0);
}
int EK(){
int cost=0;
while(spfa()){
int t=incf[T];
cost+=t*d[T];
for(int i=T;i!=S;i=e[pre[i]^1]){
f[pre[i]]-=t;
f[pre[i]^1]+=t;
}
}
return cost;
}
int main(){
int cnt=0;
cin>>m>>n;
S=++cnt;
T=++cnt;
for(int i=1;i<=n;i++)
for(int j=1;j<=m+i-1;j++){
scanf("%d",&cost[i][j]);
id[i][j]=++cnt;//编号
}
//第一问
mems(h,-1);
idx=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m+i-1;j++){
add(id[i][j]*2,id[i][j]*2+1,1,cost[i][j]);
if(i==1) add(S,id[i][j]*2,1,0);
if(i==n) add(id[i][j]*2+1,T,inf,0);// *2表示入点,*2+1表示出点
if(i<n){
add(id[i][j]*2+1,id[i+1][j]*2,1,0);
add(id[i][j]*2+1,id[i+1][j+1]*2,1,0);
}
}
cout<<EK()<<endl;
//第二问
mems(h,-1);
idx=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m+i-1;j++){
add(id[i][j]*2,id[i][j]*2+1,inf,cost[i][j]);
if(i==1) add(S,id[i][j]*2,1,0);
if(i==n) add(id[i][j]*2+1,T,inf,0);
if(i<n){
add(id[i][j]*2+1,id[i+1][j]*2,1,0);
add(id[i][j]*2+1,id[i+1][j+1]*2,1,0);
}
}
cout<<EK()<<endl;
//第三问
mems(h,-1);
idx=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m+i-1;j++){
add(id[i][j]*2,id[i][j]*2+1,inf,cost[i][j]);
if(i==1) add(S,id[i][j]*2,1,0);
if(i==n) add(id[i][j]*2+1,T,inf,0);
if(i<n){
add(id[i][j]*2+1,id[i+1][j]*2,inf,0);
add(id[i][j]*2+1,id[i+1][j+1]*2,inf,0);
}
}
cout<<EK()<<endl;
return 0;
}
```
## 网格图模型
[原题](https://www.acwing.com/problem/content/384/),[洛谷原题](https://www.luogu.com.cn/problem/P2045)。
我们可以这样建图:
其中源点连向左上角的边和右下角连向汇点的边的容量为 $k$,每个点向下面的点和右面的点连边,这样就可以把原问题的路径转化为可行流。
考虑到原问题的费用在点上,所以我们进行拆点,入点向出点连一条费用为 $w_{i,j}$,容量为 $1$ 的边,但是如果单纯是这样的话,这个点只能走一次,而原问题是:可以走很多次,但是只有一次能累加费用,所以我们再从入点向出点连一条容量为 $+\infty$,费用为 $0$ 的边。然后直接求最大费用最大流。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=50010,M=160010,inf=0x3f3f3f3f;
int n,k,S,T;
int h[N],e[M],ne[M],f[M],w[M],idx;
int q[N],d[N],pre[N],incf[N];
bool st[N];
int get(int x,int y,int t){//t表示是否为入点
return (x*n+y)*2+t;
}
void add(int a,int b,int c,int d){
e[idx]=b;
f[idx]=c;
ne[idx]=h[a];
w[idx]=d;
h[a]=idx++;
e[idx]=a;
f[idx]=0;
ne[idx]=h[b];
w[idx]=-d;
h[b]=idx++;
}
bool spfa(){
int hh=0,tt=1;
mems(d,-0x3f);
mems(incf,0);
q[0]=S;
d[S]=0;
incf[S]=inf;
while(hh!=tt){
int t=q[hh++];
st[t]=false;
if(hh==N) hh=0;
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(f[i]>0 && d[ver]<d[t]+w[i]){
d[ver]=d[t]+w[i];
pre[ver]=i;
incf[ver]=min(f[i],incf[t]);
if(!st[ver]){
st[ver]=true;
q[tt++]=ver;
if(tt==N) tt=0;
}
}
}
}
return (incf[T]>0);
}
int EK(){
int cost=0;
while(spfa()){
int t=incf[T];
cost+=t*d[T];
for(int i=T;i!=S;i=e[pre[i]^1]){
f[pre[i]]-=t;
f[pre[i]^1]+=t;
}
}
return cost;
}
int main(){
cin>>n>>k;
S=2*n*n;
T=S+1;
mems(h,-1);
add(S,get(0,0,0),k,0);
add(get(n-1,n-1,1),T,k,0);
for(int i=0;i<n;i++)
for(int j=0;j<n;j++){
int c;
scanf("%d",&c);
add(get(i,j,0),get(i,j,1),1,c);
add(get(i,j,0),get(i,j,1),inf,0);
if(i+1<n) add(get(i,j,1),get(i+1,j,0),inf,0);
if(j+1<n) add(get(i,j,1),get(i,j+1,0),inf,0);
}
cout<<EK();
return 0;
}
```
---
[原题](https://www.acwing.com/problem/content/2197/),[洛谷原题](https://www.luogu.com.cn/problem/P4012)。
~~浪费了我五分钟读题时间。~~
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=1145,M=114514,inf=0x3f3f3f3f;
int a,b;
int n,m,S,T;
int h[N],e[M],ne[M],f[M],w[M],idx;
int q[N],d[N],pre[N],incf[N];
bool st[N];
int get(int x,int y){
return x*(m+1)+y;
}
void add(int a,int b,int c,int d){
e[idx]=b;
f[idx]=c;
w[idx]=d;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
w[idx]=-d;
ne[idx]=h[b];
h[b]=idx++;
}
bool spfa(){
int hh=0,tt=1;
mems(d,-0x3f);
mems(incf,0);
q[0]=S;
d[S]=0;
incf[S]=inf;
while(hh!=tt){
int t=q[hh++];
if(hh==N) hh=0;
st[t]=false;
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(f[i]>0 && d[ver]<d[t]+w[i]){
d[ver]=d[t]+w[i];
pre[ver]=i;
incf[ver]=min(incf[t],f[i]);
if(!st[ver]){
q[tt++]=ver;
st[ver]=true;
if(tt==N) tt=0;
}
}
}
}
return (incf[T]>0);
}
int EK(){
int cost=0;
while(spfa()){
int t=incf[T];
cost+=t*d[T];
for(int i=T;i!=S;i=e[pre[i]^1]){
f[pre[i]]-=t;
f[pre[i]^1]+=t;
}
}
return cost;
}
int main(){
cin>>a>>b>>n>>m;
S=(n+1)*(m+1);
T=S+1;
mems(h,-1);
for(int i=0;i<n+1;i++)
for(int j=0;j<m;j++){
int c;
scanf("%d",&c);
add(get(i,j),get(i,j+1),1,c);
add(get(i,j),get(i,j+1),inf,0);
}
for(int i=0;i<m+1;i++)
for(int j=0;j<n;j++){
int c;
scanf("%d",&c);
add(get(j,i),get(j+1,i),1,c);
add(get(j,i),get(j+1,i),inf,0);
}
while(a--){
int k,x,y;
scanf("%d%d%d",&k,&x,&y);
add(S,get(x,y),k,0);
}
while(b--){
int r,x,y;
scanf("%d%d%d",&r,&x,&y);
add(get(x,y),T,r,0);
}
cout<<EK();
return 0;
}
```
---
## 拆点
[原题](https://www.acwing.com/problem/content/2186/),[洛谷改输入题](https://www.luogu.com.cn/problem/P1251)。
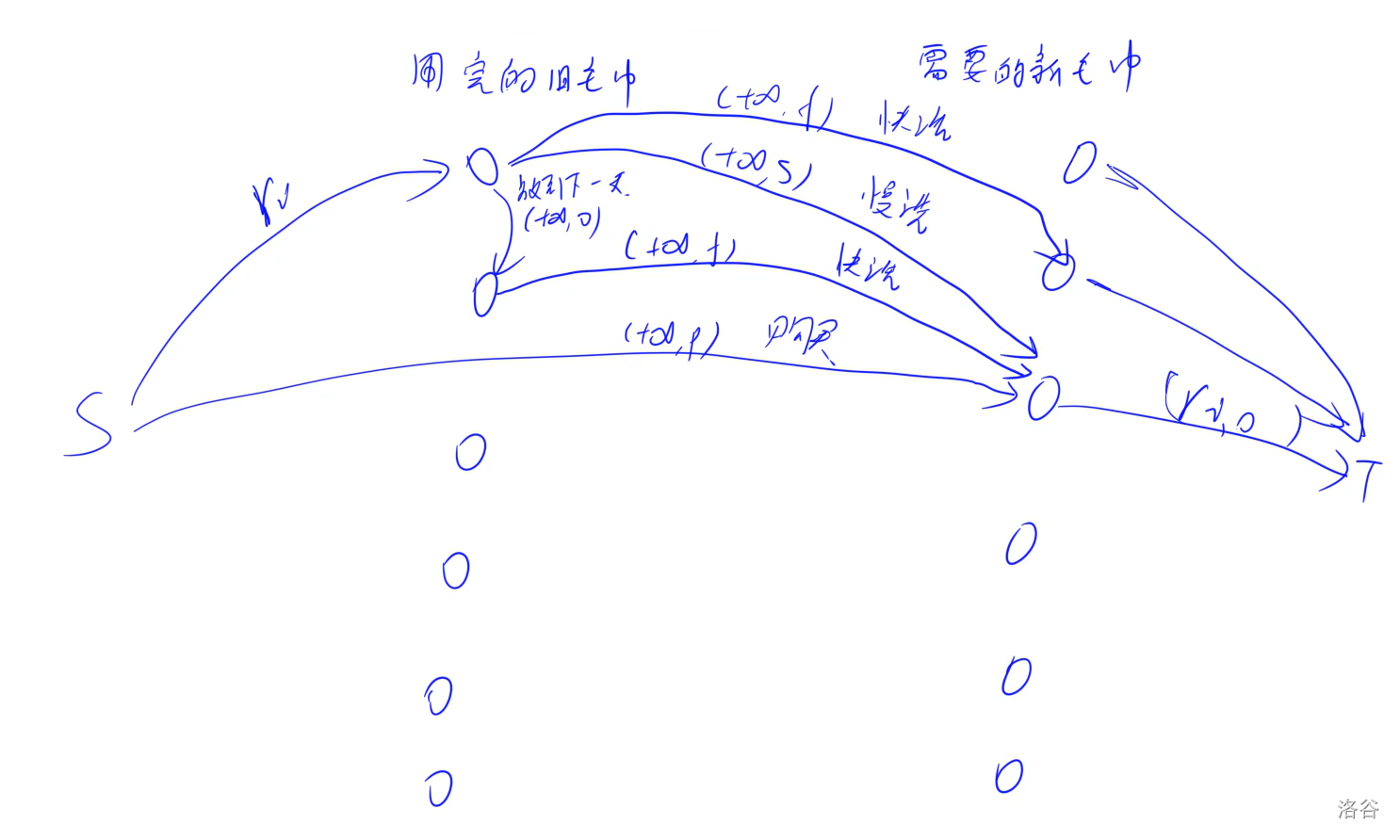
原问题的方案可以与上图的**最大流**相对应,直接求最小费用最大流即可。
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=1610,M=10010,inf=0x3f3f3f3f;
int n,p,x,xp,y,yp,S,T;
int h[N],e[M],ne[M],f[M],w[M],idx;
int q[N],d[N],pre[N],incf[N];
bool st[N];
void add(int a,int b,int c,int d){
e[idx]=b;
f[idx]=c;
w[idx]=d;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
w[idx]=-d;
ne[idx]=h[b];
h[b]=idx++;
}
bool spfa(){
int hh=0,tt=1;
mems(incf,0);
mems(d,0x3f);
q[0]=S;
d[S]=0;
incf[S]=inf;
while(hh!=tt){
int t=q[hh++];
if(hh==N) hh=0;
st[t]=false;
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(f[i]>0 && d[ver]>d[t]+w[i]){
d[ver]=d[t]+w[i];
pre[ver]=i;
incf[ver]=min(incf[t],f[i]);
if(!st[ver]){
st[ver]=true;
q[tt++]=ver;
if(tt==N) tt=0;
}
}
}
}
return (incf[T]>0);
}
int EK(){
int cost=0;
while(spfa()){
int t=incf[T];
cost+=t*d[T];
for(int i=T;i!=S;i=e[pre[i]^1]){
f[pre[i]]-=t;
f[pre[i]^1]+=t;
}
}
return cost;
}
int main(){
cin>>n>>p>>x>>xp>>y>>yp;
S=0;
T=2*n+1;
mems(h,-1);
for(int i=1;i<=n;i++){
int r;
scanf("%d",&r);
add(S,i,r,0);
add(n+i,T,r,0);
add(S,n+i,inf,p);//购买
if(i<n) add(i,i+1,inf,0);//拖延
if(i+x<=n) add(i,i+x+n,inf,xp);//快洗
if(i+y<=n) add(i,n+i+y,inf,yp);//慢洗
}
cout<<EK();
return 0;
}
```
## 上下界可行流
[原题](https://www.acwing.com/problem/content/971/),[洛谷原题](https://www.luogu.com.cn/problem/P3980)。
我们从点 $i$ 向点 $i+1$ 连边,表示第 $i$ 天志愿者的人数,而且每一条都至少要有 $A_i$ 个人,所以这就是一个**无源汇上下界最小费用可行流**。
如果一个志愿者能从第 $S_i$ 天工作到第 $T_i$ 天,就让第 $S_i$ 条边到第 $T_i$ 条边流 $1$ 的流量。但是我们要保证流量守恒,所以从第 $T_i+1$ 个点向第 $S_i$ 个点连一条容量为 $+\infty$,费用为 $C_i$,下界为 $0$ 的边,让这个流量流回去,那么这条边的流量就等于这类志愿者使用了多少人。其他边的容量为 $+\infty$,费用为 $0$,下界为 $A_i$。
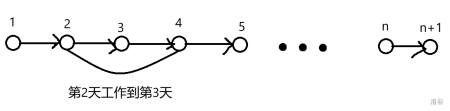
参考代码:
```cpp
#include<bits/stdc++.h>
#define mems(a,b) memset(a,b,sizeof a)
using namespace std;
const int N=10010,M=220010,inf=0x3f3f3f3f;
int n,m,S,T;
int h[N],e[M],ne[M],f[M],w[M],idx;
int q[N],d[N],pre[N],incf[N];
bool st[N];
void add(int a,int b,int c,int d){
e[idx]=b;
f[idx]=c;
w[idx]=d;
ne[idx]=h[a];
h[a]=idx++;
e[idx]=a;
f[idx]=0;
w[idx]=-d;
ne[idx]=h[b];
h[b]=idx++;
}
bool spfa(){
int hh=0,tt=1;
mems(incf,0);
mems(d,0x3f);
incf[S]=inf;
d[S]=0;
q[0]=S;
while(hh!=tt){
int t=q[hh++];
if(hh==N) hh=0;
st[t]=false;
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(f[i]>0 && d[ver]>d[t]+w[i]){
d[ver]=d[t]+w[i];
pre[ver]=i;
incf[ver]=min(incf[t],f[i]);
if(!st[ver]){
st[ver]=true;
q[tt++]=ver;
if(tt==N) tt=0;
}
}
}
}
return (incf[T]>0);
}
int EK(){
int cost=0;
while(spfa()){
int t=incf[T];
cost+=t*d[T];
for(int i=T;i!=S;i=e[pre[i]^1]){
f[pre[i]]-=t;
f[pre[i]^1]+=t;
}
}
return cost;
}
int main(){
cin>>n>>m;
S=0;
T=n+2;
mems(h,-1);
int last=0;//前一天的人数,相当于C入
for(int i=1;i<=n;i++){
int cur;
scanf("%d",&cur);
if(last>cur) add(S,i,last-cur,0);
else add(i,T,cur-last,0);
add(i,i+1,inf,0);
last=cur;
}
add(S,n+1,last,0);
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(b+1,a,inf,c);
}
cout<<EK();
return 0;
}
```
# 后记
非常感谢你能看到这里!
整理自:[AcWing算法进阶课](https://www.acwing.com/activity/content/32/)。